Гибка фасонных элементов: Гибка фасонных элементов в СПб

Гибка фасонных элементов в СПб

• Производитель сэндвич-панелей
• Услуги
• Гибка фасонных элементов

Обработка металла часто связана с операциями по пластическому деформированию – гибкой элементов. Она представляет собой промышленный процесс, при котором листовой металл получает требуемую форму. Заготовка формируется механическим способом с использованием специальных приспособлений. При гибке металлических элементов растягиваются наружные слои и одновременно сжимаются внутренние, в результате чего одна часть заготовки перегибается под определенным углом по отношению к другой.

Основные направления ООО «Метпан»

Мы выполняем гибку фасонных и доборных элементов с защитным полимерным покрытием:

• стальные уголки с оцинковкой;
• фаски различной формы;
• соединительные планки;
• нащельники разных конфигураций;
• наружные откосы для оконных проемов;
• отливы;
• планки примыканий;
• ендова и накладки;
• ветровые и торцевые стальные планки;
• карнизы.

Изготовление фасонных элементов

Гибка фасонных элементов в СПб – одно из главных направлений компании. У нас можно заказать оперативное изготовление фасонных изделий для сэндвич-панелей из оцинкованной стали. Цвета подбираются в соответствии с палитрой RAL, что позволяет выбрать изделия под общий стиль строения.

Мы ценим наших клиентов и гарантируем:

• прозрачные расчеты, отсутствие скрытых доплат;
• европейское качество;
• точное соблюдение сроков и обязательств, прописанных в договоре;
• оперативную доставку товаров.

Цена на гибку элементов из металлов зависит от объема работ, размера заготовок, срочности реализации проекта. Для предварительного расчета стоимости можно связаться с нашими менеджерами.

Примеры наших работ по гибке элементов

Схема работы с нами

1. Заявка

Оставьте заявку на изготовление на сайте, в чате или позвоните нам +7(812) 438-09-87.

2. Производство

В нашем цехе можно изготовить до 200 изделий за смену.

3. Доставка

Доставляем заказы в Санкт-Петербурге и по всей России.

Расчет стоимости материалов для объекта

Заказать

Технология гибки элементов

Для гибки фасонных элементов мы используем специализированные гибочные штампы. Лист размещается и надежно закрепляется в прессе с последующим сгибанием. Несмотря на относительно простую технологию с ее помощью удается производить детали различного вида и толщины. Изделия, полученные на листогибочных прессах, имеют эстетичный вид и длительный срок годности, поскольку являются цельными.

Преимущества гибки металлов

В отличие от других методов обработки металла (сварки, резки), гибка имеет следующие преимущества:

• экономичность – при работе практически полностью отсутствуют отходы;
• механическая прочность – за счет отсутствия сварных швов и соединений;
• точность обработки – на современном оборудовании можно получить детали очень сложной конфигурации;
• коррозионная стойкость – в месте гибки фасонных изделий практически не происходит изменение структуры металла.

Другие услуги

Раскладка сэндвич-панелей

Упаковка сэндвич-панелей

Гибка любых фасонных изделий, компания “Альянс Профиль”

Главная → Гибка фасонных изделий

Компания “Альянс Профиль” предлагает изготовление любых элементов по эскизам заказчиков из стали толщиной от 0,35 до 2 мм. Гибка листового металла производится с целью придания изделию необходимой конфигурации. Во время гибки внутренние слои металла сжимаются, а наружные растягиваются, и при этом сохраняется прочность и антикоррозийные свойства материала. Гибка металла с соблюдением технологии позволяет производить из листов стали различные профили и изделия сложных геометрических форм, обладающие высокими качественными характеристиками.

Виды фасонных изделий:

Существует великое множество фасонных изделий, каждое из которых спроектировано для выполнения определенной функции. Мы приведем перечень основных фасонных изделий, которые наша компания предлагает своим клиентам.

Оконные отливы и цокольные отливы

Мы осуществляем гибку оконных отливов (верхних и подоконных), цокольных отливов необходимых для отведения воды от фундамента, а также наличников, выполняющих в сочетании с отливами декоративные функции и придающих окну завершенный вид.

               

Доборные элементы кровли

Мы изготовляем весь ассортимент планок для обустройства кровли: планки ендовы для отвода воды, карнизные планки для защиты лобовой доски карниза от осадков, торцевые планки (фронтоны) для защиты кровельного пирога от влаги и ветра, планки примыкания для герметизации примыканий, а также коньки различной формы для защиты вентиляционного зазора от попадания влаги. Мы также осуществляем гибку снегостопоров (снегозадержателей), являющихся немаловажными элементами безопасности кровли в условиях северного климата.

 

Парапетный отлив

Как известно, парапет – это ограждение на крыше здания, террасе, балконе или мосте, которое служит для защиты жизни людей, находящихся на ограждаемых объектах. Однако, парапеты и сами нуждаются в защите от разрушения. В ассортимент изготавливаемой нами продукции входят парапетные крышки различной формы, которые позволяют защитить ограждающие конструкции от воздействия атмосферных осадков.

         

Колпак на трубу дымохода (флюгарка)

Негативное воздействие окружающей среды заставляет проектировщиков создавать защитные конструкции для всех уязвимых мест дома. Жизненно необходимым защитным элементом для трубы здания является флюгарка. Флюгарки предотвращают попадание влаги внутрь трубы, препятствуя тем самым ее отсыреванию и разрушению. Флюгарки также устанавливаются на вентиляционных выводах и на газоходах. Мы изготавливаем флюгарки любого назначения и размера.

         

Колпак на заборный столб

В защите от влаги нуждаются не только части дома, но и компоненты забора. Мы предлагаем своим клиентам колпаки на заборные столбы, выполняющие как защитные, так и декоративные функции. Нижняя часть колпака надежно закрывает верхнюю кладку столба, а верхняя часть колпака благодаря специально сконструированной юбке отводит воду от остальной длины столба.

В зависимости от дизайнерских требований колпаки, флюгарки, парапетные крышки (накрывные планки), планки обустройства кровли, оконные отливы и наличники могут быть выполнены в любом из цветов таблицы RAL.

         

Фасонные элементы для сэндвич панелей

Относительно недавно в мире строительства появился такой материал, как сэндвич-панели. За период около 30-ти лет данный материал получил широкое распространение в России. Основными его преимуществами являются легкость монтажа и дешевизна создаваемых конструкций. В современных условиях всё чаще необходимо строительство быстровозводимых домов. Поэтому сэндвич-панели, состоящие из двух стальных профилированных листов, между которыми находится слой утеплителя, приобрели большую популярность. При строительстве быстровозводимых зданий помимо сэндвич-панелей требуются и различные фасонные элементы: внутренние и наружные углы, нащельники для сэндвич-панелей, отливы, планки парапета, коньковые элементы и пр. Данные фасонные элементы необходимы для защиты узлов соединения панелей и стыков от воздействия окружающей среды, а также для придания зданию эстетичного вида.

Мы предлагаем изготовление любых фасонных элементов для сэндвич-панелей по Вашим чертежам и размерам.

            

Все изделия могут быть выполнены из оцинкованной стали с полиэстеровым покрытием в любом из цветов таблицы RAL. При этом максимальная ширина развертки равна 1,25 м, а максимальная длина изделия — 6 м. Мы снабжаем фасонными изделиями как производства, так и частных лиц. Качество гарантировано.

 

[email protected]

(812) 448-03-85   (812) 319-78-82

• Оконный отлив
• Цокольный отлив
• Парапетный отлив
• Фасонные элементы для сэндвич панелей
• Колпак на трубу дымохода (флюгарка)
• Колпак на заборный столб
• Металлические наличники

Механика материалов: изгиб – нормальное напряжение » Механика гибких конструкций

---

исследования

человек

курсы

блог

---

Моменты площади

Чтобы рассчитать напряжение (и, следовательно, деформацию), вызванное изгибом, нам нужно понять, где находится нейтральная ось балки и как рассчитать второй момент площади для данного поперечного сечения.

Начнем с того, что представим себе произвольное поперечное сечение — что-то не круглое, не прямоугольное и т. д. 

На изображении выше произвольная форма имеет площадь, обозначенную A . Мы можем посмотреть на небольшую дифференциальную область

дА , которая существует на расстоянии x и y от начала координат. Мы можем посмотреть на первый момент площади в каждом направлении по следующим формулам:

Первый момент площади — это интеграл длины по площади — это означает, что он будет иметь единицы длины в кубе [L ³ ]. Это важно, потому что помогает нам найти центр тяжести объекта.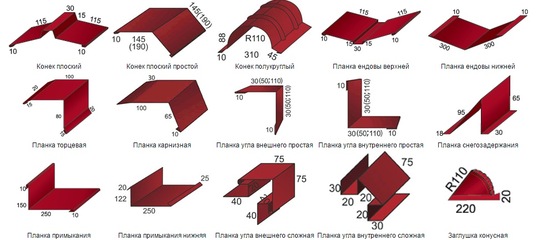 Центроид определяется как “среднее  x (или y ) позиции области”. Математически это утверждение выглядит так:

Крайняя правая часть приведенных выше уравнений будет очень полезна в этом курсе — она позволяет нам разбить сложную фигуру на простые формы с известными площадями и известным расположением центроидов. В большинстве инженерных сооружений есть хотя бы одна ось симметрии — и это позволяет значительно упростить нахождение центроида. Центроид должен располагаться на оси симметрии

. Например: 

Для поперечного сечения слева мы знаем, что центроид должен лежать на оси симметрии, поэтому нам нужно найти только центроид вдоль оси y . Поперечное сечение справа еще проще — поскольку центроид должен совпадать с осями симметрии, он должен быть в центре объекта.

Теперь, когда мы знаем, как найти центр тяжести, мы можем обратить внимание на второй момент площади. Как вы, возможно, помните из предыдущего раздела о кручении, это определяется как:

И, наконец, иногда нам нужно будет определить второй момент площади относительно произвольной оси x или y , которая не соответствует центроиду. В этом случае мы можем использовать теорему о параллельных осях для его вычисления. В этом случае мы используем второй момент площади относительно центроида плюс термин, который включает расстояния между двумя осями.

Это уравнение называется теоремой о параллельных осях . Это будет очень полезно на протяжении всего курса. Как описано во вступительном видео к этому разделу, вычисление второго момента площади простой формы может быть простым. Для более сложных форм нам потребуется вычислить I путем вычисления отдельных I для каждой простой формы и объединения их вместе с использованием теоремы о параллельных осях.

Диаграммы сдвига и момента

Поперечная нагрузка относится к силам, которые перпендикулярны длинной оси конструкции. Эти поперечных нагрузок вызовут изгибающий момент M  , который вызывает нормальное напряжение , и поперечную силу  V , которая вызывает касательное напряжение

. Эти силы могут и будут варьироваться по длине балки, и мы будем использовать диаграммы сдвига и момента (диаграмма VM) для извлечения наиболее подходящих значений. Построение этих диаграмм должно быть вам знакомо по статике , но мы рассмотрим их здесь. При исследовании балки с поперечной нагрузкой необходимо учитывать два важных момента:

1. Как балка нагружена?

• точечная нагрузка, распределенная нагрузка (равномерная или переменная), комбинация нагрузок…

1. Как балка поддерживается?

• свободно опертый, консольный, нависающий, статически неопределимый…

Знание нагрузок и опор позволит вам начертить качественную диаграмму V-M, а затем статический анализ свободного тела поможет вам определить количественное описание кривых. Начнем с того, что вспомним наши

соглашений о знаках .

Эти условные знаки должны быть знакомы. Если сдвиг вызывает вращение против часовой стрелки, он положительный.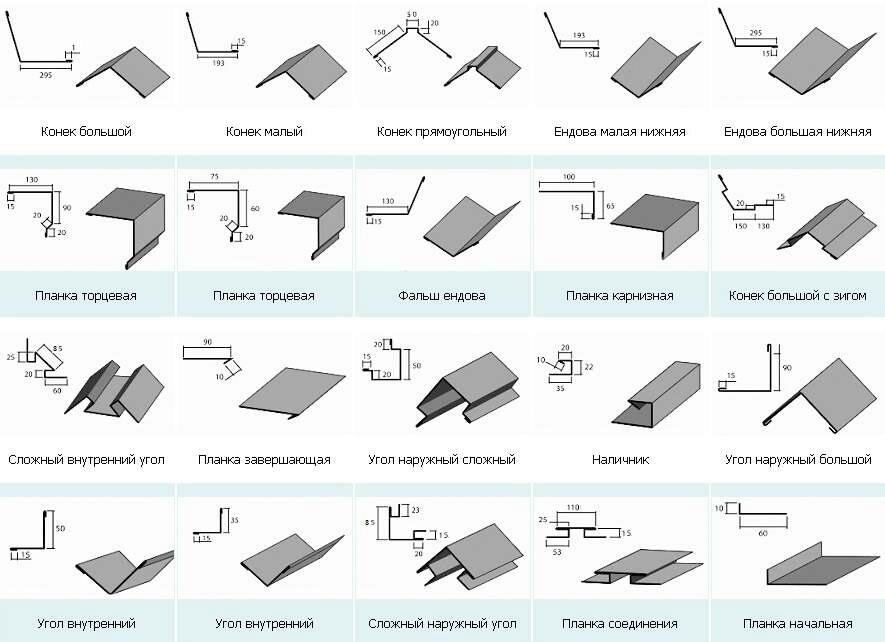 Если момент изгибает луч таким образом, что луч изгибается в «улыбку» или U-образную форму, он положительный. Лучший способ вспомнить эти диаграммы — это проработать пример. Начните с этой консольной балки — отсюда вы можете переходить к более сложным нагрузкам.

Нормальное напряжение при изгибе

Во многом изгиб и кручение очень похожи. Изгиб возникает из-за приложенной пары или изгибающего момента

  M . Как и при кручении, при чистом изгибе в материале есть ось, на которой напряжение и деформация равны нулю. Это называется нейтральной осью . И, как и при кручении, напряжение уже не одинаково по сечению конструкции — оно меняется.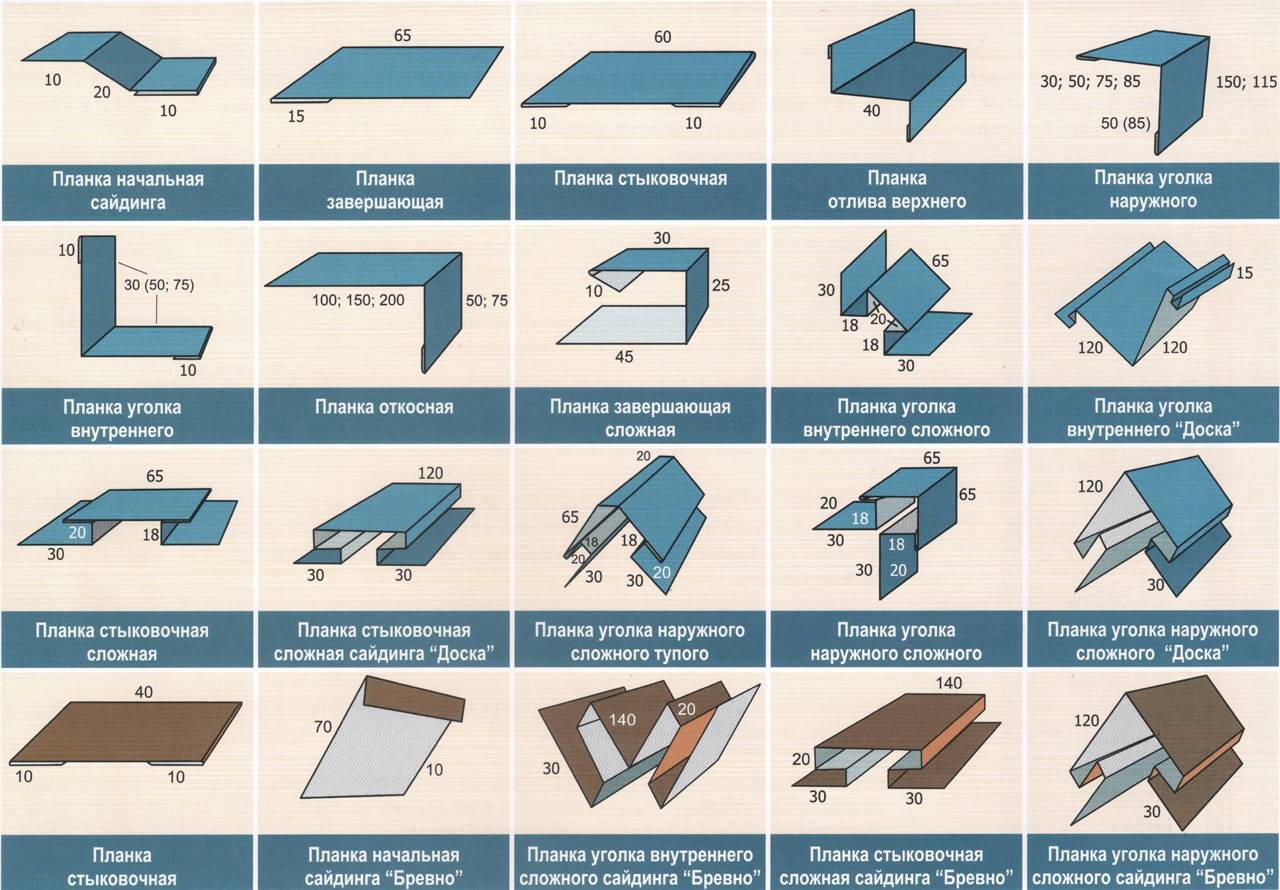 Давайте начнем с того, что рассмотрим момент о z – ось изгибает конструкцию. В данном случае мы не будем ограничиваться круглыми сечениями – на рисунке ниже рассмотрим призматическое сечение.

Прежде чем мы углубимся в математику изгиба, давайте попробуем понять его концептуально. Возможно, лучший способ увидеть, что происходит, — наложить изогнутую балку поверх оригинальной прямой балки.

Теперь вы можете заметить, что нижняя поверхность луча стала длиннее, а верхняя поверхность луча стала короче. Также по центру луча длина вообще не изменилась – соответствует нейтральной оси. Повторяя это язык этого класса, мы можем сказать, что нижняя поверхность находится под напряжением, а верхняя поверхность находится под сжатием. Кое-что, что является немного более тонким, но все еще можно наблюдать из наложенного выше изображения, заключается в том, что смещение луча изменяется линейно сверху вниз, проходя через ноль на нейтральной оси. Помните, это именно то, что мы видели и при кручении — напряжение линейно менялось от центра к центру.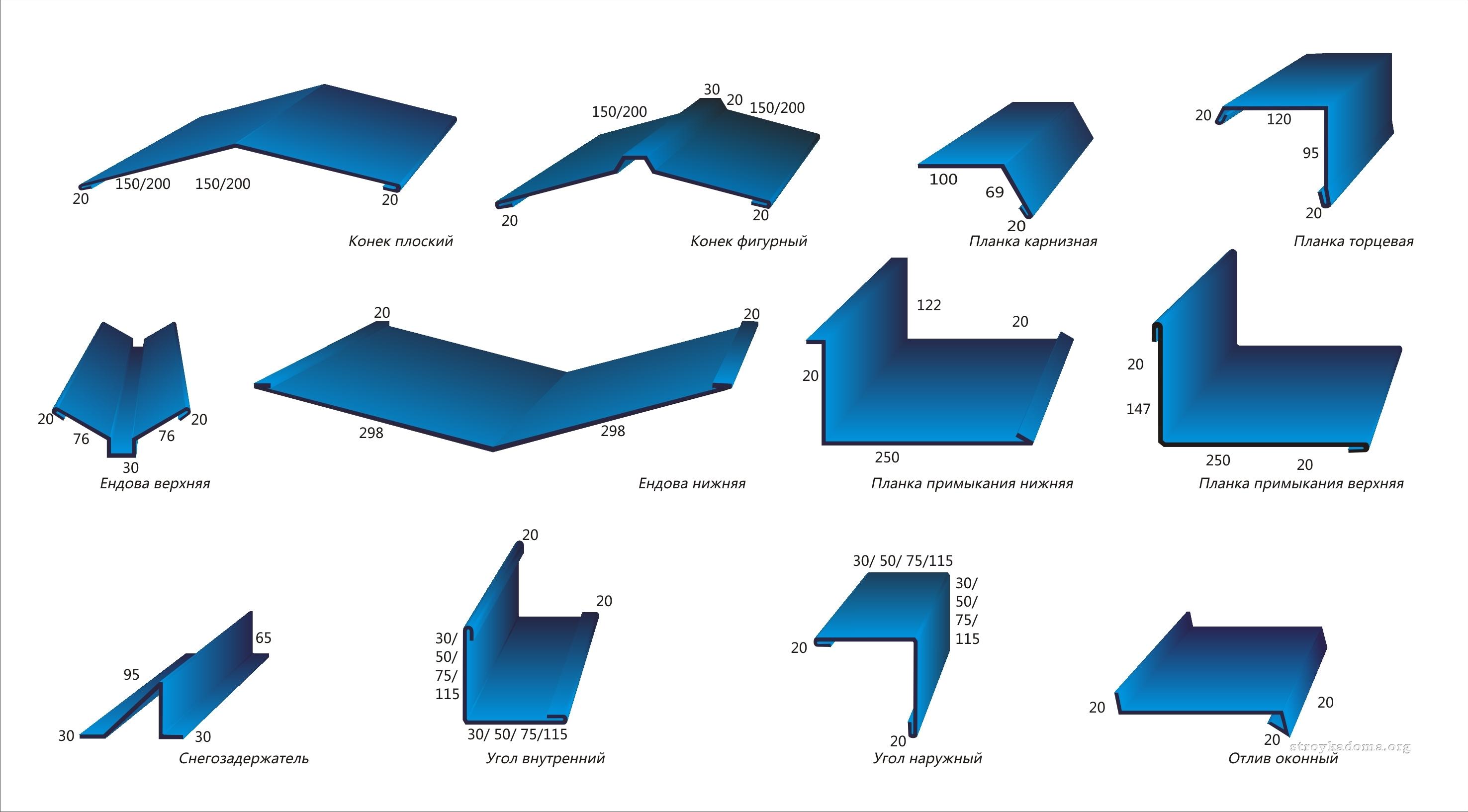

Мы можем посмотреть на это распределение напряжений по поперечному сечению балки немного более явно:

Теперь мы можем найти математическую связь между приложенным моментом и напряжением внутри балки. Мы уже упоминали, что балка деформируется линейно от одного края к другому — это означает, что деформация в направлении x увеличивается линейно с расстоянием вдоль оси y- (или по толщине балки). Таким образом, деформация будет максимальной при растяжении при y = -c (поскольку y=0 находится на нейтральной оси, в данном случае в центре балки), и будет максимальной при сжатии при y=c . Мы можем записать это математически следующим образом:

Теперь это говорит нам кое-что о деформации, что мы можем сказать о максимальных значениях напряжения? Начнем с умножения обеих частей уравнения на E , модуль упругости Юнга. Теперь наше уравнение выглядит так:

Используя закон Гука, мы можем связать эти величины с фигурными скобками под ними с напряжением в направлении x и максимальным напряжением. Что дает нам это уравнение для напряжения в направлении x-:

Наш последний шаг в этом процессе — понять, как изгибающий момент связан с напряжением. Для этого вспомним, что момент — это произведение силы на расстояние. Если мы можем представить себе, что смотрим только на очень маленький элемент в луче, дифференциальный элемент, то мы можем записать это математически как:

Поскольку в нашем уравнении есть дифференциалы, мы можем определить момент M , действующий по площади поперечного сечения балки, путем интегрирования обеих частей уравнения. И если мы вспомним наше определение напряжения как силы на единицу площади, мы можем написать:

 

Последний член в последнем уравнении — интеграл по y в квадрате — представляет второй момент площади относительно оси z (из-за того, как мы определили наши координаты). В декартовых координатах этот второй момент площади обозначается I (в цилиндрических координатах, помните, обозначался J ). Теперь мы можем, наконец, записать наше уравнение для максимального напряжения и, следовательно, напряжения в любой точке вдоль оси y , как:

 

Важно отметить, что нижние индексы в этом уравнении и направление вдоль поперечного сечения (здесь оно измеряется вдоль y ) будут меняться в зависимости от характера проблемы, то есть направления момента — по какой оси находится луч. сгибаясь? Мы основывали наши обозначения на изображении изогнутой балки на первом изображении этого урока.

Помните, в начале раздела я упомянул, что изгиб и кручение на самом деле очень похожи? На самом деле мы очень ясно видим это в последнем уравнении. В обоих случаях напряжение (нормальное для изгиба и сдвиговое для кручения) равно пар/момент ( M для изгиба и T для кручения), умноженных на положение вдоль поперечного сечения. , , потому что напряжение неравномерно по поперечному сечению  (с декартовыми координатами для изгиба и цилиндрическими координатами для кручения), все делится на второй момент площади поперечного сечения.

Сводка

На этом уроке мы узнали о моментах площади и диаграммах момента сдвига . Из первого момента площади поперечного сечения мы можем вычислить центроид . Мы узнали, как вычислить секундный момент площади в декартовых и полярных координатах, и мы узнали, как теорема о параллельных осях позволяет нам вычислить второй момент площади относительно центра тяжести объекта — это полезно для разбиения сложного поперечного сечения на несколько простых фигур и объединение их вместе. Мы пересмотрели концепцию 9Диаграммы сдвига и момента 0015 из статики. Эти диаграммы будут необходимы для определения максимальной силы сдвига и изгибающего момента вдоль сложно нагруженной балки, что, в свою очередь, потребуется для расчета напряжений и прогнозирования разрушения. Наконец, мы узнали о нормальном напряжении от изгиба балки. И напряжение, и деформация изменяются по поперечному сечению балки, при этом одна поверхность растягивается, а другая сжимается. Плоскость, проходящая через центр тяжести, образует нейтральную ось — вдоль нейтральной оси нет напряжений или деформаций. Напряжение является функцией приложенного момента и второго момента площади относительно оси, вокруг которой находится момент.

Этот материал основан на работе, поддержанной Национальным научным фондом в рамках гранта № 1454153. Любые мнения, выводы и выводы или рекомендации, выраженные в этом материале, принадлежат авторам и не обязательно отражают точку зрения Национальный научный фонд.

О различных элементах КЭ для изгиба балки

В этом посте представлено сравнение между различными составами шестигранных элементов КЭ в задаче чистого изгиба консольной балки. 9Результаты анализа 0215 FEM обрабатываются в программе CAE-Viewer , инструменте iChrome для CAE-моделей и визуализации результатов. Извлеченные результаты затем сравниваются с аналитическим решением с помощью Grapheme , инструмента визуализации и анализа данных iChrome. Анализ
FEM выполняется с помощью бесплатного пакета конструкционных конечных элементов CalculiX.

Содержание

Этот пост организован следующим образом:

1. Геометрия и модель FEM
2. Нагрузка и граничные условия
3. Результаты
4. Выводы

Геометрия и модель МКЭ

Рассматривается стальная консольная балка квадратного сечения. Размеры балки указаны в следующей таблице.

Геометрия луча в CAE-Viewer

Размеры луча

Размер прямоугольного сечения		Длина балки
б (мм)	ч (мм)	Д (мм)
100	100	1500

Использованы шестигранные элементы. Различные сетки были сгенерированы с учетом следующих стратегий уточнения:

• p-уточнение : стратегия, направленная на улучшение результатов за счет повышения точности поля смещения в каждом элементе. Этот метод относится к увеличению степени наибольшего полного многочлена (p) внутри элемента без изменения количества используемых элементов. В обсуждаемом здесь контрольном примере линейные шестигранные элементы ( C3D8 / C3D8I в CalculiX) и квадратичные шестигранные элементы ( C3D20 в CalculiX).
• h-уточнение : стратегия, направленная на улучшение результатов за счет уменьшения размера элемента при сохранении того же состава элемента. Эта стратегия обычно реализуется путем разделения каждого существующего элемента на два или более элементов без изменения исходного соотношения сторон. Для этого теста четыре разных сетки ( A , B , C и D ) были созданы с помощью h-уточнения. Подробная информация о каждой сетке представлена ​​в следующей таблице.

Модели FEM – количество элементов

Сетка	Количество элементов
	б	ч	Длина
А	1	1	15
Б	2	2	30
С	4	4	60
Д	8	8	120

Для анализа МКЭ использовались следующие свойства материала:

Свойства материала МКЭ

Материал	Модуль упругости [МПа]	Коэффициент Пуассона
Конструкционная сталь	210000	0,30

 

Сетка A

Сетка B

Сетка C

Сетка D

Нагрузки и граничные условия

Консоль балка зажата с одного конца и свободна с другого. К свободному концу приложена статическая нагрузка 1000 Н в положительном направлении по оси z.

Статический анализ был выполнен для каждой сетки и для каждого состава элемента.

Аналитическая формулировка

Балка достаточно тонкая, чтобы можно было использовать формулу Эйлеро-Бернулли для оценки сходимости анализа методом конечных элементов. В соответствии с этой формулировкой вертикальное перемещение (w ₀ ) свободной балки может быть выражено как функция положения вдоль оси балки (x):

смещения, а затем может использоваться для оценки нормального напряжения с использованием формулы Навье (действительно только для главных осей). Максимальное нормальное напряжение в сечении можно получить следующим образом:

Результаты

В следующих таблицах представлены результаты, полученные для каждой сетки и для каждого состава элемента. Результаты указаны в виде процентной ошибки по отношению к аналитическому решению.

Результаты анализа методом конечных элементов — элементы C3D8

СЕТКА	Ошибка вертикального смещения на свободном конце (%)	Погрешность напряжения на расстоянии 700 мм от зажатого конца (%)
А	36,78	23,93
Б	13,29	3,13
С	3,97	-1,90
Д	1,21	-1,89

Результаты анализа методом конечных элементов — элементы C3D8I

СЕТКА	Ошибка вертикального смещения на свободном конце (%)	Погрешность напряжения на расстоянии 700 мм от зажатого конца (%)
А	0,73	0,00
Б	0,70	0,00
С	0,42	0,00
Д	0,28	0,00

Результаты анализа методом конечных элементов — элементы C3D20

СЕТКА	Ошибка вертикального смещения на свободном конце (%)	Погрешность напряжения на расстоянии 700 мм от зажатого конца (%)
А	1,30	0,00
Б	0,51	0,00
С	0,30	0,00
Д	0,23	0,00

Как и ожидалось, линейные шестигранные элементы (элементы C3D8) обычно приводят к неверным результатам в распределении напряжения и прогибе свободного конца. Однако погрешность можно уменьшить, увеличив количество элементов вдоль оси луча. Для достижения хорошего уровня точности необходимо использовать не менее четырех элементов по высоте (сетка C). Для задач с преобладанием изгиба расширенные формулы деформации (C3D8I) или квадратичные элементы функций формы (C3D20) дают хорошие результаты даже с одним элементом по высоте.

Восьмиузловой кирпичный элемент несовместимого режима C3D8I является улучшенной версией элемента C3D8. В частности, блокировка при сдвиге удаляется, а объемная блокировка значительно уменьшается по сравнению со стандартным составом. Это достигается путем добавления к стандартным функциям формы так называемых пузырьковых функций, которые имеют нулевое значение во всех узлах и ненулевые значения между ними. Элемент C3D8I следует использовать во всех случаях, когда линейные элементы подвергаются изгибу.

Хотя качество элемента C3D8I намного лучше, чем у элемента C3D8, наилучшие результаты получаются с квадратичными элементами (C3D20).

МКЭ Результаты, визуализированные в CAE-Viewer

На следующих изображениях показаны вертикальное смещение и контур напряжений для каждого решения.

Сравнение различных сеток с элементами C3D8 – Контур вертикального смещения

Сравнение различных сеток с C3D8 элементов — контур нормального напряжения

Сравнение различных сеток с C3D8I элементов — контур вертикального смещения

Сравнение различных сеток с элементами C3D8I — контур нормального напряжения сын между разными сетками с C3D20 элементов – Контур вертикального смещения

Сравнение различных сеток с элементами C3D20 – Контур нормального напряжения

На следующих изображениях сообщается об ошибке вертикального смещения относительно положения вдоль оси луча, созданного в Grapheme.

Элементы C3D8 – Ошибка вертикального смещения в зависимости от положения вдоль оси луча

Элементы C3D8I – Ошибка вертикального смещения в зависимости от положения вдоль оси луча

Элементы C3D20 – Ошибка вертикального смещения в зависимости от положения вдоль оси луча

Заключения

CAE Viewer для постобработки результатов CalculiX чистой задачи на изгиб.