Справочные таблицы коэффициента местного сопротивления
Все мы прекрасно видели в таблице аэродинамического расчета столбик коэффициента местного сопротивления (КМС). Постараемся найти ответы на вопросы: Что это? От каких факторов зависит коэффициент местного сопротивления? Зачем вообще его учитывать? И самый главный вопрос: как определить коэффициенты местных сопротивлений воздуховодов? Значение определяется опытным путем и расчетами. Для стандартных элементов таких как тройник, колено, задвижка, диффузор, решетки и другие уже давно определили коэффициенты местных сопротивлений. Данные со значением коэффициентов можно найти в справочной литературе, или же они указаны в каталоге производителя. Бывают случаи, когда и нужно воспользоваться калькулятором. Ниже вы можете увидеть таблицы коэффициентов из справочников и каталогов, а также рассмотрим расчет коэффициента местных сопротивлений и от чего он зависит.
Содержание статьи:
Коэффициент местного сопротивления
Сначала дадим определение коэффициенту местного сопротивления.
- поворот воздуховода,
- сужение или расширение потока,
- вход воздуха в воздухозаборную шахту;
- «тройник» и «крестовина»;
- приточные и вытяжные решетки и воздухораспределители;
- воздухораспределители;
- диффузор;
- заслонки и т.д.
Их КМС рассчитываются по определенным формулам, а затем они участвуют в определении местных потерь давления. В математическом понятии коэффициент местных потерь — это отношение потерь известного напора в местном сопротивлении к скоростному напору.
Коэффициент местного сопротивления зависит от формы и вида местного сопротивления, шероховатости воздуховода и как ни странно от числа Рейнольдса. Для заслонок и другой запорной арматуры к перечисленному додается еще степень открытия.
Связанность КМС с числом Рейнольдса выражается в формуле
Значения коэффициентов В для некоторых местных сопротивлений
Чем больше число Rе тем меньше от него зависит коэффициент. Полная независимость коэффициента местного сопротивления от числа Rе в вентиляционной системе происходит для резких переходов при Rе > 3000, а для плавных переходов — при Rе > 10000.
Суммарный коэффициент местных сопротивлений на участке воздуховода равен сумме всех местных коэффициентов на этом участке.
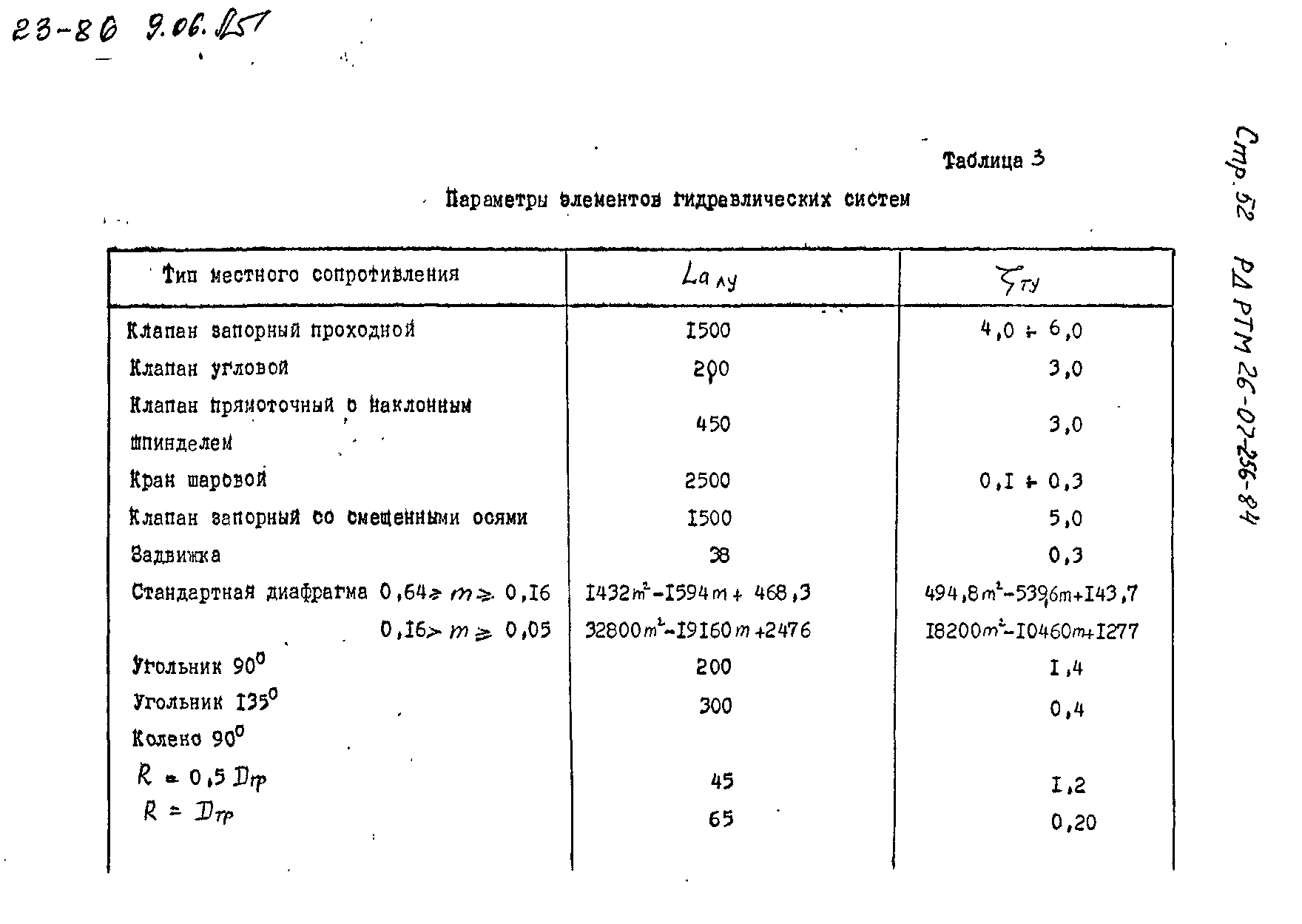Но, конечно, уж если совсем никаких данных не нашли, тогда нужно прибегнуть к математике. Таблица коэффициентов местного сопротивления
Мы проанализировали техническую литературу и другие источники и предоставляем вам для пользования таблицы со значениями КМС для разных элементов системы. В нашем случае это каталоги фирмы ВЕЗА, Belimo, справочник проеткировщика Н,Н, Павлова и справочник Р. В. Щекина.
Значение коэффициента сопротивления для колена, отвода, расширения, сужения, диффузора и конфузора
Таблица коэффициентов местных сопротивлений тройника
Таблица коэффициентов местного сопротивления клапана, задвижки, зонта, решетки
Коэффициент местного сопротивления обратного клапана в зависимости от габаритов
Таблица значения КМС для проточных проемов
Значение коэффициента местного сопротивления противопожарного клапана
Надеемся статья будет вам полезной.
Читайте также:
1 | Задвижка | 0.5 |
2 | Вентиль с косым шпинделем | 0.5 |
3 | Вентиль с вертикальным шпинделем | 6.0 |
4 | Обратный клапан нормальный | 7. |
5 | Обратный клапан «захлопка» | 3.0 |
6 | Кран проходной | 2 |
7 | Компенсатор однолинзовый без рубашки | 1.6- 0.5 |
8 | Компенсатор однолинзовый с рубашкой | 0. |
9 | Компенсатор сальниковый | 0.3 |
10 | 2.8 | |
11 | Отводы, гнутые под углом 90° | – |
12 | со складками R=3d | 0. |
13 | со складками R=4d | 0.5 |
14 | гладкие R=1d | 1.0 |
15 | гладкие R=3d | 0.5 |
16 | гладкие R=4d | 0. |
17 | Отводы сварные одношовные под | – |
18 | углом 30° | 0.2 |
19 | углом 45° | 0.3 |
20 | углом 60° | 0. |
21 | Отводы сварные двухшовные | – |
22 | под углом 90° | 0.6 |
23 | то же, трехшовные | 0.5 |
24 | Тройник при слиянии потока: | – |
25 | проход | 1. |
26 | ответвление | 1.8 |
27 | Тройник при разветвлении потока: | – |
28 | проход | 1.0 |
29 | ответвление | 1. |
30 | Тройник при встречном потоке | 3.0 |
31 | Внезапное расширение | 1.0 |
32 | Внезапное сужение | 0.5 |
33 | Грязевик | 10 |
0
1
8
3
2
5Таблицы коэффициентов местных сопротивлени – Энциклопедия по машиностроению XXL
Таблица коэффициентов местных сопротивлений [c.
528]В таблицах, приводимых ниже, содержатся данные о коэффициентах местного сопротивления, полученных из опытов, для вполне развившейся турбулентности. [c.192]
Значения коэффициента местного сопротивления для задвижки и вентилей зависят от степени открытия последних значения этих коэффициентов даются в таблицах 2 и 3. [c.192]
Таблицы б и 7 содержат значения коэффициентов местного сопротивления для различных деталей трубопроводов, в которых поток претерпевает резкий поворот на определенный угол (тройники, колена, дроссельные и шарнирные клапаны и пробковые краны). [c.194]
Данные таблицы 8 иллюстрируют значения коэффициентов местного сопротивления для разновидностей резкого изменения поперечного сечения потока. [c.196]
Пользуясь таблицами значений коэффициентов местных сопротивлений, определить, насколько следует прикрыть задвижку
[c.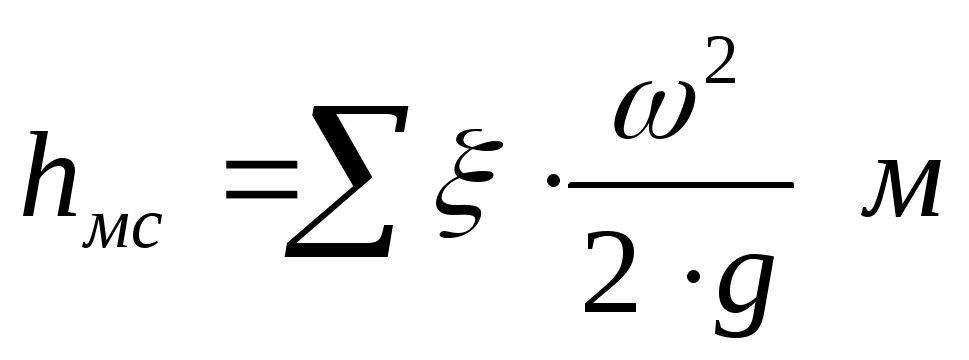
84]
Коэффициенты разных местных сопротивлений находят, как правило, опытным путем таблицы значений этих коэффициентов (или эмпирические камеры и формулы для них) содержатся в инженерных справочниках и руководствах по гидравлике. Для некоторых практически важных случаев значения коэффициентов местных сопротивлений удалось получить также и теоретическим путем. [c.199]
Как правило, коэффициенты местных сопротивлений можно найти из таблиц, составленных на основании опытных данных. [c.212]
Примечания к таблице. 1. О выходе трубы см. формулы (4-135) —(4-136). 2. Коэффициенты местного сопротивления, рекомендуемые в табл. 4-25, относятся к формуле [c.203]
При ламинарном движении Re /2) р, где – коэффициент местного сопротивления зависит от конфигурации газоходов и берегся по справочным таблицам. [c.275]
| Таблица 4.12. Коэффициенты местных сопротивлений трубопроводов |
Таблица 5,30. Коэффициенты местных сопротивлений для расчета систем водяного и парового отопления [1]
|
| Таблица 5.31. Коэффициенты местных сопротивлений элементов отопительных систем |
| Таблица 5-15 Коэффициенты местных сопротивлений С в напорных системах |
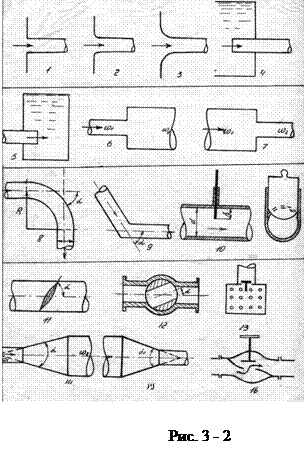
Проходя через не полностью открытую задвижку или другое подобное препятствие, поток теряет часть своей энергии.
На рис. 17, г показана картина огибания потоком выступающей задвижки. Здесь перед задвижкой наблюдается типичное сужение потока, за задвижкой— расширение. Потери напора вычисляются по формуле (48), причем коэффициент местного сопротивления зависит от степени открытия задвижки, меняясь от незначительной величины при полностью открытой задвижке до бесконечности при задвижке закрытой. Для определения в этом случае служат таблицы гидравлических справочников, составленные для разных типов конструкций дросселей и разной их степени открытия. Однако некоторые местные сопротивления еще недостаточно изучены и поэтому не нашли своего отражения в литературе. В подобных случаях надо в справочниках искать какие-то аналогичные конструкции или проводить специальные исследования для определения величины Методика определения коэффициентов местных сопротивлений весьма проста местное сопротивление включается в трубу, расход жидкости в которой можно измерить. Перед местным сопротивлением и за ним для определения потерь ставят пьезометры.
Пропуская через местное сопротивление различные расходы Q, записывают потери напора и вычисляют искомый коэффициент по формуле
[c.34]
| Таблица ПЛ. Коэффициент местного сопротивления |
Значения С в этом случае определяют по таблицам гидравлических справочников, составленным для дросселей разных конструкций при разной степени их открытия.
[c.32]| Таблица 8.8. Значения коэффициента местного сопротивления для обратного затвора (рис. 8.17) |
| Таблица 8.9. Значения коэффициента местного сопротивления для пробкового крана в зависимости от угла поворота (рис. 8.18) |
| Таблица 8.11. Значения коэффициента местного сопротивления при внезапном изменении сечения потока |
| Таблица 8.10. Значения коэффициента местного сопротивления для тройников при турбулентном режиме (рис. 8.19) |
[c.56]| Таблица 11.2 Коэффициенты местных сопротивлений [26 32] |
| Таблица 4. Теоретические коэффициенты местных сопротивлений |
ТАБЛИЦА 22.53 КОЭФФИЦИЕНТЫ МЕСТНОГО СОПРОТИВЛЕНИЯ ТРОЙНИКОВ КРУГЛОГО СЕЧЕНИЯ С УГЛОМ а = 30° В РЕЖИМЕ ВСАСЫВАНИЯ СИСТЕМ АСПИРАЦИИ [c.239]
К числу местных сопротивлений принадлежит вход в трубу условия входа заметно влияют на значения коэффициента этого местного сопротивления наименьшее значение имеет место при закругленной входной кромке данные о коэффициенте С этого местного сопротивления содержатся в таблице 4, [c.193]
Местные сопротивления при движении воды сквозь литые отводы, всасывающие, тарельчатые и обратные клапаны могут быть рассчитаны по данным таблицы 5.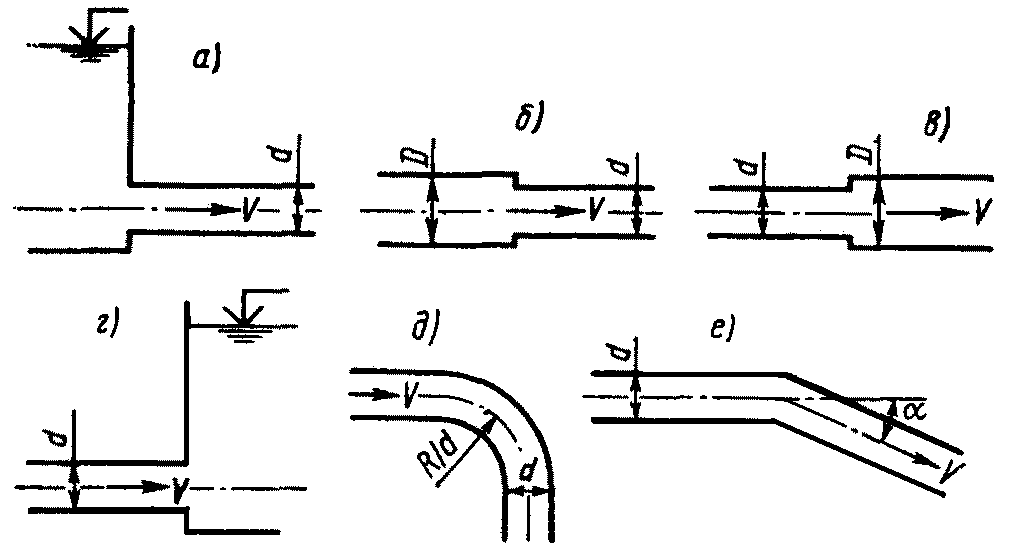
Коэффициент С для отводов зависит, вообще говоря, от отношения радиуса р кривизны его оси 7 в. с. Яблонский
[c.193]
| Таблица 4.3. Значения коэффициентов А и для некоторых местных сопротивлений |
Примечания. 1. Для газопроводов котлов под наддувом принимаются большие значения. 2. В таблице обозначены — суммарный коэффициент местных сопротивлений (учитываются только сопротивления, имеющие квадратичную или близкую к ней зависимость от скорости) I — длина участка, для кбторого определяется суммарный коэффициент местных сопротивлений ir. в — температура горячего воздуха i — температура воздуха в месте входа его в вентилятор.
[c.347]
Здесь — коэффициент местного сопротивления при движении чистого воздуха, который берется из таблиц, приведенных в Нормах расчета и проектирования пылеприготовительных установок ЦКТИ [Л. 6]. Нижеприведенные значения Q извлечены в качестве примера из указанных таблиц для БШМ 3,5 для сепаратора пыли 2,4—3,0 для циклона 1,8 для воздухораспределительной коробки 1,8 —2,5 для горелки ТКЗ 2,8 для горелки OPIРЭС при углах раздачи а = 120 3 для горелки ОРГРЭС при угле раздачи a=9 J° 2 для угловой горелки ЦККБ 1,7. [c.385]
| Таблица 8.6. Значения коэффициента местного сопротивления для задвижки Лудло в зависимости от степени ее открытия (рис. 8.12) |
15, суммируют, записывают сумму в гр. 15 и затем в rp.11. Суммируют данные граф 10 и 11, результат записывают в гр. 12. В данном случае на участке 1 имеются местные сопротивления, для кoтof)ыx их к.м.с. следующие к.м.с. местного отсоса
[c.146]Местные потери напора — Водоснабжение, Водоотведение, Гидравлика
На этой странице собрана информация по коэффициентам местного сопротивления, которые могут быть использованы для расчета местных потерь напора в задачах инженерной практики
Задвижка
При расчете трубопроводных систем коэффициент сопротивления открытой задвижки принимается ζзадв = 0,1 — 0,2. Если задвижка прикрыта на определенную величину, то коэффициент сопротивления напрямую зависит от степени закрытия. Ниже представлена таблица зависимости коэффициента сопротивления задвижки от степени закрытия. Чем больше степень закрытия — тем больше коэффициент сопротивления.
| Степень закрытия (d-h)/d | 1/8 | 2/8 | 3/8 | 1/2 | 5/8 | 3/4 | 7/8 |
| ζзадв | 0,07 | 0,26 | 0,81 | 2,06 | 5,52 | 17,0 | 97,8 |
Шаровой кран
Коэффициент сопротивления шарового крана зависит от его диаметра (условного прохода).
Ниже представлена таблица с коэффициентами. Диаметр крана приведен в дюймах (т.к. чаще всего он соединяется с трубами на резьбе), но ниже дан соответствующий диаметр в мм
| D, дюймы | 1/2 | 3/4 | 1 | 1 1/4 | 1 1/2 | 2 |
| D, мм | 15 | 20 | 25 | 32 | 40 | 50 |
| ζ | 0,26 | 0,13 | 0,12 | 0,11 | 0,103 | 0,101 |
По правилам русского языка, в отношении, в данном случае, запорной арматуры, элементом которой является шар, правильное произношение и написание будет шаровой кран, а не шаровый кран. Шаровый означает цвет (дымчато-серый)
Википедия
Вентиль
Коэффициент местного сопротивления вентиля для расчетов может быть принят равным 6
ζвент = 6
Поворотный затвор
Коэффициент сопротивления поворотного затвора для технических расчетов может быть принят равным 0,15 — 0,25
.
Обратный клапан
Коэффициент сопротивления обратного клапана для технических расчетов может быть принят равным 1,7
.
Плавный поворот
Коэффициент сопротивления при плавном повороте потока зависит от угла поворота ( α ) . Для стандартных отводов на 90о коэффициент ζ = 0,5 — 0,6. Коэффициент сопротивления при повороте на произвольный угол ( α ) может быть найден по формуле: ζпов = ζ90·α/90
Резкий поворот
Коэффициент местного сопротивления при резком повороте зависит от угла поворота ( α ). Эта зависимость представлена в табличной форме ниже
| α | 0 | 20 | 30 | 45 | 60 | 75 | 90 | 110 | 130 | 150 | 180 |
| ζпов | 0 | 0,13 | 0,16 | 0,32 | 0,56 | 0,81 | 1,19 | 1,87 | 2,59 | 3,20 | 3,60 |
Внезапное расширение
Потеря напора может быть рассчитана по скорости до (v₁) или после изменения диаметра (v₂)
Внезапное сужение
Потеря напора на внезапное сужение может быть также рассчитана по скорости (v₂) после сужения по формуле ниже:
Плавное расширение (переход расширяющийся)
Коэффициент местного сопротивления для стандартного расширяющегося перехода может быть принят ζпер.расш. = 0,25
! При вычислении потери напора скорость берется по меньшему диаметру !
.
Плавное сужение (переход сужающийся)
Коэффициент местного сопротивления для стандартного сужающегося перехода может быть принят ζпер.суж. = 0,1
При вычислении потери напора скорость также берется по меньшему диаметру
Обратный клапан с сеткой
При вычислении потерь напора на обратном клапане с сеткой, который устанавливается в определенных случаях на всасывающем трубопроводе от насоса для забора воды из водных объектов, коэффициент местного сопротивления может быть принят: ζобр.кл = 5,0 – 10,0
.
Вход в трубу
а) ζвх = 0,5
б) ζвх = 0,2
в) ζвх = 0,15
г) ζвх = 0,5 — 1,0
Коэффициент местного сопротивления при входе в трубу из резервуара зависит от того, как «оформлено» место входа. Скругленные кромки (вариант Б) уменьшают гидравлическое сопротивление. Если труба заведена вовнутрь (вариант Г), то коэффициент сопротивления, напротив, больше.
Вход в трубу с поворотом
Коэффициент сопротивления при входе в трубу из резервуара ζвх.α также зависит от угла поворота α. Чем больше угол — тем больше местное сопротивление.
| α | 90 | 75 | 60 | 45 |
| ζвх.α | 0,50 | 0,59 | 0,70 | 0,81 |
Выход в резервуар под уровень жидкости
Потери напора при выходе из трубопровода в резервуар под уровень жидкости равняются скоростному напору потока в месте выхода, т.е. коэффициент сопротивления ζвых = 1
.
Потери, связанные с течением жидкости через тройники
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Инженерное ремесло / / Падение давления, потери давления на трение. / / Коэффициенты местных гидравлических сопротивлений (коэффициенты потри напора) трубопроводов (труб), кранов, клапанов, фильтров, стояков, сгонов, переходов, углов, тройников и др. элементов систем трубопроводов и гидравлики. / / Коэффициент местного гидравлического сопротивления диафрагмы, дроссельной шайбы, сужающей диафрагмы, orifice plate, restriction plate. Коэффициент дросселирования f. Поделиться:
| ||||||||||||||||||||||||||||||
| Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | |||||||||||||||||||||||||||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | ||||||||||||||||||||||||||||||
Определение значений коэффициентов местных сопротивлений
ЗНАЧЕНИЯ КОЭФФИЦИЕНТОВ СОПРОТИВЛЕНИЯ ДЛЯ ОПРЕДЕЛЕНИЯ ПОТЕРЬ НАПОРА НА МЕСТНОЕ СОПРОТИВЛЕНИЕ (ПО ДАННЫМ Н. Н. ПАВЛОВСКОГО И ДР.) [c.289]ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ КОЭФФИЦИЕНТОВ МЕСТНЫХ СОПРОТИВЛЕНИЙ [c.111]
ОПРЕДЕЛЕНИЕ ЗНАЧЕНИИ КОЭФФИЦИЕНТОВ МЕСТНЫХ СОПРОТИВЛЕНИИ [c.111]
ЗНАЧЕНИЯ КОЭФФИЦИЕНТОВ СОПРОТИВЛЕНИЯ ДЛЯ ОПРЕДЕЛЕНИЯ ПОТЕРЬ НАПОРА НА МЕСТНОЕ СОПРОТИВЛЕНИЕ [c.324]
Тройники. Коэффициенты определяют в зависимости от отношения расхода жидкости в ответвлении к общему расходу в основном трубопроводе (магистрали). При определении потерь напора с использованием приведенных ниже коэффициентов следует исходить из скорости жидкости в магистрали. Коэффициенты местных сопротивлений, относящиеся к магистрали ( ) и к ответвляющемуся трубопроводу ( отв), в ряде случаев могут иметь отрицательные значения, так как при слиянии или разделении потоков возможно всасывание жидкости и увеличение напора [c.15]
Коэффициенты различных местных сопротивлений в большинстве случаев находят опытным путем их средние значения приводятся в справочной литературе. В табл. П-1 представлены примерные значения коэффициентов наиболее широко распространенных местных сопротивлений, С учетом выражений (11,93) и (11,101) расчетное уравнение (П,89) для определения общей потери напора может быть представлено в виде [c.90]
ТАБЛИЦА 5.31. Значение коэффициента а для определения эквивалентных длин местных сопротивлений [c.531]
Гидравлические потери в прямотрубных аппаратах. Потери давления при движении теплоносителей в прямотрубных аппаратах рассчитываются по рекомендациям, изложенным в 2.6. При этом основная трудность расчета заключается в правильном определении коэффициентов сопротивления трения и коэффициентов местных сопротивлений В общем случае коэффициент зависит от режима течения жидкости, определяемого значением числа Ке, геометрических характеристик проточной части аппарата, шероховатости стенок, соприкасающихся с движущимся потоком. Для гладких прямых каналов при ламинарном изотермическом режиме течения справедлив закон Хагена — Пуазейля [c.77]
Коэффициент местного сопротивления при выходе из трубы вых = 1- Подставив в зависимость для определения потерь напора кг1 приведенные выше значения, получим [c.357]
Для количественного определения /ак необходимо знать величину потерь полного давления на сетках. Коэффициент сопротивления сеточного пакета , входящий в формулу (4.37), является сложной функцией скорости набегающего потока, площади живого сечения сетки, числа их рядов, интенсивности орошения и вязкости раствора пенообразователя. В работе 117 ] приводится график зависимости коэффициента 4 от относительной площади живого сечения сетки (рис. 4.15). В той же работе указывается, что в случае многорядного пакета сеток значение коэффициента местного сопротивления следует умножать на число рядов сеток. [c.135]
Однако значения коэффициентов местных сопротивлений, полученные по этой формуле, довольно суш,ественно расходятся с практическими данными Абрамовича, особенно в области малых радиусов изгиба. Это привело к необходимости предложить более точную, хотя также приближенную формулу для определения В , полученную при математической обработке практических данных [c.113]
Из формул (3-1) и (3-2) следует, что потери энергии на трение и на местные сопротивл-ения пропорциональны скоростному, или динамическому, давлению (рш 2), которое является мерой кинетической энергии потока, отнесенной к единице объема жидкости. В действительности эта зависимость значительно сложнее, так как коэффициент трения и коэффициент местного сопротивления не являются постоянными величинами, а существенно зависят от скорости течения жидкости, ее плотности и вязкости, а также диаметра трубы, по которой движется поток. При определении потерь давления по формулам (3-1) и (3-2) значения коэффициентов А, и находят из соответствующих графиков или таблиц, полученных на основании многочисленных экспериментов. [c.28]
Так как на практике значения Ке меньше, чем 2 10 , а внутренняя поверхность отводов является шероховатой, для определения истинного коэффициента местного сопротивления калача в предлагаемую формулу следует ввести поправочные коэффициенты [c.114]
Номера и значения коэффициентов местных сопротивлений 2 определяют по табл. 1У.1. При определении коэффрщиентов мест- [c.228]
Подставляя сюда ранее вычисленное значение а, получаем после преобразований формулу для определения коэффициента местного сопротивления на вход (перетекание) [c.21]
Коэффициент местного сопротивления в тех случаях, когда меняется скорость газа в газопроводе, относится всегда к определенному динамическому давлению и, следовательно, к определенному сечению. Его значения практически считают не зависящими от геометрического масштаба, скорости, состояния потока и шероховатости стен, так как влияние всех этих факторов лежит в пределах точности опытных определений коэффициента местного сопротивления. [c.185]
Различие в переходных функциях (10.18) и (10.19) объясняется тем, что при их определении в исходных уравнениях принимали квазистационарные значения коэффициентов количества движения, сопротивления трения и касательного напряжения на стенке, а вследствие нестационарности распределения местных скоростей по сечению потока эти величины имеют другие значения. [c.262]
Потери напора в напорной линии после диффузора диаметром 1000 мм, скоростьдвижения воды в которой равна 2,67 м/с, включают потери напора на поворот И ов, потери напора в тройнике А р (соединение с напорным трубопроводом) и потери напора на трение по длине линии К.дл- Для определения Ков и Кр приняты коэффициенты местных сопротивлений и суммарное значение которых равно 0,6. Соответствующие потери напора + Л р = у / 2 = О 6 2,67 /19,62 = 0,22 м. Потери напора по длине напорной линии, длина которой около 10 м, при расходе Ор = 2,1 м /с равны 0,07 м. Таким образом, общие потери напора на участке А составят [c.321]
В опубликованной в 1939 г. А. 3. Евилевичем книге [2] приведены некоторые данные для определения местных потерь напора, основанные на результатах опытов на илопроводе диаметром 200 мм. Им приведены значения коэффициентов сопротивления С для тройника в проходе, колена, крестовины в проходе, задвижки и патрубка. При этом значения 1 даны только для осадков с влажностью 96 и 98%.. Автор рекомендует принимать I постоянными независимо от скорости течения, диаметра трубопровода, а также состава и свойств осадков. [c.77]
Действительный расход потока среды отличается от теоретического значения, определяемого по формуле (18.3). Влияние реальных условий отбора давления и протекания среды корректируются коэффициентом истечения С изменение плотности среды корректируется коэффициентом сжимаемости е. Поскольку наличие местных сопротивлений (арматуры, отводов, колен и пр.) искажает распределение скорости по сечению трубопровода, то для нейтрализации этого влияния применяют прямые участки трубопроводов, до и после сужающего устройства, определенной длины. Влияние шероховатости измерительного трубопровода на коэффициент истечения С корректируется с помощью поправочного коэффициента на шероховатость внутренней поверхности измерительного трубопровода К . Коррекция коэффициента истечения на притупление в процессе эксплуатации входной кромки отверстия диафрагмы осуществляется с помощью поправочного коэффициента на притупление входной кромки отверстия диафрагмы К . С учетом этого, уравнение массового расхода принимает вид [c.476]
Расчет трубопровода, по которому перекачивается жидкость, состоит в определенпи перепада давления, необходимого для обеспечения заданного расхода и оитимального сечения трубопровода. Для определения перепада давления при заданной длине трубопровода, его конфигурации и известном количестве элементов запорной аппаратуры вычисляют потери напора Ьп. При этом линейные потери напора / тр находят с помощью уравнений (4.22) или (4.23) в зависимости от режима потока в трубопроводе. Суммарные потери напора на преодоление всех местных сопротивлений рассчитывают но формуле (4.24), в которой значение коэффициентов находят суммированием отдельпых коэффициентов местных сопротивлений. [c.43]
Для определения значений местных сопротивлений (в сочленениях) необходимо использовать результаты натурных или численных экспериментов. Для некоторых конкретных видов сочленений такие зависимости приведены в справочной литературе (для сочленений труб, полукруглых и прямоугольных каналов подобные зависимости имеются, например, в работе [66]). При настройке модели течения жидкости по разветвленным системам каналов с открытым руслом на параметры реального объекта эффективные коэффициенты Шези предлагается определять из решения соответствующей минимаксной задачи. Данный подход был впервые предложен В.Е. Селезневым и А.Л. Бойченко в монографии [4] (см. также Главу 2). В некоторых задачах имеет смысл решением минимаксной задачи подбирать не сам коэффициент Шези, а определяющие его параметры (например, эквивалентную шероховатость стенок). [c.467]
При определении коэффициентов местных сопротивлений в тех случаях, когда местное сопротивление имеет большую протяженность, например, плавный поворот, из значения потери давления, сосчитанного по показанию дифмаиометра А/ ман, следует вычесть сопротивление трения на участке трубы между точками присоединения дифмаиометра (рис. 3-3). Собственно местное сопротивление [c.33]
Так как от правильного выбора высоты дымовой трубы зависит возможность работы батареи при заданном периоде коксоваиия, основной задачей расчета является ни а коем случае не занизить против действительного сопротивление отопительной системы. Поэтому, учитывая то, что местные сопротивления неаддитивны и имеющие место в отопительной системе сложные местные сопротивления обычно больше, чем соответствующая сумма простых местных сопротивлений, Гипрококсом при расчете гидравлического сопротивления отопительной систе чы принимаются более высокие коэффициенты местных сопротивлений, чем приведенные выше. Суммарная величина сопротивления отопительной системы, получаемая в результате такого расчета, хорошо согласуется с практическими данными, а неточность определения гидравлического сопротивления какого-либо отдельно взятого узла не имеет в этом случае такого решающего значения, как при расчетах распределительных устройств. [c.441]
Оценка сопротивления конструкций хрупкому разрущению, базирующаяся на основе силовых и энергетических критериев линейной механики разрушения (критические значения коэффициентов интенсивности напряжений и поверхностной энергии), с введением поправок на размеры зон пластичности, как известно, оказалась возможной для конструкций, изготавливаемых из материалов повыщенной прочности и низкой пластичности. Однако при указанных выше подходах критических характеристик разрушения, экспериментально определенных на лабораторных образцах, оказывается недостаточно в силу их существенной зависимости от абсолютных размеров сечений, температур, скоростей и способов нагружения. В связи с этим расчет накапливаемых эксплуатационных повреждений при наличии исходных трещин должен проводиться с привлечением дополнительных критериев, к числу которых в первую очередь следует отнести критические значения коэффициентов интенсивности деформаций, температур хрупкости, характеризующих переход от одного вида разрущения к другому (от вязкого с образованием мак-ропластических деформаций к квазихрупкому и хрупкому, сопровождающемуся местными пластическими деформациями в вершине трещин). [c.152]
В действительности при неравномерном движении гидравлическое сопротивление будет зависеть не от глубины потока /г, а от толщины пограничного слоя б, которая при неравномерном движении может составлять лишь малую долю от /г. Как показал анализ, выполненный в [10], для ускоренного течения изменение местного коэффициента гидравлического сопротивления на участке стабилизации течения качественно не соответствует формуле Маннинга (рис. 1.11), а его значение в 1,5—2 раза может отличаться от значения по Маннингу. Учитывая, что неточности в определении сопротивления сводят на нет попытки наиболее точного интегрирования уравнений неравномерного движения, следует поставить вопрос о разработке методов расчета неравномерного движения, свободных от указанных недостатков. В основу таких методов может быть положена теория погранич- [c.28]
Местные потери напора – Технарь
Кроме потерь напора по длине при течении потока возникают также местные потери напора, обусловленные наличием разнообразных местных сопротивлений. Местные сопротивления – это преграды на пути потока, связанные с деформациями живого сечения потока, либо с его загроможденностью.
При этом возникают изменения скорости по величине либо по направлению. К местным сопротивлениям относятся фасонные части трубопроводов (колена, переходники, тройники, диффузоры, конфузоры…), измерительная аппаратура (диафрагмы, расходомеры…), запорная арматура (вентили, задвижки, краны, клапаны…), а также технологическое оборудование (фильтры, теплообменники…).
В зоне местных сопротивлений происходит обтекание местных преград с возникновением водоворотных зон и интенсивным обменом частицами жидкости между основным потоком и этими зонами. Этот процесс обмена частицами жидкости является основным источником местных потерь энергии.
В связи со сложностью и большим разнообразием, определение коэффициентов местных потерь теоретическим путем представляет значительные трудности, и поэтому их находят экспериментально и затем табулируют. Для определения местных потерь напора можно рекомендовать формулу Вейсбаха:
где ξм— коэффициент местных потерь.
Рассмотрим некоторые случаи потерь напора при обтекании местных сопротивлений. Внезапное расширение потока имеет теоретическое решение, которое реализуется с большой степенью точности. Решение было получено инженером Борда Ж.Ш. в 1766 г.
Соответственно, коэффициент местного сопротивления:
Если потери рассчитывают, исходя из скорости потока перед внезапным расширением, формула приобретает вид:
Тогда:
здесь S1, S2 – площади живых сечений потока перед расширением и после расширения,
V1, V2 – скорости потока до и после расширения, соответственно.
При внезапном сужении трубопровода происходит сжатие потока с возникновением водоворотных зон. Значение коэффициента местного сопротивления зависит от соотношения площадей живых сечений до сужения S1 и после сужения S2.
Гидравлическое сопротивление
Существует два типа гидравлического сопротивления: сопротивление трению и местное сопротивление. В первом случае гидравлическое сопротивление обусловлено передачей импульса твердым стенкам. В последнем случае сопротивление вызывается рассеянием механической энергии при резком изменении конфигурации или направления потока, образованием вихрей и вторичных потоков в результате отрыва потока, центробежными силами и т. Д. К категории местных сопротивлений мы обычно относим сопротивления переходников, сопел, удлинителей, диафрагм, принадлежностей трубопроводов, поворотных колен, входов в трубы и т. д.
При определении полного сопротивления (потеря давления Δp f ) используется условная суперпозиция
(1)Сопротивление трения (перепад давления по длине каналов) рассчитывается по эмпирической формуле Дарси
(2)где – коэффициент трения Муди (в 4 раза больше коэффициента трения Фаннинга – см. Коэффициент трения), 1 и D H = 4S / P – длина и гидравлический диаметр канала, ρ – плотность жидкости, u – средняя скорость потока.
Для определения местного гидравлического сопротивления (ΔP 1 ) используется формула Вайсбаха.
(3)где ζ – коэффициент местного сопротивления.
Для потока в гладких каналах коэффициент трения f зависит от условий потока и является функцией только Re = ūD H / ν. Для ламинарного потока значение для прямых труб определяется по формуле Пуазейля:
(4)Значения C зависят от формы сечения и приведены в таблице 1.
Мы можем видеть из уравнения. (2) что в ламинарном потоке перепад давления изменяется со средней скоростью движения в первой степени: линейный закон сопротивления (область I, рисунок 1). В турбулентном потоке гидравлическое сопротивление трения резко возрастает (область II). Такое повышение сопротивления связано с большими потерями энергии, связанными с пульсирующим движением турбулентных вихрей в потоке жидкости. Значение в турбулентном потоке в круглой трубе можно рассчитать по формуле Блазиуса для 5 × 10 3 ≤ Re ≤ 10 5
(5)и из формулы Никурадзе для 10 5 ≤ Re ≤ 4 × 10 6
(6)Приведенные выше формулы справедливы для течения в каналах с гладкими стенками с полностью развитыми гидравлическими и тепловыми режимами.Во входной зоне канала (длиной до 20D H ) имеет более высокое значение, чем рассчитанное по формулам. (5) и (6). На коэффициент трения влияют изменения физических свойств жидкости, вызванные изменениями температуры и действием сил плавучести.
В неровных каналах гидравлическое сопротивление увеличивается за счет образования вихрей на элементах шероховатости, приводящих к дополнительным потерям удельной энергии потока. Можно выделить три типа шероховатости:
Естественная шероховатость, образующаяся в результате длительной эксплуатации трубопроводов.
Шероховатость песка, характеризующаяся высокой плотностью и различной формой конкреций.
Искусственная (или регулярная) шероховатость, когда элементы шероховатости имеют определенную геометрическую форму и расположение.
Каждый вид шероховатости имеет свою специфику изменения коэффициента трения сопротивления от Re. В случае шероховатости песка в качестве параметра шероховатости принимается отношение радиуса трубы r 0 к средней высоте выступа δ r на поверхности стенки (k = r 0 / δ r ).До определенного значения Re сопротивление шероховатой трубы изменяется так же, как и у гладкой (рисунок 2) (в ламинарном потоке оно изменяется согласно уравнению (4) (кривая 1) в турбулентном потоке , согласно уравнению (5) (кривая 2). Это связано с тем, что сначала толщина ламинарного подслоя у стенки δlam превышает среднюю высоту выступов шероховатости (δ lam > δ r ). Re увеличивается далее, δ r становится больше, чем δ lam .Это приводит к увеличению сопротивления трения шероховатой трубы по сравнению с гладкой при превышении определенного числа перехода Re tr , значение которого зависит от параметра шероховатости: Re tr 100k. При Re> Re tr (поток самоподобия) наблюдается квадратичный закон сопротивления, когда коэффициент сопротивления трения зависит только от значения параметра k (кривая 3 на рисунке 2):. Значение для труб с промышленной шероховатостью можно оценить по формуле Колебрука-Уайта.
(7)Здесь k s – эквивалентная шероховатость песка, которая для новых труб, вытянутых из черных металлов, составляет около 0.01 мм, а для новых стальных труб – около 0,014 мм; после нескольких лет эксплуатации он увеличивается примерно до 0,2 мм. Для старых ржавых труб k s 1-3 мм и для новых оцинкованных труб 0,5 мм; для новых асбоцементных труб – 0,085 мм.
Таблица 1. Коэффициент, связывающий коэффициент трения и Re -1 в уравнении. (4)
Рис. 1. Изменение давления иона в зависимости от средней скорости.
Рисунок 2. Изменение коэффициента трения в зависимости от числа Рейнольдса.
Для искусственной шероховатости из-за ее разнообразия не существует однозначных обобщающих параметров шероховатости. В таком случае для определения гидравлического сопротивления можно использовать специальные процедуры расчета. Значения для типовой арматуры и т. Д. Приведены в книге Идельчика (1992).
В гладких изгибах и в спиральных трубах с R / r 0 ≥ 3 мы предполагаем, что ΔP 1 = 0, и влияние центробежных сил учитывается путем подстановки эффективного значения коэффициента сопротивления трения в уравнение.(2): для ламинарного потока
(8)для турбулентного течения (Re> 10 4 )
(9)где – коэффициент сопротивления трения для прямой трубы; D = 1/2 Re – число Дина, r 0 – радиус трубы, R – радиус кривизны.
ССЫЛКИ
Идельчик, I, (1992) Справочник по гидравлическому сопротивлению (2-е изд.) Бегелл Хаус, Нью-Йорк.
Шлихтинг, Х. (1979) Теория пограничного слоя , МакГроу Хилл, Нью-Йорк.
Теплообменник, Руководство по проектированию (1983) т. 1 и 2, Hemisphere Publishing Corporation.
Гидравлическое сопротивление, определяемое коэффициентом потерь
Описание
Блок местного сопротивления представляет собой общий местное гидравлическое сопротивление, такое как изгиб, колено, фитинг, фильтр, локальное изменение сечения потока и т. д. Потеря давления вызванное сопротивлением вычисляется на основе коэффициента потери давления, который обычно приводится в каталогах, технических паспортах или учебниках по гидравлике.Коэффициент потери давления может быть задан как постоянный, или таблицей, в которой оно сведено в таблицу по сравнению с числом Рейнольдса.
Перепад давления между портом A и портом B составляет:
где:
Если параметр Параметризация модели установлен на По полуэмпирической формуле падение давления связано с
объемный расход по выражению:
q = A2K⋅ρ⋅p (p2 + pcr2) 1/4
где:
q – объемный расход.
A – проходное сечение.
K – коэффициент потери давления гидравлического сопротивления.
ρ – плотность жидкости.
p Cr – минимальное давление для турбулентного поток.
Если параметр Параметризация модели установлен на По потерям
коэффициент по сравнению с таблицей , падение давления связано с объемным расходом
выражением:
, где K теперь является функцией числа Рейнольдса (Re).Его значение указывается в диалоговом окне блока в табличной форме относительно числа Рейнольдса:
где:
Для постоянного коэффициента потери давления минимальное давление для турбулентного потока, p cr , рассчитывается согласно методу спецификации ламинарного перехода:
По степени сжатия – переход от ламинарного к турбулентному режиму определяется следующими уравнениями:
p cr = ( p avg + p atm ) (1 – B lam )
где
p avg Среднее давление между клеммами блока p 3 48 atm Па
B lam Соотношение давлений при переходе между ламинарный и турбулентный режимы ( Степень перепада давления ламинарного потока параметр значение) По числу Рейнольдса – переход от ламинарного до турбулентного режима определяется следующими уравнениями:
где
Re cr Критическое число Рейнольдса ( Критическое число Рейнольдса параметр значение)
Блок предоставляет две параметризации:
По полуэмпирическим формулам– Потери давления Предполагается, что коэффициент постоянен для определенного направления потока.Режим потока может быть либо ламинарный, либо турбулентный, в зависимости от числа Рейнольдса.По коэффициенту потерь в сравнении с таблицей Re– Потери давления Коэффициент задается как функция числа Рейнольдса. Предполагается, что режим течения всегда быть неспокойным. Вы должны убедиться, что данные коэффициента потерь соответствуют этому режим потока.
Сопротивление может быть симметричным или асимметричным. В симметричном сопротивления, потеря давления практически не зависит от расхода направление и одно значение коэффициента используется как для прямого и обратный поток.Для асимметричных сопротивлений отдельные коэффициенты предусмотрены для каждого направления потока. Если указан коэффициент потерь за столом таблица должна покрывать как положительные, так и отрицательные регионы потока.
Соединения A и B служат для сохранения гидравлических портов, связанных с с входом и выходом блока соответственно.
Положительное направление блока – от порта A к порту B. означает, что скорость потока положительна, если жидкость течет из точки A в точку B, и потеря давления определяется как Δp = pA − pB ,.
Ограниченные параметры
Когда ваша модель находится в ограниченном режиме редактирования, вы не можете изменять следующие параметры:
Все остальные параметры блока доступны для изменения. В Фактический набор изменяемых параметров блока зависит от значения Параметризация модели Параметр в то время модель перешла в Ограниченный режим.
(PDF) Экспериментальное определение коэффициента местного сопротивления трубки внезапного расширения
Ю. П.Ли и др.
3.2. Давление двух секций регулирующего органа
Теоретический вывод показывает, что довольно сложно определить давление на участке 1, поэтому только
можно предположить, что это значение равно давлению на переднем конце раздел. Следовательно, в этом эксперименте измеряется давление на
на переднем конце этой секции и секции 1, см. Таблицу 1. Эксперимент показывает
, что давление в секции 1 нестабильно и есть определенные колебания.Среднее значение отклонения получается примерно
за измерения. Экспериментальные данные подтверждают определенную точность этого предположения.
3.3. Трение на боковой поверхности корпуса управления
Когда уравнение импульса применяется к корпусу управления, сила трения на боковой поверхности корпуса управления
не учитывается, чтобы сделать вывод, что коэффициент местного трения связан только с расширением коэффициент диаметра трубы
метр. В литературе [5] указывается, что причина, по которой зона вихря может продолжать движение, заключается в том, что источник энергии
получается за счет обмена импульсом от основного потока.Эта часть энергопотребления, в конечном итоге, составляет
тепла после трения с завихрением и стенкой внутри завихрения, и эта потеря называется потерей на завихрение. Поскольку потери на вихре
являются наиболее важными потерями в локальной потере напора из-за внезапного расширения трубы, пренебрежение силой трения между вихрем и стенкой приведет к существенной ошибке.
4. Дизайн экспериментального решения
Экспериментальное устройство, как показано на рисунке 2, размещено горизонтально на экспериментальном столе.Впускной трубопровод
слева соединен с трубопроводом резервуара постоянного напора, а конец выпускного трубопровода справа
управляется дроссельной заслонкой. Расход регулируется выпускным клапаном. Трубопровод эксперимента представляет собой прозрачную трубу из оргстекла
с внутренним диаметром входной трубы 16 мм, диаметром расширительной трубы
20 мм и комнатной температурой 15 градусов Цельсия.
Положения трубок пьезометра: первая трубка пьезометра установлена в крайнем положении перед внезапным расширением,
, а вторая – в крайнем положении при входе внезапного расширения.Измерения давления на этих
двух пьезометрических трубках используются для проверки предположения в теоретическом выводе о том, что давление в двух секциях контрольного тела примерно одинаково. Длина вихря на входе в трубку внезапного расширения обычно составляет
, что в пять-восемь раз превышает диаметр трубки внезапного расширения, поэтому трубки пьезометра
с третьего по шестой устанавливаются на участках 100 мм, 120 мм, 140 мм. мм, 160 мм после внезапного расширения для анализа изменения потерь энергии
.
Измерение головки пьезометра: прозрачная труба из оргстекла с внутренним диаметром 6 мм и высотой 100
мм закреплена на подъемной пластине для испытания давления с минимальной шкалой в мм.
Измерение расхода: для измерения расхода применяется объемный метод. Мерный цилиндр и чашка
используются для измерения объема, а электронный секундомер используется для измерения времени.
5. Анализ экспериментальных результатов
Всегда наблюдается потеря напора, которая монотонно уменьшается вдоль потока из-за вязкости жидкости; Головка трубки пьезометра
отражает потенциальную энергию потока, поэтому верхняя часть трубки пьезометра может подниматься, опускаться или оставаться неизменной.Что касается внезапной расширительной трубы, то увеличение сечения перелива приводит к уменьшению среднего расхода
сечения и уменьшению напора. С уменьшением потерь энергии и напора при внезапном потоке через расширительную трубку
общий напор уменьшается, в то время как напор трубки пьезометра увеличивается, когда
находится рядом с внезапной расширительной трубкой [7]. Высота потери напора на трение уменьшается в направлении потока.
Таким образом, для трубок пьезометра с третьей по шестую выбирается одно оптимальное давление, то есть давление в точке
– начальном положении участка трубы, где сопротивление трения играет доминирующую роль после окончания завихрения
, т.е.е. давление в начальной позиции секции, где линия тока полностью восстанавливается до
постепенно изменяющегося потока.
Уравнение Бернулли используется для расчета локальной потери напора из-за внезапного расширения трубы на основе фактического измерения
(см. Результаты в таблице 2).
Как показано в таблице выше, значение потери напора, рассчитанное по теоретическому уравнению, пренебрежимо мало по сравнению с фактически измеренным значением потери напора
. Значение потери напора, рассчитанное по теоретическому уравнению, в большинстве случаев составляет менее 1 мм в
, то есть, когда значение, основанное на результатах расчета, отражается в эксперименте, давление трубки пьезометра
в основном не изменяется с изменение потока.Однако это явно несоответствие –
Метод коэффициента сопротивления– Метод К
Метод коэффициента сопротивления – Метод К
Метод коэффициента сопротивления (или K-метод, или метод избыточного напора) позволяет пользователю описать потерю давления через колено или фитинг безразмерным числом – K . Это безразмерное число (K) может быть включено в уравнение Дарси-Вейсбаха аналогично методу эквивалентной длины.Вместо данных об эквивалентной длине в этом случае используется безразмерное число (K) для характеристики фитинга без привязки его к свойствам трубы.
Значение K представляет собой кратное головок скорости , которые будут потеряны при прохождении жидкости через фитинг. Таким образом, уравнение для расчета потери давления в гидравлическом элементе:
Следовательно, уравнение для расчета потери давления для всей гидравлической системы:
Значение K может быть охарактеризовано для различных режимов потока (т.е.е. согласно числу Рейнольдса), поэтому он более точен, чем метод эквивалентной длины.
Есть несколько других методов расчета потери давления для фитингов, эти методы более сложные и также более точные :
- 2K-метод . Метод 2K – это метод, разработанный Hooper B.W. чтобы спрогнозировать потерю напора в локтевом, клапанном или тройнике Метод 2K улучшает метод избыточного напора, характеризуя изменение потери давления из-за изменения числа Рейнольдса .Метод 2-K имеет преимущество перед другими методами, особенно в области ламинарного потока .
- 3K-метод . Метод 3K (разработанный Роном Дарби в 1999 г.) дополнительно повышает точность расчета потери давления, также характеризуя изменение геометрических пропорций фитинга по мере изменения его размера. Это делает метод 3K особенно точным для системы с большими фитингами .
Коэффициент местного сопротивления | Научный.Нетто
Потери давления степенного потока жидкости при осесимметричном внезапном сжатииАвторы: Евгений Борзенко, Кира Бояркина, Геннадий Р. Шрагер
Аннотация: В статье исследуется ламинарное стационарное степенное течение жидкости при осесимметричном сжатии трубы. Математическая постановка задачи сформулирована с использованием переменных функции тока и завихренности.Для получения стационарного решения используется релаксационный метод с последующей реализацией численного алгоритма на основе конечно-разностной схемы альтернативных направлений. Проведенные параметрические исследования позволяют получить зависимость коэффициентов местного сопротивления от числа Рейнольдса, степени нелинейности и степени сжатия трубопроводов.
47
Эксперимент по влиянию расстояния между диафрагмами и локальным коэффициентом сопротивления в трубопроводе нагнетания давленияАвторы: Линь Ли, Шэн Цзинь, Чжао Лян Бай
Аннотация: Чтобы исследовать правило влияния расстояния между диафрагмами на коэффициент местного сопротивления и общие локальные потери напора воды, было проведено экспериментальное исследование путем установки двух различных относительных расстояний между диафрагмами в напорном трубопроводе.Результаты экспериментов показали, что: При относительном расстоянии, результаты общих локальных потерь напора воды, рассчитанные по традиционной гидравлической формуле с реальными измеренными данными, максимальная относительная погрешность была менее 3%. Это показало, что при большом относительном расстоянии нет необходимости учитывать влияние относительного расстояния между пластинами с отверстиями. Однако, когда относительное расстояние, реальные измеренные данные общих местных потерь воды были намного меньше расчетных данных по традиционной формуле расчета, максимальная относительная погрешность была достигнута 239.5%. Было объяснено, что, когда относительное расстояние было относительно небольшим, существовало соседнее влияние между пластинами с отверстиями, поэтому общие локальные потери воды с помощью пластин с несколькими отверстиями не равнялись сумме каждой потери напора воды с помощью пластины с одним отверстием, и общая локальная потеря напора не обязательно увеличивалась с увеличением количества диафрагм. Связано ли увеличение общих локальных потерь напора воды с относительным расстоянием до диафрагм.Традиционная формула расчета местной потери напора в гидравлике должна быть исправлена и изменена.
1092
Коэффициент сопротивления потоку – обзор
E ПОТОКУ СОПРОТИВЛЕНИЕ (ИМПЕДАНС)
Глобальный баланс импульса, уравнения. (42), (44) и (47), соответственно, для компонента, одиночного контура и системы контуров содержат члены трения сопротивления потоку ∆p fr и потери формы ∆ p форма .Член трения (сдвиг стенки) пропорционален массовому расходу W только при малых числах Рейнольдса. Потери формы всегда пропорциональны квадрату массового расхода Вт 2 . В большинстве случаев поток является турбулентным, и потери на трение и форму пропорциональны приблизительно W 2 и всегда зависят от направления потока. Однако следующий метод построения матрицы сопротивления потоку или импеданса для турбулентных потоков применим к любому показателю степени n в W n .
При объемном и массовом расходах, предсказываемых уравнениями. (46), или (62), и (57), и (33), непосредственно оценивают необратимую диссипацию в терминах сопротивления каждого компонента (индекс i ) в каждом сегменте контура (с индексом j и входной массовый расход Вт j ) между точками ответвления контура (с индексом k ):
(74) ∑i∈j (Δpfr + Δpform) i = RkjWWj
(75) Rkj = ∑i∈j12ρliKi + ϕl02fiKi / dh, iAi2
, где повторяющиеся индексы в уравнении.(74) не подразумевают суммирования, ρ l – эталонная (жидкая) плотность, подразумеваемая в определении множителя двухфазного трения ϕlo2 [18], f – коэффициент трения стенки Дарси, K потеря формы [см. (37)], смоделированный для учета эффектов двухфазного потока, а R k – это коэффициент полного сопротивления для сегмента контура j в контуре k . Для f , ϕlo2 и K мы отсылаем читателя к стандартным текстам [2, 8, 24, 28].Уравнение (37) показывает, что K зависит от направления потока. Общее сопротивление потоку в уравнении. (74), следовательно, пропорционально W | W |, а не W 2 . Корреляции для f , ϕlo2 и K применяются глобально для всего компонента, а не локально, и получены из стационарных экспериментов. W поэтому приблизительно не зависит от местоположения между точками ответвления.
В уравнении. (74) единый коэффициент сопротивления потоку, R k , представляет гидравлические сопротивления всех компонентов в сегменте контура.Это демонстрирует первое уменьшение потенциально очень большого количества коэффициентов сопротивления, связанных со всеми неоднородностями площадей поперечного сечения потока в гидравлической системе. Интегральные методы подтверждают, что распределение гидравлического сопротивления между точками разветвления в петлевой системе несущественно для прогнозирования тепловых и кинематических возмущений.
Это инструкция для оценки распределения гидравлического сопротивления в петлевой системе и, в частности, для масштабирования интегральных средств тестирования [41], чтобы построить из коэффициентов сопротивления R kj матрицу сопротивления потока P.Матрица сопротивления потока P наглядно отображает комбинацию коэффициентов сопротивления, которая управляет распределением потока в системе контуров и перекрестной связью между контурами по импедансу. Матрица P импеданса потока отображает характеристики сопротивления, относящиеся к топологии системы , тогда как динамическое состояние системы представлено вектором H кинетической энергии. Матрица сопротивления потока P слабо изменяется со временем по мере изменения плотности жидкости и, возможно, числа Рейнольдса (при низких числах Рейнольдса).
Основная идея состоит в том, чтобы выразить вектор сопротивления в формуле. (47) с точки зрения только тех же первичных массовых расходов N L , которые связаны с первичными объемными расходами N L , которые получены в соответствии с уравнением. (62), из известных импульсов петли N L .
( N L + N B – 1) независимые массовые расходы смеси W м (0, т ) петлевой системы сгруппированы в N L первичный, Вт м , пр (0, т ) и ( N B -1) вторичный, Вт м , sn (0, т ), скорости потока и расположены в том же порядке, что и объемные скорости потока в уравнении.(50). Основные массовые расходы, Вт м , пр (0, т ), затем задаются уравнениями. (62) и (33), в то время как вторичный массовый расход ( N B -1) определяется как
(76) Wm, sn0tp = −Ar − 1piBriq [Wm, pr0tq
i вектор сопротивления петли в формуле. (47) разбивается таким же образом, как и импульс петли в уравнении. (50); то есть
(77), где индексы p и q подразумевают суммирование, E – это N L × N L матрица элементов сопротивления R ip , определенная в уравнении .(75) и связанные с сегментами контура первичного потока W м, pr , а Z – матрица N L × ( N B – 1) элементы сопротивления R iq , также определенные в формуле. (75), но связаны с сегментами контура вторичного контура расхода W м, sn . Матрицы E и Z получаются простой заменой элементов инерции в A и X, соответственно, элементами сопротивления соответствующих сегментов контура.
Матрица сопротивления потока P N L × ( N L + N B – 1) равна E, дополненная Z,
(78) P = EZ
и необходимо умножить на ( N L + N B – 1) × 1 вектор-столбец направленной кинетической энергии
(79) H¯ = H¯prH¯snT
для получения элементов [ см. уравнение. (77)] вектора сопротивления в уравнении. (47). Первые N L элементов H ¯ даются как
(80) H¯pr = Wm, prtWm, prtl… Wm, prtWm, prtNLT
и последние ( N B – 1) элементы H¯ задаются
(81) H¯sn = Wm, sntWm, sntl… Wm, sntWm, sntNB − 1T
, где каждый элемент вектора задается уравнением.(76). Условные обозначения определяют матричную алгебру для генерации вектора сопротивления в формуле. (47):
(82) PijHj = ZipHprp + EiqHsnq
Рассмотрим снова четыре цикла, 1 , ℭ 2 , ℭ 3 и ℭ 4 на рис. , сегментов с метками (1, 4,5,7), (2,4,5,7), (3,4,5,7) и (1,4, 6, 7) и имеющих основные сегменты 1, 2, 3 и 5. Для иллюстрации матрица импеданса (4 × 7) для четырех контуров равна
(83) P = R100R5R40R70R20R5R40R700R3R5R40R7R1000R4R6R7
, а семимерный вектор направленных кинетических энергий равен в соответствии с уравнениями.(79), (80) и (81),
(84) H¯ = W1W1W2W3W3W3W5W5W1 + W2 + W3W1 + W2 + W3W1 + W2 + W3 + W5W1 + W2 + W3 + W5W1 + W2 + W3W1 + W2 + W3
Пространственная зависимость массовых расходов в уравнениях. (80), (81) и (84) опускаются, потому что поток считается квазистационарным, что согласуется с корреляциями для расчетов потери давления на трение и потери формы. Вульф [41] ранее ввел более сложное умножение более простой и компактной формы матрицы импеданса на более сложную матрицу направленных кинетических энергий.Стандартное умножение матрицы на вектор, представленное здесь в формуле. Однако формула (82) является предпочтительной, поскольку направленная кинетическая энергия выглядит как простой вектор H¯. P четко отображает импедансную связь между контурами, и мы приходим к следующей интерпретации P.
Относительные величины элементов в каждой строке P в уравнениях. (78) и (83) показывают распределение сопротивления потока в контуре, связанном с этим рядом. Петли, которые имеют общий элемент в одном или нескольких столбцах , связаны с импедансом , и тем сильнее, чем больше общий элемент относительно других элементов в соответствующей строке.
| Изменение раздела | К | |
| – Восстановление концентрический – élargissement d1 / d2 = 0,90 | 0,026 | |
| – Восстановление концентрический – большой размер d1 / d2 = 0.80 | 0,13 | |
| – Восстановление концентрический – élargissement d1 / d2 = 0,75 | 0,16 | |
| – Восстановление концентрический – élargissement d1 / d2 = 0,67 | 0.28 | |
| – Восстановление концентрический – élargissement d1 / d2 = 0,50 | 0,5 | |
| – Восстановление концентрическая ретрециссия d1 / d2 = 0,90 | 0,008 | |
| – Восстановление концентрический – ретроградный d1 / d2 = 0.80 | 0,041 | |
| – Восстановление концентрический – ретроградный d1 / d2 = 0,75 | 0,049 | |
| – Восстановление концентрический – ретроградный d1 / d2 = 0,67 | 0.085 | |
| – Восстановление концентрический – ретроградный d1 / d2 = 0,50 | 0,16 | |
| Вход и пролетный трубопровод | ||
| – Вход кондукт de niveau – r / d = 0.00 (угол vif) | 0,5 | |
| – Вход кондукт de niveau – r / d = 0,02 | 0,28 | |
| – Вход Conduite de niveau – r / d = 0,04 | 0.24 | |
| – Вход Conduite de niveau – r / d = 0,06 | 0,15 | |
| – Вход Conduite de niveau – r / d = 0,10 | 0,09 | |
| – Вход pipeite de niveau – r / d> 0.15 (Биен Арронди) | 0,04 | |
| – Вход кабельный сайлланте | 0,78 | |
| – Вылет канализации | 1 | |
| Дайверы | ||
| Comptage (Consulter normalement le factory) | ||
| – Compteur à диск (K: 3,4 до 10) | 10 | |
| – Compteur rotatif | 10 | |
| – Compteur à поршень | 15 | |
| – Compteur à турбина (K: 5-7.5) | 7,5 | |
| Филиал радиаторы y / c robinetterie | ||
| – Piquage sur Réseaux Aller et Retour, Radiateur, Robinetterie | 15 | |
| Ансамбль chaudière y / c robinetterie | ||
| – вход et sortie chaudière y / c изменения brusques de section, Entrée et sortie, vanne, tuyauterie de dérivation, piquage, du vase d’expansion (8-12) | 12 | |
| Тронсон вторые 2 фотографии | ||
| – без вариаций из раздела | 1. | |