Расширительные баки для отопления — рассчёт объёма воды при нагревании
- Техподдержка
- Статьи
- Архив
- Расчет расширительного бака для отопления
Как известно, подавляющее большинство веществ в природе обладает свойством расширяться с повышением температуры. Соответствующей характеристикой служит коэффициент теплового расширения, отображающий изменение объема среды либо линейных размеров тела при нагреве на 1 °С в условиях постоянного давления (в первом случае говорят о коэффициенте теплового объемного, во втором – линейного расширения).
Рис. 1. Зависимость объема воды от температуры
Коэффициент температурного расширения воды
С увеличением температуры коэффициент объемного теплового расширения воды изменяется неравномерно (рис. 1): в диапазоне от 0 до 4 °С объем воды и вовсе уменьшается (эта особенность играет важную роль в природных водоемах), при дальнейшем нагреве значение коэффициента меняется так, как показано в табл. 1.
1.
Таблица 1
| Температура воды, °C | Коэффициент объемного теплового расширения, К-1 |
| 5–10 | 0,53·10-4 |
| 10–20 | 1,50·10-4 |
| 20–40 | 3,02·10-4 |
| 40–60 | 4,58·10-4 |
| 60–80 | 5,87·10-4 |
Вот, что это означает на практике. Примерный объем воды в системе отопления индивидуального дома тепловой мощностью 30 кВт составляет 450 л (в ориентировочных расчетах допускается принять 15 л/кВт). В табл. 2 приведены расчеты, показывающие, что при нагреве с 5 до 80 °C увеличение этого объема составит порядка 13 л.
Таблица 2
| Температура воды, °C | Коэффициент объемного теплового расширения, К-1 | Увеличение объема, л |
| 5–10 | 0,53·10–4 | 0,119 |
| 11–20 | 1,50·10–4 | 0,675 |
| 21–40 | 3,02·10–4 | 2,718 |
| 41–60 | 4,58·10–4 | 4,122 |
| 61–80 | 5,87·10-4 | 5,283 |
|
|
|
Итого: 12,917 (2,87 %) |
Чтобы принять дополнительный объем жидкости, образующийся при ее нагревании, систему отопления оснащают расширительным баком (экспанзоматом). Раньше в этом качестве широко использовались открытые (с доступом атмосферного воздуха) резервуары, размещаемые в верхней точке системы – как правило, на чердаке дома. Такое решение, хотя применяется и сегодня, не соответствует современным требованиям к элементам отопительных систем, и предпочтение отдано мембранному расширительному баку: его можно устанавливать в любом месте дома (в том числе – непосредственно в котельной), в нем не происходит попадания кислорода в теплоноситель (т.е. исключается основной фактор коррозии оборудования), а рабочая жидкость не теряется из-за испарения.
Раньше в этом качестве широко использовались открытые (с доступом атмосферного воздуха) резервуары, размещаемые в верхней точке системы – как правило, на чердаке дома. Такое решение, хотя применяется и сегодня, не соответствует современным требованиям к элементам отопительных систем, и предпочтение отдано мембранному расширительному баку: его можно устанавливать в любом месте дома (в том числе – непосредственно в котельной), в нем не происходит попадания кислорода в теплоноситель (т.е. исключается основной фактор коррозии оборудования), а рабочая жидкость не теряется из-за испарения.
Если в открытой системе отопления тепловое расширение воды приводит к увеличению ее объема с перемещением образующегося «излишка» в расширительный бак, то в замкнутом трубопроводе результатом окажется повышение давления.
Значение Δp прямо пропорционально коэффициенту теплового расширения и обратно пропорциональна коэффициенту объемного сжатия воды (зависит от давления, в диапазоне 1–25 бар – 49,51∙10-11 Па, в гидравлических расчетах принимают равным 4,9 ∙10-10 Па):
Δp = βt • Δt / βv, Па.
Представленные в табл. 3 результаты расчетов показывают, каким значительным является увеличение давления при нагреве воды на 75 °C в замкнутом трубопроводе – в разы выше давления разрушения полнобиметаллического радиатора, не говоря уже о других элементах отопительной системы. Поправка на деформацию труб и оборудования уменьшит это значение, но не изменит ситуации кардинально.
Таблица 3
| Температура воды, °C | Коэффициент объемного теплового расширения, К-1 | Увеличение давления, бар (1 бар = 0,1 МПа) |
| 5–10 | 0,53·10-4 | 5,41 |
| 11–20 | 1,50·10-4 | 30,61 |
| 21–40 | 3,02·10-4 | 123,26 |
| 41–60 | 4,58·10-4 | 186,93 |
| 61–80 | 5,87·10-4 | 239,59 |
|
|
|
Итого: 346,21 |
Конструкция расширительных баков
Помимо обязательности расширительного бака, полученные цифры показывают важность его правильного подбора (при недостаточном объеме неизбежно разрушение мембраны), а также необходимость компенсации теплового расширения воды в замкнутом трубопроводе даже при относительно небольшом перепаде температур.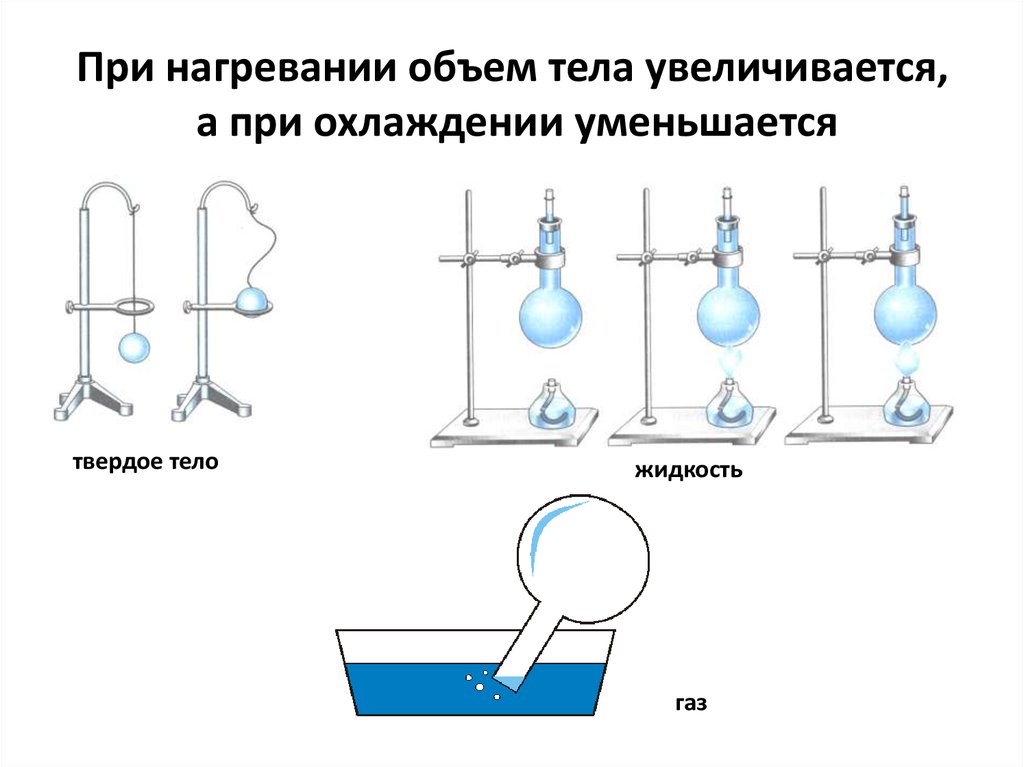 Например, аварийная ситуация может возникнуть в системе холодного водоснабжения квартиры при самопроизвольном нагреве поступившей воды до комнатной температуры и закрытом кране на вводе.
Например, аварийная ситуация может возникнуть в системе холодного водоснабжения квартиры при самопроизвольном нагреве поступившей воды до комнатной температуры и закрытом кране на вводе.
Существуют две основные конструкции мембранных расширительных баков. Наиболее простая – с диафрагменной (лепестковой) мембраной, наглухо зафиксированной в месте соединения полукорпусов. Такие модели имеют меньшую стоимость и применяются достаточно широко, однако обладают недостатками, основные из которых – контакт теплоносителя с материалом корпуса и невозможность ремонта при повреждении мембраны. Баки второго типа оборудуется сменной мембраной – баллонной либо сферической, помещаемой в корпус через горловину с фланцем ( рис. 2). Они ремонтопригодны, исключают коррозию металлических стенок от соприкосновения с рабочей средой, характеризуются более полным заполнением внутреннего пространства корпуса (полезный объем), чем экспанзоматы с диафрагменной мембраной.
Pис. 2. Конструкция расширительных баков со сменной мембранойVRV
Конструкция расширительных баков со сменной мембранойVRV
Принцип работы у мембранных баков обоих типов одинаковый: внутренний объем резервуара разделен эластичной перегородкой на две полости – воздушную и водяную. При нагреве жидкости в системе и увеличении ее объема происходит заполнение водяной полости с растяжением мембраны и сжатием газа (воздуха или азота) в пространстве между ней и корпусом. При остывании теплоносителя имеют место обратные процессы – сжатие жидкости и мембраны, расширение газа.
Давление воздушной подушки настраивается таким образом, чтобы при неработающей системе отопления статическое давление теплоносителя в ней было компенсировано, и мембрана находилась в равновесном состоянии (подробнее читайте в статье о расчете и размещении мембранного бака). Обычно в продажу мембранные расширительные баки поступают с предварительно настроенным давлением в 1,5 бара. Для возможности регулирования и поддержания предварительного давления мембранный бак оснащают ниппелем.
Материалами для изготовления мембран в настоящее время служат различные эластомеры – натуральная каучуковая (используется при изготовлении баков для холодного водоснабжения) и синтетическая резина – бутиловая, стирол-бутадиеновая (SBR), нитрил-бутадиеновая (NBR), а также этилен-пропилен-диен-мономер (EPDM), хорошо зарекомендовавший себя в инженерных системах различного назначения. Мембраны из EPDM эластичны, термостойки, гигиеничны и долговечны (ресурс оценивается в 100 тыс. циклов динамического нагружения), поэтому широко применяются в баках для отопления и водоснабжения, включая питьевое. В нормально работающих системах отопления мембраны экспанзоматов не подвержены резким динамическим воздействиям (изменение объема теплоносителя происходит достаточно плавно), поэтому основными требования к ним являются термическая стойкость и долговечность. EPDM как нельзя лучше отвечает этим критериям.
Производство мембран расширительных баков нормируются европейским стандартом DIN 4807-3 «Расширительные емкости, мембраны из эластомеров для расширительных баков.
На рис. 3 показаны сменные мембраны из EPDM. Их крепление к фланцу бака осуществляется с помощью контрфланца с приваренным присоединительным штуцером и дырчатым рассекателем струи по центру. В случае порыва мембраны (если такое все же произошло) ее несложно извлечь, чтобы заменить на новую или отремонтировать (повреждение можно заклеить самостоятельно или обратиться в ближайший шиномонтаж для вулканизации).
Рис. 3. Сменные EPDM-мембраны для расширительных баков
Корпус мембранного расширительного бака, как правило, изготавливают из пластичной углеродистой стали методом холодной глубокой штамповки с последующей покраской эпоксидной эмалью. Внутреннюю поверхность экспанзоматов со сменной мембраной обычно не окрашивают, и чтобы исключить риск ее коррозии при выпадении конденсата, в воздушную полость на заводе закачивают химически нейтральный азот.
Как правило, вертикальные баки емкостью от 50 л оборудуют опорами-ножками для напольной установки. Модели меньшего объема (обычно – до 35 л включительно) подвешивают непосредственно на трубопровод или крепят к стене с помощью специальных кронштейнов (консолей).
В табл. 4 приведены характеристики мембранных расширительных баков VALTEC VRV.
Таблица 4. Технические характеристики расширительных баков VALTEC
| Характеристика | Значение |
| Рабочая температура, °С | От –10 до +100 |
| Максимальное рабочее давление, бар | 5 |
| Заводское давление газовой камеры (преднастройка), бар | 1,5 |
| Материал корпуса | Сталь углеродистая с окраской эпоксидным полиэстером красного цвета |
| Материал мембраны | EPDM |
| Тип мембраны | Сменная |
| Срок службы при соблюдении паспортных условий эксплуатации, лет | 25 |
Удобный монтаж экспанзоматов в системах мощностью до 44 кВт обеспечивает группа безопасности расширительного бака VT. 495 (рис. 4), представляющая собой полую стальную оцинкованную консоль с фланцем для крепления к стене и предустановленным комплектом сантехнических устройств из предохранительного клапана, автоматического воздухоотводчика и манометра. Имеются также два резьбовых патрубка – для подключения группы к системе и подсоединения расширительного бака. Габариты консольной группы безопасности позволяют подвешивать непосредственно к ней расширительные баки размером до 50 л включительно.
495 (рис. 4), представляющая собой полую стальную оцинкованную консоль с фланцем для крепления к стене и предустановленным комплектом сантехнических устройств из предохранительного клапана, автоматического воздухоотводчика и манометра. Имеются также два резьбовых патрубка – для подключения группы к системе и подсоединения расширительного бака. Габариты консольной группы безопасности позволяют подвешивать непосредственно к ней расширительные баки размером до 50 л включительно.
Рис. 4. Группа безопасности расширительного бака VT.495
Важным и полезным аксессуаром для расширительных баков систем отопления и ГВС является также разъемный сгон-отсекатель VT.538, позволяющий отсоединять мембранные баки от трубопровода без его опорожнения.
Уважаемые читатели! С момента публикации этой статьи в ассортименте нашей компании, практике применения оборудования, нормативных документах могли произойти изменения. Предлагаемая вам информация полезна, однако носит исключительно ознакомительный характер.
Распечатать статью:
Расчет расширительного бака для отопления
© Правообладатель ООО «Веста Регионы», 2010
Все авторские права защищены. При копировании статьи ссылка на правообладателя
и/или на сайт www.valtec.ru обязательна.
Предложена новая теория, объясняющая, почему вода при нагревании от 0 до 4°C сжимается • Юрий Ерин • Новости науки на «Элементах» • Физика
Японский физик Масакадзу Мацумото выдвинул теорию, которая объясняет, почему вода при нагревании от 0 до 4°C сжимается, вместо того чтобы расширяться. Согласно его модели, вода содержит микрообразования — «витриты», представляющие собой выпуклые пустотелые многогранники, в вершинах которых находятся молекулы воды, а ребрами служат водородные связи. При повышении температуры конкурируют между собой два явления: удлинение водородных связей между молекулами воды и деформация витритов, приводящая к уменьшению их полостей. В диапазоне температур от 0 до 3,98°C последнее явление доминирует над эффектом удлинения водородных связей, что в итоге и дает наблюдаемое сжатие воды. Экспериментального подтверждения модели Мацумото пока что нет — впрочем, как и других теорий, объясняющих сжатие воды.
Экспериментального подтверждения модели Мацумото пока что нет — впрочем, как и других теорий, объясняющих сжатие воды.
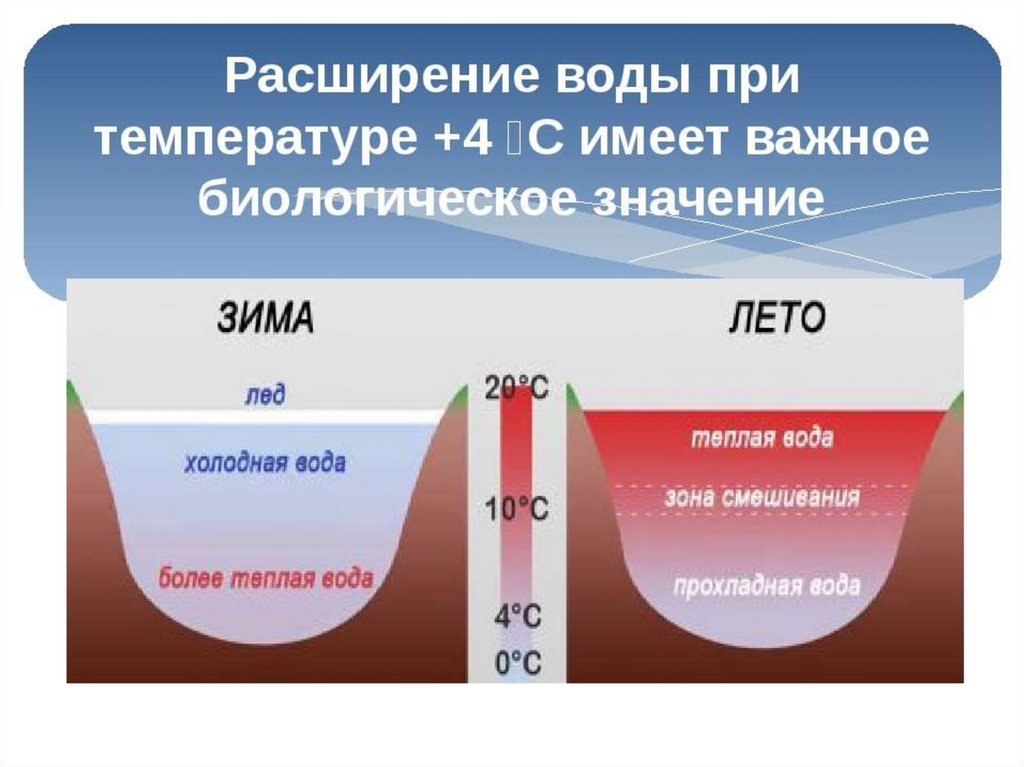
В отличие от подавляющего большинства веществ, вода при нагревании способна уменьшать свой объем (рис. 1), то есть обладает отрицательным коэффициентом теплового расширения. Впрочем, речь идет не обо всём температурном интервале, где вода существует в жидком состоянии, а лишь об узком участке — от 0°C примерно до 4°C. При больших температурах вода, как и другие вещества, расширяется.
Между прочим, вода — не единственное вещество, имеющее свойство сжиматься при увеличении температуры (или расширяться при охлаждении). Подобным поведением могут «похвастать» еще висмут, галлий, кремний и сурьма. Тем не менее, в силу своей более сложной внутренней структуры, а также распространенности и важности в разнообразных процессах, именно вода приковывает внимание ученых (см. Продолжается изучение структуры воды, «Элементы», 09.10.2006).
Некоторое время назад общепринятой теорией, отвечающей на вопрос, почему вода увеличивает свой объем при понижении температуры (рис.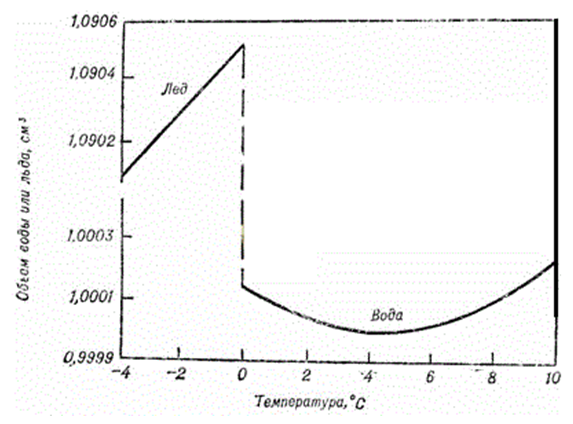 1), была модель смеси двух компонент — «нормальной» и «льдоподобной». Впервые эта теория была предложена в XIX веке Гарольдом Витингом и позднее была развита и усовершенствована многими учеными. Сравнительно недавно в рамках обнаруженного полиморфизма воды теория Витинга была переосмыслена. Отныне считается, что в переохлажденной воде существует два типа льдообразных нанодоменов: области, похожие на аморфный лед высокой и низкой плотности. Нагревание переохлажденной воды приводит к плавлению этих наноструктур и к появлению двух видов воды: с большей и меньшей плотностью. Хитрая температурная конкуренция между двумя «сортами» образовавшейся воды и порождает немонотонную зависимость плотности от температуры. Однако пока эта теория не подтверждена экспериментально.
1), была модель смеси двух компонент — «нормальной» и «льдоподобной». Впервые эта теория была предложена в XIX веке Гарольдом Витингом и позднее была развита и усовершенствована многими учеными. Сравнительно недавно в рамках обнаруженного полиморфизма воды теория Витинга была переосмыслена. Отныне считается, что в переохлажденной воде существует два типа льдообразных нанодоменов: области, похожие на аморфный лед высокой и низкой плотности. Нагревание переохлажденной воды приводит к плавлению этих наноструктур и к появлению двух видов воды: с большей и меньшей плотностью. Хитрая температурная конкуренция между двумя «сортами» образовавшейся воды и порождает немонотонную зависимость плотности от температуры. Однако пока эта теория не подтверждена экспериментально.
С приведенным объяснением нужно быть осторожным. Не случайно здесь говорится лишь о структурах, которые напоминают аморфный лед. Дело в том, что наноскопические области аморфного льда и его макроскопические аналоги обладают разными физическими параметрами.
Японский физик Масакадзу Мацумото решил найти объяснение обсуждаемого здесь эффекта «с нуля», отбросив теорию двухкомпонентной смеси. Используя компьютерное моделирование, он рассмотрел физические свойства воды в широком диапазоне температур — от 200 до 360 К при нулевом давлении, чтобы в молекулярном масштабе выяснить истинные причины расширения воды при ее охлаждении. Его статья в журнале Physical Review Letters так и называется: Why Does Water Expand When It Cools? («Почему вода при охлаждении расширяется?»).
Изначально автор статьи задался вопросом: что влияет на коэффициент теплового расширения воды? Мацумото считает, что для этого достаточно выяснить влияние всего трех факторов: 1) изменения длины водородных связей между молекулами воды, 2) топологического индекса — числа связей на одну молекулу воды и 3) отклонения величины угла между связями от равновесного значения (углового искажения).
Перед тем как рассказать о результатах, полученных японским физиком, сделаем важные замечания и разъяснения по поводу вышеупомянутых трех факторов. Прежде всего, привычная химическая формула воды H2O соответствует лишь парообразному ее состоянию. В жидкой форме молекулы воды посредством водородной связи объединяются в группы (H2O)x, где x — количество молекул. Наиболее энергетически выгодно объединение из пяти молекул воды (x = 5) с четырьмя водородными связями, в котором связи образуют равновесный, так называемый тетраэдральный угол, равный 109,47 градуса (см. рис. 2).
Прежде всего, привычная химическая формула воды H2O соответствует лишь парообразному ее состоянию. В жидкой форме молекулы воды посредством водородной связи объединяются в группы (H2O)x, где x — количество молекул. Наиболее энергетически выгодно объединение из пяти молекул воды (x = 5) с четырьмя водородными связями, в котором связи образуют равновесный, так называемый тетраэдральный угол, равный 109,47 градуса (см. рис. 2).
Проанализировав зависимость длины водородной связи между молекулами воды от температуры, Мацумото пришел к ожидаемому выводу: рост температуры рождает линейное удлинение водородных связей. А это, в свою очередь, приводит к увеличению объема воды, то есть к ее расширению. Сей факт противоречит наблюдаемым результатам, поэтому далее он рассмотрел влияние второго фактора. Как коэффициент теплового расширения зависит от топологического индекса?
Компьютерное моделирование дало следующий результат. При низких температурах наибольший объем воды в процентном отношении занимают кластеры воды, у которых на одну молекулу приходится 4 водородных связи (топологический индекс равен 4). Повышение температуры вызывает уменьшение количества ассоциатов с индексом 4, но при этом начинает возрастать число кластеров с индексами 3 и 5. Проведя численные расчеты, Мацумото обнаружил, что локальный объем кластеров с топологическим индексом 4 с повышением температуры практически не меняется, а изменение суммарного объема ассоциатов с индексами 3 и 5 при любой температуре взаимно компенсирует друг друга. Следовательно, изменение температуры не меняет общий объем воды, а значит, и топологический индекс никакого воздействия на сжатие воды при ее нагревании не оказывает.
При низких температурах наибольший объем воды в процентном отношении занимают кластеры воды, у которых на одну молекулу приходится 4 водородных связи (топологический индекс равен 4). Повышение температуры вызывает уменьшение количества ассоциатов с индексом 4, но при этом начинает возрастать число кластеров с индексами 3 и 5. Проведя численные расчеты, Мацумото обнаружил, что локальный объем кластеров с топологическим индексом 4 с повышением температуры практически не меняется, а изменение суммарного объема ассоциатов с индексами 3 и 5 при любой температуре взаимно компенсирует друг друга. Следовательно, изменение температуры не меняет общий объем воды, а значит, и топологический индекс никакого воздействия на сжатие воды при ее нагревании не оказывает.
Остается выяснить влияние углового искажения водородных связей. И вот здесь начинается самое интересное и важное. Как было сказано выше, молекулы воды стремятся объединиться так, чтобы угол между водородными связями был тетраэдральным. Однако тепловые колебания молекул воды и взаимодействия с другими молекулами, не входящими в кластер, не дают им этого сделать, отклоняя величину угла водородной связи от равновесного значения 109,47 градуса. Чтобы как-то количественно охарактеризовать этот процесс угловой деформации, Мацумото с коллегами, основываясь на своей предыдущей работе Topological building blocks of hydrogen bond network in water, опубликованной в 2007 году в Journal of Chemical Physics, выдвинули гипотезу о существовании в воде трехмерных микроструктур, напоминающих выпуклые полые многогранники. Позднее, в следующих публикациях, такие микроструктуры они назвали витритами (рис. 3). В них вершинами являются молекулы воды, роль ребер играют водородные связи, а угол между водородными связями — это угол между ребрами в витрите.
Однако тепловые колебания молекул воды и взаимодействия с другими молекулами, не входящими в кластер, не дают им этого сделать, отклоняя величину угла водородной связи от равновесного значения 109,47 градуса. Чтобы как-то количественно охарактеризовать этот процесс угловой деформации, Мацумото с коллегами, основываясь на своей предыдущей работе Topological building blocks of hydrogen bond network in water, опубликованной в 2007 году в Journal of Chemical Physics, выдвинули гипотезу о существовании в воде трехмерных микроструктур, напоминающих выпуклые полые многогранники. Позднее, в следующих публикациях, такие микроструктуры они назвали витритами (рис. 3). В них вершинами являются молекулы воды, роль ребер играют водородные связи, а угол между водородными связями — это угол между ребрами в витрите.
Согласно теории Мацумото, существует огромное разнообразие форм витритов, которые, как мозаичные элементы, составляют большую часть структуры воды и которые при этом равномерно заполняют весь ее объем.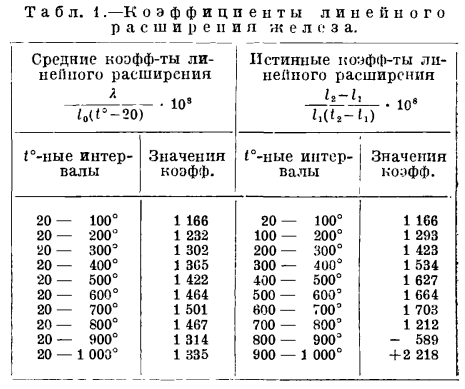
Молекулы воды стремятся создать в витритах тетраэдральные углы, поскольку витриты должны обладать минимально возможной энергией. Однако из-за тепловых движений и локальных взаимодействий с другими витритами некоторые микроструктуры не обладают геометрией с тетраэдральными углами (или углами, близкими к этому значению). Они принимают такие структурно неравновесные конфигурации (не являющиеся для них самыми выгодными с энергетической точки зрения), которые позволяют всему «семейству» витритов в целом получить наименьшее значение энергии среди возможных. Такие витриты, то есть витриты, которые как бы приносят себя в жертву «общим энергетическим интересам», называются фрустрированными. Если у нефрустрированных витритов объем полости максимален при данной температуре, то фрустрированные витриты, напротив, обладают минимально возможным объемом.
Компьютерное моделирование, проведенное Мацумото, показало, что средний объем полостей витритов с ростом температуры линейным образом уменьшается. При этом фрустрированные витриты значительно уменьшают свой объем, тогда как объем полости нефрустрированных витритов почти не меняется.
При этом фрустрированные витриты значительно уменьшают свой объем, тогда как объем полости нефрустрированных витритов почти не меняется.
Итак, сжатие воды при увеличении температуры вызвано двумя конкурирующими эффектами — удлинением водородных связей, которое приводит к увеличению объема воды, и уменьшением объема полостей фрустрированных витритов. На температурном отрезке от от 0 до 4°C последнее явление, как показали расчеты, преобладает, что в итоге и приводит к наблюдаемому сжатию воды при повышении температуры.
Осталось дождаться экспериментального подтверждения существования витритов и такого их поведения. Но это, увы, очень непростая задача.
Источник: Masakazu Matsumoto. Why Does Water Expand When It Cools? // Phys. Rev. Lett. 103, 017801 (2009).
Юрий Ерин
объемный (кубический) тепловой расширение
Удельный объем блока может быть выражен как
V = 1 / ρ = V / M (1)
, где
V = Специальный объем (M 3 /кг, FT 3 /LB)
ρ = плотность (кг /м 3 , фунт /FT 3 ) 9009, фунт /фт 3 )
V = объем блока (M 3 , FT 3 )
M = масса единицы (кг, фунт)
. Изменения могут быть выражены как
Изменения могут быть выражены как
DV = V 0 β (T 1 – T 0 ) (2)
, где
DV = V 1 .0064 – V 0 = change in volume (m 3 , ft 3 )
β = volumetric temperature expansion coefficient (m 3 /m 3 o C, ft 3 /FT 3 O F)
T 1 = Конечная температура ( O C, O F)
T 0 = Trath или С, O F)
Плотность жидкости при изменении температуры может быть выражена как
ρ 1 = M / V 0 (1 + β (T 1 -T 0 (1 + β (T 1 -T 0 0 ))
= ρ 0 / (1 + β (T 1 – T 0 )) (3)
, где
ρ 1
= Финал
ρ 1
ρ 1= Финал
= Финал
ρ 1= Финал
ρ 1
= Финал
.
(кг/м 3 , фунт/фут 3 )
ρ 0 = начальная плотность (кг/м 3 , фунт/фут 3 ) 999 9008 99 999 77777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777 Калькулятор расширения — коэффициент расширения и температура
Имейте в виду, что коэффициент расширения для некоторых жидкостей, таких как вода, может меняться в зависимости от температуры. Приведенный ниже калькулятор является универсальным и может использоваться для метрических и имперских единиц при условии, что единицы используются последовательно.
V 0 – начальный объем (M 3 , FT 3 , галлоны ..)
β – Коэффициент повышения температуры объемного )
T 0 – Начальная температура ( O C, O F )
T 1 – окончательный Ф )
- Сделать ярлык для этого калькулятора на главном экране?
Обратите внимание, , что коэффициент объемного расширения, используемый в калькуляторе, является постоянным.
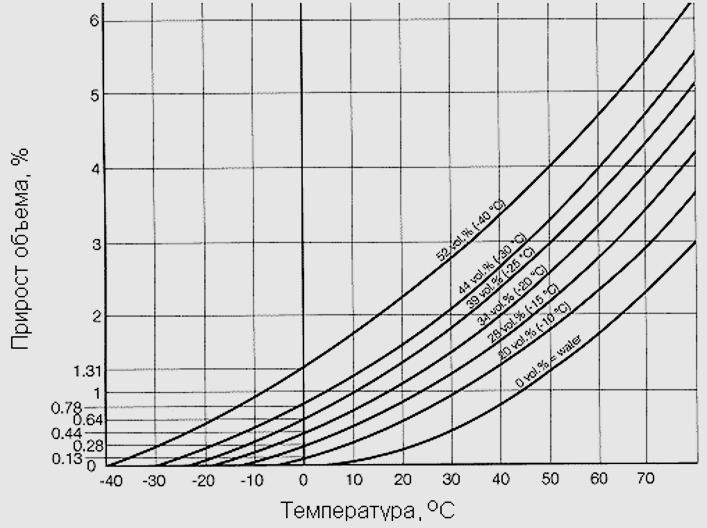
Если вы хотите рассчитать объемное изменение жидкости в диапазоне температур, в котором коэффициент объемного расширения жидкости сильно меняется, интерполируйте значения коэффициента или разделите расчет для разных температурных диапазонов. Пример – вода – это жидкость, коэффициент объемного расширения которой сильно меняется в зависимости от температуры. Вода имеет наибольшую плотность и наименьший объем при 4 или C (39.2 или F) . Объемный коэффициент для воды отрицателен ниже 4 o C и показывает, что объем a уменьшается при изменении температуры от 0 o C ( 32 o F ) до 4 o C .
Онлайн-калькулятор теплового кубического расширения — плотности
Этот калькулятор можно использовать для расчета объема расширения, когда известны начальный объем, начальная и конечная плотности жидкости
V 0 – initial volume (m 3 , ft 3 )
ρ 0 – initial density (kg/m 3 , lb/ft 3 )
ρ 1 – Конечная плотность (кг/м 3 , фунт/фут 3 )
. 3
- УДАРИЯ
- ПЛОНА ГЛАВНАЯ ГЛИЦА ГЛИНКА GLYCOL GLYCOL GLYCOL GLYCOL GLYCOL COLCOLCOLCOLE
- .
– β – for some Fluids
- water at 0 o C : -0.00005 0 (1/ o C)
- water at 4 o C : 0 (1/ O C)
- Вода при 10 O C : 0,000088 (1/ O C)
- WATER AT 20
8.01111118.0008........9008.
.....9008..9008.. .
8
8.
7- . 1/ o C)
- вода на 30 o C : 0.000303 (1/ o C)
- water at 40 o C : 0.000385 (1/ o C)
- water at 50 o C : 0.000457 (1/ o C)
- water at 60 o C : 0.000522 (1/ o C)
- water at 70 или C : 0,000582 (1/ O C)
- Вода при 80 O C : 0,000640 (1/ O C)
- WATER на
- .
O C)
- Этиловый спирт: 0,00109 (1/ O C), 0,00061 (1/ O F)
- 66: O F)
- 666: 0,0018 0,0018: . . . . . . . . . . . . С), 0,00039 (1/ или F)
- Volumetric expansion coefficients for commonly used liquids
Convert between Metric and Imperial Volumentric Temperature Coefficients
- 1 (1/ o C) = 0.56 (1/ o F)
- 1 ( 1/ O F) = 1,8 (1/ O C)
Пример – Кубическое расширение масла
100 литров – 0,1 M
2 – 0.1003100 литров –
. коэффициент объемного расширения 0,00070 1/ o C нагревается от 20 o C до 40 o C .
Объемное расширение можно рассчитать по уравнению (2)
dV = (0,1 м 3 ) (0,00070 1/ o C) ((40 o C) – (180 90 ))
= 0,0014 M 3
= 1,4 литра
Окончательный объем составляет
100 литров + 1,4 литра = 101,4 литра 0257
Пример – Объемное расширение масла
30 галлонов США масла нагревается от 7 0 o F до 100 o F . Объемное расширение можно рассчитать с помощью уравнения (2)
dV = (30 галлонов) (0,00039 1/ o F) ((100 o F) – (70 o F))
= 0,351 галлона
Конечный объем
30 галлонов + 0,351 галлона = 30,351 галлона
13.2 Тепловое расширение твердых тел и жидкостей – College Physics: OpenStax
Глава 13 Температура, кинетическая теория и законы газов
3333Резюме
Рис. 1. Термокомпенсаторы , подобные этим, на мосту через гавань Окленда в Новой Зеландии позволяют изменять длину мостов без потери устойчивости. (кредит: Ingolfson, Wikimedia Commons)
- Дайте определение и опишите тепловое расширение.
- Рассчитайте линейное расширение объекта, зная его начальную длину, изменение температуры и коэффициент линейного расширения.
- Рассчитайте объемное расширение объекта, зная его начальный объем, изменение температуры и коэффициент объемного расширения.
- Рассчитайте термическое напряжение на объекте, зная его первоначальный объем, изменение температуры, изменение объема и объемный модуль.
Расширение спирта в термометре является одним из многих часто встречающихся примеров теплового расширения , изменения размера или объема данной массы в зависимости от температуры. Горячий воздух поднимается вверх, потому что его объем увеличивается, что приводит к тому, что плотность горячего воздуха становится меньше, чем плотность окружающего воздуха, вызывая выталкивающую (поднимающую) силу на горячий воздух.
То же самое происходит со всеми жидкостями и газами, приводя к естественному переносу тепла вверх в домах, океанах и погодных системах. Твердые тела также подвергаются термическому расширению. Железнодорожные пути и мосты, например, имеют компенсаторы, что позволяет им свободно расширяться и сжиматься при изменении температуры.
Каковы основные свойства теплового расширения? Во-первых, тепловое расширение явно связано с изменением температуры. Чем больше изменение температуры, тем больше будет изгибаться биметаллическая полоса. Во-вторых, это зависит от материала. В термометре, например, расширение спирта намного больше, чем расширение стакана, содержащего его.
Какова основная причина теплового расширения? Как обсуждается в главе 13.4 «Кинетическая теория: атомное и молекулярное объяснение давления и температуры», повышение температуры подразумевает увеличение кинетической энергии отдельных атомов. В твердом теле, в отличие от газа, атомы или молекулы плотно упакованы вместе, но их кинетическая энергия (в виде небольших быстрых колебаний) отталкивает соседние атомы или молекулы друг от друга.
Это отталкивание соседа к соседу приводит в среднем к несколько большему расстоянию между соседями и в сумме к большему размеру всего тела. Для большинства веществ в обычных условиях нет предпочтительного направления, и повышение температуры увеличивает размер твердого тела на определенную долю в каждом измерении.
ЛИНЕЙНОЕ ТЕПЛОВОЕ РАСШИРЕНИЕ — ТЕПЛОВОЕ РАСШИРЕНИЕ В ОДНОМ ИЗМЕРЕНИИ
Изменение длины[латекс]\boldsymbol{\Delta{L}}[/latex]пропорционально длине[латекс]\boldsymbol{L}.[/latex]The зависимость теплового расширения от температуры, вещества и длины сводится к уравнению
[латекс]\boldsymbol{\Delta{L}=\alpha{L}\Delta{T}},[/latex]
, где[ латекс]\boldsymbol{\Delta{L}}[/latex]является изменением длины[латекс]\boldsymbol{L},\:\boldsymbol{\Delta{T}}[/latex]является изменением температуры, а [латекс]\жирныйсимвол{\альфа}[/латекс] — коэффициент линейного расширения, который незначительно зависит от температуры. 9{\circ}\textbf{C}}[/latex]или 1/К. Поскольку размер кельвина и градуса Цельсия одинаковы, как [latex]\boldsymbol{\alpha}[/latex], так и [latex]\boldsymbol{\Delta{T}}[/latex] могут быть выражены в единицах кельвинов или градусов Цельсия.
Уравнение[латекс]\жирныйсимвол{\Delta{L}=\alpha{L}\Delta{T}}[/latex] является точным для небольших изменений температуры и может использоваться для больших изменений температуры, если среднее значение [латекс]\boldsymbol{\alpha}[/латекс] используется.
Материал 9{\circ}\textbf{C}}.[/latex]Каково изменение его длины между этими температурами? Предположим, что мост сделан полностью из стали. Стратегия
Используйте уравнение линейного теплового расширения[латекс]\boldsymbol{\Delta{L}=\alpha{L}\Delta{T}}[/latex]для расчета изменения длины,[латекс] ]\boldsymbol{\Delta{L}}.[/latex]Используйте коэффициент линейного расширения,[латекс]\boldsymbol{\alpha},[/латекс]для стали из Таблицы 2, и обратите внимание, что изменение температуры, [латекс]\boldsymbol{\Delta{T}},[/latex]является[латекс]\boldsymbol{55^{\circ}\textbf{C}}.
[/latex] 9{\circ}\textbf{C})=0,84\textbf{ м.}}[/latex]
Обсуждение
Хотя это изменение длины невелико по сравнению с длиной моста, оно заметно. Обычно он распространяется на множество компенсационных швов, так что расширение в каждом шве невелико.
Объекты расширяются во всех измерениях, как показано на рисунке 2. То есть их площади и объемы, а также их длины увеличиваются с температурой. Отверстия также увеличиваются с температурой. Если вы прорежете отверстие в металлической пластине, оставшийся материал расширится точно так же, как если бы заглушка оставалась на месте. Пробка станет больше, а значит и отверстие тоже должно стать больше. (Представьте, что кольцо соседних атомов или молекул на стенке отверстия отталкивает друг друга все дальше друг от друга по мере повышения температуры. Очевидно, что кольцо соседей должно немного увеличиваться, поэтому отверстие становится немного больше).
ТЕПЛОВОЕ РАСШИРЕНИЕ В ДВУХ ИЗМЕРЕНИЯХ
При небольших изменениях температуры изменение площади [латекс]\boldsymbol{\Delta{A}}[/latex] определяется выражением
[латекс]\boldsymbol{\Delta{A}= 2\alpha{A}\Delta{T}},[/latex]
, где[latex]\boldsymbol{\Delta{A}}[/latex]изменение площади[latex]\boldsymbol{A}, \:\boldsymbol{\Delta{T}}[/latex] – изменение температуры, а [latex]\boldsymbol{\alpha}[/latex] – коэффициент линейного расширения, который незначительно зависит от температуры.
Рисунок 2. Обычно объекты расширяются во всех направлениях при повышении температуры. На этих рисунках исходные границы объектов показаны сплошными линиями, а расширенные границы — пунктирными линиями. а) Площадь увеличивается, потому что увеличиваются и длина, и ширина. Площадь круглой пробки также увеличивается. (b) Если заглушка удалена, отверстие, которое она оставляет, становится больше с повышением температуры, как если бы расширяющаяся заглушка оставалась на месте. в) Объем также увеличивается, потому что увеличиваются все три измерения.ТЕПЛОВОЕ РАСШИРЕНИЕ В ТРЕХ ИЗМЕРЕНИЯХ
Изменение объема [латекс]\boldsymbol{\Delta{V}}[/latex]очень близко к [латексу]\boldsymbol{\Delta{V}=3\alpha{V}\ Delta{T}}.[/latex]Это уравнение обычно записывается как
[латекс]\boldsymbol{\Delta{V}=\beta{V}\Delta{T}},[/latex]
, где[ латекс]\boldsymbol{\beta}[/latex]– коэффициент объемного расширения, а [латекс]\boldsymbol{\beta\приблизительно{3}\альфа}.
Рис. 3. Плотность воды как функция температуры. Обратите внимание, что тепловое расширение на самом деле очень мало. Максимальная плотность при +4 0 C всего на 0,0075% больше, чем при 2°C , и на 0,012% больше, чем при 0°C .[/latex]Обратите внимание, что значения [латекс]\boldsymbol {\beta}[/latex]в таблице 2 почти точно равны[latex]\boldsymbol{3\alpha}.[/latex] 9{\circ}\textbf{C}}[/latex] вода подо льдом из-за этой необычной характеристики воды. Он также производит циркуляцию воды в пруду, что необходимо для здоровой экосистемы водоема.
ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ: РЕАЛЬНЫЕ СОЕДИНЕНИЯ — ЗАПОЛНЕНИЕ БАКА
Различия в тепловом расширении материалов могут привести к интересным эффектам на заправочной станции. Одним из примеров является капание бензина из только что заправленного бака в жаркий день. Бензин стартует при температуре земли под заправкой, которая ниже температуры воздуха над ней.
Бензин охлаждает стальной бак, когда он заполнен. И бензин, и стальной бак расширяются при нагревании до температуры воздуха, но бензин расширяется гораздо больше, чем сталь, поэтому он может перелиться через край.
Эта разница в расширении также может вызвать проблемы при интерпретации показаний указателя уровня бензина. Фактическое количество (масса) бензина, оставшегося в баке, когда датчик показывает «пусто», летом намного меньше, чем зимой. Бензин имеет тот же объем, что и зимой, когда загорается индикатор «добавьте топливо», но из-за того, что бензин расширился, масса стала меньше. Если вы привыкли проезжать еще 40 миль «пустым» зимой, будьте осторожны — летом вы, вероятно, выбежите гораздо быстрее. 9{\circ}\textbf{C}}?[/latex]
Стратегия
Бак и бензин увеличиваются в объеме, но бензин увеличивается больше, поэтому количество пролитого равно разнице в изменении их объема. (Бензиновый бак можно рассматривать как твердую сталь.) Мы можем использовать уравнение для расширения объема, чтобы вычислить изменение объема бензина и бака.
Решение
1. Используйте уравнение для объемного расширения, чтобы рассчитать увеличение объема стального резервуара:
[латекс] \boldsymbol{\Delta{V}_{\textbf{s}}=\beta_{\textbf{s}}V_{\textbf{s}}\Delta{T}}.[/latex]
2. Увеличение объема бензина определяется следующим уравнением: \textbf{gas}}\Delta{T}}.[/latex]
3. Найдите разницу в объеме, чтобы определить количество пролитого вещества как
[латекс]\boldsymbol{V _{\textbf{spill}}=\ Delta{V}_{\textbf{gas}}-\Delta{V}_{\textbf{s}}}.[/latex]
В качестве альтернативы мы можем объединить эти три уравнения в одно уравнение. (Обратите внимание, что исходные объемы равны.) 9{\circ}\textbf{C})} \\ {} & \boldsymbol{=} & \boldsymbol{1.10\textbf{L.}} \end{array}[/latex]
Обсуждение
Это количество является значительным, особенно для бака на 60,0 л. Эффект настолько поразителен, потому что бензин и сталь быстро расширяются. Скорость изменения термических свойств обсуждается в главе 14 «Тепло и методы теплопередачи».
Если вы попытаетесь плотно закрыть бак, чтобы предотвратить переполнение, вы обнаружите, что он все равно протекает, либо вокруг крышки, либо из-за разрыва бака. Плотное сжатие расширяющегося газа эквивалентно его сжатию, а как жидкости, так и твердые тела сопротивляются сжатию с чрезвычайно большими силами. Чтобы избежать разрыва жестких контейнеров, эти контейнеры имеют воздушные зазоры, которые позволяют им расширяться и сжиматься, не нагружая их.
Термическое напряжение создается тепловым расширением или сжатием (см. главу 5.3 Эластичность: напряжение и деформация для обсуждения напряжения и деформации). Термическое напряжение может быть разрушительным, например, когда расширяющийся бензин разрывает бак. Это также может быть полезно, например, когда две детали соединяются вместе путем нагревания одной в процессе производства, затем надевания ее на другую и охлаждения комбинации. Термический стресс может объяснить многие явления, такие как выветривание горных пород и дорожного покрытия из-за расширения льда при замерзании.
92}.[/latex](Дополнительные сведения о объемном модуле см. в главе 5.3 «Упругость: напряжение и деформация».) латекс]\boldsymbol{\Delta{V}}[/latex]к давлению:
[латекс]\boldsymbol{\Delta{V}\:=}[/latex][латекс]\boldsymbol{\frac{1} {B}\frac{F}{A}}[/latex][latex]\boldsymbol{V_0,}[/latex]
, где[latex]\boldsymbol{F/A}[/latex] — давление,[ латекс]\boldsymbol{V_0}[/latex]– первоначальный объем, а [латекс]\boldsymbol{B}[/latex]– модуль объемного сжатия используемого материала. Мы будем использовать количество, пролитое в Примере 2, как изменение объема,[латекс]\жирныйсимвол{\Delta{V}}.[/латекс] 92},[/latex] гораздо больше, чем может выдержать бензобак.
Силы и давления, создаваемые термическим напряжением, обычно такие же большие, как и в приведенном выше примере. Железнодорожные пути и проезжие части могут деформироваться в жаркие дни, если на них недостаточно компенсационных швов. (См. рис. 5.) Линии электропередач провисают больше летом, чем зимой, и ломаются в холодную погоду, если провисание недостаточное.
Рис. 5. Термическое напряжение способствует образованию выбоин. (кредит: Editor5807, Wikimedia Commons)Трещины в оштукатуренных стенах открываются и закрываются по мере того, как дом нагревается и остывает. Стеклянные кастрюли треснут при быстром или неравномерном охлаждении из-за дифференциального сжатия и создаваемых им напряжений. (Pyrex® менее чувствителен из-за его низкого коэффициента теплового расширения.) Корпусам высокого давления ядерных реакторов угрожает чрезмерно быстрое охлаждение, и, хотя ни один из них не вышел из строя, некоторые охлаждались быстрее, чем считалось желательным. Биологические клетки разрушаются при замораживании продуктов, что ухудшает их вкус. Многократное оттаивание и замораживание усугубляют ущерб. Даже океаны могут быть затронуты. Значительная часть повышения уровня моря в результате глобального потепления связана с тепловым расширением морской воды.
Металл регулярно используется в человеческом теле для имплантатов бедра и колена.
Большинство имплантатов со временем необходимо заменять, потому что, среди прочего, металл не сцепляется с костью. Исследователи пытаются найти лучшие металлические покрытия, которые позволили бы связывать металл с костью. Одна из задач состоит в том, чтобы найти покрытие с коэффициентом расширения, аналогичным коэффициенту расширения металла. Если коэффициенты расширения слишком разные, термические напряжения в процессе производства приводят к трещинам на границе раздела покрытие-металл.
Еще один пример термического стресса обнаружен во рту. Зубные пломбы могут расширяться иначе, чем зубная эмаль. Это может вызывать боль при употреблении мороженого или горячего напитка. В пломбе могут появиться трещины. Металлические пломбы (золото, серебро и др.) вытесняются композитными пломбами (фарфор), имеющими меньшие коэффициенты расширения и более близкие к зубным.
- Тепловое расширение — это увеличение или уменьшение размера (длины, площади или объема) тела из-за изменения температуры.
- Тепловое расширение велико для газов и относительно мало, но им можно пренебречь, для жидкостей и твердых тел.
- Линейное тепловое расширение
[латекс]\boldsymbol{\Delta{L}=\alpha{L}\Delta{T}},[/latex]
, где [латекс]\boldsymbol{\Delta{L}}[/latex]— изменение длины[латекс]\boldsymbol{L}, \:\boldsymbol{\Delta{T}}[/latex]— изменение зависит от температуры, а [латекс]\boldsymbol{\alpha}[/латекс] — коэффициент линейного расширения, который незначительно зависит от температуры.
- Изменение площади из-за теплового расширения составляет
[латекс]\boldsymbol{\Delta{A}=2\alpha{A}\Delta{T}},[/latex]
, где[латекс]\жирныйсимвол{\Дельта{А}}[/латекс] — изменение площади.
- Изменение объема из-за теплового расширения
[латекс]\boldsymbol{\Delta{V}=\beta{V}\Delta{T}},[/latex]
, где[латекс]\жирныйсимвол{\бета}[/латекс]является коэффициентом объемного расширения, а[латекс]\жирныйсимвол{\бета\приблизительно3\альфа}.[/латекс]Термическое напряжение создается, когда тепловое расширение ограничено.
 (кг/м 3 , фунт/фут 3 )
(кг/м 3 , фунт/фут 3 )  Если вы хотите рассчитать объемное изменение жидкости в диапазоне температур, в котором коэффициент объемного расширения жидкости сильно меняется, интерполируйте значения коэффициента или разделите расчет для разных температурных диапазонов. Пример – вода – это жидкость, коэффициент объемного расширения которой сильно меняется в зависимости от температуры. Вода имеет наибольшую плотность и наименьший объем при 4 или C (39.2 или F) . Объемный коэффициент для воды отрицателен ниже 4 o C и показывает, что объем a уменьшается при изменении температуры от 0 o C ( 32 o F ) до 4 o C .
Если вы хотите рассчитать объемное изменение жидкости в диапазоне температур, в котором коэффициент объемного расширения жидкости сильно меняется, интерполируйте значения коэффициента или разделите расчет для разных температурных диапазонов. Пример – вода – это жидкость, коэффициент объемного расширения которой сильно меняется в зависимости от температуры. Вода имеет наибольшую плотность и наименьший объем при 4 или C (39.2 или F) . Объемный коэффициент для воды отрицателен ниже 4 o C и показывает, что объем a уменьшается при изменении температуры от 0 o C ( 32 o F ) до 4 o C . – β – for some Fluids
– β – for some Fluids  O C)
O C)  Объемное расширение можно рассчитать по уравнению (2)
Объемное расширение можно рассчитать по уравнению (2) 
 То же самое происходит со всеми жидкостями и газами, приводя к естественному переносу тепла вверх в домах, океанах и погодных системах. Твердые тела также подвергаются термическому расширению. Железнодорожные пути и мосты, например, имеют компенсаторы, что позволяет им свободно расширяться и сжиматься при изменении температуры.
То же самое происходит со всеми жидкостями и газами, приводя к естественному переносу тепла вверх в домах, океанах и погодных системах. Твердые тела также подвергаются термическому расширению. Железнодорожные пути и мосты, например, имеют компенсаторы, что позволяет им свободно расширяться и сжиматься при изменении температуры. Это отталкивание соседа к соседу приводит в среднем к несколько большему расстоянию между соседями и в сумме к большему размеру всего тела. Для большинства веществ в обычных условиях нет предпочтительного направления, и повышение температуры увеличивает размер твердого тела на определенную долю в каждом измерении.
Это отталкивание соседа к соседу приводит в среднем к несколько большему расстоянию между соседями и в сумме к большему размеру всего тела. Для большинства веществ в обычных условиях нет предпочтительного направления, и повышение температуры увеличивает размер твердого тела на определенную долю в каждом измерении. Уравнение[латекс]\жирныйсимвол{\Delta{L}=\alpha{L}\Delta{T}}[/latex] является точным для небольших изменений температуры и может использоваться для больших изменений температуры, если среднее значение [латекс]\boldsymbol{\alpha}[/латекс] используется.
Уравнение[латекс]\жирныйсимвол{\Delta{L}=\alpha{L}\Delta{T}}[/latex] является точным для небольших изменений температуры и может использоваться для больших изменений температуры, если среднее значение [латекс]\boldsymbol{\alpha}[/латекс] используется. [/latex] 9{\circ}\textbf{C})=0,84\textbf{ м.}}[/latex]
[/latex] 9{\circ}\textbf{C})=0,84\textbf{ м.}}[/latex]
 [/latex]Обратите внимание, что значения [латекс]\boldsymbol {\beta}[/latex]в таблице 2 почти точно равны[latex]\boldsymbol{3\alpha}.[/latex] 9{\circ}\textbf{C}}[/latex] вода подо льдом из-за этой необычной характеристики воды. Он также производит циркуляцию воды в пруду, что необходимо для здоровой экосистемы водоема.
[/latex]Обратите внимание, что значения [латекс]\boldsymbol {\beta}[/latex]в таблице 2 почти точно равны[latex]\boldsymbol{3\alpha}.[/latex] 9{\circ}\textbf{C}}[/latex] вода подо льдом из-за этой необычной характеристики воды. Он также производит циркуляцию воды в пруду, что необходимо для здоровой экосистемы водоема.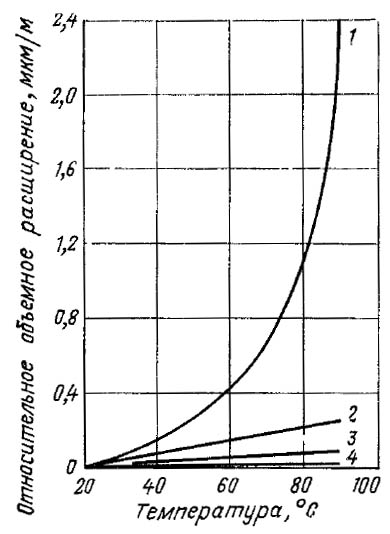 Бензин охлаждает стальной бак, когда он заполнен. И бензин, и стальной бак расширяются при нагревании до температуры воздуха, но бензин расширяется гораздо больше, чем сталь, поэтому он может перелиться через край.
Бензин охлаждает стальной бак, когда он заполнен. И бензин, и стальной бак расширяются при нагревании до температуры воздуха, но бензин расширяется гораздо больше, чем сталь, поэтому он может перелиться через край.
 92}.[/latex](Дополнительные сведения о объемном модуле см. в главе 5.3 «Упругость: напряжение и деформация».) латекс]\boldsymbol{\Delta{V}}[/latex]к давлению:
92}.[/latex](Дополнительные сведения о объемном модуле см. в главе 5.3 «Упругость: напряжение и деформация».) латекс]\boldsymbol{\Delta{V}}[/latex]к давлению: Трещины в оштукатуренных стенах открываются и закрываются по мере того, как дом нагревается и остывает. Стеклянные кастрюли треснут при быстром или неравномерном охлаждении из-за дифференциального сжатия и создаваемых им напряжений. (Pyrex® менее чувствителен из-за его низкого коэффициента теплового расширения.) Корпусам высокого давления ядерных реакторов угрожает чрезмерно быстрое охлаждение, и, хотя ни один из них не вышел из строя, некоторые охлаждались быстрее, чем считалось желательным. Биологические клетки разрушаются при замораживании продуктов, что ухудшает их вкус. Многократное оттаивание и замораживание усугубляют ущерб. Даже океаны могут быть затронуты. Значительная часть повышения уровня моря в результате глобального потепления связана с тепловым расширением морской воды.
Трещины в оштукатуренных стенах открываются и закрываются по мере того, как дом нагревается и остывает. Стеклянные кастрюли треснут при быстром или неравномерном охлаждении из-за дифференциального сжатия и создаваемых им напряжений. (Pyrex® менее чувствителен из-за его низкого коэффициента теплового расширения.) Корпусам высокого давления ядерных реакторов угрожает чрезмерно быстрое охлаждение, и, хотя ни один из них не вышел из строя, некоторые охлаждались быстрее, чем считалось желательным. Биологические клетки разрушаются при замораживании продуктов, что ухудшает их вкус. Многократное оттаивание и замораживание усугубляют ущерб. Даже океаны могут быть затронуты. Значительная часть повышения уровня моря в результате глобального потепления связана с тепловым расширением морской воды. 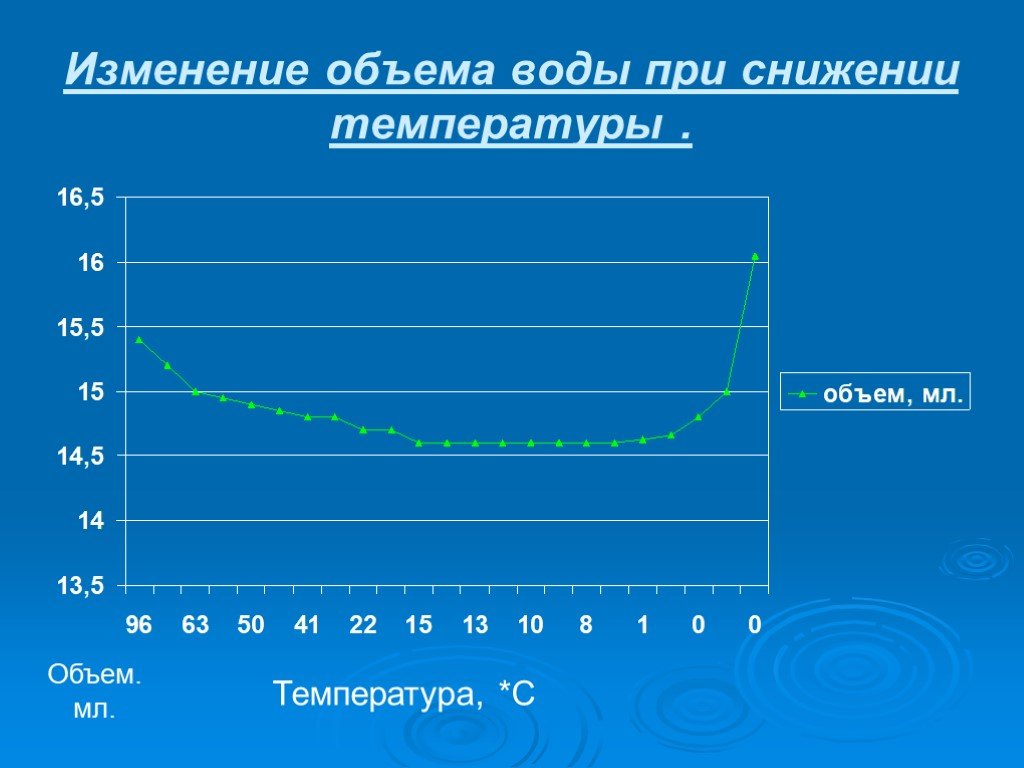 Большинство имплантатов со временем необходимо заменять, потому что, среди прочего, металл не сцепляется с костью. Исследователи пытаются найти лучшие металлические покрытия, которые позволили бы связывать металл с костью. Одна из задач состоит в том, чтобы найти покрытие с коэффициентом расширения, аналогичным коэффициенту расширения металла. Если коэффициенты расширения слишком разные, термические напряжения в процессе производства приводят к трещинам на границе раздела покрытие-металл.
Большинство имплантатов со временем необходимо заменять, потому что, среди прочего, металл не сцепляется с костью. Исследователи пытаются найти лучшие металлические покрытия, которые позволили бы связывать металл с костью. Одна из задач состоит в том, чтобы найти покрытие с коэффициентом расширения, аналогичным коэффициенту расширения металла. Если коэффициенты расширения слишком разные, термические напряжения в процессе производства приводят к трещинам на границе раздела покрытие-металл.