Предложена новая теория, объясняющая, почему вода при нагревании от 0 до 4°C сжимается • Юрий Ерин • Новости науки на «Элементах» • Физика
Японский физик Масакадзу Мацумото выдвинул теорию, которая объясняет, почему вода при нагревании от 0 до 4°C сжимается, вместо того чтобы расширяться. Согласно его модели, вода содержит микрообразования — «витриты», представляющие собой выпуклые пустотелые многогранники, в вершинах которых находятся молекулы воды, а ребрами служат водородные связи. При повышении температуры конкурируют между собой два явления: удлинение водородных связей между молекулами воды и деформация витритов, приводящая к уменьшению их полостей. В диапазоне температур от 0 до 3,98°C последнее явление доминирует над эффектом удлинения водородных связей, что в итоге и дает наблюдаемое сжатие воды. Экспериментального подтверждения модели Мацумото пока что нет — впрочем, как и других теорий, объясняющих сжатие воды.
В отличие от подавляющего большинства веществ, вода при нагревании способна уменьшать свой объем (рис.
1), то есть обладает отрицательным коэффициентом теплового расширения. Впрочем, речь идет не обо всём температурном интервале, где вода существует в жидком состоянии, а лишь об узком участке — от 0°C примерно до 4°C. При больших температурах вода, как и другие вещества, расширяется.
Между прочим, вода — не единственное вещество, имеющее свойство сжиматься при увеличении температуры (или расширяться при охлаждении). Подобным поведением могут «похвастать» еще висмут, галлий, кремний и сурьма. Тем не менее, в силу своей более сложной внутренней структуры, а также распространенности и важности в разнообразных процессах, именно вода приковывает внимание ученых (см. Продолжается изучение структуры воды, «Элементы», 09.10.2006).
Некоторое время назад общепринятой теорией, отвечающей на вопрос, почему вода увеличивает свой объем при понижении температуры (рис. 1), была модель смеси двух компонент — «нормальной» и «льдоподобной». Впервые эта теория была предложена в XIX веке Гарольдом Витингом и позднее была развита и усовершенствована многими учеными.
Сравнительно недавно в рамках обнаруженного полиморфизма воды теория Витинга была переосмыслена. Отныне считается, что в переохлажденной воде существует два типа льдообразных нанодоменов: области, похожие на аморфный лед высокой и низкой плотности. Нагревание переохлажденной воды приводит к плавлению этих наноструктур и к появлению двух видов воды: с большей и меньшей плотностью. Хитрая температурная конкуренция между двумя «сортами» образовавшейся воды и порождает немонотонную зависимость плотности от температуры. Однако пока эта теория не подтверждена экспериментально.
С приведенным объяснением нужно быть осторожным. Не случайно здесь говорится лишь о структурах, которые напоминают аморфный лед. Дело в том, что наноскопические области аморфного льда и его макроскопические аналоги обладают разными физическими параметрами.
Японский физик Масакадзу Мацумото решил найти объяснение обсуждаемого здесь эффекта «с нуля», отбросив теорию двухкомпонентной смеси. Используя компьютерное моделирование, он рассмотрел физические свойства воды в широком диапазоне температур — от 200 до 360 К при нулевом давлении, чтобы в молекулярном масштабе выяснить истинные причины расширения воды при ее охлаждении.
Его статья в журнале Physical Review Letters так и называется: Why Does Water Expand When It Cools? («Почему вода при охлаждении расширяется?»).
Изначально автор статьи задался вопросом: что влияет на коэффициент теплового расширения воды? Мацумото считает, что для этого достаточно выяснить влияние всего трех факторов: 1) изменения длины водородных связей между молекулами воды, 2) топологического индекса — числа связей на одну молекулу воды и 3) отклонения величины угла между связями от равновесного значения (углового искажения).
Перед тем как рассказать о результатах, полученных японским физиком, сделаем важные замечания и разъяснения по поводу вышеупомянутых трех факторов. Прежде всего, привычная химическая формула воды H2O соответствует лишь парообразному ее состоянию. В жидкой форме молекулы воды посредством водородной связи объединяются в группы (H2O)x, где x — количество молекул. Наиболее энергетически выгодно объединение из пяти молекул воды (x = 5) с четырьмя водородными связями, в котором связи образуют равновесный, так называемый тетраэдральный угол, равный 109,47 градуса (см.
рис. 2).
Проанализировав зависимость длины водородной связи между молекулами воды от температуры, Мацумото пришел к ожидаемому выводу: рост температуры рождает линейное удлинение водородных связей. А это, в свою очередь, приводит к увеличению объема воды, то есть к ее расширению. Сей факт противоречит наблюдаемым результатам, поэтому далее он рассмотрел влияние второго фактора. Как коэффициент теплового расширения зависит от топологического индекса?
Компьютерное моделирование дало следующий результат. При низких температурах наибольший объем воды в процентном отношении занимают кластеры воды, у которых на одну молекулу приходится 4 водородных связи (топологический индекс равен 4). Повышение температуры вызывает уменьшение количества ассоциатов с индексом 4, но при этом начинает возрастать число кластеров с индексами 3 и 5. Проведя численные расчеты, Мацумото обнаружил, что локальный объем кластеров с топологическим индексом 4 с повышением температуры практически не меняется, а изменение суммарного объема ассоциатов с индексами 3 и 5 при любой температуре взаимно компенсирует друг друга.
Следовательно, изменение температуры не меняет общий объем воды, а значит, и топологический индекс никакого воздействия на сжатие воды при ее нагревании не оказывает.
Остается выяснить влияние углового искажения водородных связей. И вот здесь начинается самое интересное и важное. Как было сказано выше, молекулы воды стремятся объединиться так, чтобы угол между водородными связями был тетраэдральным. Однако тепловые колебания молекул воды и взаимодействия с другими молекулами, не входящими в кластер, не дают им этого сделать, отклоняя величину угла водородной связи от равновесного значения 109,47 градуса. Чтобы как-то количественно охарактеризовать этот процесс угловой деформации, Мацумото с коллегами, основываясь на своей предыдущей работе Topological building blocks of hydrogen bond network in water, опубликованной в 2007 году в Journal of Chemical Physics, выдвинули гипотезу о существовании в воде трехмерных микроструктур, напоминающих выпуклые полые многогранники. Позднее, в следующих публикациях, такие микроструктуры они назвали витритами (рис.
3). В них вершинами являются молекулы воды, роль ребер играют водородные связи, а угол между водородными связями — это угол между ребрами в витрите.
Согласно теории Мацумото, существует огромное разнообразие форм витритов, которые, как мозаичные элементы, составляют большую часть структуры воды и которые при этом равномерно заполняют весь ее объем.
Молекулы воды стремятся создать в витритах тетраэдральные углы, поскольку витриты должны обладать минимально возможной энергией. Однако из-за тепловых движений и локальных взаимодействий с другими витритами некоторые микроструктуры не обладают геометрией с тетраэдральными углами (или углами, близкими к этому значению). Они принимают такие структурно неравновесные конфигурации (не являющиеся для них самыми выгодными с энергетической точки зрения), которые позволяют всему «семейству» витритов в целом получить наименьшее значение энергии среди возможных. Такие витриты, то есть витриты, которые как бы приносят себя в жертву «общим энергетическим интересам», называются фрустрированными.
Если у нефрустрированных витритов объем полости максимален при данной температуре, то фрустрированные витриты, напротив, обладают минимально возможным объемом.
Компьютерное моделирование, проведенное Мацумото, показало, что средний объем полостей витритов с ростом температуры линейным образом уменьшается. При этом фрустрированные витриты значительно уменьшают свой объем, тогда как объем полости нефрустрированных витритов почти не меняется.
Итак, сжатие воды при увеличении температуры вызвано двумя конкурирующими эффектами — удлинением водородных связей, которое приводит к увеличению объема воды, и уменьшением объема полостей фрустрированных витритов. На температурном отрезке от от 0 до 4°C последнее явление, как показали расчеты, преобладает, что в итоге и приводит к наблюдаемому сжатию воды при повышении температуры.
Осталось дождаться экспериментального подтверждения существования витритов и такого их поведения. Но это, увы, очень непростая задача.
Источник: Masakazu Matsumoto.
Why Does Water Expand When It Cools? // Phys. Rev. Lett. 103, 017801 (2009).
Юрий Ерин
Тепловое расширение • Джеймс Трефил, энциклопедия «Двести законов мироздания»
200 законов мироздания > Физика
Изменение линейных размеров тела при нагревании пропорционально изменению температуры.
Подавляющее большинство веществ при нагревании расширяется. Это легко объяснимо с позиции механической теории теплоты, поскольку при нагревании молекулы или атомы вещества начинают двигаться быстрее. В твердых телах атомы начинают с большей амплитудой колебаться вокруг своего среднего положения в кристаллической решетке, и им требуется больше свободного пространства. В результате тело расширяется. Так же и жидкости и газы, по большей части, расширяются с повышением температуры по причине увеличения скорости теплового движения свободных молекул (см. Закон Бойля—Мариотта, Закон Шарля, Уравнение состояния идеального газа).
Основной закон теплового расширения гласит, что тело с линейным размером L в соответствующем измерении при увеличении его температуры на ΔТ расширяется на величину ΔL, равную:
Δ
где α — так называемый коэффициент линейного теплового расширения.
Аналогичные формулы имеются для расчета изменения площади и объема тела. В приведенном простейшем случае, когда коэффициент теплового расширения не зависит ни от температуры, ни от направления расширения, вещество будет равномерно расширяться по всем направлениям в строгом соответствии с вышеприведенной формулой.
Для инженеров тепловое расширение — жизненно важное явление. Проектируя стальной мост через реку в городе с континентальным климатом, нельзя не учитывать возможного перепада температур в пределах от —40°C до +40°C в течение года. Такие перепады вызовут изменение общей длины моста вплоть до нескольких метров, и, чтобы мост не вздыбливался летом и не испытывал мощных нагрузок на разрыв зимой, проектировщики составляют мост из отдельных секций, соединяя их специальными термическими буферными сочленениями, которые представляют собой входящие в зацепление, но не соединенные жестко ряды зубьев, которые плотно смыкаются в жару и достаточно широко расходятся в стужу. На длинном мосту может насчитываться довольно много таких буферов.
Однако не все материалы, особенно это касается кристаллических твердых тел, расширяются равномерно по всем направлениям. И далеко не все материалы расширяются одинаково при разных температурах. Самый яркий пример последнего рода — вода. При охлаждении вода сначала сжимается, как и большинство веществ. Однако, начиная с +4°C и до точки замерзания 0°C вода начинает расширяться при охлаждении и сжиматься при нагревании (с точки зрения приведенной выше формулы можно сказать, что в интервале температур от 0°C до +4°C коэффициент теплового расширения воды
То, что лед имеет удельную плотность ниже плотности воды, — еще одно (хотя и не связанное с предыдущим) аномальное свойство воды, которому мы обязаны существованием жизни на нашей планете.
Если бы не этот эффект, лед шел бы ко дну рек, озер и океанов, и они, опять же, вымерзли бы до дна, убив всё живое.
1
Показать комментарии (1)
Свернуть комментарии (1)
- Свойвзгляд
07.02.2010 11:23
Ответить
Всё, что связано с теплом и холодом связано с важнейшим физическим термином и понятием – “ТЕМПЕРАТУРА”. А это самое непроработанное физическое понятие в основе которого до сих пор нет самого физического объекта (предмета) обозначаемого словом температура. Объект-теплоноситель этой самой температуры не выявлен. Какая температура у отдельной молекулы? Какие объекты дают температуру в глубоком космическом вакууме? Что является источником температуры в 1000К в ионосфере Земли? Знает ли современная физика ответы на эти вопросы? Почему энтропия вселенной сейчас возрастает? Будет ли период в развитии нашей вселенной, когда второе начало термодинамики станет своей противоположностью и энтропия начнёт падать (уменьшаться)? Если знать объект-источник “Температуры”, то и на все эти вопросы сможем ответить легко и непринуждённо.
Ответ на вопрос о причине расширения тел при нагревании найдёт своё однозначное решение. И не только тел. Даже вукуум при нагревании расширяется. Это что касается проблемы предсказания правильной теории. Если это прочитают физики эксперементаторы, то попробуйте на инструментальной основе подтвердить этот факт. Вероятность подтверждения 100%. Это будет значительный вклад в развитие физики. Ну, а уж право теоретического обоснования оставляю за собой.Ответить
Написать комментарий
около 1800 | Тепловое расширение |
XIX век
Теплообмен
1859
Теория эволюции
Новостная рассылка
«Элементы» в соцсетях:
13.2 Тепловое расширение твердых тел и жидкостей – Колледж физики: OpenStax
Глава 13 Температура, кинетическая теория и газовые законы
Резюме
- Дайте определение и опишите тепловое расширение.
- Рассчитать линейное расширение объекта, зная его начальную длину, изменение температуры и коэффициент линейного расширения.
- Рассчитать объемное расширение объекта, зная его начальный объем, изменение температуры и коэффициент объемного расширения.
- Расчет термической нагрузки на объект по его первоначальному объему, изменению температуры, изменению объема и объемному модулю.
Расширение спирта в термометре является одним из многих часто встречающихся примеров теплового расширения , изменения размера или объема данной массы в зависимости от температуры. Горячий воздух поднимается вверх, потому что его объем увеличивается, что приводит к тому, что плотность горячего воздуха становится меньше, чем плотность окружающего воздуха, вызывая выталкивающую (поднимающую) силу на горячий воздух.
Каковы основные свойства теплового расширения? Во-первых, тепловое расширение явно связано с изменением температуры. Чем больше изменение температуры, тем больше будет изгибаться биметаллическая полоса. Во-вторых, это зависит от материала. В термометре, например, расширение спирта намного больше, чем расширение стакана, содержащего его.
Какова основная причина теплового расширения? Как обсуждается в главе 13.4 «Кинетическая теория: атомное и молекулярное объяснение давления и температуры», повышение температуры подразумевает увеличение кинетической энергии отдельных атомов. В твердом теле, в отличие от газа, атомы или молекулы плотно упакованы вместе, но их кинетическая энергия (в виде небольших быстрых колебаний) отталкивает соседние атомы или молекулы друг от друга.
ЛИНЕЙНОЕ ТЕПЛОВОЕ РАСШИРЕНИЕ — ТЕПЛОВОЕ РАСШИРЕНИЕ В ОДНОМ ИЗМЕРЕНИИ
Изменение длины[латекс]\boldsymbol{\Delta{L}}[/латекс]пропорционально длине[латекс]\жирныйсимвол{L}.[/латекс] зависимость теплового расширения от температуры, вещества и длины сводится к уравнению
[латекс]\boldsymbol{\Delta{L}=\alpha{L}\Delta{T}},[/latex]
, где[ латекс]\boldsymbol{\Delta{L}}[/latex]является изменением длины[латекс]\boldsymbol{L},\:\boldsymbol{\Delta{T}}[/latex]является изменением температуры, а [латекс]\жирныйсимвол{\альфа}[/латекс] — коэффициент линейного расширения, который незначительно зависит от температуры. 9{\circ}\textbf{C}}[/latex]или 1/К. Поскольку размер кельвина и градуса Цельсия одинаковы, как [latex]\boldsymbol{\alpha}[/latex], так и [latex]\boldsymbol{\Delta{T}}[/latex] могут быть выражены в единицах кельвинов или градусов Цельсия.
Уравнение[латекс]\жирныйсимвол{\Delta{L}=\alpha{L}\Delta{T}}[/latex] является точным для небольших изменений температуры и может использоваться для больших изменений температуры, если среднее значение [латекс]\boldsymbol{\alpha}[/латекс] используется.
| Материал 9{\circ}\textbf{C}}.[/latex]Каково изменение его длины между этими температурами? Предположим, что мост сделан полностью из стали. Стратегия Используйте уравнение линейного теплового расширения[латекс]\boldsymbol{\Delta{L}=\alpha{L}\Delta{T}}[/latex]для расчета изменения длины,[латекс] ]\boldsymbol{\Delta{L}}.[/latex]Используйте коэффициент линейного расширения,[латекс]\boldsymbol{\alpha},[/латекс]для стали из Таблицы 2, и обратите внимание, что изменение температуры, [латекс]\boldsymbol{\Delta{T}},[/latex]является[латекс]\boldsymbol{55^{\circ}\textbf{C}}. Обсуждение Хотя это изменение длины невелико по сравнению с длиной моста, оно заметно. Обычно он распространяется на множество компенсационных швов, так что расширение в каждом шве невелико. Объекты расширяются во всех измерениях, как показано на рисунке 2. То есть их площади и объемы, а также их длины увеличиваются с температурой. Отверстия также увеличиваются с температурой. Если вы прорежете отверстие в металлической пластине, оставшийся материал расширится точно так же, как если бы заглушка оставалась на месте. Пробка станет больше, а значит и отверстие тоже должно стать больше. (Представьте, что кольцо соседних атомов или молекул на стенке отверстия отталкивает друг друга все дальше друг от друга по мере повышения температуры. Очевидно, что кольцо соседей должно немного увеличиваться, поэтому отверстие становится немного больше). ТЕПЛОВОЕ РАСШИРЕНИЕ В ДВУХ ИЗМЕРЕНИЯХДля небольших изменений температуры изменение площади [латекс]\boldsymbol{\Delta{A}}[/latex] определяется как [латекс]\boldsymbol{\Delta{A}= 2\alpha{A}\Delta{T}},[/latex] , где[latex]\boldsymbol{\Delta{A}}[/latex]изменение площади[latex]\boldsymbol{A}, \:\boldsymbol{\Delta{T}}[/latex] – изменение температуры, а [latex]\boldsymbol{\alpha}[/latex] – коэффициент линейного расширения, который незначительно зависит от температуры. ТЕПЛОВОЕ РАСШИРЕНИЕ В ТРЕХ ИЗМЕРЕНИЯХИзменение объема [латекс]\boldsymbol{\Delta{V}}[/latex]очень близко к [латексу]\boldsymbol{\Delta{V}=3\alpha{V}\ Delta{T}}.[/latex]Это уравнение обычно записывается как [латекс]\boldsymbol{\Delta{V}=\beta{V}\Delta{T}},[/latex] , где[ латекс]\boldsymbol{\beta}[/latex]– коэффициент объемного расширения, а [латекс]\boldsymbol{\beta\приблизительно{3}\альфа}. ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ: РЕАЛЬНЫЕ СОЕДИНЕНИЯ — ЗАПОЛНЕНИЕ БАКА Различия в тепловом расширении материалов могут привести к интересным эффектам на заправочной станции. Одним из примеров является капание бензина из только что заправленного бака в жаркий день. Бензин стартует при температуре земли под заправкой, которая ниже температуры воздуха над ней. Эта разница в расширении также может вызвать проблемы при интерпретации показаний указателя уровня бензина. Фактическое количество (масса) бензина, оставшегося в баке, когда датчик показывает «пусто», летом намного меньше, чем зимой. Бензин имеет тот же объем, что и зимой, когда загорается индикатор «добавьте топливо», но из-за того, что бензин расширился, масса стала меньше. Если вы привыкли проезжать еще 40 миль «пустым» зимой, будьте осторожны — летом вы, вероятно, выбежите гораздо быстрее. 9{\circ}\textbf{C}}?[/latex] Стратегия Бак и бензин увеличиваются в объеме, но бензин увеличивается больше, поэтому количество пролитого равно разнице в изменении их объема. (Бензиновый бак можно рассматривать как твердую сталь.) Мы можем использовать уравнение для расширения объема, чтобы вычислить изменение объема бензина и бака. Решение 1. Используйте уравнение для объемного расширения, чтобы рассчитать увеличение объема стального резервуара: [латекс] \boldsymbol{\Delta{V}_{\textbf{s}}=\beta_{\textbf{s}}V_{\textbf{s}}\Delta{T}}.[/latex] 2. Увеличение объема бензина определяется следующим уравнением: \textbf{gas}}\Delta{T}}.[/latex] 3. Найдите разницу в объеме, чтобы определить количество пролитого вещества как [латекс]\boldsymbol{V _{\textbf{spill}}=\ Delta{V}_{\textbf{gas}}-\Delta{V}_{\textbf{s}}}.[/latex] В качестве альтернативы мы можем объединить эти три уравнения в одно уравнение. (Обратите внимание, что исходные объемы равны.) 9{\circ}\textbf{C})} \\ {} & \boldsymbol{=} & \boldsymbol{1.10\textbf{L.}} \end{array}[/latex] Обсуждение Это количество является значительным, особенно для бака на 60,0 л. Эффект настолько поразителен, потому что бензин и сталь быстро расширяются. Скорость изменения термических свойств обсуждается в главе 14 «Тепло и методы теплопередачи». Если вы попытаетесь плотно закрыть бак, чтобы предотвратить переполнение, вы обнаружите, что он все равно протекает, либо вокруг крышки, либо из-за разрыва бака. Плотное сжатие расширяющегося газа эквивалентно его сжатию, а как жидкости, так и твердые тела сопротивляются сжатию с чрезвычайно большими силами. Чтобы избежать разрыва жестких контейнеров, эти контейнеры имеют воздушные зазоры, которые позволяют им расширяться и сжиматься, не нагружая их. Термическое напряжение создается тепловым расширением или сжатием (см. главу 5.3 Эластичность: напряжение и деформация для обсуждения напряжения и деформации). Термическое напряжение может быть разрушительным, например, когда расширяющийся бензин разрывает бак. Это также может быть полезно, например, когда две детали соединяются вместе путем нагревания одной в процессе производства, затем надевания ее на другую и охлаждения комбинации. Термический стресс может объяснить многие явления, такие как выветривание горных пород и дорожного покрытия из-за расширения льда при замерзании. Стратегия Чтобы решить эту задачу, мы должны использовать следующее уравнение, которое связывает изменение объема[ латекс]\boldsymbol{\Delta{V}}[/latex]к давлению: [латекс]\boldsymbol{\Delta{V}\:=}[/latex][латекс]\boldsymbol{\frac{1} {B}\frac{F}{A}}[/latex][latex]\boldsymbol{V_0,}[/latex] , где[latex]\boldsymbol{F/A}[/latex] – давление,[ латекс]\boldsymbol{V_0}[/latex]– первоначальный объем, а [латекс]\boldsymbol{B}[/latex]– модуль объемного сжатия используемого материала. Мы будем использовать количество, пролитое в Примере 2, как изменение объема,[латекс]\жирныйсимвол{\Delta{V}}.[/латекс] 92},[/latex] намного больше, чем может выдержать бензобак. Силы и давления, создаваемые термическим напряжением, обычно такие же большие, как и в приведенном выше примере. Железнодорожные пути и проезжие части могут деформироваться в жаркие дни, если на них недостаточно компенсационных швов.  (кредит: Editor5807, Wikimedia Commons)Металл регулярно используется в человеческом теле для имплантатов бедра и колена. Большинство имплантатов со временем необходимо заменять, потому что, среди прочего, металл не сцепляется с костью. Исследователи пытаются найти лучшие металлические покрытия, которые позволили бы связывать металл с костью. Одна из задач состоит в том, чтобы найти покрытие с коэффициентом расширения, аналогичным коэффициенту расширения металла. Если коэффициенты расширения слишком разные, термические напряжения в процессе производства приводят к трещинам на границе раздела покрытие-металл. Еще один пример термического стресса обнаружен во рту. Зубные пломбы могут расширяться иначе, чем зубная эмаль. Это может вызывать боль при употреблении мороженого или горячего напитка. В пломбе могут появиться трещины. Металлические пломбы (золото, серебро и др.) вытесняются композитными пломбами (фарфор), имеющими меньшие коэффициенты расширения и более близкие к зубным.
Объемные температурные коэффициенты –β – для некоторых жидкостей
Преобразование между метрическими и британскими объемными температурными коэффициентами )Пример – объемное расширение масла
90 280 100 л – 0,1 м 3 – масла с коэффициент объемного расширения 0,00070 1/ o C нагревается от 20 o C до 40 o C . dV = (0,1 м 3 ) (0,00070 1/ o C) ((40 o C) – ( 20 или С )) = 0,0014 м 3 = 1,4 литра Конечный объем 90 002 100 литров + 1,4 литра = 101,4 литраПример – кубическое расширение масла30 галлонов США масла нагревается от 7 0 o F до 100 o F 90 281 . Объемное расширение можно рассчитать по уравнению (2) dV = (30 галлонов) (0,00039 1/ o F) ((100 o F) – (70 o 90 229 Ж)) = 0,351 галлона Конечный объем 30 галлонов + 0,351 галлона = 30,351 галлона , жидкости и газы. Определения и калькуляторы конвертации. Рекламные ссылки Добавляйте стандартные и настраиваемые параметрические компоненты, такие как балки с полками, пиломатериалы, трубопроводы, лестницы и т. д., в свою модель Sketchup с помощью Engineering ToolBox — расширения SketchUp, которое можно использовать с потрясающими, увлекательными и бесплатными программами SketchUp Make и SketchUp Pro. . Добавьте расширение Engineering ToolBox в свой SketchUp из хранилища расширений SketchUp Pro Sketchup! Перевести О Engineering ToolBox! Мы не собираем информацию от наших пользователей. |
|---|
[/latex] 9{\circ}\textbf{C})=0,84\textbf{ м.}}[/latex]
[/latex]Обратите внимание, что значения [латекс]\boldsymbol {\beta}[/latex]в таблице 2 почти точно равны[latex]\boldsymbol{3\alpha}.[/latex] 9{\circ}\textbf{C}}[/latex] вода подо льдом из-за этой необычной характеристики воды. Он также производит циркуляцию воды в пруду, что необходимо для здоровой экосистемы водоема.
Бензин охлаждает стальной бак, когда он заполнен. И бензин, и стальной бак расширяются при нагревании до температуры воздуха, но бензин расширяется гораздо больше, чем сталь, поэтому он может перелиться через край.
92}.[/latex](Дополнительные сведения о объемном модуле см. в главе 5.3 Эластичность: напряжение и деформация.)
(См. рис. 5.) Линии электропередач провисают больше летом, чем зимой, и ломаются в холодную погоду, если провисание недостаточное. Трещины в оштукатуренных стенах открываются и закрываются по мере того, как дом нагревается и остывает. Стеклянные кастрюли треснут при быстром или неравномерном охлаждении из-за дифференциального сжатия и создаваемых им напряжений. (Pyrex® менее чувствителен из-за его низкого коэффициента теплового расширения.) Корпусам высокого давления ядерных реакторов угрожает чрезмерно быстрое охлаждение, и, хотя ни один из них не вышел из строя, некоторые охлаждались быстрее, чем считалось желательным. Биологические клетки разрушаются при замораживании продуктов, что ухудшает их вкус. Многократное оттаивание и замораживание усугубляют ущерб. Даже океаны могут быть затронуты. Значительная часть повышения уровня моря в результате глобального потепления связана с тепловым расширением морской воды. 
[/латекс]Термическое напряжение создается, когда тепловое расширение ограничено. 9{\circ}\textbf{C}}[/latex]изменение температуры
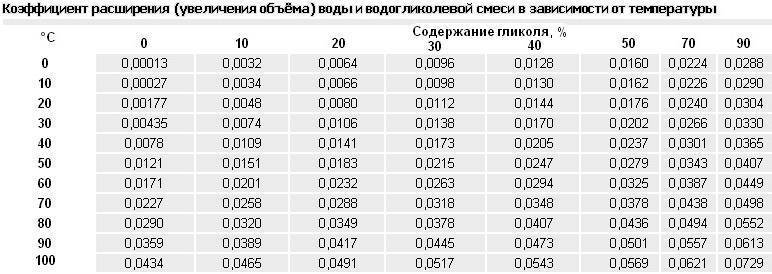
Приведенный ниже калькулятор является универсальным и может использоваться для метрических и имперских единиц при условии, что единицы используются последовательно.
Пример – вода – это жидкость, коэффициент объемного расширения которой сильно меняется в зависимости от температуры. Вода имеет наибольшую плотность и наименьший объем при 4 или C (39.2 или F) . Объемный коэффициент для воды отрицателен ниже 4 o C и показывает, что объем a уменьшается при изменении температуры от 0 o C ( 32 o F ) до 4 o C .
Объемное расширение можно рассчитать по уравнению (2) 
д.
