Вода как теплоноситель — ТеплоВики
Материал из ТеплоВики – энциклопедия отоплении
Наиболее важными свойствами воды являются:
Физические свойства воды
Удельная теплоемкость
Важным свойством любого теплоносителя является его теплоёмкость. Если выразить ее через массу и разность температур теплоносителя, то получится удельная теплоёмкость.
Она обозначается буквой c и имеет размерность кДж/(кг • K)
Удельная теплоемкость — это количество тепла, которое необходимо передать 1 кг вещества (например, воды), чтобы нагреть его на 1 °C. И наоборот, вещество отдает такое же количество энергии при охлаждении.
Среднее значение удельной теплоемкости воды в диапазоне между 0 °C и 100 °C составляет:
c = 4,19 кДж/(кг • K) или c = 1,16 Втч/(кг • K)
Количество поглощаемого или выделяемого тепла Q, выраженное в Дж или кДж, зависит от массы m, выраженной в кг, удельной теплоемкости c и разности температур, выраженной в K.
В системах отопления — это разность температур в прямом и обратном трубопроводе. Полученная формула:
Q = m • c • Δϑ
m= V • ρ
V = Объем воды в м3
ρ = Плотность в кг/м3
Масса m — это объем воды V, выраженный в м3, умноженный на плотность ρ воды, выраженную в кг/м3. Таким образом, формулу можно представить в следующем виде:
Q = V • ρ • c ( ϑV – ϑR)
Известно, что плотность воды меняется в зависимости от ее температуры. Однако, чтобы упростить расчеты, используется = 1 кг/дм3 в диапазоне от 4 °C до 90 °C.
Физические термины “энергия”, “работа” и “количество тепла” эквивалентны.
Следующая формула используется для преобразования джоулей в другие размерности:
1 Дж = 1 Нм = 1 Втс или 1 МДж = 0,278 кВтч
Увеличение и уменьшение объема
Изменение объема воды Когда вода нагревается или охлаждается, ее плотность уменьшается.Все природные материалы расширяются при нагревании и сжимаются при охлаждении. Единственным исключением из этого правила является вода. Это уникальное ее свойство называется аномалией воды.
Вода имеет наибольшую плотность при +4 °C, при которой 1 дм3 = 1 л имеет массу 1 кг. Если вода нагревается или охлаждается относительно этой точки, ее объем увеличивается, что означает уменьшение плотности, т. е. вода становится легче.
Это можно отчетливо наблюдать на примере резервуара с точкой перелива.
В резервуаре находится ровно 1000 см3 воды с температурой +4 °C. При нагревании воды некоторое количество выльется из резервуара в мерную емкость. Если нагреть воду до 90 °C, в мерную емкость выльется ровно 35,95 см3, что соответствует 34,7 г.
Характеристики кипения воды
Изменение агрегатного состояния при повышении температурыЕсли воду нагревать в открытой емкости, она закипит при температуре 100 °C. Если измерять температуру кипящей воды, окажется, что она остается равной 100 °C пока не испарится последняя капля. Таким образом, постоянное потребление тепла используется для полного испарения воды, т. е. изменения ее агрегатного состояния. Эта энергия также называется латентной (скрытой) теплотой. Если подача тепла продолжается, температура образовавшегося пара снова начнет подниматься.
Описанный процесс приведен при давлении воздуха 101,3 кПа у поверхности воды. При любом другом давлении воздуха точка кипения воды сдвигается от 100 °C.
Если бы мы повторили описанный эксперимент на высоте 3000 м. — мы бы обнаружили, что вода там закипает уже при 90 °C. Причиной такого поведения является понижение атмосферного давления с высотой.
Чем ниже давление на поверхности воды, тем ниже будет температура кипения. И наоборот, температура кипения будет выше при повышении давления на поверхности воды. Это свойство используется, например, в скороварках.
График справа показывает зависимость температуры кипения воды от давления.
Расширение воды при нагревании и защита от избыточного давления
Системы водяного отопления работают при температурах воды до 90 °C. Обычно система заполняется водой при температуре 15 °C, которая затем расширяется при нагревании. Нельзя допустить, чтобы это увеличение объема привело к возникновению избыточного давления и переливу жидкости.
Система отопления со встроенным предохранительным клапаномКогда отопление отключается в летний период, объем воды возвращается к первоначальному значению. Таким образом, для обеспечения беспрепятственного расширения воды необходимо установить достаточно большой бак. Старые системы отопления имели открытые расширительные баки. Они всегда располагались выше самого высокого участка трубопровода. При повышении температуры в системе, что приводило к расширению воды, уровень в баке также повышался. При снижении температуры он, соответственно, понижался.
Современные системы отопления используют мембранные расширительные баки (МРБ).
При повышении давления в системе нельзя допускать увеличения давления в трубопроводах и других элементах системы выше предельного значения. Поэтому обязательным условием для каждой системы отопления является наличие предохранительного клапана.
При повышении давления сверх нормы предохранительный клапан должен открываться и стравливать лишний объем воды, который не может вместить расширительный бак. Тем не менее, в тщательно спроектированной и обслуживаемой системе такое критическое состояние никогда не должно возникать.
Все эти рассуждения не учитывают тот факт, что циркуляционный насос еще больше увеличивает давление в системе.
Взаимосвязь между максимальной температурой воды, выбранным насосом, размером расширительного бака и давлением срабатывания предохранительного клапана должна быть установлена самым тщательным образом. Случайный выбор элементов системы — даже на основании их стоимости — в данном случае неприемлем.
Мембранный расширительный бак поставляется заполненным азотом. Начальное давление в расширительном мембранном баке должно быть отрегулировано в зависимости от системы отопления. Расширяющаяся вода из системы отопления поступает в бак и сжимает газовую камеру через диафрагму. Газы могут сжиматься, а жидкости — нет.
Компенсация изменения объема воды в системе отопления:
До заполнения системы водой Система заполнена холодной водой Система при макс. температуре водыДавление
Определение давления
Давление — это статическое давление жидкостей и газов, измеренное в сосудах, трубопроводах относительно атмосферного
давления (Па, мбар, бар).
Статическое давление
Статическое давление — это давление неподвижной жидкости.
Статическое давление = уровень выше соответствующей точки измерения + начальное давление в расширительном баке.
Динамическое давление
Динамическое давление — это давление движущегося потока жидкости.
Давление нагнетания насоса
Это давление на выходе центробежного насоса во время его работы.
Перепад давления
Давление, развиваемое центробежным насосом для преодоления общего сопротивления системы. Оно измеряется между входом и выходом центробежного насоса.
Рабочее давление
Давление, имеющееся в системе при работе насоса.
Допустимое рабочее давление
Максимальное значение рабочего давления, допускаемого из условий безопасности работы насоса и системы.
Кавитация
Кавитация — это образование пузырьков газа в результате появления локального давления ниже давления парообразования перекачиваемой жидкости на входе рабочего колеса. Это приводит к снижению производительности (напора) и КПД и вызывает шумы и разрушение материала внутренних деталей насоса.
Из-за схлопывания пузырьков воздуха в областях с более высоким давлением (например, на выходе рабочего колеса) микроскопические взрывы вызывают скачки давления, которые могут повредить или разрушить гидравлическую систему. Первым признаком этого служит шум в рабочем колесе и его эрозия.
Важным параметром центробежного насоса является NPSH (высота столба жидкости над всасывающим патрубком насоса). Он определяет минимальное давление на входе насоса, требуемое данным типом насоса для работы без кавитации, т. е. дополнительное давление, необходимое для предотвращения появления пузырьков.
На значение NPSH влияют тип рабочего колеса и частота вращения насоса. Внешними факторами, влияющими на данный параметр, являются температура жидкости, атмосферное давление.
Предотвращение кавитации
Чтобы избежать кавитации, жидкость должна поступать на вход центробежного насоса при определенной минимальной высоте всасывания, которая зависит от температуры и атмосферного давления.
Другими способами предотвращения кавитации являются:
- Повышение статического давления
- Понижение температуры жидкости (снижение давления парообразования PD)
- Выбор насоса с меньшим значением постоянного гидростатического напора (минимальная высота всасывания, NPSH)
ru.teplowiki.org
Расчет полезного объема расширительного бака | Расширительный бак
Страница 4 из 4
Расчет полезного объема расширительного бака
Номинальный объем открытого расширительного бака (Vhom) соответствует увеличению объема воды в системе отопления при ее нагревании до средней расчетной температуры (DVc).
Увеличение объема воды в системе при нагревании (DVc) вычисляют по формулам:
DVc = к х Vc, л или DVc = b х Dt х Vc, л где Vc – общий объем воды в системе отопления при начальной температуре (соответствует общему внутреннему объему труб с арматурой, отопительных приборов, водогрейного котла и пр.), л
Dt – изменение температуры воды от начальной до средней расчетной, “С
к – коэффициент объемного расширения воды (см. таблицу)
b – среднее значение коэффициента объемного расширения воды (составляет 0,0006)
Общий объем воды в системе отопления при начальной температуре вычисляют по формуле: Vc = Vnp х Qc + еУэл, л
где Vnp – объем воды в системе отопления в зависимости от объема воды в основных элементах системы (см. таблицу), л/кВт
Qc – тепловая мощность система, кВт eVaл – суммарный объем воды в дополнительных элементах (котлах, теплообменниках, калориферах, воздухосборниках и пр.), л
Таким образом, полезный объем открытого расширительного бака равен:
Vhom = k х Vc или Vhom = b х Dt х Vc Номинальный объем закрытого расширительного бака с переменным давлением
VHa4 – начальный запас воды в закрытом расширительном баке,л
рк – конечное значение избыточного давления в расширительном баке при максимальной температуре воды в системе, МПа
ро – избыточное давление в газовой камере расширительного бака до первого поступления в него воды, Мпа Начальный запас воды в закрытом расширительном баке (\/нач) должен составлять порядка 20 % от номинального объема демпфера (Vhom), если 3 л < Vhom < 15 л, и 0,5 % от общего объема воды в системе отопления (Vc), если Vhom > 15 л.
‘ Чтобы обеспечить начальный запас воды в баке (VHa4), необходимо при заполнении системы отопления водой создать начальное избыточное давление в системе (рнач) на уровне установки бака. Начальное избыточное давле- ние(рнач) определяют по формуле:
рнач = (Vn (ро + 0,1) / Vn – Унач) – 0,1, МПа Полезный объем закрытого расширительного бака с постоянным избыточным давлением и установки с управляющим насосом (Упол) всегда составляет 80 % от полного объема и вычисляют по формуле: Упол = (DVc + Унач) / 0,8, л
Тип установки с управляющим насосом подбирают в зависимости от гидростатического давления в системе и в соответствии с его техническими характеристиками. Номинальное значение расхода управляющего насоса (Ghom) определяют по формуле: Ghom = 0,85 Qc, л/ч
Следует иметь в виду, что при недостаточном объеме закрытого расширительного бака вероятность повышения водяного давления в отопительной системе многократно возрастает, что может привести к взрыву трубопровода.
Таблица. Объемное расширение нагреваемой воды
| Расчетная температура воды, *С | Объемное расширение воды, в долях первоначального объема |
| 85 | 0,022 |
| 95 | 0,024 |
| 105 | 0,027 |
| 110 | 0,029 |
| 115 | 0,031 |
| 130 | 0,035 |
| 135-150 | 0,042 |
Таблица. Объем воды в системе отопления
| Вид отопительных приборов | Объем воды при расчетной температуре горячей воды, равной 95’С, л/вКт |
| Конвекторы | 4,6 |
| Воздушные отопительные | 6,2 |
| приборы | |
| Панельные радиаторы | 8,5 |
| Секционные радиаторы | 10,8 |
| Секционные радиаторы боль | 15,5 |
| шой протяженности | |
| Гладкие трубы | 31,6 |
Таблица. Поправочные коэффициенты объемного расширения вод
| Температура воды в подающей линии, •с | Коэффициент объемного расширения воды |
| 50 | 3,37 |
| 55 | 2,78 |
| 60 | 2,37 |
| 65 | 2,02 |
| 70 | 1,77 |
| 75 | 1,54 |
| 80 | 1.37 |
| 85 | 1,22 |
| 90 | 1.11 |
| 100 | 0,91 |
| 105 | 0.83 |
| 110 | 0.77 |
| 115 | 0,71 |
| 120 | 0,66 |
domsnulya.ru
Коэффициент температурного расширения
Определение и формула коэффициента температурного расширения
При изменении температуры происходит изменение размеров твердого тела, которое называют тепловым расширением. Различают линейное и объемное тепловое расширения. Эти процессы характеризуют коэффициентами теплового (температурного) расширения: — средний коэффициент линейного температурного расширения, средний коэффициент объемного теплового расширения.
Применяют, обычно средний коэффициент линейного расширения. Это характеристика теплового расширения материала.
Если первоначальная длина тела равна , — его удлинение при увеличении температуры тела на , тогда определен формулой:
Коэффициент линейного удлинения является характеристикой относительного удлинения (), которое происходит при увеличении температуры тела на 1К.
При увеличении температуры увеличивается объем твердого тела. В первом приближении можно считать, что:
где — начальный объем тела, — изменение температуры тела. Тогда коэффициентом объемного расширения тела является физическая величина, которая характеризует относительное изменение объема тела (), которое происходит при нагревании тела на 1 K и неизменном давлении. Математическим определением коэффициента объемного расширения является формула:
Тепловое расширение твердого тела связывают с ангармоничностью тепловых колебаний частиц, составляющих кристаллическую решетку тела. В результате данных колебаний при увеличении температуры тела увеличивается равновесное расстояние между соседними частицами этого тела.
При изменении объема тела происходит изменение его плотности:
где — начальная плотность, — плотность вещества при новой температуре. Так как величина то выражение (4) иногда записывают как:
Коэффициенты теплового расширения зависят от вещества. В общем случае они будут зависеть от температуры. Коэффициенты теплового расширения считают независимыми от температуры в небольшом интервале температур.
Существует ряд веществ, имеющих отрицательный коэффициент теплового расширения. Так при повышении температуры такие материалы сжимаются. Обычно это происходит в узком интервале температур. Есть вещества, у которых коэффициент теплового расширения почти равен нулю около некоторого определенного интервала температур.
Выражение (3) применяют не только для твердых тел, но и жидкостей. При этом считают, что коэффициент температурного расширения для капельных жидкостей изменяется при изменении температуры не существенно. Однако при расчете систем отопления его учитывают.
Связь коэффициентов теплового расширения
В первом приближении можно считать, что коэффициенты линейного и объемного расширения изотропного тела связаны соотношением:
Единицы измерения
Основной единицей измерения коэффициентов температурного расширения в системе СИ является:
Примеры решения задач
ru.solverbook.com
Предложена новая теория, объясняющая, почему вода при нагревании от 0 до 4°C сжимается
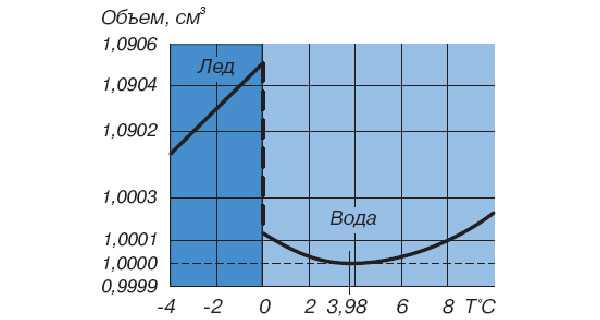
Японский физик Масакадзу Мацумото выдвинул теорию, которая объясняет, почему вода при нагревании от 0 до 4°C сжимается, вместо того чтобы расширяться. Согласно его модели, вода содержит микрообразования — «витриты», представляющие собой выпуклые пустотелые многогранники, в вершинах которых находятся молекулы воды, а ребрами служат водородные связи. При повышении температуры конкурируют между собой два явления: удлинение водородных связей между молекулами воды и деформация витритов, приводящая к уменьшению их полостей. В диапазоне температур от 0 до 3,98°C последнее явление доминирует над эффектом удлинения водородных связей, что в итоге и дает наблюдаемое сжатие воды. Экспериментального подтверждения модели Мацумото пока что нет — впрочем, как и других теорий, объясняющих сжатие воды.
В отличие от подавляющего большинства веществ, вода при нагревании способна уменьшать свой объем (рис. 1), то есть обладает отрицательным коэффициентом теплового расширения. Впрочем, речь идет не обо всём температурном интервале, где вода существует в жидком состоянии, а лишь об узком участке — от 0°C примерно до 4°C. При больших температурах вода, как и другие вещества, расширяется.
Между прочим, вода — не единственное вещество, имеющее свойство сжиматься при увеличении температуры (или расширяться при охлаждении). Подобным поведением могут «похвастать» еще висмут, галлий, кремний и сурьма. Тем не менее, в силу своей более сложной внутренней структуры, а также распространенности и важности в разнообразных процессах, именно вода приковывает внимание ученых (см. Продолжается изучение структуры воды, «Элементы», 09.10.2006).
Некоторое время назад общепринятой теорией, отвечающей на вопрос, почему вода увеличивает свой объем при понижении температуры (рис. 1), была модель смеси двух компонент — «нормальной» и «льдоподобной». Впервые эта теория была предложена в XIX веке Гарольдом Витингом и позднее была развита и усовершенствована многими учеными. Сравнительно недавно в рамках обнаруженного полиморфизма воды теория Витинга была переосмыслена. Отныне считается, что в переохлажденной воде существует два типа льдообразных нанодоменов: области, похожие на аморфный лед высокой и низкой плотности. Нагревание переохлажденной воды приводит к плавлению этих наноструктур и к появлению двух видов воды: с большей и меньшей плотностью. Хитрая температурная конкуренция между двумя «сортами» образовавшейся воды и порождает немонотонную зависимость плотности от температуры. Однако пока эта теория не подтверждена экспериментально.
С приведенным объяснением нужно быть осторожным. Не случайно здесь говорится лишь о структурах, которые напоминают аморфный лед. Дело в том, что наноскопические области аморфного льда и его макроскопические аналоги обладают разными физическими параметрами.
Японский физик Масакадзу Мацумото решил найти объяснение обсуждаемого здесь эффекта «с нуля», отбросив теорию двухкомпонентной смеси. Используя компьютерное моделирование, он рассмотрел физические свойства воды в широком диапазоне температур — от 200 до 360 К при нулевом давлении, чтобы в молекулярном масштабе выяснить истинные причины расширения воды при ее охлаждении. Его статья в журнале Physical Review Letters так и называется: Why Does Water Expand When It Cools? («Почему вода при охлаждении расширяется?»).
Изначально автор статьи задался вопросом: что влияет на коэффициент теплового расширения воды? Мацумото считает, что для этого достаточно выяснить влияние всего трех факторов: 1) изменения длины водородных связей между молекулами воды, 2) топологического индекса — числа связей на одну молекулу воды и 3) отклонения величины угла между связями от равновесного значения (углового искажения).
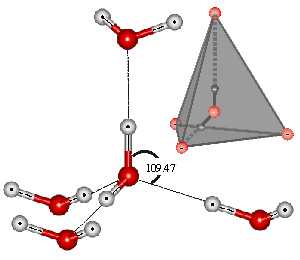
Перед тем как рассказать о результатах, полученных японским физиком, сделаем важные замечания и разъяснения по поводу вышеупомянутых трех факторов. Прежде всего, привычная химическая формула воды H2O соответствует лишь парообразному ее состоянию. В жидкой форме молекулы воды посредством водородной связи объединяются в группы (H2O)x, где x — количество молекул. Наиболее энергетически выгодно объединение из пяти молекул воды (x = 5) с четырьмя водородными связями, в котором связи образуют равновесный, так называемый тетраэдральный угол, равный 109,47 градуса (см. рис. 2).
Проанализировав зависимость длины водородной связи между молекулами воды от температуры, Мацумото пришел к ожидаемому выводу: рост температуры рождает линейное удлинение водородных связей. А это, в свою очередь, приводит к увеличению объема воды, то есть к ее расширению. Сей факт противоречит наблюдаемым результатам, поэтому далее он рассмотрел влияние второго фактора. Как коэффициент теплового расширения зависит от топологического индекса?
Компьютерное моделирование дало следующий результат. При низких температурах наибольший объем воды в процентном отношении занимают кластеры воды, у которых на одну молекулу приходится 4 водородных связи (топологический индекс равен 4). Повышение температуры вызывает уменьшение количества ассоциатов с индексом 4, но при этом начинает возрастать число кластеров с индексами 3 и 5. Проведя численные расчеты, Мацумото обнаружил, что локальный объем кластеров с топологическим индексом 4 с повышением температуры практически не меняется, а изменение суммарного объема ассоциатов с индексами 3 и 5 при любой температуре взаимно компенсирует друг друга. Следовательно, изменение температуры не меняет общий объем воды, а значит, и топологический индекс никакого воздействия на сжатие воды при ее нагревании не оказывает.
Остается выяснить влияние углового искажения водородных связей. И вот здесь начинается самое интересное и важное. Как было сказано выше, молекулы воды стремятся объединиться так, чтобы угол между водородными связями был тетраэдральным. Однако тепловые колебания молекул воды и взаимодействия с другими молекулами, не входящими в кластер, не дают им этого сделать, отклоняя величину угла водородной связи от равновесного значения 109,47 градуса. Чтобы как-то количественно охарактеризовать этот процесс угловой деформации, Мацумото с коллегами, основываясь на своей предыдущей работе Topological building blocks of hydrogen bond network in water, опубликованной в 2007 году в Journal of Chemical Physics, выдвинули гипотезу о существовании в воде трехмерных микроструктур, напоминающих выпуклые полые многогранники. Позднее, в следующих публикациях, такие микроструктуры они назвали витритами (рис. 3). В них вершинами являются молекулы воды, роль ребер играют водородные связи, а угол между водородными связями — это угол между ребрами в витрите.
Согласно теории Мацумото, существует огромное разнообразие форм витритов, которые, как мозаичные элементы, составляют большую часть структуры воды и которые при этом равномерно заполняют весь ее объем.
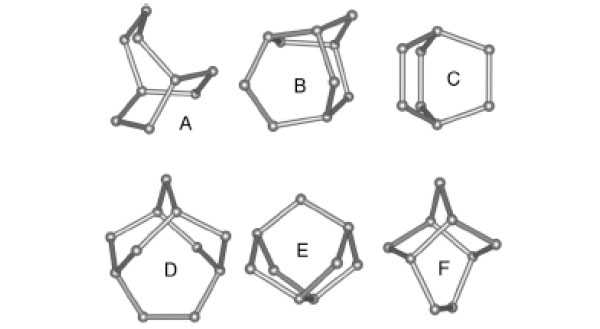
Молекулы воды стремятся создать в витритах тетраэдральные углы, поскольку витриты должны обладать минимально возможной энергией. Однако из-за тепловых движений и локальных взаимодействий с другими витритами некоторые микроструктуры не обладают геометрией с тетраэдральными углами (или углами, близкими к этому значению). Они принимают такие структурно неравновесные конфигурации (не являющиеся для них самыми выгодными с энергетической точки зрения), которые позволяют всему «семейству» витритов в целом получить наименьшее значение энергии среди возможных. Такие витриты, то есть витриты, которые как бы приносят себя в жертву «общим энергетическим интересам», называются фрустрированными. Если у нефрустрированных витритов объем полости максимален при данной температуре, то фрустрированные витриты, напротив, обладают минимально возможным объемом.
Компьютерное моделирование, проведенное Мацумото, показало, что средний объем полостей витритов с ростом температуры линейным образом уменьшается. При этом фрустрированные витриты значительно уменьшают свой объем, тогда как объем полости нефрустрированных витритов почти не меняется.
Итак, сжатие воды при увеличении температуры вызвано двумя конкурирующими эффектами — удлинением водородных связей, которое приводит к увеличению объема воды, и уменьшением объема полостей фрустрированных витритов. На температурном отрезке от от 0 до 4°C последнее явление, как показали расчеты, преобладает, что в итоге и приводит к наблюдаемому сжатию воды при повышении температуры.
Осталось дождаться экспериментального подтверждения существования витритов и такого их поведения. Но это, увы, очень непростая задача.
Источник: Masakazu Matsumoto. Why Does Water Expand When It Cools? // Phys. Rev. Lett. 103, 017801 (2009).
Юрий Ерин
elementy.ru
Особенности расширения воды
Самое распространенное на поверхности Земли вещество — вода — имеет особенность, отличающую ее от большинства других жидкостей. Она расширяется при нагревании только свыше , от 0 до объем воды, наоборот, при нагревании уменьшается. Таким образом, наибольшую плотность вода имеет при . Эти данные относятся к пресной (химически чистой) воде. У морской воды наибольшая плотность наблюдается примерно при . Увеличение давления тоже понижает температуру наибольшей плотности воды.
Особенности расширения воды имеют громадное значение для климата Земли. Большая часть (79%) поверхности Земли покрыта водой. Солнечные лучи, падая на поверхность воды, частично отражаются от нее, частично проникают внутрь воды и нагревают ее. Если температура воды низка, то нагревшиеся слои (например, при ) более плотны, чем холодные (например, при ), и потому опускаются вниз. Их место занимают холодные, слои, в свою очередь нагревающиеся. Таким образом, происходит непрерывная смена слоев воды, что способствует равномерному прогреванию всей толщи воды, пока не будет достигнута температура, соответствующая максимальной плотности. При дальнейшем нагревании верхние слои становятся все менее плотными, а потому и остаются вверху.
Вследствие этого большие толщи воды сравнительно легко прогреваются солнечными лучами лишь до температуры наибольшей плотности воды; дальнейшее прогревание нижних слоев идет крайне медленно. Наоборот, охлаждение воды до температуры наибольшей плотности идет сравнительно быстро, а затем процесс охлаждения замедляется. Все это ведет к тому, что глубокие водоемы на поверхности Земли имеют, начиная с некоторой глубины, температуру, близкую к температуре наибольшей плотности воды ( ). Верхние слои морей в теплых странах могут иметь температуру, значительно более высокую ( и более).
sfiz.ru
Особенности теплового расширения воды Тепловое расширение воды
У большинства веществ объем при плавлении увеличивается, а при отвердевании уменьшается, при этом изменяется и плотность вещества.
Плотность вещества при плавлении уменьшается, а при отвердевании увеличивается. Но существуют такие вещества, как, например, кремний, германий, висмут, у которых плотность при плавлении увеличивается, а при отвердевании уменьшается. К этим веществам относится и лед (вода).
Опыт показывает, что вода имеет, наибольшую плотность при 4°С. Это объясняется особенностями строения кристаллической решетки льда. Если в жидком состоянии молекулы Н2О расположены вплотную друг к другу, то при кристаллизации расстояние между ближайшими молекулами увеличивается и в кристалле между молекулами образуются «пустоты». Поэтому плотность воды больше, чем льда, и достигает наибольшего значения при 4″С. При повышении или понижении температуры от 4°С плотность воды уменьшается, объем увеличивается.
Вследствие того, что почти 80% поверхности Земли покрыто водой, особенности ее теплового расширения оказывают огромное влияние на климат Земли. При нагревании воды в открытых водоемах, имеющей температуру 1—2°С, происходит непрерывная смена слоев воды, имеющих различную температуру. Так происходит до тех пор* пока не будет достигнута температура, соответствующая максимальной плотности. При дальнейшем нагревании верхние слои становятся менее плотными, а потому остаются наверху. Этим объясняется тот факт, что в глубоких водоемах температура воды, начиная с некоторой глубины близка к температуре наибольшей плотности воды.
Этой особенностью теплового расширения воды объясняется тот факт, что водоемы зимой не промерзают до дна. При охлаждении, пока температура поверхностного слоя не достигнет 4°С, плотность более теплой воды ниже плотности более холодной, поэтому более теплая вода поднимается вверх, а более холодная опускается вниз.
В интервале температур от 0 до 4°С значения плотностей меняются: теперь уже вода, имеющая более высокую температуру, опускается вниз, г более холодная перемещается вверх и, охлаждаясь, замерзает.
Расширение воды при замерзании ведет к разрушению горных пород, сосудов, в которых она находится.
2. Фотоэффект.
В 1900 г. немецкий физик Макс Планк высказал гипотезу: свет излучается и поглощается отдельными порциями — квантами (или фотонами). Энергия каждого фотона определяется формулой Е = hv, где h — постоянная Планка, равная 6,63 • 10 Дж • с, v — частота света. Гипотеза Планка объяснила многие явления: в частности, явление фотоэффекта, открытого в 1887 г. немецким ученым Генрихом Герцем и изученного экспириментально русским ученым Александром Григорьевичем Столетовым.
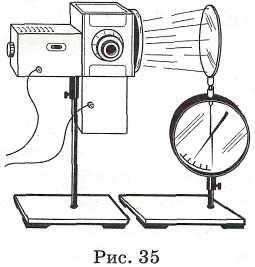
Фотоэффект — это явление испускания электронов веществом под действием света. Если зарядить цинковую пластину, присоединенную к электрометру, отрицательно и освещать ее электрической дугой (рис. 35), то электрометр быстро разрядится.
В результате исследований были установлены следующие эмпирические закономерности:
— количество электронов, вырываемых светом с поверхности металла за 1 с, прямо пропорционально поглощаемой за это время энергии световой волны;
— максимальная кинетическая энергия фотоэлектронов линейно возрастает с частотой света и не зависит от его интенсивности.
Кроме того, были установлены два фундаментальных свойства.
Во-первых, безынерционность фотоэффекта: процесс начинается сразу в момент начала освещения.
Во-вторых, наличие характерной для каждого металла минимальной частоты vmin — красной границы фотоэффекта. Эта частота такова, что при v < vmin фотоэффект не происходит при любой энергии света, а если v > vmin, то фотоэффект начинается даже при малой энергии.
Теорию фотоэффекта создал немецкий ученый А. Эйнштейн в 1905 г.
В основе теории Эйнштейна лежит понятие работы выхода электронов из металла и понятие о квантовом излучении света. По теории Эйнштейна фотоэффект имеет следующее объяснение: поглощая квант света, электрон приобретает энергию hv. При вылете из металла энергия каждого электрона уменьшается на определенную величину, которую называют работой выхода (Авых). Работа выхода — это работа, которую необходимо затратить, чтобы удалить электрон из металла.
Поэтому максимальная кинетическая энергия электронов после вылета (если нет других потерь) равна: тv /2 — hv – Авых. Следовательно, . Это уравнение носит название уравнения Эйнштейна.
Если hv < Авых, то фотоэффекта не происходит. Значит, красная граница фотоэффекта равна vmin = A/h.
Приборы, в основе принципа действия которых лежит явление фотоэффекта, называют фотоэлементами. Простейшим таким прибором является вакуумный фотоэлемент. Недостатками такого фотоэлемента являются слабый ток, малая чувствительность к длинноволновому излучению, сложность в изготовлении, невозможность использования в цепях переменного тока. Применяется в фотометрии для измерения силы света, яркости, освещенности, в кино для воспроизведения звука, в фототелеграфах и фототелефонах, в управлении производственными процессами.
Существуют полупроводниковые фотоэлементы, в которых под действием света происходит изменение концентрации носителей тока. Они используются при автоматическом управлении электрическими цепями (например, в турникетах метро), в цепях переменного тока, в качестве невозобновляемых источников тока в часах, микрокалькуляторах, проходят испытания первые солнечные автомобили, используются в солнечных батареях на искусственных спутниках Земли, межпланетных и орбитальных автоматических станциях.
С явлением фотоэффекта связаны фотохимические процессы, протекающие под действием света в фотографических материалах.
studfiles.net
Примеры гидравлических расчетов
Пример 1.1. В отопительной системе (котел, радиаторы, трубопроводы) частного дома содержится V = 0,3 м3 воды. Сколько воды дополнительно войдет в расширительный бак при нагревании от 20 до 80°С.
Решение:
Плотность воды при температуре t1 = 20°С до t2 = 80°С определим по таблице 4.1 (приложение 4):
Масса воды при начальной температуре
Объем, занимаемый водой при t2 = 80°С
Таким образом, дополнительный объем составляет
.
Пример 1.2. В отопительный котел поступает 50 м3воды при температуре t1 = 70°С. Какой объем V воды будет выходить из котла при нагреве воды до t2 = 90°С.
Решение:
Из формулы
получаем дополнительный объем воды при нагревании
Коэффициент температурного расширения находим по таблице 4.4 (Приложение 4): .
Следовательно,
Таким образом, из котла при нагревании будет выходить объем воды
Пример 1.3. Определить среднюю толщину δ известковых отложений в герметичном водоводе внутренним диаметром d = 0,3 м и длиной l = 2 км. При выпуске воды в количестве ΔV=0,05 м3 давление в водоводе падает на величину Δp = 106 Па. Считать, что отложения по диаметру и длине водовода распределены равномерно.
Решение:
Из формулы βp = , определим объем воды в водоводе с отложениями:
Коэффициент объемного сжатия воды находим по табл.4.2 (Приложение 4) 5·10-10 1/Па
Тогда
С другой стороны объем водовода с отложениями
Откуда выразим внутренний диаметр водовода с отложениями
Средняя толщина отложений
Задачи
Задача 1.1. Определить плотность жидкости ρ, полученной смешиванием объема жидкости V1 = 0,02 м3 плотностью ρ1 = 910 кг/м3 и объема жидкости V2 = 0,03 м3 плотностью ρ2 = 850 кг/м3.
Задача 1.2. Определить плотность топливной смеси (по весу) при следующем составе: керосин (ρк = 775 кг/м3) – 40%, мазут (ρм = 870 кг/м3) – 60%.
Задача 1.3. При гидравлическом испытании трубопровода длиной L = 1000 м и диаметром d = 100 мм давление поднималось от p1 = 1 МПа до p2 = 1,5 МПа. Определить объем жидкости ΔV, который был дополнительно закачан в водопровод. Коэффициент объемного сжатия βP = 4,75·10-10 1/Па.
Задача 1.4. При гидравлическом испытании трубопровода диаметром d = 0,4 м длиной L = 20 м и давление воды сначала было p1 = 5,5 МПа. Через час давление упало до p2 = 5,0 МПа. Определить, пренебрегая деформацией трубопровода, сколько воды вытекло при этом через неплотности. Коэффициент объемного сжатия βP = 4,75·10-10 1/Па.
Задача 1.5. Как изменится объем воды в системе отопления, имеющей вместимость V = 100 м3, после подогрева воды от начальной температуры t1 = 15 °C до t2 = 95 °C. Коэффициент температурного расширения βt= 0,00072 1/°С.
Задача 1.6. Трубопровод диаметром d = 500 мм и длиной L = 1000 м наполнен водой при давлении p1 = 400 кПа, и температуре воды t1 = 5 °C. Определить, пренебрегая деформациями и расширением стенок труб, давление в трубопроводе при нагревании воды в нем до t2 = 15 °C, если коэффициент объемного сжатия βP = 5,18·10-10 1/Па, а коэффициент температурного расширения βt= 150·10-6 1/°С.
Задача 1.7. Определить повышение давления, при котором начальный объем воды уменьшится на 3%. Коэффициент объемного сжатия воды βP = 4,75·10-10 1/Па.
Задача 1.8. При гидравлических испытаниях (проверке герметичности) подземного трубопровода длиной L = 500 м, диаметром d = 0,1 м давление в нем повысилось от от p1 = 0 до p2 = 1,0 МПа. Пренебрегая деформацией стенок трубопровода, определить объем воды, которую необходимо дополнительно закачать в трубопровод. Объемный модуль упругости воды принять равным Е = 2000 МПа.
Задача В.9. В трубопровод вместимостью 50 м3 во время испытаний было дополнительно закачано 0,05 м3 воды. Определить приращение давления в трубопроводе, если объемный модуль упругости воды Е = 2·109 Па.
Задача
В.10. Винтовой
плунжерный насос для тарировки манометров
работает на масле с коэффициентом
объемного сжатия βр = 0,625·10-9 1/Па. Определить на сколько оборотов
надо повернуть маховик винта, чтобы
поднять давление внутри насоса на Δp = 0,1 МПа, если объем рабочей камеры пресса V = 628 см3,
диаметр плунжера d = 20 мм, шаг винта h = 2 мм. Стенки рабочей камеры считать
недеформируемыми.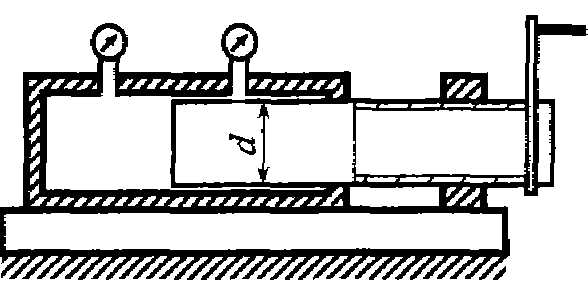
Задача 1.11. Резервуар заполнен жидкостью, объем которой V = 8 м3. Определить коэффициент температурного расширения жидкости βt, если при увеличении температуры от t1 = 10 °С до t2 = 20 °С объем жидкости увеличился на 6 л.
Задача 1.12. В отопительный котел поступает объем воды V = 80 м3 при температуре t1 = 60 °С. Какой объем воды V1 будет выходить из котла при нагреве воды до температуры t2 = 90 °С.
Задача 1.13. Для периодического аккумулирования дополнительного объема воды, получающегося при изменении температуры, к системе водяного отопления в верхней ее точке присоединяют расширительные резервуары, сообщающиеся с атмосферой. Определить наименьший объем расширительного резервуара, чтобы он полностью не опоражнивался. Допустимое колебание температуры воды во время перерывов в топке Δt = 30 °C. Объем воды в системе V = 0,7 м3. Коэффициент температурного расширения воды при средней температуре t = 80 °С βt= 6·10-4 1/°С.
Задача 1.14. Определить среднюю толщину отложений в герметичном водоводе внутренним диаметром d = 0,5 м и длиной l = 3 км. При выпуске воды объемом ΔV = 0,08 м3 давление в водоводе падает на Δр = 1 МПа. Отложения по диаметру и длине водовода распределены равномерно. Коэффициент объемного сжатия воды сжатия βр = 5·10-10 1/Па.
Задача 1.15. Стальной водовод диаметром d = 0,4 м и длиной l = 1 км, проложенный открыто, находится под давлением р = 2 МПа при температуре воды t1 = 10 °С. Определить давление воды в водоводе при повышении температуры до t2 = 15 °С в результате наружного прогрева.
Задача 1.16. Определить изменение плотности воды при увеличении давления от p1 = 100 кПа до p2 = 10000 кПа. При изменении давления температура воды не изменяется, коэффициент объемного сжатия βр = 5·10-10 1/Па.
Задача 1.17. В отопительной системе дома содержится V = 0,4 м3 воды при температуре t1 = 15°C. Определить объем воды, который дополнительно войдет в расширительный бачок при повышении температуры до t2 = 90°С.
Задача 1.18. Определить изменение плотности воды при изменении температуры от t1 = 5 °С до t2 = 95 °С.
Задача 1.19. Вязкость нефти, определенная вискозиметром, составила 4 °Е, а ее плотность ρ =880 кг/м3. Определить кинематический и динамический коэффициенты вязкости нефти.
Задача 1.20. Определить ротационным вискозиметром вязкость жидкости плотностью ρ = 920 кг/м3. Вес груза G = 80 Н, диаметры цилиндра Dц = 225 мм, барабана Dб = 223 мм, шкива d = 200 мм. Глубина погружения барабана в жидкость lб = 250 мм. Время опускания груза tгр = 12 с, путь lгр = 300 мм.
Примечание: Схема ротационного вискозиметра: в цилиндре 1 установлен барабан 2, вращающийся под действием опускающегося груза 3. Цилиндр закреплен на основании 4.
studfiles.net