Скорость движения газов в трубе
Пример. Газ поступает в газохранилище по двум трубам, диаметры которых 1 и 2- Линейная скорость движения газа в трубах одинакова и равна и. Если заменить разные трубы одинаковыми, то каков должен быть их диаметр й при условии, что общее количество поступающего газа и линейная скорость его движения должны остаться прежними [c.616]
Скорость движения газа в трубе [c.167]
Скорость движения газа в трубе определяют по расходу и сечению трубы [c.180]
Поскольку плотность продуктов сгорания уменьшается с повышением их температуры, требуется дымовая труба меньшей высоты. Тяга также улучшается с понижением температуры окружающего воздуха. Высота дымовых труб на нефтеперерабатывающих установках составляет 40—50 м и более, а создаваемое разрежение 150—200 Па. Скорость движения газов в трубе обычно принимают равной 4—8 м/с при естественной тяге и 8—16 м/с ирп искусственной, согласуя ее с величиной гидравлического сопротивления.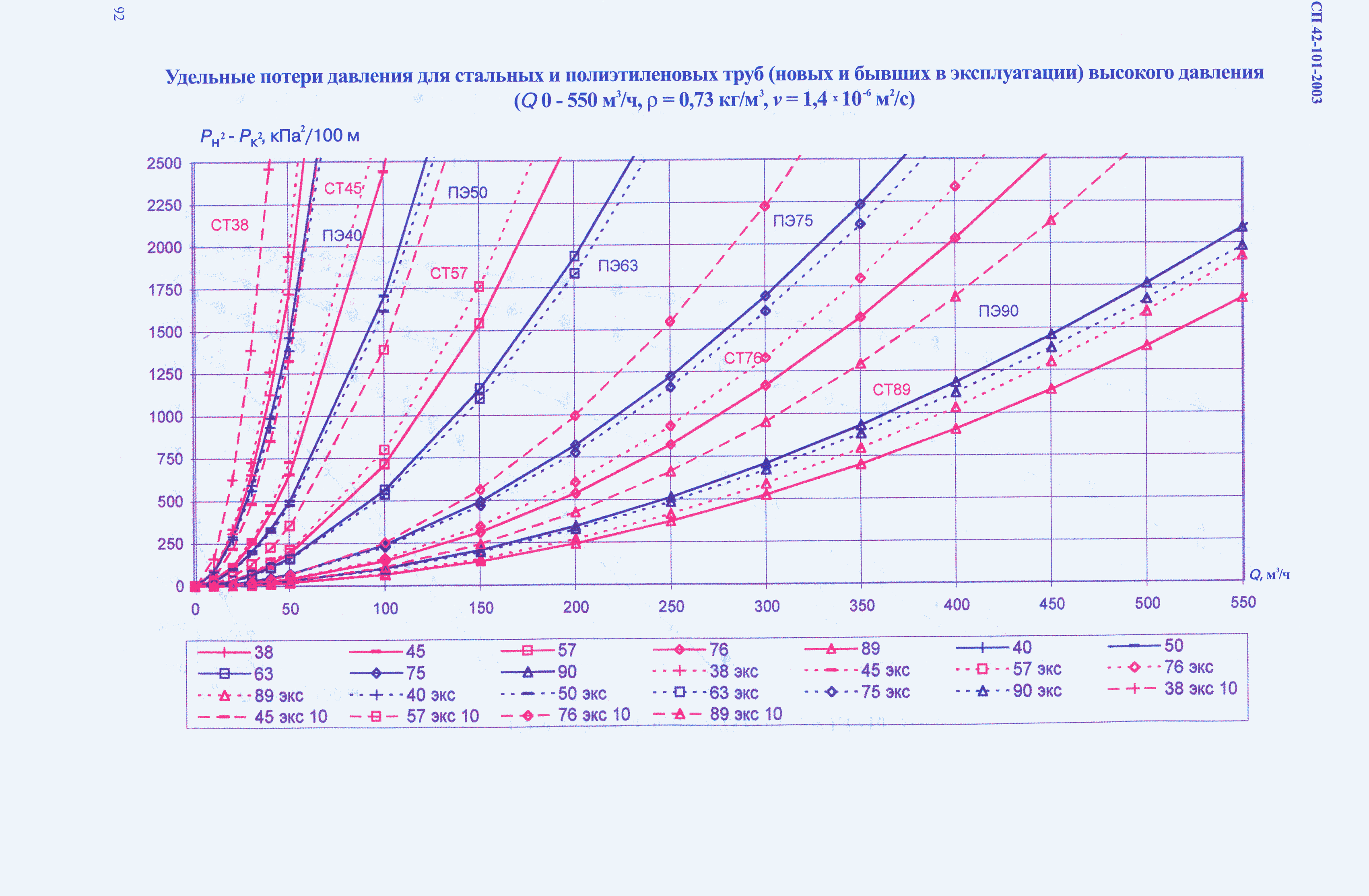
Газ по трубопроводам всегда перемещается из участков с повышенным давлением в участки, где давление ниже. Движение газа продолжается до тех пор, пока давление в системе газопроводов не выровняется. Скорость движения газа в трубе зависит от количества газа, протекающего через его поперечное сечение в единицу времени чем больше количество газа, тем больше и его скорость, чем больше диаметр трубы, тем меньшей будет скорость движения газа. [c.77]
Диапазон изменения начальной скорости движения газов в трубе—15 — 30 м/сек, концентрацпи 0,1—5 кг/кг, температуры 20 — 300 °С.
[c.84]
Пример, Газ поступает в газохранилище по двум трубам, имеющим диаметры и , линейные скорости движения газа в трубах соответственно равны г , и Если заменить обе трубы двум/1 новыми трубами одинакового диаметра, то каким должен быть этот диаметр (1. чтобы общая пропускная способность труб и линейная скорость газа в каждой трубе остались прежними [c.440]
Скорость движения газа в трубах (секциях) электрофильтра [c.43]
Для применения рассматриваемого метода к решению задачи необходимо также выяснить вопрос о сжимаемости исследуемой среды. В тех случаях, когда скорость движения газа в трубе мала по сравнению со скоростью звука в этом газе, можно рассматривать среду как несжимаемую жидкость и для исследования движения потока применять уравнения, справедливые для несжимаемой жидкости с добавлением уравнения состояния газа. Ошибка, которую мы вводим в уравнение неразрывности, пренебрегая сжимаемостью газа, составляет менее 1%, если скорость движения газа не превышает примерно 1/7 скорости звука в неподвижной среде [27].
Средняя скорость движения газа в трубах электрофильтра у =- =- = 1,46 ж/сек, [c.42]
Скорость движения газов в трубах (приведенная к незаполненному объему) составляет w = 3,5 м/сек. [c.438]
Особые условия должны соблюдаться при сжигании на факелах ацетилена.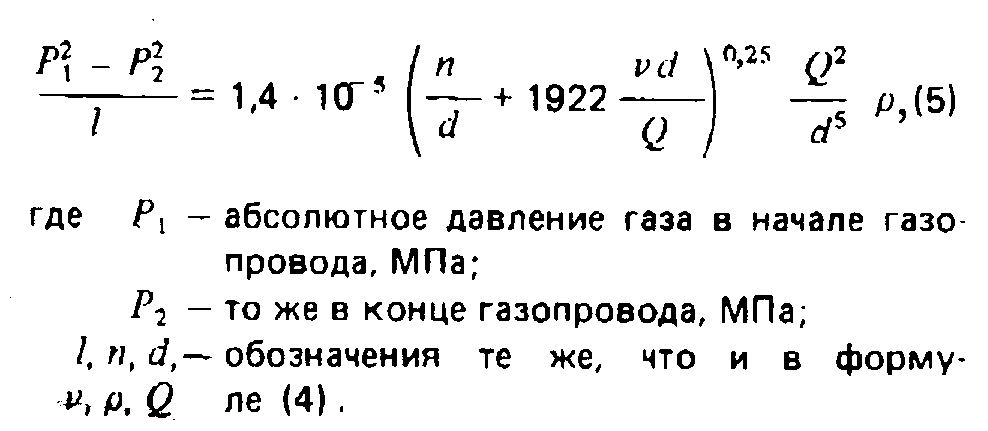
При сжигании ацетилена в среде воздуха скорость горения этого газа составляет около 3 м/с. Поэтому считают, что принимаемая скорость движения газа в трубе 5— 8 м/с соответствует условиям безопасного горения. Чтобы предотвратить образование застойных зон горючего газа в стволе периодически работающей факельной установки, его следует продувать азотом. В необходимых случаях перед факельным стволом на газопроводе устанавливают огнепреградители. Это позволяет предотвратить распространение пламени в факельные трубопроводы через ствол. Предварительно огнепреградители должны быть испытаны если при испытанни не было проскока пламени, то их можно устанавливать на трубопроводе. Огнепреградители обычно устанавливают в тех случаях, когда могут образоваться горючие смеси с нормальной скоростью распространения пламени с 0,45 м/с и для локализации взрывного распада ацетилена.
Скорость движения газа в трубе факела, г1езависимо от возможных колебаний нагрузки, всегда должна быть больше скорости распространения пламени, и в то же время — меньше некоторой предельной скорости, при которой в зможен отрыв пламени.
[c.133]
Сопротивление движущегося плотного слоя находят по формуле (Х,42). График AP=f(w) для рассчитываемых переточных устройств представлен на рис. 94. По графику определяют скорость движения газа в трубе переточного устройства 0,47 м/с для первого и 0,6 м/с для второго устройства. Принимая отношение Ртр1Ротв= 1,15, получают следующие скорости движения газа в отверстии переточных устройств 0,54 м/с для первого и 0,69 м/с для второго устройства. Определяют числа Архимеда для условий входа противоточного газа [c.218]
Аппарат представляет собэй вертикальную трубчатку, выполненную из алюминиевых труб диаметром 26/32 мя и длиной 7000 мм. Скорость движения газа в трубах 1=3,65 м/сек, скорость движения рассола в межтрубном пространстве 0)2=0.02 м сек. [c.458]
Аппарат представляет собой трубчатку вертикального тииа внутренний диаметр труб 26 мм., внешний 32 жи трубы алюминиевые, длина 7000-мж.. Скорость движения газа в трубах ге ] =3,65 м1сек.
Скорость движения газов в трубе-сушилке за.чисит от размера зерен высушиваемого угля и колеблется в пределах 10—40 м/сек. Процесс сушки кратковременный. Наиболее итенсивно влага удаляется [c.409]
Диаметр трубы-сушилки принимают в за-висимосги от производительности, крупности высушиваемого материала и скорости движения газов в трубе [c.410]
Скорость движения газов не должна сильно превышать скорость витания, так как это вызовет излишний раскод энергии и ненужное увеличение длины трубы. При сушке крупных частиц продукта (>10 мм) необходимо сильно увеличить скорость движения газов в трубе, вследствие чего сушка будет уже иеэкономичяой. [c.410]
Особенности расчета течения газа с большой скоростью в ступенчатых газопроводах
АННОТАЦИЯ
В статье предлагается подход к оценке течения газа в газопроводах с резким изменением внутренних размеров канала стрелково-пушечного вооружения при различных скоростных режимах..jpg)
ABSTRACT
The article proposes an approach to the evaluation of gas flow in pipelines with an abrupt change in the internal dimensions of the channel of small arms and cannon at various speeds. Analysis of pressure ratio in subsonic and in the supersonic region, given the turbulence of the gas and by varying the gas-dynamic functions allow to specify local losses in conventional weapons, using the criteria of similarity for flow of liquid. Theoretical justification of the methodology will at first, to more accurately simulate thermodynamic processes at high pressures, which is important for pipelines small arms and cannon. The studied parameters of the dynamics are confirmed and geometric, in particular by varying the section areas that can give great opportunities, for example for automatic control of pressure differentials in the dynamics of transient processes. It should also be noted that too much the introduction of various coefficients present in the classical works being taken away from accurate estimates of gas-dynamic processes, particularly in the areas of turbulence in the gas flow.
Во многих образцах автоматического оружия отвод порохового газа из канала ствола в рабочие камеры (газовые двигатели, газовые противооткатные устройства) производится через ступенчатые газопроводы с внезапным их сужением или внезапным расширением. Течение газа в трубах с внезапным изменением их сечения сопровождается диссипацией кинетической энергии газа – так называемыми гидравлическими потерями, приводящими к значительному изменению полного давления и дополнительному изменению параметров потока в зоне резкого перепада параметров его сечения. Поэтому в гидравлике внезапные изменения сечения называются местными сопротивлениями.
Внезапное сужение приводит к изменению секундного расхода газа, отводимого из канала ствола, который не будет равен расходу через простой цилиндрический газопровод того же сечения. Особое значение приобретает определение параметров газа после внезапного расширения, знание которых необходимо для правильного учета потерь на теплоотдачу, достигающих в длинных газопроводах (газовые буфера авиапушек, газовые двигатели винтовок, газовые экстракторы авиапушек) до 50-60% от величины поступающей в газопровод энергии.
В настоящее время расчет течения газа в ступенчатых газопроводах производится в квазистационарной постановке. Имеющиеся в литературе инженерные методы расчета течения газа при внезапном расширении, например, в [2,3] основаны либо на предельных случаях – равенство p3=р1 для дозвукового потока и p3=р2 для сверхзвукового потока после внезапного расширения, либо на чисто гидравлической постановке при p=const (формула Борда – Карно). Ни тот, ни другой случай, не имеют для течения газа достаточного физического и экспериментального обоснования, причем ошибки от применения той или иной гипотеза возрастают с увеличением скорости течения.
Между тем в имеющейся литературе опытные данные позволяют более точно и без существенного усложнения задачи рассчитать течение газа с внезапным изменением сечения.
Рисунок 1. Потеря давления газа
Рассмотрим физическую картину течения газа при внезапном расширении (рис.1). При внезапном расширении всегда имеется переходный участок длиной (6-10) диаметров, включающий в себя движущийся газ и застойную, вихревую зону. В общем случае давление на заплечики находится между значениями р2 и р1. При этом возможны два качественно различных случая. Если поток до внезапного расширения звуковой, то согласно закону обращения воздействий он будет замедляться, а давление газа возрастать. Тогда р1<р3<р2 и наружное противодавление будет влиять на течение только, когда оно больше расчетного давления р2. При этом всегда будет устанавливаться равенство р2=pн, не соответствующее расчетному значению р2.
Нетрудно видеть, что допущения p3=р1 приводит к снижению давления на заплечики, к уменьшению количества движения после расширения к завышению гидравлических потерь. Более обоснованным физически для дозвукового потока явилось бы допущение p3=р2. Если поток до внезапного расширения сверхзвуковой или критический, то при расширении его скорость должна возрастать, а давление падать, т.е. р1<р3<р2.
При наличии противодавления, когда pн>р2 может произойти подтормаживание сверхзвукового потока, сопровождающееся скачком уплотнения и повышением давления р2 до величины больше pн. Допущение p3=р2, иногда принимаемое в этом случае [3] приводит также к занижению давление на заплечики и к увеличению гидравлического сопротивления.
Таким образом, оба случая гарантируют завышение гидравлических потерь, а, следовательно, и возрастание энтропии.
Рассмотрим возможные случаи расчета течений с внезапным расширением сечения потока. Исходя из системы уравнений газодинамики, запишем выражения для отношения параметров до и после изменения параметров сечения.
В качестве одного из них возьмем закон обращения воздействия [1-5], который в данном случае при уравнении состояния
имеет вид
= (1)
где α,ρ,p-коволюм, плотность и давление газа;
R,T-универсальная газовая постоянная и температура газа;
M,a-число Маха и скорость течения газа;
-изменение скорости движения газа и площади поперечного сечения газопровода;
k-показатель адиабаты,
а гидравлические потери, вызванные вихреобразованием, записываются по формуле Вейсбаха
где ϛ-безразмерный коэффициент, характеризующий местные сопротивления.
При условии осреднения величин и М до и (далее, все параметры с чертой вверху-осредненные), решение уравнения (1) приводит к выражению
, (2)
в котором
= =1+
Из уравнений энергии, неразрывности, состояния имеем
= (3)
(4)
(5)
И, наконец, в качестве условия возрастания энтропии, воспользуемся отношением полных давлений
(6)
Система уравнений (2) – (6) справедлива, как для внезапного сужения, так и внезапного расширения, и позволяет в общем случае найти пять искомых параметров ρ2, p2, T2, M2, .
При α = 0 в уравнениях нужно принять .
Порядок решения системы зависит от способа задания потерь при внезапном изменении сечение потока [3-5].
1) Задано значение коэффициента ϛ.
В этом случае двумя приближением из уравнения (2) в первом приближении находим значением М2, а затем из уравнений (1) – (4) определяем Т2, ρ2, p2.
Уравнение (5) служит в качестве критерия правильности решения. Коэффициент потерь ϛ находится из экспериментальных данных, которые для случая внезапного расширения и с учетом числа Рейнольдса обрабатываются в виде
либо для развития турбулентного течения в виде [2]
Если принять степенной закон изменения скорости по течению трубы
,
то для круглой трубы при переменном значении радиуса трубы r имеем
При значений m=7, принятом в гидравлике, γ=1,06; β=1,02.
Из зависимости для коэффициента K следует отметить формулу Гибсона
= ,
полученную для 1,25 < d < 15 см.
Отметим так же, что все приведенные зависимости получены для жидкости применительно к течению порохового газа и нуждаются в экспериментальном уточнении. По-видимому, при течении газа с большой скоростью
2) Задано значение коэффициента потерь полного давления
В этом случае значением М2 находится из уравнения (6).
Данных по величинам коэффициента χ при внезапном расширении в литературе нет. Для внезапного сужения в первом приближении можно порекомендовать значения коэффициента χ, полученные для отвода газов из канала ствола и приведенные в таблице 1.
Таблица 1
Параметры отвода газов при внезапном сужении
|
λ1 |
0 |
0,2 |
0,4 |
0,5 |
0,6 |
0,8 |
|
χ1 |
0,76 |
0,72 |
0,64 |
0,58 |
0,53 |
0,48 |
3) Задано отношение
Это отношение было определено Уиком для случая критического истечения газа через плоский канал [1,6].
Экспериментальных данных для течения газа в круглых трубах нет, потому что данные по λ2 имеют довольно существенный разброс.
При задании отношения при расчете вместо управления (2) следует исходить из уравнения количества движения при расходе газа G, например, в виде
В заключении остановимся на определении числа М2 для внезапного расширения при критическом режиме истечения. Решение уравнения (2) или (6), при этом даст два значения – дозвуковое и сверхзвуковое. Формально следует брать сверхзвуковое решение. Однако сверхзвуковое решение не соответствует физике процесса, так как до расширения всегда имеется цилиндрический участок, скорость течения по которому вследствие теплоотдачи падает и становится дозвуковой.
Таким образом, приведенная методика позволяет вести расчет течения газа в газопроводах с внезапным истечением сечения при любых способах задания местного сопротивления. Однако коэффициент учета местных сопротивлений требуют экспериментального уточнения применительно к течению газа с большой скоростью.
Список литературы:
1. Абрамович Г.Н. Прикладная газовая динамика. – М.: Наука, 1976. – 888 с.
2. Дейч М.Е. Техническая газодинамика. – М.: Энергия, 1974. – 592 с.
3. Кулагин А.В. Газодинамический подход к оценке потерь на теплоотдачу в простом газопроводе // Инже-нерный вестник Дона, 2013, №2 / [Электронный ресурс]. – Режим доступа: URL: ivdon.ru/uploads/article/pdf/IVD_82_Kulagin.pdf_1736.pdf (дата обращения: 10.10.2016)
4. Кулагин В.И. Газодинамика автоматического оружия. – М.: ЦНИИ информации, 1985. – 256 с.
5. Лойцянский Л.Г. Механика жидкости и газа. – М.: Дрофа, 2003. – 840 с.
6. Черный Г.Г. Газовая динамика. – М.: Наука, 1988 – 424 с.
References:
1. Abramovich G.N. Applied gas dynamics. Moscow, Nauka Publ., 1976, 888 p. (In Russian).
2. Deitch M.E. Technical gas dynamics. Moscow, Energiia Publ., 1974 – 592 p. (In Russian).
3. Kulagin A.V. Gas-dynamic approach to assessing the loss on heat transfer in a simple gas pipeline. Inzhenernyi vestnik Dona [Engineering journal of Don], 2013, no. 2. Available at: URL: ivdon.ru/uploads/article/pdf/IVD_82_Kulagin.pdf_1736.pdf (accessed 10 October 2016).
4. Kulagin V.I. Dynamics automatic weapons. Moscow, TsNII informatsii Publ.,1985, 256 p. (In Russian).
5. Loytzyansky L.G. Mechanics of liquid and gas. Moscow, Drofa Publ., 2003, 840 p. (In Russian).
6. Cherny G.G. Gas dynamics. Moscow, Nauka Publ., 1988, p. 424 (In Russian).
1.5 Средняя скорость движения газа в газопроводе и суточная потеря газа при истечении его из отверстия в теле трубы.
Среднюю скорость движение газа определим по номограмме (рисунок 1.1) для следующих условий:
– среднее давление газа в трубопроводе Рср = 7,138 МПа;
– внутренний диаметр трубы Dвн=118,4 см;
–
расход
газа
.
По номограмме находим .
Согласно СТО Газпром 2-3.5-051-2006 скорость газа не должна превышать 20 м/с, данное требование выполняется.
Суточную потерю газа определим при эквивалентном размере образовавшейся неплотности 1 см2. Среднее давление газа в трубопроводе Рср=7,137 МПа, средняя температура Тср=295,19 К скоростью газа в трубопроводе пренебрегаем.
Критическое отношение давлений для газа (считаем газ – метан, показатель адиабаты k = 1,31)
(1.37)
Имеющийся перепад давлений больше критического, поэтому истечение газа происходит со скоростью равной местной скорости звука в газе.
Массовый секундный и массовый суточный расходы вытекающего газа
(1.38)
где показатель рода газа
(1.39)
Рисунок 1.1 – Номограмма для определения средней скорости движения газа
1.6 Охранные зоны магистрального газопровода.
Для исключения возможности повреждения трубопроводов (при любом виде их прокладки) устанавливаются охранные зоны. Размеры охранных зон и зон минимальных расстояний объектов МГ, порядок производства в этих зонах любого вида работ определены СТО Газпром 2-2.1-249, СНиП 2.05.06-85* и ВСН 51-1-80.
Рассматриваемый газопровод относится к I-му классу, имеет условный диаметр 1400 мм. Минимальные расстояния от оси газопровода до некоторых объектов представлены в таблице 1.6. Минимальные расстояния от компрессорных и газораспределительных станций данного газопровода до объектов представлены в таблице 1.7.
Таблица 1.6 – Минимальные расстояния от оси газопровода до объектов
Объекты, здания и сооружения | Расстояние, м |
Города и другие населенные пункты; отдельные промышленные и сельскохозяйственные предприятия; отдельно стоящие здания с массовым скоплением людей; железнодорожные станции; аэропорты; морские и речные порты и пристани | 350 |
Железные дороги общей сети (на перегонах) и автодороги I-III категорий, параллельно которым прокладывается трубопровод | 250 |
Отдельно стоящие нежилые и подсобные строения; устья бурящихся и эксплуатируемых нефтяных, газовых и артезианских скважин; автомобильные дороги IV, V, III-п и IV-п категорий, параллельно которым прокладывается трубопровод | 200 |
Кабели междугородной связи и силовые электрокабели | 10 |
Притрассовые постоянные дороги, предназначенные только для обслуживания трубопроводов | не менее 10 |
В охранных зонах трубопроводов запрещается производить всякого рода действия, могущие нарушить нормальную эксплуатацию трубопроводов либо привести к их повреждению, в частности:
перемещать, засыпать и ломать опознавательные и сигнальные знаки, контрольно-измерительные пункты;
открывать люки, калитки и двери необслуживаемых усилительных пунктов кабельной связи, ограждений узлов линейной арматуры, станций катодной и дренажной защиты, линейных и смотровых колодцев и других линейных устройств, открывать и закрывать краны и задвижки, отключать или включать средства связи, энергоснабжения и телемеханики трубопроводов;
устраивать всякого рода свалки, выливать растворы кислот, солей и щелочей;
разрушать берегоукрепительные сооружения, водопропускные устройства, земляные и иные сооружения (устройства), предохраняющие трубопроводы от разрушения, а прилегающую территорию и окружающую местность – от аварийного разлива транспортируемой продукции;
бросать якоря, проходить с отданными якорями, цепями, лотами, волокушами и тралами, производить дноуглубительные и землечерпальные работы;
разводить огонь и размещать какие-либо открытые или закрытые источники огня.
Таблица 1.7 – Минимальные расстояния от КС и ГРС газопровода до объектов
Объекты, здания и сооружения | Расстояние, м |
Города и другие населенные пункты; отдельные промышленные и сельскохозяйственные предприятия; отдельно стоящие здания с массовым скоплением людей; железнодорожные станции; аэропорты; морские и речные порты и пристани | 700 |
Мосты железных дорог общей сети и автомобильных дорог I и II категорий с пролетом свыше 20 м | 500 |
Железные дороги общей сети (на перегонах) и автодороги I-III категорий, параллельно которым прокладывается трубопровод | 350 |
Автомобильные дороги IV, V, III-п и IV-п категорий | 350 |
Отдельно стоящие нежилые и подсобные строения; устья бурящихся и эксплуатируемых нефтяных, газовых и артезианских скважин; автомобильные дороги IV, V, III-п и IV-п категорий, параллельно которым прокладывается трубопровод | 250 |
Лесные массивы пород: а) хвойных б) лиственных | 75 30 |
В охранных зонах трубопроводов без письменного разрешения предприятий трубопроводного транспорта запрещается: возводить любые постройки и сооружения, строить коллективные сады с жилыми домами, устраивать массовые спортивные соревнования, соревнования с участием зрителей.
В аварийных ситуациях разрешается подъезд к трубопроводу и сооружениям на нем по маршруту, обеспечивающему доставку техники и материалов для устранения аварий с последующим оформлением и оплатой нанесенных убытков землевладельцам.
уравнений расхода природного газа под высоким давлением | 2020-02-03
Существует множество уравнений для определения расхода в трубопроводах природного газа и падений давления, связанных с этими потоками, или наоборот. Наша цель – определить достоверность каждого уравнения относительно скоростей потока, с которыми может столкнуться инженер-сантехник.
Предыдущие статьи этой серии предполагают, что в качестве обычных материалов для трубопроводов используются стальные трубы сортамента 40 или полиэтиленовые трубы (PE).Внутренний диаметр каждой из этих труб разный. Кроме того, не существует стандарта, каким может быть давление на входе в эти трубы и каковы могут быть ожидаемые падения давления. Таким образом, не существует стандартизированных таблиц для условий более высокого давления, которое превышает давление, указанное в Национальном кодексе по топливному газу NFPA 54 и Международном кодексе по топливному газу ICC.
В результате, если проектировщик системы природного газа хочет подавать природный газ под давлением более 5 фунтов на кв. Дюйм, он / она может подготовить свои собственные таблицы, аналогичные таблицам в NFPA 54, но на основе более высокого давления и более высоких перепадов давления.
Для определения реальных уравнений потока использовалось несколько источников. (1) Соображения относительно уравнений установившегося потока в трубопроводах природного газа Пауло М. Коэльо и Карлос Пиньо в журнале Бразильского общества механических наук и инженерии, июль-сентябрь 2007 г .; (2) Crane Technical Paper 410 , 2018; (3) Глава 22 ASTM MNL 58 «Переработка нефти и переработка природного газа» , 2013 г., касающаяся Транспортировка сырой нефти, природного газа и нефтепродуктов .
Все эти тексты указывают на то, что уравнение Дарси-Вайсбаха, по-видимому, является наиболее точным методом определения падения давления, но этого метода избегали из-за сложности определения значения для «f» (коэффициент трения). Большинство альтернативных уравнений потока газа появились еще до появления современных компьютеров. Вычисление «f» включает итерационный процесс, поскольку квадратный корень из «f» является частью знаменателя в обеих частях уравнения для «f» .Уравнение Дарси-Вайсбаха выглядит следующим образом:
ч L = f ( ) (Уравнение 1)
Где: ч л = потеря напора газа в футах (метрах) жидкости – в данном случае газ
f = коэффициент трения – безразмерный
L = длина трубы в футах (метрах)
D = внутренний диаметр трубы, те же единицы, что и «L»
V = скорость газа в футах в секунду (метры в секунду)
г = гравитационная постоянная 32.2)
В основе уравнений потока AGA лежит значение « f », которое является функцией числа Рейнольдса. Классическое уравнение для числа Рейнольдса:
Re = σ V D / μ (Уравнение 2)
Где: σ = плотность газа
В = скорость газа
D = внутренний диаметр трубы
μ = динамическая вязкость – 7E-06 фунт / фут-сек (0.010392 сантипуаз)
Чтобы помочь в расчетах, когда плотность разбивается на уравнение закона идеального газа, а скорость разбивается как функция потока и плотности, а затем подставляется в классическое уравнение числа Рейнольдса, можно вывести следующее уравнение:
Re = 4 Q st 29 S g P st / (μ π D T st ) (Уравнение 3)
Где: Q st = Расход газа при стандартных условиях
29 = молекулярная масса воздуха, 28.9647 фунтов / фунт-моль (28,9647 г / гмоль)
S г = удельный вес природного газа
Pst = стандартное давление газа – 14,696 фунтов на кв. Дюйм (101,325 кПа)
μ = динамическая вязкость – 7E-06 фунт / фут-сек (0,010392 сантипуаз)
π = PI = 3,14159
D = внутренний диаметр трубы
= Универсальная газовая постоянная, 1545,349 фунта f фут / (фунт-моль ° R) [8314,41 Дж / (кмоль ° K)]
T st = Стандартная температура газа, 518.67 ° R (288,15 ° К)
(Примечание: число Рейнольдса «безразмерно», что означает, что все единицы в числителе и знаменателе должны быть отменены. Уравнения 2 и 3 не были скорректированы, чтобы включать единицы. Читателю потребуется использовать его / ее справочный материал, чтобы определить необходимые поправочные коэффициенты.)
Также обратите внимание, что число Рейнольдса в уравнении 3 не зависит от фактического давления и температуры газа. В уравнении 3 интересно то, что, если используются уравнения высокого перепада давления, значение « f » останется неизменным от входа к выходу участка трубы.
В 1960-х годах Американская газовая ассоциация (AGA) предложила уравнения AGA, в которых используется общее уравнение газа с упрощенными предельными формами уравнений Коулбрука Уайта. В газовых трубах встречаются три режима потока: ламинарный поток, частично турбулентный поток и полностью турбулентный поток. Формулы значений «f» для них следующие:
Ламинарный поток: f = 64 / Re для Re <2000-4000 (Уравнение 4)
AGA Частично турбулентный поток: 1/ = -2 log 10 (2.825 / (Re )) (Примечание 1 ниже) (Уравнение 5)
Полностью турбулентный поток AGA: 1/ = -2 log 10 (ε / (3,7 D)) (уравнение 6)
Примечание 1: Раньше значение 2,825 в уравнении 5 было 2,51 и является уравнением Коулбрука-Уайта, 1990 г.
Где: Re = Число Рейнольдса
f = коэффициент трения – безразмерный
ε = шероховатость внутреннего диаметра трубы, те же единицы, что и «D»
D = внутренний диаметр трубы
Согласно Коэльо и Пиньо и «Нефтепереработка и переработка природного газа», переход между частично турбулентным потоком и полностью турбулентным потоком происходит там, где результаты двух уравнений пересекаются; используется более высокое значение «f» .
При расчете падения давления в техническом документе Crane 410 указано, что, если давление на входе ( P 1 ) и давление на выходе ( P 2 ) являются следующими, эти обобщения могут быть сделаны: Расчетный перепад давления ( P 1 – P 2 ) составляет менее 10% от входного давления P 1 , разумная точность будет получена, если удельный объем (V = 1 / σ) Используемый в формуле основан на условиях P 1 или P 2 , в зависимости от того, какие из них известны.(2) Если расчетное падение давления ( P 1 – P 2 ) больше примерно 10%, но меньше 40% входного давления P 1 , приемлемая точность будет получена, если удельный объем, используемый в формуле, основан на средних условиях P 1 и P 2 . (3) Если рассчитанный перепад давления ( P 1 – P 2 ) превышает примерно 40% входного давления P 1 , то предлагаются другие формулы для высокого перепада давления.В качестве альтернативы можно было бы разбить длину трубы на несколько сегментов, которые удовлетворяют указанным выше условиям, используя выходное давление сегмента «1» в качестве входного давления для сегмента «2» и так далее. Имейте в виду, что давления « P 1 » и « P 2 » являются абсолютными давлениями, а не манометрическими давлениями.
Выполняемые процедуры
Чтобы сделать некоторые выводы относительно достоверности каждого из альтернативных уравнений, обсуждаемых ниже, в Excel и Visual Basic была создана программа для вычисления значения « f » с точностью до 5 значащих цифр для каждого потока. точку, а затем рассчитайте расход на основе имеющегося перепада давления, используя приведенные выше уравнения (с помощью формулы Дарси-Вайсбаха).Эти точки сравнивались с ответами, полученными при использовании каждого из альтернативных уравнений. После того, как набор результатов был собран для каждого альтернативного уравнения, общий пакет результатов сравнивался с ответами Дарси путем деления альтернативных результатов на ответы Дарси; по одному. Были собраны следующие статистические данные: минимальное отношение, максимальное отношение, среднее отношение и стандартное отклонение.
Сравнения проводились для каждого из следующих параметров: заданное давление на входе, заданное конечное давление, расстояние в футах, диаметр трубы (фактический) и шероховатость внутренней поверхности трубы (если она учтена).
Характеристики природного газа: В тех случаях, когда уравнения допускали ввод, было включено следующее: Удельный вес природного газа = 0,60. Вязкость природного газа = 7E-06 фунт / фут-сек или 0,010392 сантипуаз.
Диапазоны давления: на входе 2 фунта на кв. Дюйм при падении на 1 фунт / кв. Дюйм, на 3 фунта на кв. Дюйм при падении на 2 фунта на кв. Дюйм, на 5 фунтов на кв. Дюйм при падении на 3,5 фунта на кв. Дюйм, на 20 фунтов на кв. и 40 фунтов на кв. дюйм при падении на 4 фунта на кв. дюйм.
Расстояния: от 10 футов (3 метров) до 2000 футов (610 метров) с шагом, аналогичным NFPA 54 и IFGC.
Номинальные размеры трубы: от 0,5 дюйма (DN-15) до 6 дюймов (DN150), если это возможно.
Материалы труб: стальная труба Sch 40, труба из полиэтилена SDR 11, труба из полиэтилена SDR 13,5.
Используемые уравнения: уравнение NFPA / IFGC, уравнение Мюллера, уравнение Веймута, уравнение распределения IGT, уравнение Spitzglass-High Pressure и ручные уравнения AGA для пластиковых труб. Для трубопроводов более низкого давления также сравнивались значения в таблицах NFPA / IFGC. Для труб низкого давления рассматривалась только сталь, поскольку они, вероятно, будут установлены выше уровня земли.ПЭ, а также стальные трубы были рассмотрены для газа 20 фунтов на кв. Дюйм и 40 фунтов на квадратный дюйм. Обратите внимание, что все уравнения были изменены, чтобы обеспечить Q ч (расход в час) как функцию от P 1 и P 2 (давления на входе и выходе)
.Результаты
Для всех следующих уравнений, “Q h ” – расход в кубических футах в час, “P 1 “ – давление на входе, “P 2 “ – давление на выходе, “D « – внутренний диаметр трубы в дюймах,« S г »- удельный вес, а « L » – длина сегмента трубы в футах.Шероховатость внутренней поверхности трубы была оценена как 0,0018 дюйма для стали и 0,00006 дюйма для полиэтилена. Примечание. Число Рейнольдса было создано для каждого диапазона значений, чтобы читатель мог посмотреть на ту часть диаграммы Муди, где существуют эти потоки.
NFPA / IFGC Уравнение низкого давления (для 1,5 фунтов на кв. Дюйм и выше):
Q h = (D * {18,93 * [(P 1 2 -P 2 2 ) * Y / (Cr * L)] 0,206 }) (1/0 .381) (Уравнение 7)
Где: Y = 0,9992 для природного газа
Cr = 0,6094 для природного газа
Уравнение Мюллера:
Q ч = (2826 * D 2,725 ) / S г 0,425 * [(P 1 2 -P 2 2 ) / L)] 0,575 (Уравнение 8)
Уравнение Уэймута:
Q ч = (2034 * D 2.667 ) / S г 0,5 * [(P 1 2 -P 2 2 ) / L)] 0,5 (Уравнение 9)
Уравнение распределения IGT:
Q ч = (2679 * D 2,667 ) / S г 0,444 * [(P 1 2 -P 2 2 ) / L] 0,555 ( Уравнение 10)
Шпицгласс-Уравнение высокого давления:
Q ч = (3410 / S г 0.5 ) * [(P 1 2 -P 2 2 ) / L)] 0,5 * [D 5 / (1 + 3,6 / D + 0,03 * D)] 0,5 (Уравнение 11)
Руководство по эксплуатации пластиковых труб AGA
Дополнительные переменные: «T b », – «Стандартная температура» или 518,67 ° R, «P b » – «Стандартное давление» или 14,696 psia, «T» – температура газа в градусы R; 60 ° F или 519,67 ° R, используемое для этого анализа, «Sg» – это удельный вес природного газа (воздух = 1.0), 0,60 используется для этого анализа, «µ» – вязкость газа, 7,0E-06 фунтов м / фут-сек, используемая для этого анализа, «Z» – коэффициент сжимаемости газа, 1,0 для низкого давления газ, а «ε» – шероховатость поверхности трубы в дюймах (0,0018 для стали и 0,00006 для пластика).
Для частично турбулентного потока (поток ниже критического потока, где поток меняется на полностью турбулентный ):
Q h = D 2.667 * 664,3 * T b / P b * [(P 1 2 -P 2 2 ) / (T * L)] 0,555 * 1 / (S г 0,444 * µ 0,111 ) (Уравнение 12)
Для полностью турбулентного потока (для более высоких расходов):
Q h = D 2,5 * 469,2 * T b / P b * [(P 1 2 -P 2 2 ) / (S g * T * Z * L)] 0.5 * log 10 (3,7 * D / ε) (Уравнение 13)
Таблица 1: Для входного давления 2,0 фунта на кв. Дюйм (13,8 кПа-изб.) И перепада 1,0 фунт / кв. Дюйм (6,9 кПа-изб.) С использованием стальной трубы Schedule 40, размеры от ½ дюйма (DN-15) до 6 дюймов (DN-150). ). | ||||
Уравнение | Мин. Коэффициент | Максимальное соотношение | Среднее соотношение | Std Dev. |
NFPA / IFGC | 0,837 | 1,020 | 0,915 | 0,039 |
Мюллер | 0,998 | 1,686 | 1,344 | 0,178 |
Уэймут | 0.836 | 1,227 | 1,049 | 0,087 |
IGT Distribution | 0,983 | 1.476 | 1,258 | 0,130 |
Шпицгласс HP | 0,582 | 0.906 | 0,777 | 0,086 |
Таблица NFPA | 0,800 | 1,020 | 0,882 | 0,044 |
Примечание. Диапазон чисел Рейнольдса: от 4,1E + 03 до 2,9E + 06. | ||||
Таблица 2: Для 3.Входное давление 0 фунтов на кв. Дюйм (20,7 кПа-изб.) И перепад 2,0 фунтов на кв. Дюйм (13,8 кПа-изб.) При использовании стальной трубы Schedule 40, размеры от ½ дюйма (DN-15) до 6 дюймов (DN-150). | ||||
Уравнение | Мин. Коэффициент | Максимальное соотношение | Среднее соотношение | Std Dev. |
NFPA / IFGC | 0.826 | 1.024 | 0,918 | 0,043 |
Мюллер | 0,981 | 1,754 | 1,385 | 0,202 |
Уэймут | 0,824 | 1.209 | 1.023 | 0,089 |
IGT Distribution | 0,969 | 1,514 | 1,277 | 0,147 |
Шпицгласс HP | 0,573 | 0,855 | 0.757 | 0,086 |
Таблица NFPA | 0,826 | 1.024 | 0,914 | 0,043 |
Примечание. Диапазон чисел Рейнольдса: от 6,2E + 03 до 4,4E + 06. | ||||
Таблица 3: Для 5.Входное давление 0 фунтов на кв. Дюйм (34,5 кПа-изб.) И перепад 3,5 фунта на кв. Дюйм (24,1 кПа-изб.) При использовании стальной трубы Schedule 40, размеры от ½ дюйма (DN-15) до 6 дюймов (DN-150). | ||||
Уравнение | Мин. Коэффициент | Максимальное соотношение | Среднее соотношение | Std Dev. |
NFPA / IFGC | 0.824 | 1,032 | 0,920 | 0,047 |
Мюллер | 0,962 | 1,806 | 1,420 | 0,217 |
Уэймут | 0,809 | 1.159 | 0,999 | 0,092 |
IGT Distribution | 0,949 | 1,539 | 1,292 | 0,158 |
Шпицгласс HP | 0,536 | 0,836 | 0.739 | 0,086 |
Таблица NFPA | 0,785 | 1,003 | 0,885 | 0,386 |
Примечание. Диапазон чисел Рейнольдса: от 8.5E + 03 до 6.0E + 06. | ||||
Таблица 4: Для 20.Входное давление 0 фунтов на кв. Дюйм (137,9 кПа-изб.) И перепад 2,0 фунтов на кв. Дюйм (13,8 кПа-изб.) При использовании стальной трубы Schedule 40, размеры от ½ дюйма (DN-15) до 6 дюймов (DN-150). | ||||
Уравнение | Мин. Коэффициент | Максимальное соотношение | Среднее соотношение | Std Dev. |
NFPA / IFGC | 0.849 | 1,064 | 0,960 | 0,050 |
Мюллер | 0,992 | 1,665 | 1,253 | 0,151 |
Уэймут | 0,832 | 0.934 | 0,878 | 0,028 |
IGT Distribution | 0,980 | 1,363 | 1,139 | 0,088 |
Шпицгласс HP | 0,437 | 0,859 | 0.656 | 0,101 |
AGA Plast Pipe Manual | 0,990 | 1,042 | 0,997 | 0,003 |
Примечание: Диапазон чисел Рейнольдса: от 8,8E + 03 до 6,3E + 06 | ||||
Таблица 5: Для 20.Входное давление 0 фунтов на кв. Дюйм (137,9 кПа-изб.) И перепад 2,0 фунтов на кв. Дюйм (13,8 кПа-изб.) При использовании полиэтиленовой трубы SDR 13,5, размеры от 1 дюйма (DN-25) до 6 дюймов (DN-150). | ||||
Уравнение | Мин. Коэффициент | Максимальное соотношение | Среднее соотношение | Std Dev. |
NFPA / IFGC | 0.807 | 0,905 | 0,830 | 0,020 |
Мюллер | 0,996 | 1,578 | 1,309 | 0,151 |
Уэймут | 0,664 | 1.045 | 0,910 | 0,094 |
IGT Distribution | 0,978 | 1,359 | 1,177 | 0,117 |
Шпицгласс HP | 0,528 | 0,832 | 0.696 | 0,066 |
AGA Plast Pipe Manual | 0,989 | 1,033 | 1.000 | 0,011 |
Примечание. Диапазон чисел Рейнольдса: от 2,2E + 04 до 5,4E + 06. | ||||
Таблица 6: Для 20.Входное давление 0 фунтов на кв. Дюйм (137,9 кПа-изб.) И перепад 2,0 фунта на кв. Дюйм (13,8 кПа-изб.) При использовании полиэтиленовой трубы SDR 11 размером от 3/4 дюйма (DN-20) до 6 дюймов (DN-150). | ||||
Уравнение | Мин. Коэффициент | Максимальное соотношение | Среднее соотношение | Std Dev. |
NFPA / IFGC | 0.690 | 0,926 | 0,824 | 0,054 |
Мюллер | 0,909 | 1,523 | 1,254 | 0,143 |
Уэймут | 0,594 | 1.048 | 0,890 | 0,102 |
IGT Distribution | 0,836 | 1,345 | 1,151 | 0,125 |
Шпицгласс HP | 0,496 | 0,827 | 0.654 | 0,067 |
AGA Plast Pipe Manual | 0,845 | 1.026 | 0,978 | 0,045 |
Примечание. Диапазон чисел Рейнольдса: от 1,5E + 04 до 4,6E + 06. | ||||
Таблица 7: Для 40.Входное давление 0 фунтов на кв. Дюйм (275,8 кПа-изб.) И падение давления 4,0 фунта на кв. Дюйм (27,6 кПа-изб.) При использовании стальной трубы Schedule 40, размеры от ½ дюйма (DN-15) до 6 дюймов (DN-150). | ||||
Уравнение | Мин. Коэффициент | Максимальное соотношение | Среднее соотношение | Std Dev. |
NFPA / IFGC | 0.880 | 1,107 | 0,996 | 0,056 |
Мюллер | 0,985 | 1,802 | 1,352 | 0,169 |
Уэймут | 0,826 | 0.917 | 0,869 | 0,028 |
IGT Distribution | 0,987 | 1.442 | 1.201 | 0,098 |
Шпицгласс HP | 0,435 | 0,854 | 0.649 | 0,100 |
AGA Plast Pipe Manual | 0,998 | 1.011 | 0,990 | 0,001 |
Примечание. Диапазон чисел Рейнольдса: от 1,6E + 04 до 1,2E + 07. | ||||
Таблица 8: Для 40.Входное давление 0 фунтов на кв. Дюйм (275,8 кПа-изб.) И перепад в 4,0 фунта на кв. Дюйм (27,6 кПа-изб.) При использовании полиэтиленовой трубы SDR 13,5, размеры от 1 дюйма (DN-25) до 6 дюймов (DN-150) | ||||
Уравнение | Мин. Коэффициент | Максимальное соотношение | Среднее соотношение | Std Dev. |
NFPA / IFGC | 0.800 | 0,872 | 0,815 | 0,015 |
Мюллер | 0,998 | 1,621 | 1,337 | 0,158 |
Уэймут | 0,623 | 0.985 | 0,853 | 0,087 |
IGT Distribution | 0,970 | 1,365 | 1,174 | 0,118 |
Шпицгласс HP | 0,496 | 0,779 | 0.652 | 0,062 |
AGA Plast Pipe Manual | 0,981 | 1,032 | 0,996 | 0,013 |
Примечание. Диапазон чисел Рейнольдса: от 4,2E + 04 до 1,0E + 07. | ||||
Таблица 9: Для 40.Входное давление 0 фунтов на кв. Дюйм (275,8 кПа-изб.) И падение давления 4,0 фунта на кв. Дюйм (27,6 кПа-изб.) При использовании полиэтиленовой трубы SDR 11 размером от 3/4 дюйма (DN-20) до 6 дюймов (DN-150). | ||||
Уравнение | Мин. Коэффициент | Максимальное соотношение | Среднее соотношение | Std Dev. |
NFPA / IFGC | 0.800 | 0,888 | 0,821 | 0,018 |
Мюллер | 0,989 | 1,613 | 1,303 | 0,153 |
Уэймут | 0,618 | 0.983 | 0,847 | 0,088 |
IGT Distribution | 0,969 | 1,361 | 1,166 | 0,116 |
Шпицгласс HP | 0,464 | 0,778 | 0.623 | 0,068 |
AGA Plast Pipe Manual | 0,982 | 1,032 | 0,993 | 0,012 |
Примечание. Диапазон чисел Рейнольдса: от 2.7E + 04 до 9.4E + 06. | ||||
Прочие соображения
Еще одно соображение в этом обсуждении – максимальная скорость.Это было подробно рассмотрено в Руководстве по проектированию сантехники ASPE, том 3, глава 11, которое будет опубликовано весной 2020 года. Учитываются шум и эрозия. Максимальную фактическую скорость газа в 100 футов в секунду (30,5 метров в секунду) следует учитывать при давлении газа более 10 фунтов на кв. Дюйм (69,0 кПа-изб.).
Во всех проведенных вычислениях использовался удельный вес 0,6 . Это произошло потому, что все таблицы в NFPA 54 и IFGC основаны на 0.6 удельный вес. В Интернете удельный вес природного газа находится в диапазоне от 0,6 до 0,7 . В Справочнике по сжиганию в Северной Америке (3 rd , издание 1986 г.) удельный вес природного газа находится в диапазоне от 0,59 до 0,64. Более высокий удельный вес означает более высокую вязкость, более низкое число Рейнольдса и более высокое значение для « f ». Это означает, что перепад давления будет выше или пропускная способность трубы при определенном падении давления будет ниже.0,5 ; это равняется 1,04 (и приблизительно 1,06 , если рассматривать «f» ). Следовательно, перепад давления будет в 1,08 – 1,12 раз больше для пропускной способности при Sg = 0,65 удельной плотности.
Выводы
Уравнения и таблицы в NFPA и IFGC обеспечивают очень сопоставимые значения с уравнениями ASTM / AGA с использованием уравнения Дарси и формулы Колебрука-Уайта для «f». Этот анализ предназначен для новой чистой трубы. Чистая труба не повлияет на режим частично турбулентного потока, поскольку поток на поверхности трубы ламинарный. Инженеру следует рассмотреть возможность умножения любого потока в полностью турбулентном диапазоне на коэффициент эффективности 0,90–0,97.
Уравнение Веймута дает консервативные значения для расхода и более высоких перепадов давления, чем может быть на практике. Уравнение Шпицгласа-высокого давления даже более консервативно, чем уравнение Веймута.
Уравнения распределения Мюллера и IGT обеспечивают более высокие скорости потока и меньшие перепады давления, чем может быть на практике. В результате эти уравнения не рекомендуются для типичных водопроводных систем, где может использоваться более высокое давление.
Уравнения AGA в Руководстве по пластиковым трубам AGA обеспечивают очень сопоставимые значения с уравнениями AGA, использующими уравнение Дарси и формулу Коулбрука-Уайта для «f» .
При применении этих формул необходимо учитывать два последних момента: максимальная скорость и фактический удельный вес природного газа.Максимальная скорость газа 100 футов в секунду (30,5 метров в секунду) для минимизации шума и эрозии. Следует учитывать удельный вес природного газа, поскольку более высокий удельный вес приведет к более высоким перепадам давления или меньшей пропускной способности трубы при заданном падении давления.
Хотя эти уравнения использовались для определения грузоподъемности (Q h ) в этой статье, уравнения можно использовать для создания таблицы, такой как NFPA / IFGC, для целей проектирования. Затем уравнения можно изменить, чтобы создать расчет падения давления, который инженер может использовать для проверки результатов анализа.
Расчет расхода природного газа в трубопроводных сетях на основе уравнения Веймута нестационарного состояния
Основные моменты
- •
Мы разработали аналитическую модель, основанную на уравнении Веймута нестационарного состояния.
- •
Мы ввели «Коэффициент усиления (G)» как шкалу увеличения расхода газа в трубопроводе.
- •
Коэффициент усиления увеличивается для всех сетевых систем с предпочтением параллельной системы.
- •
Наши результаты полезны для инженеров, чтобы делать более точные прогнозы пропускной способности.
Реферат
Отсутствие внимания к неустойчивому состоянию в трубопроводных сетях приводит к значительной ошибке для исследователей газа. Наша работа направлена на восполнение этого пробела для последовательных, параллельных и замкнутых трубопроводных сетей на основе нестационарного уравнения Веймута. Для этого мы ввели «Коэффициент усиления» по мере увеличения расхода газа в трубопроводах.Наши результаты показали, что коэффициент усиления для последовательного постоянного потока зависит от отношения диаметра и длины (D 2 / D 1 , L 1 / L). Значение коэффициента усиления для нестационарного потока последовательно приближается к установившемуся потоку, пока не достигнет 1,97 через 500 ч для L 1 / L = 0,25 и D 2 / D 1 = 2,5. Основываясь на наших разработках, коэффициент усиления просто зависел от отношения диаметров для установившегося потока в параллельных системах. Согласно нашим результатам, значение коэффициента усиления для нестационарного потока стремится к установившемуся параллельному потоку, пока не достигнет 12.50 при соотношении диаметров 2,5 через 4000 ч. Для петлевых систем основными параметрами коэффициента усиления были доли петли и отношение диаметров. Кроме того, для всех соотношений диаметров происходит значительный рост коэффициента усиления для нестационарного потока, когда доля петель превышает 0,75. Основываясь на наших результатах, для доли петель, равной 0,75, коэффициенты усиления для установившихся и нестационарных потоков сходились к 1,94 для отношения диаметров, равного 2,5, через 200 ч. Судя по нашим результатам, параллельная система имеет значительное преимущество по сравнению с последовательными и замкнутыми системами, но требует больших затрат.Этот документ в качестве базового отчета призван помочь инженерам газовой отрасли проектировать более точные сети газопроводов.
Ключевые слова
Природный газ
Трубопроводная сеть
Нестабильный поток
Уравнение Веймута
Рекомендуемые статьиЦитирующие статьи (0)
Полный текст© 2016 Elsevier B.V. Все права защищены.
Рекомендуемые статьи
Ссылки на статьи
لــــية الهندســـــة »الصفحة غير موجودة.
لا يوجد تعليقات
اعلان ام نظرا لتزامن اجازات واعياد عديدة مسيحية (عيد القيامة)
لا يوجد تعليقات
علان نتائج مسابقة «عادة إحياء أثر» 10 января 2021 г.
لا يوجد تعليقات
لا يوجد تعليقات
لا يوجد تعليقات
مشروع Real Life احمد اقدم مشاريع اتحاد طلاب الجامعة الامريكية بالقاهرة اضغط هنا
لا يوجد تعليقات
مسابقة تطوير مصر للإبتكار КОНКУРС ИННОВАЦИЙ اضغط هنا
لا يوجد تعليقات
مبادرة تعليم اللغة الالمانية لطالب الجامعات المصرية اضغط هنا
لا يوجد تعليقات
الاعلان الموحد لخطه البعثات للعام الرابع 0202-0202 الجزء الثاني يشمل المبادره المصريه اليابانيه للJEP الي
لا يوجد تعليقات
لا يوجد تعليقات
ПРИЗЫВ УЧАСТНИКОВ ОНЛАЙН-ОБУЧЕНИЕ: Семинар по синим рабочим местам и сквозным навыкам для молодых специалистов и выпускников из Средиземноморских стран.14-15 апреля 2021 года пресса здесь
Расход и падение давления газа в трубопроводе
Расход и падение давления природного газа в трубопроводе
Существует несколько формул для расчета расхода, и для их правильного использования необходимо учитывать некоторые соображения:
- Они являются эмпирическими, что означает, что многие элементы в них являются константами или значениями, которые действительны в пределах определенного набора единиц и должны быть изменены при рассмотрении другого набора единиц.В этой статье мы используем британские единицы измерения; таким образом, эти формулы недействительны при использовании другого набора, например SI.
- Применимость этих формул была проверена в различных условиях. Было обнаружено, что некоторые из них дают более точные результаты с измеренными значениями в определенном диапазоне условий, чем другие. Итак, пользователь должен быть осторожен при выборе того, какой из них применить.
- Не учитывается разница в высоте между точками входа и выхода.Если такая разница существует, ее влияние на изменение давления требует изменения формулы (здесь не показано) или должно учитываться другими способами.
- Диапазон давления выше 100 фунтов на кв. Дюйм.
Для этих формул коэффициент сжимаемости можно рассчитать следующим образом:
- P 1 : Давление на входе, [psia]
- P 2 : Выходное давление, [psia]
- T 1 : Температура на входе, [° R]
- T 2 : Температура на выходе, [° R]
- S: Удельный вес газа, [безразмерный]
Мы будем использовать четыре уравнения, представленные GPSA (Ассоциацией поставщиков газоперерабатывающих предприятий):
• Weymouth.
• Panhandle A.
• Panhandle B.
• AGA (Американская газовая ассоциация).
Уравнение Веймута
Уравнение Веймута должно использоваться с учетом следующего:
• Точность результата снижается по мере увеличения турбулентности потока. Таким образом, это уравнение можно применять, пока число Рейнольдса (Re) меньше 2000. В случае более турбулентного потока (Re> 2000) следует использовать другие уравнения (Panhandle A, Panhandle B или AGA).
Уравнение:
- Q: Расход газа, [CFD], [кубических футов в день], [футов 3 / день] при базовых условиях.
- T b : Базовая температура, равная 520 [° R].
- P b : Базовое абсолютное давление, равное 14,76 [psia].
- E: КПД трубопровода, [безразмерный].
- L м : Длина трубопровода, [мили].
- d: Внутренний диаметр, [дюйм].
Уравнение Panhandle A
Panhandle Уравнение должно использоваться со следующими соображениями:
• Результаты этого уравнения показывают, что при использовании с коэффициентом эффективности E между 0.9 и 0,92 (0,9
Уравнение Panhandle B
Уравнение Panhandle B следует использовать с учетом следующих соображений:
• Результаты этого уравнения показывают, что при использовании E между 0,88 и 0,94 оно лучше приближается к полностью турбулентному потоку. Таким образом, он больше подходит для Re от 3000 до 4000.
Уравнение:
Уравнение AGA
Уравнение AGA следует использовать с учетом следующих соображений:
• Оно подходит для полностью турбулентного потока (Re> 4000).
Где
ε: Абсолютная шероховатость (фут).
| Материал | Абсолютная шероховатость (фут) |
|---|---|
| Тянутая латунь | 0,000005 |
| Тянутая медь | 0,000005 |
| Коммерческая сталь | 0.00015 |
| Кованое железо | 0,00015 |
| Асфальтированный чугун | 0,0004 |
| Оцинкованное железо | 0,0005 |
| Чугун | 0,00085 |
Поскольку Re зависит от скорости жидкости, определяемой ее расходом, невозможно узнать Re до тех пор, пока оно не будет вычислено, а это означает, что после вычисления Q следует проверить Re. Таким образом, принятый результат Q должен быть результатом формулы, Re которой попадает в ее диапазон.
Определение числа Рейнольдса:
и
и
где
Q с: расход, [фут 3 / сек] = Q / ((24) (60) (60))
V: скорость, [фут / сек]
D: диаметр, [дюйм] = d / 12
A: Площадь поперечного сечения, [футы 2 ]
: плотность газа, [фунт / фут 3 ]
: вязкость газа, [фунт / (фут * сек)]
Затем, выполняя замены с уже известными выше переменными:
, затем
и
В любом случае, важно отметить, что задействовано много эмпирических чисел, и результаты основаны на определенных предположениях, и нет такой точности, как с теоретически выведенным уравнением.Вот почему во многих практических применениях используется уравнение Веймута из-за его консервативного характера.
Расход газа в трубопроводе, CFD
Средняя температура, ° R
Коэффициент сжимаемости Zavg, (безразмерный)
Параметры числа Рейнольдса
Точность расчетаЦифры после десятичной точки: 3
Абсолютная шероховатость ε, ft Нарисованная латунь Нарисованная медьКоммерческая стальКованое железоАсфальтированное чугунОцинкованное железоЧугунcontent_copy Ссылка сохранить Сохранить расширение Виджет
Модифицированные модели расчета скорости утечки трубопроводов природного газа
Скорость утечки является важным параметром для оценки рисков и анализа отказов трубопроводов природного газа.Скорость утечки в трубопроводе природного газа следует рассчитывать быстро и точно, чтобы минимизировать последствия. Во-первых, в этом исследовании модели для оценки скорости утечки из трубопроводов природного газа реклассифицируются, а также анализируется теоретический диапазон применения каждой модели. Во-вторых, рассматривается влияние утечки на расход до точки утечки, и для реализации этого эффекта обратной связи изменения расхода используется метод последовательного приближения. Затем для расчета скорости утечки природного газа в этой статье разрабатывается модифицированная модель скважины.По сравнению со скоростью утечки, рассчитанной с помощью модели скважины-трубы, скорость утечки, рассчитанная с помощью модифицированной модели скважины-трубы, меньше и ближе к фактической скорости утечки из-за учета эффекта обратной связи при изменении скорости потока. Наконец, кривые скорости утечки модели скважины-ствола и модифицированной модели скважинной трубы при различных условиях d / D получены посредством моделирования. Результаты моделирования показывают, что модифицированная модель скважинного отверстия способна рассчитать скорость утечки любого отверстия утечки, такого как модель скважины-отверстия, а также с более высоким уровнем точности, чем модель скважины-отверстия.
1. Введение
Природный газ – это высококачественный, эффективный и чистый источник энергии. С 1970-х годов потребление природного газа во всем мире ускорилось, а исследования по эксплуатации, транспортировке и хранению природного газа также расширились, чтобы удовлетворить потребности [1–10]. Инфраструктура трубопроводов была возведена по всему миру для поддержки операций с природным газом. Огромная длина трубопровода, проложенного в самых разных условиях, неизбежно приводит к ускоренному повреждению трубопровода и отказу в определенных ситуациях.Международная статистика аварий на трубопроводах природного газа показывает, что искусственные повреждения, ошибки при строительстве, дефекты материалов и коррозия являются частыми причинами утечек в трубопроводах природного газа. Утечки могут привести к пожарам и даже смертельным взрывам; поэтому крайне важно быстро смягчить любые аварии на трубопроводе, чтобы уменьшить человеческие, экологические и корпоративные потери. Оценка скорости утечки из поврежденного газопровода – это первый шаг для прогнозирования площади, затронутой утечкой, и проведения любой необходимой эвакуации персонала.
Ввиду важности быстрого обнаружения и анализа утечек многие исследователи внесли свой вклад в разработку моделей утечек. Montiel et al. впервые предложил концепцию модели «отверстие-труба» и обсудил использование малых отверстий, больших отверстий и моделей трубопровода утечки в трубопроводе [11]. Чжоу проанализировал тепловой процесс медленной разгрузки резервуаров для хранения природного газа и создал соответствующую математическую модель [12, 13]. Вудворд и Мудан предложили идеальную модель утечки жидкости для небольших отверстий в компрессионных сосудах [14].На основе своей модели Центр безопасности химических процессов (CCPS) предложил несколько приблизительных формул для расчета скорости утечки при определенных условиях [15]. Young et al. предложила упрощенную модель расчета скорости утечки из малых отверстий газопроводов высокого давления с учетом запаса прочности, часто необходимого в практических ситуациях, и из-за запаса расчетные результаты были больше фактических [16, 17]. Arnaldos et al. выполнил простой анализ расчета скорости утечки как для модели трубы, так и для модели малого отверстия [18].Левеншпиль разработал модель утечки для случая полного разрыва трубопровода и проанализировал падение давления вдоль трубопровода. Однако модель была разработана на основе предположения, что давление в начальной точке остается постоянным, а поток газа и утечка в трубе являются адиабатическими процессами [19]. Донг рассчитал установившуюся утечку газа в магистральном трубопроводе [20]. Ян и др. установили стационарную модель утечки неизотермического трубопровода большой протяженности [21].
Из этих исследований можно сделать следующие выводы: Модели утечки обычно подразделяются на три типа: (1) модель малых отверстий, которую можно использовать для расчета скорости утечки небольших отверстий. Эта модель не только игнорирует трение вдоль трубопроводов, но также не учитывает влияние утечки на давление в трубопроводах. Поэтому погрешность этой модели велика, особенно когда точка утечки не мала. (2) Модель трубы для расчета скорости утечки в трубопроводе природного газа при полном разрыве трубопровода.Эта модель предполагает изоэнтропический выброс, а в начальной точке трубы предполагается постоянное давление. Учитывается перепад давления по трубе. Эта модель обеспечивает точные прогнозы для случая, когда трубопровод природного газа полностью разрушен, но ее нельзя применить к потоку через отверстия с диаметром меньше диаметра трубы. (3) Модель «скважина-труба», которая была впервые предложена Монтиелем и др., Затем стала краеугольным камнем месторождения. Теоретически эта широко используемая модель может рассчитать скорость утечки для различных отверстий.В этой модели учитываются трение вдоль трубопроводов и влияние утечки на давление в трубопроводах. Однако влияние утечки на скорость потока в трубопроводах природного газа не учитывается. Когда диаметр отверстия больше типичного диаметра малого отверстия и меньше диаметра трубопровода, ошибку все равно нельзя игнорировать.
На основе приведенного выше анализа в данной статье классифицируется исходная модель утечки. Кроме того, разработаны четыре новые модели для расчета скорости утечки: модель резервуара для хранения, модель малого отверстия, модифицированная модель трубы-отверстия и модель трубы.Подробно описаны характеристики каждой модели и конкретные условия их применения. Учитывая, как изменения расхода в трубопроводах природного газа могут вызывать явление обратной связи, в этой статье предлагается модифицированная модель скважинной трубы для расчета скорости утечки из различных отверстий, а также используется пример для проверки превосходства и рациональности моделей.
2. Реклассификация моделей расчета скорости утечки
В традиционной классификации модели расчета скорости утечки обычно делятся на три категории.В соответствии с реальными ситуациями в этой статье они классифицируются по четырем категориям и дается применимый объем каждой модели.
Анализируемая система схематически показана на Рисунке 1 [11]. Как показано на этом рисунке, имеется участок трубопровода L e , после которого имеется отверстие определенного диаметра, через которое происходит сброс давления.
Интересующие места включают точку 1 в начале трубы Точка 2 в центре трубопровода на той же вертикальной оси, что и точка утечки Точка 3, в точке утечки Точка 4, на внешней стороне труба, подверженная атмосферному давлению
Для расчета скорости утечки принимаются следующие гипотезы: (а) модель существенно одномерного потока; (б) изоэнтропический поток в точке сброса и адиабатический поток в трубе; и (c) газ ведет себя как идеальный газ.К уравнению состояния идеального газа добавляется коэффициент сжатия воздуха, чтобы уменьшить разницу с фактическим газом.
Применяя уравнения энергии и импульса к адиабатическому потоку через трубопровод, получается следующее уравнение [22]:
В этом выражении λ – коэффициент трения Фаннинга. Скорость утечки природного газа K в скважине может быть рассчитана с использованием следующего выражения, которое получается из уравнения неразрывности и закона идеальных газов для изоэнтропического расширения: где C D – поправка на поток. коэффициент утечки отверстия [23] и обычно устанавливается в диапазоне от 0.6 и 1.0. Этот коэффициент классифицируется в зависимости от формы отверстия. Если точная форма отверстия неизвестна, обычно рекомендуется консервативное значение 1,0. Это значение использовалось в данной статье [11].
Скорость потока в точке утечки зависит от того, является ли поток звуковым или дозвуковым, что можно определить по степени критического давления (CPR): где – критическое давление в точке 2. Если давление в точке 2 постепенно увеличивается, скорость утечки газа будет увеличиваться до тех пор, пока не сравняется с местной скоростью звука.В этот момент, если продолжает увеличиваться, то скорость утечки газа остается постоянной и всегда равна местной скорости звука и определяет критическую стадию потока.
Когда, то утечка критического потока была достигнута, и уравнение (4) подставляется в уравнение (2) для выражения утечки:
Когда утечка соответствует докритическому расходу, и утечку можно рассчитать по уравнению (2). Уравнения (2) и (4) представляют собой общие формулы для расчета скорости утечки природного газа.
В соответствии с различными, но приблизительными условиями, в данной статье устанавливаются модели утечки в трубопроводе природного газа (например, модель резервуара для хранения, модель малого отверстия, модифицированная модель трубы-отверстия и модель трубы). Эти четыре модели будут подробно описаны в следующем разделе.
2.1. Резервуар для хранения Модель
При протечке резервуара для хранения газа из-за большого размера резервуара можно сделать следующие приблизительные предположения: (a) утечка не влияет на давление внутри резервуара для хранения, а значения параметров в точке 2 остаются неизменными как до, так и после утечки.(b) Потери давления, вызванные трением между контейнером и потоком газа после утечки, не учитываются. В соответствии с этими двумя допущениями, параметры точки 1 используются для замены значения параметра точки 2, и скорость утечки может быть рассчитана по формулам (2) и (4), которые составляют модель резервуара для хранения. Эта модель широко использовалась для точного расчета утечки больших контейнеров, таких как резервуары для хранения [18].
Все эти аспекты делают эту модель пригодной для прогнозирования утечки через отверстие в резервуаре, но не для утечек в трубопроводах природного газа.Поскольку газопровод отличается от резервуара для хранения, особенно когда точка 2 находится далеко от точки 1, необходимо учитывать потерю давления и скорость, вызванные внутренним трением. Связанные параметры точки 2 не совсем такие же, как параметры точки 1. Скорость утечки, рассчитанная с помощью этой модели, больше, чем фактическая скорость утечки. Поэтому, как правило, модель резервуара для хранения не подходит для расчета скорости утечки природного газа в трубопроводе. Только когда точка 2 близка к точке 1 и диаметр отверстия очень мал, можно использовать модель резервуара для хранения для расчета скорости утечки из трубопроводов природного газа.
2.2. Модель малых отверстий
Модель малых отверстий используется для расчета скорости утечки в трубопроводе природного газа при небольших отверстиях. Эта модель учитывает эффект трения в трубопроводе природного газа. Поскольку утечка мала, влиянием утечки на давление и расход в трубопроводе природного газа можно пренебречь. Предполагая, что коэффициент трения одинаков на всем трубопроводе, связь между точкой 1 и точкой 2 может быть определена следующими уравнениями [11].где
В этих выражениях Ma – это число Маха, которое можно рассчитать следующим образом:
В этих условиях применяются следующие соотношения:
Когда в точке утечки существует критический поток, и скорость утечки может рассчитывается по уравнению (4).
Когда существует докритический поток в точке утечки, и скорость утечки можно рассчитать по уравнению (2).
Модель малого отверстия учитывает потерю давления, вызванную трением в трубопроводе природного газа, и является более точной, чем модель резервуара для хранения.Однако, поскольку модель малых отверстий не учитывает влияние утечки на давление и расход в трубопроводе природного газа, параметры в точке 2 остаются неизменными до и после утечки. Эта гипотеза все же отличается от реальной ситуации. Следовательно, только когда отверстие утечки очень маленькое, можно использовать модель малого отверстия для расчета скорости утечки.
2.3. Модель трубы
Модель трубы используется в случае полного разрыва газопровода или когда диаметр утечки близок к диаметру трубы.Состояние природного газа в трубе такое же, как если бы газ находился в атмосферных условиях. Согласно сохранению скорости потока, скорость утечки равна скорости потока в трубопроводе природного газа. Таким образом, формула для расчета скорости утечки природного газа имеет следующий вид [18]:
В это время, поскольку трубопровод полностью разорван, = =, и T 2 можно получить с помощью уравнения (6) . Модель дает хорошие прогнозы для случая полного разрушения трубопроводов природного газа, но не может быть применена к потоку через отверстия диаметром меньше диаметра трубопровода природного газа.
2.4. Модифицированная модель скважинной трубы
Перед тем, как представить модифицированную модель скважинной трубы, необходимо сначала представить модель скважины-трубы. В модели «скважина-труба» были учтены два аспекта: потеря давления, вызванная трением трубопровода, и влияние утечки на давление в трубопроводе. Однако влияние утечки на скорость потока перед местом утечки не учитывается.
В модели «скважина-труба» скорость утечки также рассчитывается по уравнениям (2) и (4).Уравнения (5) – (10) выражают взаимосвязь параметров между точками 1 и 2, и эти уравнения подставляются в уравнения (2) и (4), чтобы отразить учет потерь давления, вызванных трением в трубопроводе природного газа.
Для критического потока в отверстии точки утечки соотношение параметров между точками 2 и 3 определяется следующим образом:
Для докритического потока в отверстии точки утечки давления в точке 3 и окружающей среде одинаковы, поэтому соотношение параметров между точками 2 и 3 определяется следующим образом:
Уравнения (12) и (13) используются для расчета после возникновения утечки, и это может отражать влияние утечки на давление, но расчеты сложны.
Выше представлено основное введение в модель скважинной трубы.
Модифицированная модель «отверстие-труба», предложенная в этой статье, также используется для расчета скорости утечки газа, когда диаметр отверстия точки утечки больше, чем у модели малого отверстия. Поскольку диаметр отверстия и скорость утечки больше, учитывается влияние следующих двух аспектов: (a) Влияние утечки на давление в трубопроводе природного газа. Давление в точке утечки будет уменьшено после ее возникновения, и соответствующая скорость утечки изменится.Этот эффект учтен в модели скважины, но требует сложных расчетов. Этот эффект также учитывается в модифицированной модели скважины с отверстием, и метод последовательного приближения используется, чтобы избежать сложных расчетов. (B) Влияние утечки на расход до точки утечки. Согласно закону сохранения массы, расход до точки утечки должен быть равен сумме скорости утечки и расхода после точки утечки.Таким образом, скорость потока перед местом утечки изменится, что приведет к изменению давления в трубопроводе. Изменение давления дополнительно влияет на скорость утечки, которая, в свою очередь, влияет на скорость потока перед местом утечки. Эта серия событий действует как петля обратной связи. Влияние утечки на скорость потока перед точкой утечки будет распространяться на окрестности источника, и это не принимается во внимание моделью скважины-ствола, но учитывается в предлагаемой модифицированной модели скважины-ствола.
Для удобства расчета давление на конце трубы принято фиксированным значением. В этой модели для расчета скорости утечки природного газа используется метод последовательного приближения. Конкретные шаги следующие: (1) Расход до точки утечки Q – известен, а скорость утечки K и давление в точке 2 рассчитываются с помощью модели малого отверстия (2) Если>, то расход в трубе после точки утечки Q + может быть получен в соответствии с давлениями и.Согласно закону сохранения массы, расход газа в трубопроводе до точки утечки может быть получен с помощью Q – ‘= K + Q + ‘ и Q – ‘равно вставлено в шаг 1 для расчета новых K ‘и’. Этот процесс повторяется до тех пор, пока результаты расчета скорости утечки природного газа не будут стабильными. (3) Если ≤, то скорость потока природного газа в трубопроводе после точки утечки Q + равна 0.Согласно закону сохранения массы, может быть получено и вставлено в шаг 1 для расчета новых K ’и’. Этот процесс продолжается до тех пор, пока результаты расчета скорости утечки природного газа не станут стабильными.
Блок-схема модифицированной модели скважинной трубы показана на рисунке 2, где σ представляет собой пороговое значение.
С помощью описанных выше конкретных шагов можно обнаружить, что ‘и, полученные после цикла, неизбежно изменятся. Таким образом, следует учитывать влияние изменения ‘на состояние потока в трубе.Затем поток в отверстии точки утечки можно классифицировать как критический поток и докритический поток, и можно получить три состояния потока в трубопроводе и в отверстии: (a) Докритический поток в трубопроводе и критический поток в месте утечки. точечное отверстие На этом этапе формула для расчета скорости утечки с помощью модели малого отверстия на этапе 1 представляет собой уравнение (4) (b) Докритический поток в трубопроводе и подкритический поток в точке утечки В этой точке формула для расчета скорость утечки по модели малого отверстия на шаге 1 представляет собой уравнение (2) (c) Критический поток в трубопроводе природного газа и критический поток в точке утечки
На этом этапе формула для расчета скорости утечки с помощью небольшого Модель ствола скважины на этапе 1 представляет собой уравнение (4)
Аналогично, давление в точке 2, полученное в каждом цикле, должно выбираться, как описано выше.Модифицированная модель скважинной трубы учитывает влияние утечки на скорость потока в трубопроводе природного газа до и после точки утечки, что в большей степени соответствует реальной ситуации. Более того, метод итерационной аппроксимации, используемый в этой модели, позволяет избежать сложных математических выводов.
3. Сравнение моделей
Из-за легковоспламеняемости и взрывоопасности природного газа нецелесообразно проводить эксперименты по измерению скорости утечки на реальных газопроводах.Даже если для экспериментов используется сжатый воздух, трудно смоделировать несколько утечек с разным размером отверстий, чтобы получить разные значения d / D (отношение диаметра отверстия точки утечки к диаметру трубопровода). Поэтому в этой статье для сравнения моделей используются симуляции.
3.1. Введение в расчетный пример
Чтобы проверить эффективность моделей, особенно для сравнения модели скважины-трубы и модифицированной модели скважины-трубы, в данной статье эти модели применяются к следующим сценариям аварий.Параметры приведены в таблице 1.
| |||||||||||||||||||||||||||||||||
3.2. Обсуждение и сравнение
На основе предложенных выше моделей, а также параметров, взаимосвязь между скоростью утечки природного газа и d / D различных моделей в условиях устойчивого состояния показана на рисунке 3.Скорости утечки природного газа, рассчитанные по модели резервуара для хранения и модели с малым отверстием, быстро увеличиваются с увеличением d / D. Только когда d / D невелико, скорости утечки этих двух моделей близки к скорости утечки модифицированной модели скважинных труб, что соответствует сфере применения этих двух моделей. Модель резервуара для хранения может применяться только в том случае, если точка утечки находится очень близко к точке 1 трубопровода природного газа, а отверстие утечки очень мало. Из рисунка 3 также видно, что скорости утечки модифицированной модели скважинного ствола и модели скважинного ствола показывают одну и ту же тенденцию, причем обе они очень близки.Однако скорость утечки модифицированной модели скважинной трубы меньше, чем у модели скважинной трубы. Разница в скорости утечки при разных значениях d / D показана на рисунке 4. По мере увеличения d / D разница между этими двумя моделями сначала увеличивается, а затем уменьшается.
Когда отверстие утечки очень маленькое, можно применить модель малого отверстия. На диаграмме также показано, что скорость утечки природного газа, рассчитанная с помощью модели резервуара для хранения, больше, чем у модели с малым отверстием, что также согласуется с эффектом внутреннего трения модели с маленьким отверстием; поэтому модель малых отверстий более точна для расчета скорости утечки природного газа, чем модель резервуара для хранения.Поскольку происходит утечка, давление в точке 2 будет уменьшаться (но не будет уменьшаться бесконечно), в результате чего скорость утечки, рассчитанная с помощью модели «отверстие-труба», меньше скорости утечки, рассчитанной с помощью модели малого отверстия; но разница несущественная. Таким образом, при небольшом отверстии скорости утечки двух моделей очень близки. Когда отверстие увеличивается, влияние уменьшения давления в точке 2 на скорость утечки также увеличивается. Таким образом, скорость утечки не будет продолжать увеличиваться, а будет стремиться к плавной и устойчивой и в конечном итоге будет равна прогнозам модели трубопровода.
В случае реальной утечки, как только утечка происходит в определенной точке, расход (скорость потока) перед местом утечки должен увеличиться. Согласно уравнению Бернулли, давление потока будет уменьшаться с увеличением скорости потока. Этот эффект не учитывается в модели скважины; таким образом, скорость утечки, рассчитанная по модели скважины, больше, чем фактическая скорость утечки. Когда d / D мало, скорость утечки мала, изменение скорости потока небольшое, а давление в точке 2 испытывает минимальное изменение по сравнению с нормальным состоянием.Следовательно, эффектом обратной связи, обычно вызываемым утечкой, к давлению в трубопроводе перед местом утечки можно пренебречь. Однако по мере постепенного увеличения диафрагмы этой обратной связью нельзя пренебрегать. В модифицированной модели скважинной трубы, учитывая возникновение утечки в точке 2 (как показано на рисунке 1), скорость потока в трубопроводе перед точкой 2 будет увеличиваться, в то время как давление на входе уменьшается. В это время итерационная модель на рисунке 2 используется для расчета нового давления и скорости утечки в точке 2.Итерационная модель повторяется до тех пор, пока соответствующие параметры природного газа в трубопроводе после утечки не будут близки к реальной ситуации. Таким образом, скорость утечки, рассчитанная по этим параметрам, ближе к фактической скорости утечки, что объясняет, почему скорость утечки, рассчитанная с помощью модифицированной модели скважинного канала, меньше, чем скорость утечки, рассчитанная с помощью модели скважины с отверстием (Рисунок 3). С увеличением d / D размер отверстия увеличивается, а затем увеличивается скорость утечки. Кроме того, обратный эффект утечки на параметры газа (расход, скорость и давление) в трубопроводах становится все более очевидным, что увеличивает разницу в скорости утечки между модифицированной моделью трубного отверстия и моделью трубного отверстия.Когда d / D приближается к 1, размер отверстия приближается к диаметру трубопровода природного газа, а давление в точке 2 уменьшается и приближается к. Впоследствии формула скорости утечки превращается в уравнение (4), поэтому скорости утечки, вычисленные этими двумя моделями, в конечном итоге сходятся к стабильному значению вместе, еще больше уменьшая разницу. Это объясняет, почему разница сначала увеличивается, а затем уменьшается на Рисунке 4.
Скорость утечки природного газа, рассчитанная с помощью модели трубы, является прямой линией и не изменяется при изменении отверстия утечки.Модель трубы может применяться только в том случае, если диаметр утечки близок или равен диаметру трубопровода природного газа. Когда диаметр отверстия мал, скорость утечки газа модифицированной модели скважинной трубы очень близка к скорости утечки, рассчитанной с помощью модели резервуара для хранения или модели малых отверстий. По мере увеличения d / D скорость утечки природного газа быстро увеличивается, а затем медленно выравнивается. Когда отверстие утечки близко к диаметру трубопровода природного газа, скорость утечки, рассчитанная с помощью модифицированной модели скважины, совпадает со скоростью утечки, рассчитанной с помощью модели трубы.Этот результат показывает, что модифицированная модель скважинной трубы подходит для любого отверстия утечки.
На рисунке 5 показано соотношение между скоростью утечки природного газа K и L e (расстояние между точкой 1 и точкой утечки) модифицированной модели скважинной трубы (= 18 МПа) для различных d / D. По мере увеличения L e скорость утечки природного газа имеет нелинейную тенденцию к снижению. Эта тенденция к снижению обусловлена снижением давления, вызванным трением внутри трубопровода.Более того, разные отношения d / D утечки имеют разную степень серьезности. В частности, когда d / D мало, влияние утечки на параметры природного газа в трубопроводе невелико, и уменьшение скорости утечки происходит плавно. Когда утечка d / D уменьшается ниже определенной степени, влиянием утечки на параметры природного газа в трубопроводе можно пренебречь, и уменьшение скорости утечки природного газа становится незначительным. Когда утечка d / D увеличивается, кривая становится более пологой.На рисунке 6 показана взаимосвязь между K и d / D, предсказанная модифицированной моделью скважинной трубы (= 18 МПа) при различных L e . Из этого рисунка видно, что кривые скорости утечки под каждым L e аналогичны кривой скорости утечки, предсказанной модифицированной моделью скважинной трубы на рисунке 3. Рисунок 6 также показывает скорость утечки трубы. модель для каждого L e .Рисунок дополнительно подтверждает правильность модифицированной модели скважины-трубы. В то же время из рисунка видно, что скорость утечки уменьшается с л e . Когда d / D мало, скорость утечки уменьшается медленно, а по мере увеличения d / D скорость утечки уменьшается быстрее. Это согласуется с результатами, показанными на рисунке 5.
Рисунок 7 показывает взаимосвязь между K и (давлением в точке 1) модифицированной модели скважинной трубы ( л e = 1300 м) под разные д / д.Скорость утечки природного газа линейно увеличивается с увеличением. Кроме того, разные отношения d / D утечки приводят к разным уровням серьезности. Малое d / D приводит к минимальному увеличению скорости утечки из-за увеличения давления. И наоборот, большее значение d / D приводит к более высокой чувствительности между давлением и скоростью утечки. Это связано с тем, что, когда d / D мало, влияние утечки на параметры природного газа в трубопроводе невелико; когда d / D велик, это влияние велико. На рисунке 8 показано соотношение между скоростью утечки природного газа K и d / D модифицированной модели скважинной трубы ( L e = 1300 м) при различных значениях.Из этого рисунка видно, что кривые скорости утечки под каждой из них аналогичны кривой скорости утечки, предсказанной модифицированной моделью скважинной трубы на рисунке 3. Рисунок 8 также показывает скорость утечки модели трубы под каждой из них. Скорость утечки уменьшается по мере уменьшения. Когда d / D мало, скорость утечки уменьшается менее явно, а по мере увеличения d / D скорость утечки уменьшается более явно. Это согласуется с результатами на Рисунке 7. Вышесказанное дополнительно подтверждает модифицированную модель скважины.
Рисунки 5–8 дополнительно демонстрируют соответствие между параметрами уравнения (2) и уравнений (4) – (10). Соотношение между ‘и d (диаметр отверстия в точке утечки) показано на рисунке 9.
Согласно алгоритму модифицированной модели скважины и трубы, показанному в разделе 2.4, по мере увеличения d утечка скорость K увеличивается, и, следовательно, скорость потока (скорость потока) перед местом утечки должна увеличиваться из-за сохранения массы.Согласно уравнению Бернулли, давление потока уменьшается с увеличением скорости потока. Из того, что обсуждалось выше, ‘уменьшается по мере увеличения d , что согласуется с тенденцией, показанной на Рисунке 9. Кроме того, согласно уравнениям (12) – (14), до того, как’ упадет до, поток в точке утечки находится в состоянии критического потока. Как только ‘опускается ниже, поток в точке утечки становится докритическим. Точка разграничения между критическим потоком и докритическим потоком составляет около d = 195 мм.
4. Выводы
В этой статье модели утечки природного газа классифицируются на четыре типа. (а) Модель резервуара для хранения – в этой модели параметры природного газа считаются такими же, как параметры начальной точки, и при возникновении утечки изменений не происходит. Следовательно, эта модель применима к случаю, когда точка утечки находится близко к началу трубопровода, а диаметр точки утечки небольшой; (б) модель малого отверстия – в отличие от модели резервуара для хранения, эта модель учитывает влияние трения вдоль трубопровода природного газа, но предполагается, что давление в точке 2 остается постоянным после утечки.Следовательно, эта модель применима к случаю, когда диаметр точки утечки мал; (c) модель трубы – эта модель используется для случая полного разрыва трубопровода природного газа или когда диаметр точки утечки близок к диаметру трубопровода; и (d) модифицированная модель скважинного отверстия – эта модель является общей моделью, которая может рассчитывать скорость утечки при любом диаметре точки утечки.
Приведенные выше классификации более точно отражают реальную ситуацию. После определения размера точки утечки можно выбрать подходящую модель для оценки скорости утечки.Однако цель большинства проблем с утечкой в трубопроводе природного газа состоит в том, чтобы определить скорость утечки как можно раньше, и диаметр точки утечки не может быть известен заранее. Поэтому большую часть времени для оценки скорости утечки используется общая модель. В этом случае точность общей модели для расчета скорости утечки имеет решающее значение для оценки риска и анализа последствий отказа. В этой статье предлагается модифицированная модель скважинного отверстия, и инновации этой модифицированной модели заключаются в следующем: (1) с учетом влияния утечки на изменение скорости потока выше по потоку, изменение скорости потока приведет к изменению скорости потока.Согласно уравнению Бернулли, изменение скорости потока вызовет изменение давления, а изменение давления дополнительно повлияет на скорость утечки, что является проблемой контура. Это влияние не учитывается в модели скважины, но учитывается в этой модифицированной модели с помощью циклического итеративного алгоритма последовательного приближения. (2) В модели скважины учитывается влияние утечки на давление в точке утечки, но требуются сложные гидродинамические и термодинамические расчеты.В этой модифицированной модели скважинного трубопровода алгоритм итерационного цикла последовательного приближения может учитывать влияние утечки на давление в точке утечки и позволяет избежать сложных вычислений благодаря преимуществам алгоритма. Сравнение и анализ результатов расчетов в этой статье показывают, что модифицированная модель скважины-трубы, как и модель скважины-трубы, является общей моделью, которая может рассчитывать скорость утечки при любом диаметре точки утечки, а скорость утечки рассчитывается с помощью Модифицированная модель «отверстие-труба» ниже модели, рассчитанной с помощью модели «отверстие-труба», которая соответствует теоретическому анализу и должна быть ближе к фактической скорости утечки.Таким образом, предложенная в данной статье модифицированная модель скважинной трубы позволяет более точно рассчитать скорость утечки.
Номенклатура
| P : | Давление (Па) | ||
| : | Давление для каждой точки (Па) | ||
| : | Давление для окружающей среды (Па) | Критическое давление в точке 2 (Па) | |
| T : | Температура ( K ) | ||
| T i : | Температура в каждой точке (5 K) | ||
| u i : | Скорость потока (м / с) | ||
| G : | Массовый поток (кг / м 2 · с) | : | Коэффициент теплоемкости |
| Q : | Расход до точки утечки (кг / с) | ||
| Q + : | Расход после утечки p oint (кг / с) | ||
| K : | Скорость утечки в точке утечки (кг / с) | ||
| M : | Молярная масса (кг / моль) | ||
| : | Постоянная идеального газа (Дж / (моль.· K)) | ||
| X e : | Эквивалент между точкой 1 и точкой 2 (м) | ||
| D : | Внутренний диаметр труб (м) | ||
| Плотность газа (кг / м 3 ) | |||
| E : | Шероховатость труб (мм) | ||
| Re : | Коэффициент трения веером | ||
| A или : | Площадь отверстия (м 2 ) | ||
| C D : | Коррекция потока|||
| Z : | Коэффициент сжатия воздуха | ||
| CPR: | Степень критического давления | ||
| L e : | 9 0549 Расстояние между точкой 1 и точкой 2 (м)|||
| D : | Диаметр трубопровода (мм) | ||
| D : | Диаметр отверстия в точке утечки (мм). |
Доступность данных
Данные, использованные для подтверждения выводов этого исследования, можно получить у соответствующего автора по запросу.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Выражение признательности
Это исследование финансировалось научно-исследовательским проектом Харбинского коммерческого университета (№ 17XN013) под названием «Исследование по обнаружению и локализации утечек в трубопроводе природного газа на основе фильтра Калмана и оптоволоконного зондирования» и докторского исследовательского проекта Харбина. Университет коммерции (No.2016BS19).
Магазин AMPP – 09469 Скорость потока, необходимая для движения частиц в нефте- и газопроводах
Доступно для скачивания
Номер продукта: 51300-07108-SG
ISBN: 07108 2007 CP
Автор: ГРАММ.К. Мори, Дж. Хаберл, Дж. Фейерл, М. Оберндорфер, В. Хавлик, С. Хольцлейтнер
Дата публикации: 2007 г.
20,00 долл. США
Сожалеем, что-то пошло не так.Мы не можем завершить это действие. Пожалуйста, попробуйте еще раз позже.
Если эта ошибка продолжает возникать, обратитесь за помощью в первую службу NACE.
Используйте этот код ошибки для справки:
Пожалуйста, войдите, чтобы использовать кредиты стандартов NACE *
* Члены NACE получают зачетные единицы по стандартам NACE, чтобы использовать соответствующие стандарты и отчеты NACE в магазине.
Вы не являетесь членом NACE.
ЧленыNACE пользуются множеством преимуществ, в том числе кредитами стандартов NACE, которые можно использовать для погашения соответствующих требованиям стандартов и отчетов NACE в Магазине.
Вы можете посетить страницу членства в NACE, чтобы узнать о преимуществах членства в NACE.
Вы уже купили этот товар.
Перейдите в раздел «Загружаемые продукты» в своем профиле NACE Store, чтобы найти этот элемент.
У вас недостаточно кредитов NACE Standards для получения этого предмета.
Нажмите «ДОБАВИТЬ В КОРЗИНУ» , чтобы приобрести этот товар.
Ваш балл (-а) по стандартам NACE
Пожалуйста, проверьте свою транзакцию.
Нажмите «REDEEM» , чтобы использовать свои баллы по стандартам NACE для получения этого предмета.
Ваш балл (-а) по стандартам NACE
Вы успешно выкупили:
Перейдите в раздел «Загружаемые продукты» в профиле вашего магазина NACE, чтобы найти и загрузить этот элемент.
Доступно для скачивания
Номер продукта: 51300-10382-SG
ISBN: 10382 2010 CP
Автор: Грегор Мори, Томас Фогль, Иоахим Хаберль, Вольфганг Хавлик и Томас Шеберль
Дата публикации: 2010 г.
20 долларов.00
Сожалеем, что-то пошло не так.Мы не можем завершить это действие. Пожалуйста, попробуйте еще раз позже.
Если эта ошибка продолжает возникать, обратитесь за помощью в первую службу NACE.
Используйте этот код ошибки для справки:
Пожалуйста, войдите, чтобы использовать кредиты стандартов NACE *
* Члены NACE получают зачетные единицы по стандартам NACE, чтобы использовать соответствующие стандарты и отчеты NACE в магазине.
Вы не являетесь членом NACE.
ЧленыNACE пользуются множеством преимуществ, в том числе кредитами стандартов NACE, которые можно использовать для погашения соответствующих требованиям стандартов и отчетов NACE в Магазине.
Вы можете посетить страницу членства в NACE, чтобы узнать о преимуществах членства в NACE.
Вы уже купили этот товар.
Перейдите в раздел «Загружаемые продукты» в своем профиле NACE Store, чтобы найти этот элемент.
У вас недостаточно кредитов NACE Standards для получения этого предмета.
Нажмите «ДОБАВИТЬ В КОРЗИНУ» , чтобы приобрести этот товар.
Ваш балл (-а) по стандартам NACE
Пожалуйста, проверьте свою транзакцию.
Нажмите «REDEEM» , чтобы использовать свои баллы по стандартам NACE для получения этого предмета.
Ваш балл (-а) по стандартам NACE
Вы успешно выкупили:
Перейдите в раздел «Загружаемые продукты» в профиле вашего магазина NACE, чтобы найти и загрузить этот элемент.
Доступно для скачивания
Номер продукта: 51318-11594-SG
Автор: Тереза Люнг / Дженни Бен / Янник Борегар / Джеймс Чоу
Дата публикации: 2018 г.
20 долларов.00
Сожалеем, что-то пошло не так.Мы не можем завершить это действие. Пожалуйста, попробуйте еще раз позже.
Если эта ошибка продолжает возникать, обратитесь за помощью в первую службу NACE.
Используйте этот код ошибки для справки:
Пожалуйста, войдите, чтобы использовать кредиты стандартов NACE *
* Члены NACE получают зачетные единицы по стандартам NACE, чтобы использовать соответствующие стандарты и отчеты NACE в магазине.
Вы не являетесь членом NACE.
ЧленыNACE пользуются множеством преимуществ, в том числе кредитами стандартов NACE, которые можно использовать для погашения соответствующих требованиям стандартов и отчетов NACE в Магазине.
Вы можете посетить страницу членства в NACE, чтобы узнать о преимуществах членства в NACE.
Вы уже купили этот товар.
Перейдите в раздел «Загружаемые продукты» в своем профиле NACE Store, чтобы найти этот элемент.
У вас недостаточно кредитов NACE Standards для получения этого предмета.
Нажмите «ДОБАВИТЬ В КОРЗИНУ» , чтобы приобрести этот товар.
Ваш балл (-а) по стандартам NACE
Пожалуйста, проверьте свою транзакцию.
Нажмите «REDEEM» , чтобы использовать свои баллы по стандартам NACE для получения этого предмета.
Ваш балл (-а) по стандартам NACE
Вы успешно выкупили:
Перейдите в раздел «Загружаемые продукты» в профиле вашего магазина NACE, чтобы найти и загрузить этот элемент.
Как очистить трубопровод природного газа газовыми ударами
Перед вводом в эксплуатацию вновь установленных трубопроводов и клапанов для природного газа, системы должны быть должным образом очищены для удаления потенциально повреждающих посторонних материалов, которые по своей природе остаются во время строительства. Этот процесс сложнее, чем может показаться, и требует точных расчетов силы очистки и подробных этапов последовательности действий для удаления всего мусора. Вот как это сделать правильно.
Перед тем, как новый трубопровод топливного газа можно будет подсоединить к турбине внутреннего сгорания (ТТ), его необходимо очистить продувкой «декомпрессионного» газа.
Процесс
Очищаемая труба подсоединяется одним концом к резервуару с газом. Это может быть резервуар или передняя часть чистого пустого трубопровода. На другом конце устанавливается временная выхлопная труба и клапан. Резервуар находится под давлением менее половины расчетного. Когда продувочный клапан быстро открывается, сжатый газ резко устремляется через трубопровод и выходит из выхлопной трубы (рис. 1).
1. Здесь показана типичная конфигурация компонентов газового трубопровода. Предоставлено: Michael F. Czyszczewski, PE |
Когда газ движется по трубе, мусор и жидкости собираются и выдуваются. Когда давление в резервуаре понижается до уровня, при котором очистка больше не происходит, клапан закрывается. Затем процесс повторяется снова и снова (от 10 до 100 раз), пока труба не будет признана чистой.
Если доступен достаточно большой компрессор, трубы малого диаметра (менее 4 дюймов) или трубы небольшой длины можно альтернативно очистить методом «непрерывной продувки». Это может ускорить процесс за счет исключения циклов повышения давления.
Какой газ использовать?
Первым выбором для очистки газа было использование рабочего газа. Однако после того, как в 2010 году произошел смертоносный взрыв при использовании природного газа, промышленность пересмотрела эту практику.Комиссия по химической безопасности (CSB), расследующая аварию, рекомендовала не использовать природный газ для очистки труб. CSB также призвал руководящий кодекс и организации по стандартизации запретить использование горючего газа и опубликовать инструкции по очистке с использованием альтернативных газов.
В ответ Национальная ассоциация противопожарной защиты (NFPA) выпустила NFPA 56 «Стандарт по предотвращению пожаров и взрывов во время очистки и продувки систем трубопроводов горючего газа» в предварительной форме в 2011 году и окончательной форме в 2013 году.Этот стандарт запрещает использование горючего газа для очистки труб, если расчетное давление в системе превышает 125 фунтов на квадратный дюйм. В 2011 году Исследовательский институт электроэнергетики (EPRI) выпустил «Руководство по очистке топливных газопроводов сжатым воздухом или азотом». Эти альтернативные газы можно сравнить следующим образом:
- Воздух. Воздух должен быть чистым, сухим и обезжиренным. Для продувки газом, вероятно, потребуются более высокие давления и потоки, чем те, которые доступны от компрессоров инструментального воздуха станции.При необходимости можно арендовать более крупные компрессоры или несколько компрессоров, чтобы получить необходимое давление и скорость потока. Также могут потребоваться такие аксессуары, как воздушный ресивер, предохранительные клапаны, регуляторы и осушители воздуха.
- Азот. Химически инертный азот обычно используется для продувки и обеспечения защиты от коррозии для оборудования топливного газа. Азот негорючий, невзрывоопасный, сухой и не содержит масел. Азот действительно представляет собой потенциальный риск удушья, который необходимо устранить, если он используется.Газ можно добывать на месте в больших объемах (от 3000 стандартных кубических футов в минуту [scfm] до 15000 scfm) и при очень высоких давлениях (до 15000 фунтов на квадратный дюйм) с помощью арендованных самосвалов, первоначально разработанных для использования в нефтегазовой отрасли. . Эти грузовики содержат приборы, резервуары для хранения, насосы, жидкий азот, испарители, предохранительные клапаны и другое оборудование, необходимое для подачи сжатого газа.
Экономия воздуха и азота может быть очень похожей. Выбранный вами газ должен соответствовать требованиям вашего проекта.
В своем выпуске 2016 года Кодекс трубопровода B31.1 Американского общества инженеров-механиков (ASME) пояснил, что он не предоставляет руководство по методам очистки труб, но добавил в своем выпуске 2018 года, что очистка трубопровода топливного газа может осуществляться в соответствии с требованиями NFPA 56. Стандарты NFPA часто принимаются федеральным, государственным или местным законодательством.
Когда труба чистая?
Полированная металлическая пластина, известная как «мишень», вставляется в газовый тракт, где она будет поражена частицами мусора во время подачи газа.Чистота труб зависит от количества и размера ударов частиц, разрешенных производителем СТ. Удары продолжаются до тех пор, пока проверка двух последовательных планшетов не покажет больше баллов, чем допускается критериями приемки.
Мишень должна быть установлена на временной выхлопной «выхлопной трубе» как можно ближе к очищаемому сегменту трубы, чтобы предотвратить ложные показания цели из-за обломков, возникающих во временной трубе. Он должен располагаться вдали от возмущений потока, создаваемых коленами и тройниками, а не на выходе из трубы, где должна быть ударная волна.Мишень должна быть как можно меньше, чтобы минимизировать падение давления. Пластины из твердого металла будут иметь меньше ударов, поэтому материал, конструкция и расположение цели должны быть согласованы с владельцем и производителем ТТ.
Большая часть очистки происходит во время первого раунда продувки газа. По мере очистки цвет шлейфа разряда будет меняться с ржаво-оранжевого на прозрачный. Мишень можно вставлять только после того, как будет проведена значительная очистка.
Какой трубопровод очищается газовыми ударами?
Производители определяют, как следует очищать впускной газовый трубопровод к их оборудованию.Газовые удары в основном выполнены на трубопроводе подачи газообразного топлива с выхода счетчика службы газа на входы запорного клапана на КТ. Если после узла кондиционирования топливного газа используется трубопровод из нержавеющей стали, его можно вместо этого визуально осмотреть с помощью бороскопа. При обнаружении мусора нержавеющую трубу следует очистить струйной очисткой или щеткой в зависимости от условий.
Если трубопровод газового оборудования не соответствует заданному критерию чистоты, его все же можно очистить продувкой газа.Используются нецелевые «служебные удары», и очистка продолжается до тех пор, пока шлейф выхлопных газов не станет прозрачным. Одним из примеров является трубопровод топливного газа к канальным горелкам парогенератора-утилизатора. Вместо этого другие вторичные системы, такие как трубопровод подачи газа к вспомогательному котлу, можно подвергнуть химической очистке или струйной очистке с последующей технологической продувкой.
Продувка газом некоторых сложных трубопроводов может оказаться непрактичной. Вместо этого короткую труднодоступную трубу можно очистить гидролазированием (струей воды под высоким давлением).
Определение путей удара
Длина трубопровода, который можно очистить при продувке газом, ограничена. Для гидравлического сопротивления и расположения запорных клапанов и ответвлений обычно требуется несколько путей потока. Для подготовки и настройки каждого пути потребуется время и ресурсы. Определение оптимальных путей продувки имеет решающее значение для эффективного процесса и, следовательно, требует тщательного рассмотрения, чтобы свести к минимуму количество необходимых продувок.
Процесс определения путей продувки называется «секционированием».«Схема трубопроводов и приборов (P&ID) должна быть изучена и отмечена, чтобы показать направление и траекторию для каждого запланированного удара. На этой схеме должно быть показано расположение предлагаемого источника газа, целевой пластины, продувочного клапана, запорных клапанов, инструментальных клапанов, выхлопной трубы и всех временных соединений с постоянной трубой.
На диаграмме также должны быть указаны любые салазки оборудования, сопла, диафрагмы и тепловые колодцы, которые следует удалить, заменить деталями золотника или обойти, чтобы предотвратить их повреждение или исключить падение давления, которое они могут вызвать во время продувки газом.Если клапан не может быть удален, он должен быть полностью открыт во время ударов и время от времени закрываться и открываться между ударами, чтобы встряхивание удалило любые частицы, которые могли попасть в клапан. Ниже приведены некоторые советы по определению путей удара:
- Путь всегда должен начинаться от источника газа, рассчитанного на ожидаемое давление продувки и имеющего достаточный объем для обеспечения разумного времени продувки. Этим источником может быть автоцистерна с азотом, изолируемая секция уже очищенной восходящей трубы или арендованный сосуд высокого давления.
- Путь должен заканчиваться временным выпускным отверстием выхлопной трубы. Для некоторых путей продувки может потребоваться переместить выхлопную трубу. В качестве альтернативы можно использовать дополнительные выхлопные трубы.
- Длинные пути продувки имеют высокое сопротивление потоку, и их следует избегать. Высокое сопротивление потребует более высокого пластового давления и использования большего количества продувочного газа.
- Грязный канал продувки не должен попадать в участок трубы, очищенный ранее.
- Пути продувки можно прокладывать в обратном направлении относительно нормального направления потока.Иногда это необходимо, когда объем резервуара перед очищаемой трубой недостаточен, но имеется достаточный объем ниже по потоку, который можно было бы использовать.
- Должна быть возможность изолировать путь потока. При необходимости можно установить временные клапаны или очковые фланцы для перекрытия ответвления. Следует избегать тупиковых (застойных) сегментов трубы, так как они могут захватывать мусор.
продувочный клапан
Продувочный клапан имеет решающее значение для успешной очистки. В закрытом состоянии, удар клапан используется в качестве запорного клапана, чтобы позволить вверх по течению трубопровода и резервуар, чтобы находиться под давлением.При открытии запускает процесс очистки газом. Самое главное, чтобы клапан мог быстро открываться. Более быстрый клапан позволит большему количеству очищающего газа очистить внутреннюю часть трубы с максимальной скоростью. Шаровой кран на четверть оборота или шиберная задвижка, открывающаяся за 0,5–1 секунду (или лучше), являются хорошим выбором. Из соображений безопасности предпочтительнее использовать автоматический привод.
Чем ближе клапан к выхлопной трубе; тем больший объем будет доступен выше по потоку для повышения давления. Больший объем дает больше энергии и более длительные удары.В качестве альтернативы размещение клапана перед очищаемым трубопроводом обеспечит дополнительный эффект очистки, когда клапан открывается и сжатый газ ударяет по грязной трубе. Однако, что наиболее важно, клапан следует устанавливать вдали от перебоев потока, а если используется ручной клапан, он должен находиться в доступном и безопасном месте.
Поскольку продувочный клапан будет подвергаться высоким напряжениям, нагрузкам и попаданию мусора, его можно легко повредить. Поэтому иметь запасной считается хорошей страховкой.
Вместо продувочного клапана иногда используются разрывные диски. Они одноразовые и открываются очень быстро. Однако, поскольку их необходимо заменять после каждого удара и они изготовлены с расчетом на одно заданное давление разрыва, они могут не подходить, когда требуется много продувок газа или пусковых давлений.
Расчет очистки
Принцип очистки газовой продувкой заключается в создании высоких скоростей газа и сил сопротивления, которые будут сдвигать обломки с внутренних стенок трубы.Эта чистящая сила (CF) определяется следующим образом:
CF = (m B 2 x v B ) / (2 x g c x A)
где m B – массовый расход продувочного газа во время очистки, v B – удельный объем продувочного газа во время очистки, g c – гравитационная постоянная, а A – площадь в хвостовой части. выход трубы. (Все переменные в уравнениях, упомянутых в этой статье, используют общепринятые единицы измерения США, такие как футы, секунды., фунт, фунт / кв.дюйм и F, если не указано иное.) CF во время продувки газом должен быть больше, чем максимальный CF во время работы для эффективной очистки. Другими словами, отношение очистки к рабочему CF, известное как коэффициент очищающего усилия (CFR), должно быть больше 1,0, как рассчитано по следующему уравнению:
CFR = CF B / CF M ≥ 1
, где CF B – чистящая сила удара, а CF M – максимальная чистящая сила во время работы.Обеспечение CFR больше 1,0 – это фундаментальный критерий, на котором основывается начальное давление газовой продувки. Опыт показал, что сила сопротивления от CFR, превышающая или равная 1,2, дает приемлемые результаты. Более высокие значения CFR не показывают значительно более быструю очистку и не рекомендуются, потому что выбрасывается больше газа. Однако следует использовать более высокий запас CFR, если этого требует производитель оборудования.
CFRувеличивается по мере продвижения вниз по трубе постоянного диаметра, поэтому для большей части трубы CFR будет во много раз больше 1.0. Кроме того, в расчетах не учитывается динамический удар, возникающий при внезапном открытии продувочного клапана. Из-за этого консерватизма минимальный CFR 1.0 считается разумным и достаточным для служебных ударов.
Для расчета CFR необходимы массовый расход и удельный объем на всем пути продувки. Происходят изменения звуковой и дозвуковой скоростей, закупорки потока и плотности, что затрудняет расчеты. К счастью, программное обеспечение для измерения расхода сжимаемой жидкости значительно упрощает работу.
Во-первых, постройте программную модель системы в ее нормальной рабочей конфигурации. Затем используются прогоны каждого рабочего режима для нахождения наибольших значений, соответствующих членам знаменателя уравнения CFR.
Затем измените модель, чтобы включить в нее любые изменения конфигурации, которые будут внесены для очистки. Все временные трубы, байпасы, выхлопная труба, продувочный клапан и запорные клапаны продувочного тракта должны быть добавлены.
Цель состоит в том, чтобы использовать модель для определения начального и конечного давлений в резервуаре продувочного газа, которые приведут к приемлемым значениям CFR по всей длине очищаемой трубы.Это делается методом проб и ошибок, в ходе которого проверяются различные давления, а результаты измерения массового расхода и удельного объема импортируются в электронную таблицу, которая рассчитывает CFR. Ниже приведены некоторые рекомендации по определению начального давления:
- По мере сброса давления в трубе (продувки) скорость газа будет уменьшаться. Когда давление источника падает до точки, где CFR ниже 1,0, подачу газа можно прекратить. Не полностью сбрасывая давление, можно минимизировать время рециркуляции и количество используемого газа.Однако будьте осторожны. Если время продувки очень короткое (менее 10 секунд), полная разгерметизация даст больше времени для выброса мусора.
- Увеличение массового расхода газа или удельного объема увеличивает CFR. Массовый расход можно увеличить за счет увеличения пластового давления. Удельный объем можно увеличить за счет уменьшения давления в трубе или повышения температуры.
- Когда газ течет по трубе, давление на пути падает из-за трения.Падение давления приводит к увеличению удельного объема и скорости газа. Если достигается скорость звука, образуется ударная волна. Скорость больше не будет увеличиваться за пределами ударной волны, и поток считается «забитым». Звуковое перекрытие может происходить в местах, где диаметр трубы внезапно увеличивается, на выходе из трубы и в местах сужений, таких как клапан с уменьшенным внутренним диаметром. В идеале звуковое дросселирование должно происходить только на выходе из трубы, а не внутри трубы, где это может вызвать сильные вибрации трубы.
- Увеличение диаметра выхлопной трубы увеличивает CFR. Однако диаметр выхлопной трубы не должен быть больше диаметра трубопровода, с которым она соединяется, чтобы избежать образования внутренней точки сужения.
Приборы для измерения давления и температуры с возможностью записи данных, установленные рядом с впускным и выпускным отверстиями для газа, должны использоваться для подтверждения того, что достигаются приемлемые CFR. Используйте таблицу или диаграмму свойств газа, чтобы получить удельный объем на основе измеренных давления и температуры.Исследования показали, что наиболее надежным методом определения массового расхода (m B ) является расчет скорости звука (c) на выходе.
м B = A x c / v B
, где c – √ (kxg C x 144 x P E xv B ), k – отношение удельной теплоемкости (около 1,4 для воздуха и азота), а P E – давление в газе. выход.
Контроль шума
Удары газа громкие.Фактически, звуковые ударные волны могут быть видны в газовом шлейфе, выходящем из выхлопной трубы. Всем, кто работает поблизости, потребуется защита слуха.
Уровень звукового давления (SPL) указывает на интенсивность звука в данной точке по отношению к опорному уровню. Измерения обычно выражаются в единицах дБ (А), где «А» обозначает корректировку частотной чувствительности человеческого слуха. Исходя из предельного уровня шума в 90 дБ (A) Управления по охране труда (OSHA), рекомендуется снижение до уровня менее 85 дБ (A) на расстоянии 3 фута.SPL можно оценить с помощью следующего выражения, полученного из стандарта 521 Американского института нефти (API):
.SPL ≅ 20 log (d E /1000) – 10 log (v B ) + 80 log [(4 xv B xm B ) / (π xd E 2 )] – 10 лог (2 x π xr 2 ) – 22,232
, где d E – внутренний диаметр выхода газа из выхлопной трубы, а r – расстояние от выхода трубы. Если завод находится рядом с жилым районом, понадобится глушитель.При выборе глушителя потеря давления при максимальном расходе должна быть ограничена не более чем примерно 1 фунт / кв. Дюйм. Высокое сопротивление потоку приведет к более высокому давлению обдува и использованию большего количества продувочного газа.
Расчет времени и массы
Когда начинается разгерметизация, перепад давления между резервуаром и атмосферой высокий, а выходящий поток имеет звуковую скорость. По мере уменьшения разницы скорость на выходе остается постоянной до тех пор, пока не будет достигнуто критическое давление, и оно не станет дозвуковым.По мере дальнейшего снижения пластового давления объемный расход и массовый расход падают до тех пор, пока перепад давления не достигнет нуля. Время продувки (t BD ) можно оценить с помощью следующего эмпирического выражения, рекомендованного Американской газовой ассоциацией (AGA):
т BD ≅ (0,1225 x P 1 0,333 x S G 0,5 x V x F c ) / d E 2
, где P 1 – начальное давление газового резервуара, S G – удельный вес относительно воздуха (1.0 для воздуха и приблизительно 1,0 для азота), V – объем хранилища под давлением (включая бак, резервуар и трубопровод), а F C – коэффициент дросселирования (1 для идеального выхода до 1,8 и выше для типичного затвора. клапан). Убедитесь, что время продувки значительно больше времени открытия продувочного клапана и давление в резервуаре не превышает номинальное давление компонентов.
Компрессор прямого вытеснения заполняет резервуар с относительно постоянной скоростью потока.Время пополнения резервуара (t CHARGE ) можно оценить с помощью следующего выражения:
т ЗАРЯД ≅ [V x (P 2 – P 1 ) x 60] / (P a x Q)
, где P 2 – конечное давление газового резервуара, P a – атмосферное давление (14,7 фунт / кв. Дюйм), а Q – выходная мощность компрессора для заполнения резервуара. Чтобы оценить количество календарных дней, необходимых для очистки, необходимо количество ударов, необходимое для каждого пути продувки.
К сожалению, точное предсказание практически невозможно. Число может варьироваться от 1 до 100. Если был сделан акцент на «чистоту», потребуется меньше циклов продувки. Какое бы число ни использовалось, это будет приблизительная оценка, поэтому добавьте маржу. Дополнительное время следует добавить на сбор и проверку данных приборов, расчет CFR, удаление и вставку мишеней и осмотр мишени.
Нехватка азота во время очистки задержит ее завершение.Чтобы оценить количество азота, необходимое для продувки газа (q GAS ), используйте следующие выражения, основанные на законах идеального газа:
q ГАЗ ≅ (2,7 x S G x P 1 x V) / T
, где T – температура газа по шкале Ренкина (F + 459,67), или:
q ГАЗ ≅ V / v B
Испытания под давлением
ASME B31.1 охватывает проектирование и испытания систем трубопроводов электростанций. ASME B31.3 используется для промышленных трубопроводов, например, на нефтеперерабатывающем или химическом заводе.ASME B31.8 применяется к трубопроводам для транспортировки и распределения газа. Владелец установки должен определить, какие коды использовать и где они применяются.
Перед проведением продувки газом трубопровод необходимо испытать на герметичность. Обычно используется вода. Однако, если это разрешено правилами трубопроводов, вместо этого можно проводить пневматические испытания с использованием очищающего газа. Это может быть желательно в ситуациях, когда вода для гидроиспытаний не может быть легко удалена, недопустима в трубе или недостаточно доступна.
Применимый код трубопроводов описывает процесс проведения испытания пневматическим давлением. ASME PCC-2 дает метод определения расстояния, охватывающего трубу, которое следует обозначить предупреждающей лентой и очистить от людей. Решение о проведении пневматического испытания не следует воспринимать легкомысленно. Разрывы пневматических труб происходят внезапно, обычно без предупреждения; поэтому пневматические испытания не рекомендуются.
Разрядная сила
Подобно тяге ракетного двигателя, открытый выпуск создает статическую силу реакции на выходе из выхлопной трубы.Обычно требуется анкер, чтобы удерживать выхлопную трубу от движения. API RP 520-2 предоставляет следующее выражение, которое можно использовать для оценки осевой силы на выходе из выхлопной трубы (F):
F = 9,836 x m M x √ {(k x T) / [(k + 1) x M wt ]} + [144 x (P E – P a ) x A]
, где m M – массовый расход газа при максимальной работе, а M WT – молекулярный вес газа (около 28,5 для воздуха и азота).Когда продувочный клапан внезапно открывается, труба подвергается динамическим нагрузкам, поскольку газ начинает течь. Динамические силы учитываются коэффициентом динамической нагрузки (DLF). Этот коэффициент представляет собой отношение максимального напряжения от быстро приложенной нагрузки к напряжению, которое могло бы возникнуть при медленном приложении. DLF колеблется от 1,1 до 2,0. Обычно используется DLF, равный 2. Если требуется более низкое значение, см. Подробности в ASME B31.1.
Делай работу правильно
В исследовании, проведенном CSB в 2010 году по очистке газовой продувкой, около половины респондентов заявили, что у них нет технической базы для определения потоков и давления газа, которые они должны использовать.Без дополнительных расчетов, вероятно, потребуется больше времени и газа для очистки. Аналитический подход к очистке продувкой газа поможет обеспечить безопасное и эффективное протекание процесса.
В спорте «провал» – это когда одна команда превосходит другую с большим отрывом.