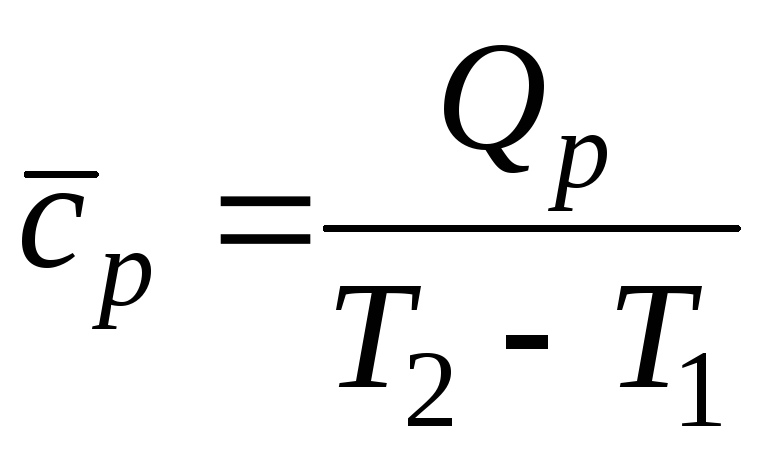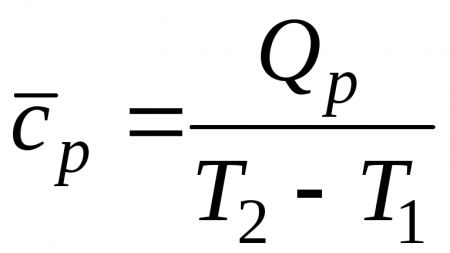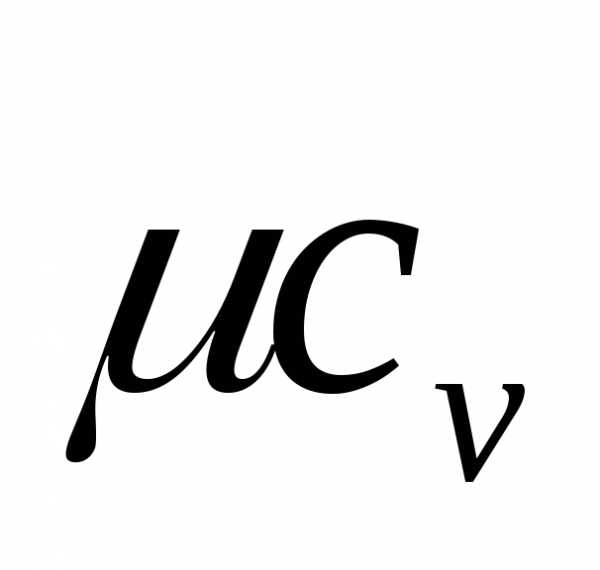2.2.Средняя и истинная теплоёмкости
Учитывая, что теплоемкость непостоянна, а зависит от температуры и других термических параметров, различают истинную и среднюю теплоемкости. Истинная теплоемкость выражается уравнением (2.2) при определенных параметрах термодинамического процесса, то есть в данном состоянии рабочего тела. В частности, если хотят подчеркнуть зависимость теплоёмкости рабочего тела от температуры, то записывают её как , а удельную – как. Обычно под истинной теплоёмкостью понимают отношение элементарного количества теплоты, которое сообщается термодинамической системе в каком-либо процессе к бесконечно малому приращению температуры этой системы, вызванному сообщенной теплотой. Будем считатьистинной теплоёмкостью термодинамической системы при температуре системы равной, а- истинной удельной теплоёмкостью рабочего тела при его температуре равной. Тогда среднюю удельную теплоёмкость рабочего тела при изменении его температуры отдоможно определить как
(2.6) |
Обычно в таблицах приводятся средние значения теплоемкости для различных интервалов температур, начинающихся с. Поэтому во всех случаях, когда термодинамический процесс проходит в интервале температур отдо, в котором, количество удельной теплотыпроцесса определяется с использованием табличных значений средних теплоемкостейследующим образом:
. | (2.7) |
Значения средних теплоемкостей и, находят по таблицам.
2.3.Теплоёмкости при постоянном объёме и давлении
Особый интерес представляют средние и истинные теплоемкости в процессах при постоянном объеме (изохорная теплоемкость, равная отношению удельного количества теплоты в изохорном процессе к изменению температуры рабочего тела dT) и при постоянном давлении( изобарная теплоемкость, равная отношению удельного количества теплоты в изобарном процессе к изменению температуры рабочего тела dT).
Для идеальных газов связь между изобарной и изохорной теплоёмкостями и устанавливается известным уравнением Майера .
Из уравнения Майера следует, что изобарная теплоемкость больше изохорной на значение удельной характеристической постоянной идеального газа. Это объясняется тем, что в изохорном процессе () внешняя работа не выполняется и теплота расходуется только на изменение внутренней энергии рабочего тела, тогда как в изобарном процессе () теплота расходуется не только на изменение внутренней энергии рабочего тела, зависящей от его температуры, но и на совершение им внешней работы.
Для реальных газов , так как при их расширении исовершается работа не только против внешних сил, но и внутренняя работа против сил взаимодействия между молекулами газа, на что дополнительно расходуется теплота.
В теплотехнике широко применяется отношение теплоемкостей , которое носит название коэффициента Пуассона (показателя адиабаты). В табл. 2.1 приведены значениянекоторых газов, полученные экспериментально при температуре 15 °С.
Таблица 2.1 | |
Газ | Показатель адиабаты |
Гелий | 1,660 |
Аргон | 1,667 |
Окись углерода | 1,401 |
Кислород | 1,398 |
Водород | 1,408 |
Азот | 1,41 |
Водяной пар | 1,33 |
Углекислый газ | 1,305 |
Аммиак | 1,313 |
Метан | 1,315 |
Теплоемкости изависят от температуры, следовательно, и показатель адиабатыдолжен зависеть от температуры.
Известно, что с повышением температуры теплоёмкость увеличивается. Поэтому с ростом температурыуменьшается, приближаясь к единице. Однако всегда остается больше единицы. Обычно зависимость показателя адиабаты от температуры выражается формулой вида
, |
где – значение коэффициента при 00С;- коэффициент, принимающий для каждого газа своё постоянное значение.
Кроме того, можно установить следующие широко использующиеся зависимости.
, | (2.8) |
и так как
. | (2.9) |
studfiles.net
Теплоемкость средняя – Справочник химика 21
С —средняя удельная теплоемкость — средняя молярная теплоемкость. [c.193]Если известно выражение зависимости Ср или Ср от температуры, то нетрудно вычислить из истинной теплоемкости среднюю и наоборот. [c.55]
Из таблицы теплоемкость средняя С=С(рср, Тз). [c.288]
Иногда применяют среднюю теплоемкость. Средней молярной теплоемкостью (С) в интервале температур от Т до Тч называют такую теплоемкость, которая равна отношению количества теплоты ((5), полученного 1 моль вещества, к приращению температуры (Л ). В данном интервале температур [c.31]
Из уравнений (И,33) и (П,34) видно также, что удельная (или киломольная) теплоемкость вещества равна тому количеству тепла, которое надо подвести к одному килограмму (или одному киломолю) вещества при данных условиях, чтобы повысить температуру его на один градус. В зависимости от того, при каких условиях производится нагревание или охлаждение вещества(при постоянном объеме или постоянном давлении), различают следующие виды теплоемкостей средние удельные изобарная (Ср) и изохорная ( j теплоемкости истинные удельные изобарная (Ср) и изохорная ( j теплоемкости соответственно средние и истинные киломольные изобарные (Ср, Ср) и изохорные (с , j теплоемкости. Эти теплоемкости связаны между собой определенными соотношениями. [c.66]
С = 0,4825 -f 0,000385 ([c.175]
Теплоемкость угля линейно возрастает с повышением его влажности и снижением степени метаморфизма зольность понижает теплоемкость. Среднюю удельную теплоемкость С при обычной температуре можно определить по формуле [c.53]
При изменении температуры в интервале от и до Ь следует брать значение теплоемкости, среднее для данного интервала-.
Поскольку теплоемкость веществ зависит от температуры, то различают среднюю и истинную теплоемкости. Средняя молярная теплоемкость системы С определяется как частное от деления количества тепла Q, затраченного на нагревание 1 моля вещества, на разность температур АТ, в пределах которых производилось нагревание [c.226]
Удельная теплоемкость средняя, кДж/(кг-К) 1,91/2,12 [c.107]
Удельная теплоемкость средняя между 16 и 260° — 0,0725 [c.384]
Газообразные продукты сгорания ТРТ и воспламенителя имеют одинаковые удельную теплоемкость, среднюю молекулярную массу и отношение теплоемкостей 7. [c.89]
Теплоемкость. Средняя удельная теплоемкость аморфного титана в зависимости от температуры характеризуется следующими цифрами [208] [c.247]
Энергия и теплоемкость. Средняя энергия, приходящаяся на одну молекулу, равна [c.383]
Удельная теплоемкость средняя между 16 и 260 Энтропия (на 111,6 г РЬО) при 298,1 . … Теплота образования, ккал/моль…… [c.505]
Интегрируя это выражение от температуры стандартных условий (25° С) до заданной температуры Т и заменяя истинную молекулярную теплоемкость средней (в пределах 298° К — Т° К), из уравнения (108 а) получаем [c.254]
Интегрируя это выражение от температуры стандартных условий (25°С) до заданной температуры Т и заменяя истинную мольную теплоемкость средней (в пределах от 298°К до Г°К), из уравнения (108-а) получи.м [c.187]
Теплоемкость. Средняя удельная теплоемкость аморфного бора в различных интервалах температур приведена ниже. [c.202]
Теплоемкость. Средняя удельная теплоемкость железа в различных интервалах температур имеет значения [24]
Если формула, выражающая зависимость Ср или Ср от температуры, известна, то нетрудно вычислить из истинной теплоемкости среднюю и наоборот. Из уравнений (47) и (48) следует, что [c.233]
Наименование материалов Объемный вес в слежавшемся состоянии в кг/м Коэффициент теплоемкости (средний) в ккал/ кг°С Коэффициент теплопроводности при 30 с в ккал/ мч°С [c.181]
Теплоемкость. Средняя удельная теплоемкость ванадия чистотой 99″/о между 20 и 100° определена равной 0,120 кал/г-°С. [c.344]
Теплоемкость. Среднюю удельную теплоемкость тантала при низких температурах характеризуют следующие значения [c.363]
Теплоемкость. Средняя удельная теплоемкость молибдена для некоторых интервалов температур составляет [c.454]
Теплоемкость. Средняя удельная теплоемкость рутения в интервале О—100°С равна 0,061 кал г (1. [c.646]
Определяющая роль фононной (решеточной) проводимости позволяет применить для качественного описания процессов передачи тепла уравнение Дебая, уточненное введением поправок на пористость и текстуру Х= АСрМ (е) f (К ), где X – теплопроводность Ср — теплоемкость / – средний свободный пробег фЬнонов V – скорость распространения упругих колебаний i e), / Ку) – факторы, учитывающие пористость и текстуру А — геометрический фактор. [c.109]
Наименованне изделий Теплопроводность средняя (Я, р) в ккал/м-ч°С Теплоемкость средняя (С ,р)в ккал/ кгч°С [c.183]
Теплоемкость. Средняя удельная теплоемкость вольфрама в интервале температур 19—100° составляет 0,0358, а истинная удельная теплое1Мкссть ири обыкновевкюй температуре найдена равной 0,0323 0,5 кал/г [c.473]
Теплоемкость. Средняя удельная теплоемкость металлического селена в интервале температур 15—217° составляет 0,078 кал1г-°С. [c.520]
Теплоемкость. Средняя удельная теплоемкость никеля в интервале температур 22 —1° характеризуется следующихмн цифрами [c.622]
Теплоемкость. Средн
www.chem21.info
2.7.Зависимость теплоёмкости от температуры. Истинная и средняя теплоёмкости.
Опытные значения теплоёмкостей при различных температурах представляются в виде таблиц, графиков и эмпирических функций.
Различают истинную и среднюю теплоемкости.
Истинная теплоемкость C-это теплоемкость для заданной температуры.
В инженерных расчетах часто используется среднее значение теплоемкости в заданном интервале температур (t1;t2).
Средняя теплоемкость обозначается двояко: ,.
Недостаток последнего обозначения является незаданность диапазона температур.
Истинная и средняя теплоемкости связаны соотношением:
(81)
Истинная теплоемкость-это предел, к которому стремится средняя теплоемкость, в заданном диапазоне температур t1…t2, при ∆t=t2-t1
Как показывает опыт, у большинства газов истинные теплоемкости возрастают с ростом температуры. Физическое объяснение этого возрастания заключается в следующем:
Известно, что температура газа не связана колебательным движением атомов и молекул, а зависит от кинетической энергии Ek поступательного движения частиц. Но по мере роста температуры подводимая к газу теплота всё более и более перераспределяется в пользу колебательного движения, т.е. рост температуры при одинаковом подводе теплоты по мере роста температуры замедляется.
Типичная зависимость теплоемкости от температуры:
c=c0 + at
+ bt2 + dt3 + … (82)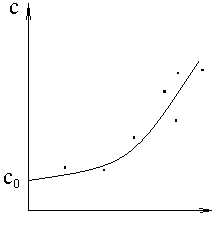
где c0, a, b, d – эмпирические коэффициенты.
c – Истинная теплоёмкость, т.е. значение теплоёмкости для заданной температуры T.
Для теплоемкости битоппроксимирующей кривой- это полином в виде ряда по степеням t.
Аппроксимирующая кривая проводится с использованием специальных методов, например, методом наименьших квадратов. Суть этого метода в том, что при его использовании все точки примерно равноудалены от аппроксимирующей кривой.
Для инженерных расчётов, как правило, ограничиваются двумя первыми слагаемыми в правой части, т.е. полагают зависимость теплоёмкости от температуры линейной c=c0 + at (83)
Средняя теплоемкость графически определяется как средняя линия заштрихованной трапеции, как известно средняя линия трапеции определяется как полусумма оснований.
Формулы применяются, если известна эмпирическая зависимость.
В тех случаях, когда зависимость теплоёмкости от температуры не удаётся удовлетворительно аппроксимировать к зависимости c=c0+at, можно воспользоваться следующей формулой:
(85)
Эта формула применяется в тех случаях, когда зависимость c от t существенно нелинейна.
Из молекулярно-кинетической теории газов известно
U = 12,56T ,U – внутренняя энергия одного киломоля идеального газа.
Ранее было получено для идеального газа:
, ,
Из полученного результата следует, что теплоемкость, полученная с использованием МКТ, от температуры не зависит.
Уравнение Майера: cp-cv=R,
cp=cv+R=12,56+8,31420,93.
Как и предыдущем случае по МКТ газов молекулярная изобарная теплоемкость от температуры не зависит.
Понятию идеального газа в наибольшей степени соответствуют одноатомные газы при малых давлениях, на практике приходится иметь дело с 2-х, 3-х … атомными газами. Например, воздух, который по объёму состоит из 79% азота (N2), 21% кислорода (O2) (в инженерных расчетах инертные газы не учитываются в силу малости их содержания) .
Можно для оценочных расчётов пользоваться следующей таблицей:
Газ | cv | cp, |
одноатомный | 12,56 | 20,93 |
двухатомный | 20,93 | 29,31 |
трехатомный | 29,31 | 37,68 |
У реальных газов, в отличие от идеального, теплоёмкости могут зависеть не только от температуры, но и от объёма и давления системы.
studfiles.net
10. Понятие теплоемкости
10.1. Общие сведения
В термодинамике теплоёмкость веществ определяется для всех агрегатных состояний: твёрдого, жидкого и газообразного. Например, у воды теплоёмкость жидкой фазы примерно в два раза больше, чем газовой – когда вода находится в виде пара.
Строго говоря, под теплоёмкостью термодинамической системы следует понимать её энергоёмкость в процессах, когда энергия к ней подводится в форме теплоты (по механизму теплообмена).
Забегая вперёд, отметим, что теплоёмкости всех веществ, значимых для техники, экспериментально определены и их значения приводятся в справочной литературе. Знание теплоёмкости вещества необходимо, главным образом для того, чтобы иметь возможность рассчитывать теплоту, которую необходимо подвести к веществу, чтобы нагреть его до определённой температуры или отвести от вещества, при его охлаждении.
Если к некоторому количеству вещества массой М, кг, подвести теплоту в количестве Q, Дж, то его температура возрастет от начальной Т1 до конечной Т2, К.
Определение:
Отношение 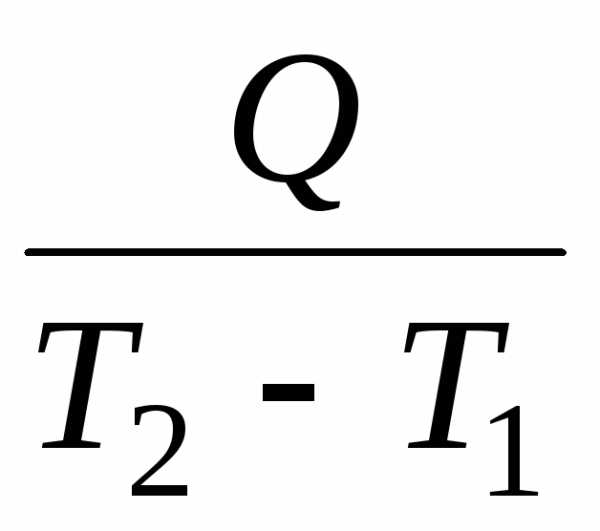 называется средней теплоёмкостьюСm в данном процессе в интервале температур
от Т1 до Т2:
называется средней теплоёмкостьюСm в данном процессе в интервале температур
от Т1 до Т2:
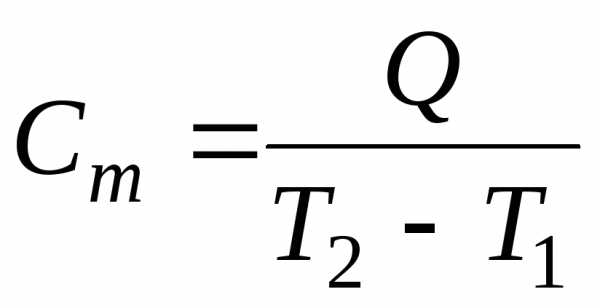 , Дж/К. (10.1)
, Дж/К. (10.1)
Из опытов известно, что в различных процессах для нагрева одного и того же вещества в одном и том же интервале температур требуются различные количества теплоты. Например, при нагреве газа при постоянном давлении теплоты потребуется больше, чем при его нагреве при постоянном объёме. Это означает, что теплоёмкость зависит от вида процесса, в котором осуществляется нагрев.
Как будет показано ниже, наибольшее практическое значение имеют теплоёмкости вещества, определяемые в двух процессах: при постоянном удельном объёме υ = const; при постоянном абсолютном давлении р = const.
Чаще всего в теплотехнических расчётах пользуются удельными массовыми теплоёмкостями.
Формула для определения средней удельной массовой теплоёмкости сm в диапазоне температур от Т1 до Т2 получается из (10.1) путём деления обоих частей равенства на массу вещества М:
,
или 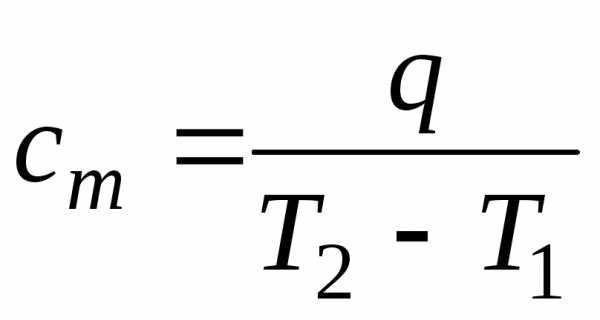 ,
Дж/(кг · К), (10.2)
,
Дж/(кг · К), (10.2)
где q – теплота, которую необходимо подвести к 1 кг вещества, чтобы изменить его температуру от Т1 до Т2, Дж/кг.
Примечание:
1) По своему физическому смыслу средняя удельная массовая теплоёмкость – это количество теплоты, которое необходимо подвести к 1 кг вещества, чтобы нагреть его на один градус.
2) Помимо удельных массовых в расчётах используются также удельные объёмные и удельные мольные теплоёмкости (подробнее об этом см. Приложение 5).
Средняя удельная теплоёмкость является свойством конкретного вещества и для данного процесса зависит только от интервала температур ΔТ = Т1 – Т2, в котором определяется.
В термодинамике, для удобства расчётов, дополнительно вводится понятие истинной удельной массовой теплоёмкости с, Дж/(кг·К).
Отличие в определении истинной теплоёмкости от средней состоит только в том, что истинная определяется по тем же соотношениям (10.1) и (10.2), но при условии, что изменение температуры вещества в ходе процесса стремится к нулю: (Т2 – Т1) = ΔТ → 0. То есть ширина интервала «стягивается» к точке Т1. Следовательно, можно сказать, что истинная теплоёмкость определяется не в интервале температур, а в точке – при одной какой-то температуре. Соответственно и зависеть она будет не от интервала температур как средняя, а просто от температуры – то есть будет является непрерывной функцией температуры, так как при разных температурах, в общем случае, значение истинной теплоёмкости будет разным.
Очевидно, что если в (10.2) знаменатель (Т2 – Т2) = ΔТ стремится к нулю, то и числитель q также будет стремиться к нулю. Из высшей математики известно, что предел такого отношения равен производной от функции q, зависящей от Т, по переменной Т:
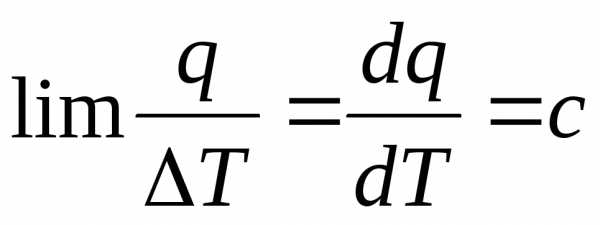 ,
Дж/(кг · К). (10.3)
,
Дж/(кг · К). (10.3)
ΔТ→0
Соотношение (10.3) можно считать определением истинной удельной массовой теплоёмкости, по которому на базе экспериментальных данных определяются её значения.
Соотношение (10.3) можно преобразовать к виду, удобному для расчёта теплоты процесса:
dq = c(T) dT. (10.4)
Если в результате процесса вещество, к примеру, нагревается от Т1 до Т2, то после интегрирования (10.4) в соответствующих пределах получим:
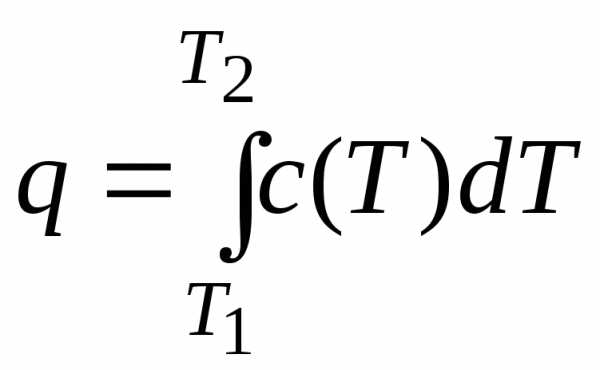 ,
(10.5)
,
(10.5)
где q – удельная теплота процесса, Дж/кг.
В термодинамике формулы (10.4) и (10.5) являются основными соотношениями для расчёта удельной теплоты в различных процессах.
Примечание:
С учётом (10.4) первый закон термодинамики (9.11) можно теперь записать в виде:
du = c(T) dT – p(υ) dυ.
Очевидно, чтобы воспользоваться соотношением (10.5) необходимо знать функцию с(Т) для данного процесса.
Следует отметить, что, благодаря экспериментам, для всех веществ удельные теплоёмкости при постоянном абсолютном давлении (в дальнейшем для краткости – при постоянном давлении) и при постоянном удельном объёме (в дальнейшем для краткости – при постоянном объёме) известны. Их значения приводятся в справочной литературе в виде таблиц. Зависимость удельной истинной теплоёмкости при постоянном давлении от температуры ср(Т) для всех технически значимых веществ в твёрдой, жидкой и газовой фазах приводится в виде стандартной формулы:
, Дж/(кг·К), (10.6)
где a1, a2 и a3 – известные коэффициенты, имеющие своё значение для каждого вещества; Т – абсолютная температура, К.
studfiles.net
6.9. Формулы и таблицы для истинных и средних теплоемкостей. Определение количества теплоты по теплоемкости и разности температур
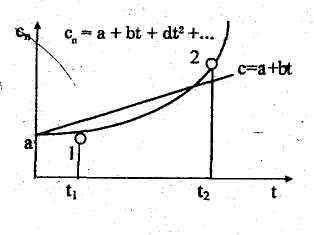 На
основании опытных данных установлено,
что зависимость
истинной теплоемкости реальных газов
от температуры является
криволинейной, как показано на рис.
6.6, и может быть выражена степенным
рядом сп=
а + bt + dt 2 +ef 3+ ….
(6.34)
На
основании опытных данных установлено,
что зависимость
истинной теплоемкости реальных газов
от температуры является
криволинейной, как показано на рис.
6.6, и может быть выражена степенным
рядом сп=
а + bt + dt 2 +ef 3+ ….
(6.34)
где а, 6, d,… постоянные коэффициенты, численные значения которых зависят от рода газа и характера протекания процесса. В тепловых расчетах часто заменяют нелинейную зависимость теплоемкости от температуры линейной.
В этом случае истинная теплоемкость определяется из
уравнения (6.35)
где t — температура, °С; b=dc/dt–угловой коэффициент наклона прямой сn = а + bt.
Исходя из (6.20), найдем формулу средней теплоемкости при ее линейном изменении от температуры согласно (6.35)
(6.36)
В случае, если процесс изменения температуры протекает в
интервале О-t , то
(6.36) принимает вид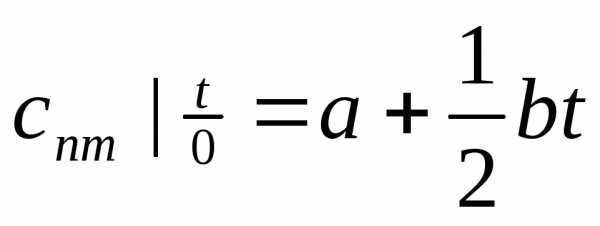 (6.37)
(6.37)
Теплоемкость 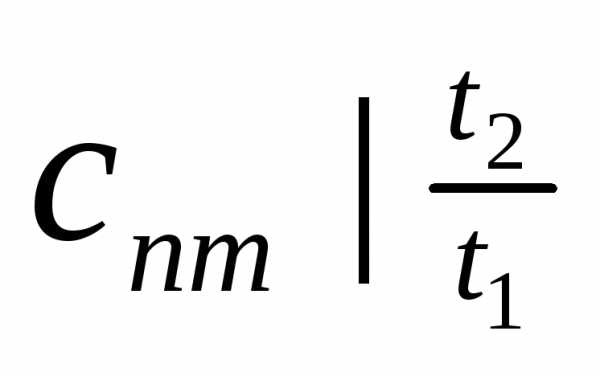 называют
теплоемкостью средней в
называют
теплоемкостью средней в
интервале температур а теплоемкость
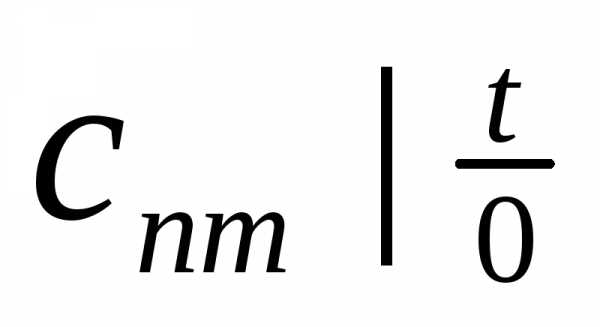 — теплоемкостью
средней в интервале 0—t.
— теплоемкостью
средней в интервале 0—t.
Результаты расчетов истинной и средней в интервале температур О—t массовой или мольной теплоемкостей при
постоянном объеме и давлении соответственно по уравнениям (6.34)и (6.37) приведены в справочной литературе. Основной тепло- и хладотехнической задачей является определение теплоты, участвующей в процессе. В соответствии с соотношением q =cndT и при нелинейной зависимости истинной теплоемкости от температуры количество теплоты определяется заштрихованной элементарной площадкой на диаграмме с координатами сnТ (рис. 6.6). При изменении температуры от Т1 до Т2 в произвольном конечном процессе количество подводимой или отводимой теплоты определяется, согласно (6.38), следующим образом:
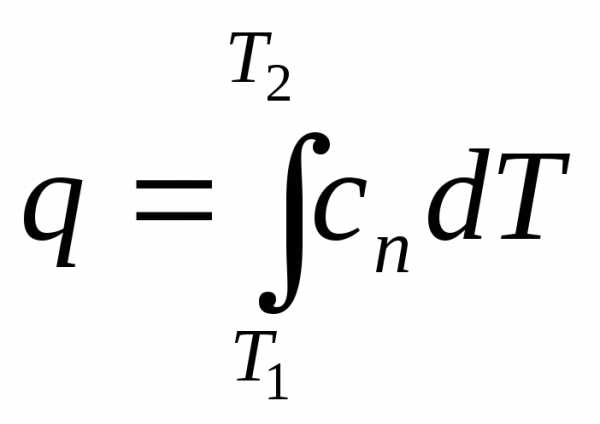 (6.38)
(6.38)
и определяется на той же диаграмме (рис. 6.6) площадью 12T2T11. Подставив в (6.38) значение сn=f(T) для данного газа по соотношению (6.34) и произведя интегрирование, получим расчетную формулу для определения теплоты в заданном интервале изменения температуры газа, которая, впрочем, следует из (6.16):
Однако, поскольку в справочной литературе есть только средняя теплоемкость в интервале температур 0—t, то количество теплоты в процессе 12 можно определить не только по предыдущей формуле, но итак: Очевидно соотношение между теплоемкостями средними в интервалах температур T1—T2 и 0-t:
Количество теплоты, подводимое (отводимое) к m кг рабо чего тела
Количество теплоты, подводимое к V м3 газа, определяется формулой
Количество теплоты, подводимое (отводимое) к н молям рабочего тела, равно
6.10Молекулярно-кинетическая теория теплоемкости
Молекулярно-кинетическая теория теплоемкости является весьма приближенной, так как не рассматривает колебательной и потенциальной составляющих внутренней энергии. Поэтому, согласно этой теории, задача состоит в определении распределения подводимой к веществу тепловой энергии между поступательной и вращательной формами внутренней кинетической энергии. Согласно распределению Максвелла-Больцмана, если системе очень_ большого числа микрочастиц сообщить некоторое количество энергии, то она распределяется
между поступательным и вращательным движением микрочастиц пропорционально их числу степеней свободы. Число степеней свободы молекулы газа (п. 5.4) соответствует числу координат, определяющих ее положение в пространстве.Молекула одноатомного газа имеет три степени, свободы, так как ее положение в пространстве определяется тремя координатами, причем для одноатомного газа эти три степени свободы являются степенями свободы поступательного движения.
Для двухатомного газа значения трех координат одного атома еще не определяют положение молекулы в пространстве, так как после определения положения одного атома необходимо учитывать, что второй атом имеет возможность вращательного движения. Для определения положения в пространстве второго атома необходимо знать две его координаты (рис. 6.7), а третья же определится из известного в аналитической геометрии уравнения
где 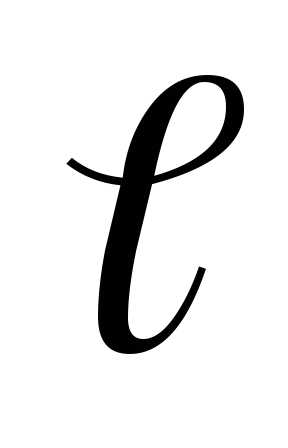 —
расстояние между атомами. Таким образом,
при известном
—
расстояние между атомами. Таким образом,
при известном 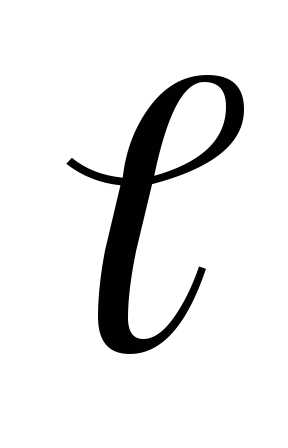 из
шести координат необходимо знать только
пять. Следовательно, молекула двухатомного
газа имеет пять степеней
свободы, из которых три — поступательного
и две — вращательного
движения.
из
шести координат необходимо знать только
пять. Следовательно, молекула двухатомного
газа имеет пять степеней
свободы, из которых три — поступательного
и две — вращательного
движения.
Молекула
трехатомного газа имеет шесть степеней
свободы
— три поступательного и три вращательного
движения. Это
следует из того, что для определения
положения в пространстве
необходимо знать шесть координат
атомов, а именно:
три координаты первого атома, две
координаты второго атома
и одну координату третьего. Тогда
положение атомов в пространстве
будет полностью определено, так как
расстояния между
ними 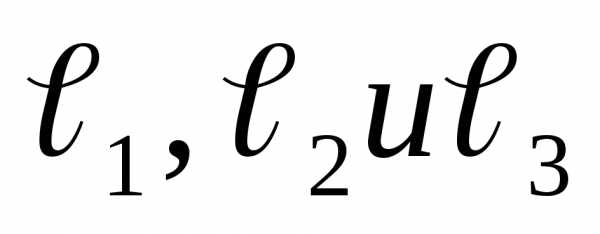 –
заданы.
–
заданы.
Если взять газ большей атомности, то есть 4-атомный и более, то число степеней свободы такого газа будет равно также шести, так как положение четвертого и каждого следующего атома будет определяться фиксированным расстоянием его от других атомов.
Согласно молекулярно-кинетической теории вещества, средняя кинетическая энергия поступательного и вращательного движений каждой из молекул пропорциональна температуре
и
равна соответственно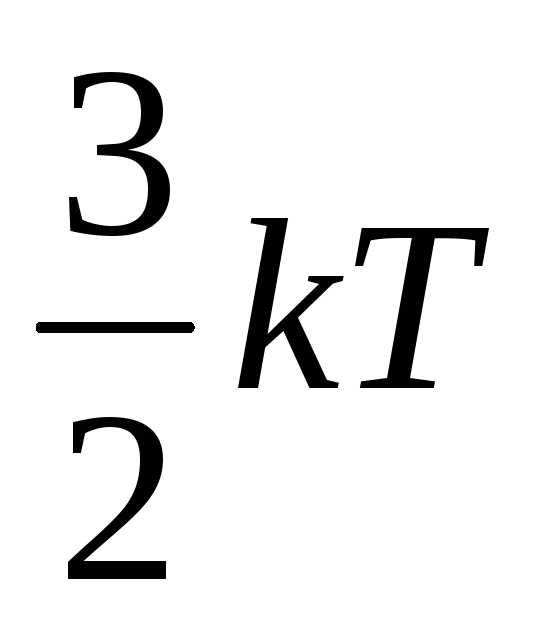 и
и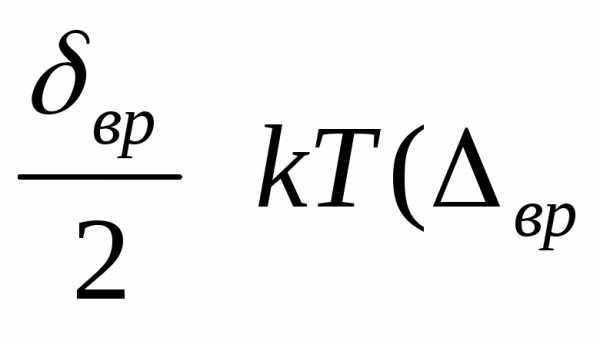 —
число степеней свободы
вращательного движения). Поэтому
кинетическая энергия
поступательного и вращательного
движений всех молекул будет
линейной функцией температуры
—
число степеней свободы
вращательного движения). Поэтому
кинетическая энергия
поступательного и вращательного
движений всех молекул будет
линейной функцией температуры
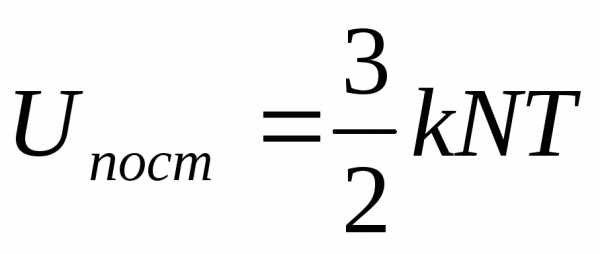 Дж, (6.39)
Дж, (6.39)
(6.40)
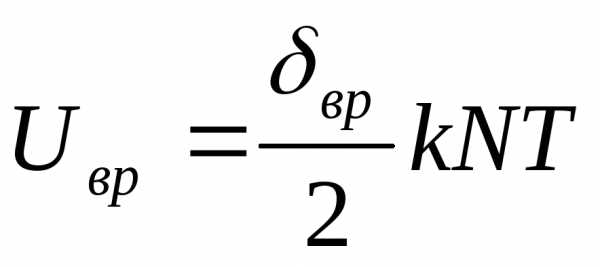 Дж.
Дж.Уравнения (6.39) и (6.40) выражают упомянутый закон равнораспределения энергии по степеням свободы, согласно которому на каждую степень свободы поступательного и вращательного движений молекул приходится одна и та же средняя кинетическая энергия, равная 1/2 (кТ).
Энергия колебательного движения молекул представляет собой сложную возрастающую функцию температуры и только в отдельных случаях при высоких температурах может быть приближенно выражена формулой, аналогичной (6.40). Молекулярно-кинетическая теория теплоемкости не учитывает колебательного движения молекул.
Между
двумя молекулами реального газа
действуют силы отталкивания
и притяжения. Для идеального газа
потенциальная
энергия взаимодействия молекул
отсутствует. С учетом изложенного
внутренняя энергия идеального газа
равна U=.Так
как N=vnNA ,то
Внутренняя энергия одного моля идеального
газа при условии, что универсальная
газовая постоянная определяется
произведением двух констант: 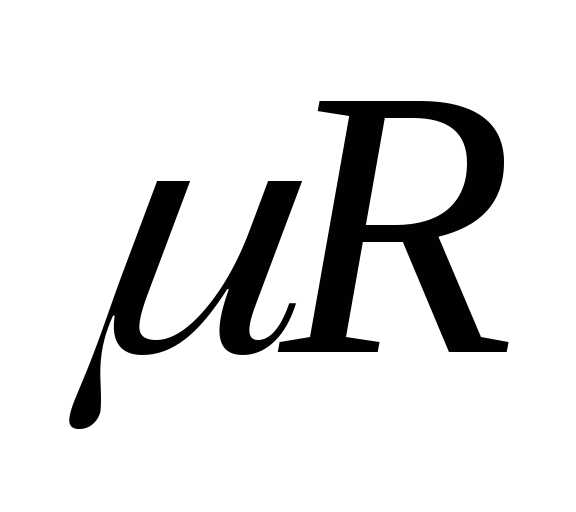 = kNA, определяется
следующим образом:,Дж/моль.
= kNA, определяется
следующим образом:,Дж/моль.
Продифференцировав
по Т и зная, что du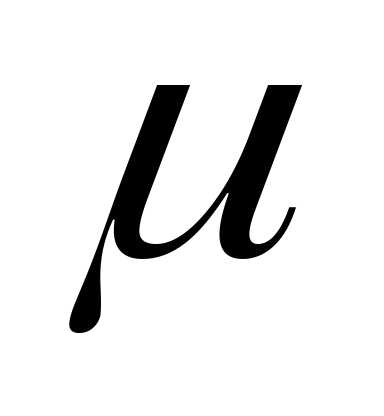 /dT =
/dT = 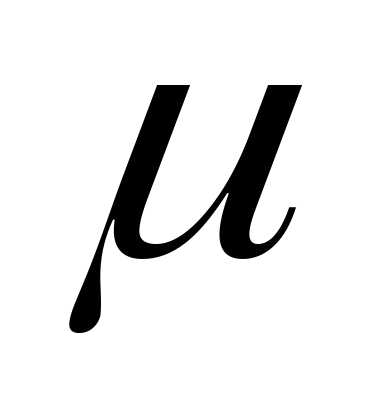 cr, получим
мольную
теплоемкость идеального газа при
постоянном объеме
cr, получим
мольную
теплоемкость идеального газа при
постоянном объеме
Коэффициент 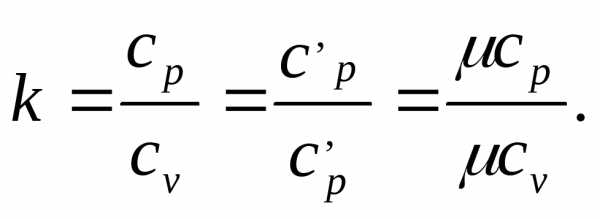 называетсякоэффициентом
Пуассона или показателем адиабаты.
называетсякоэффициентом
Пуассона или показателем адиабаты.
Для идеального газа показатель адиабаты является величиной, зависящей только от атомного строения молекул газа, что и отражено в табл. 6.1. Символическое значение показателя адиабаты можно получить из уравнения Майера сp — cv = R путем следующих преобразований: kcv — cp = R, cv(k–l) – R, откудa к = 1 + R/cv. Из предыдущего равенства следует выражение изохорной теплоемкости через показатель адиабаты cv = =R/(k—1) и затем изобарной теплоемкости: ср.= kR/(k— 1).
Из
уравнения Майера 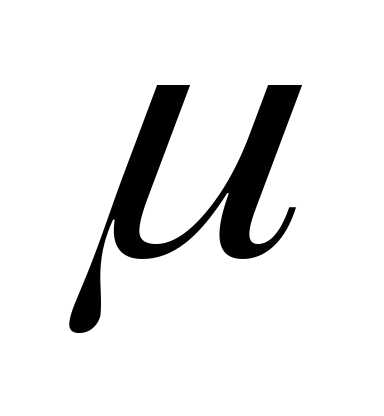 ср =
ср = 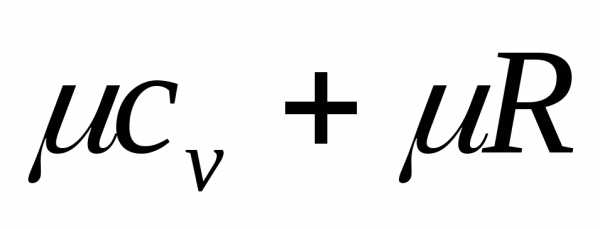 получим
выражение для мольной
теплоемкости идеального газа при
постоянном давлении
получим
выражение для мольной
теплоемкости идеального газа при
постоянном давлении 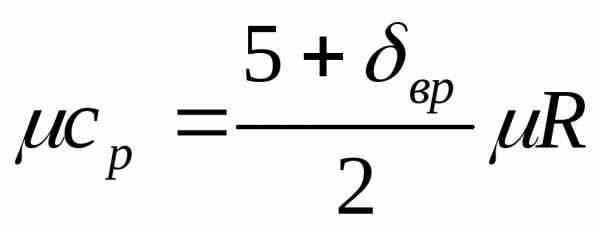 ,
Дж/(моль-К).
,
Дж/(моль-К).
Для
приближенных расчетов при не очень
высоких температурах,
когда энергию колебательного движения
атомов в молекулах
вследствие ее малости можно не учитывать,
допускаются
к использованию полученные мольные
теплоемкости 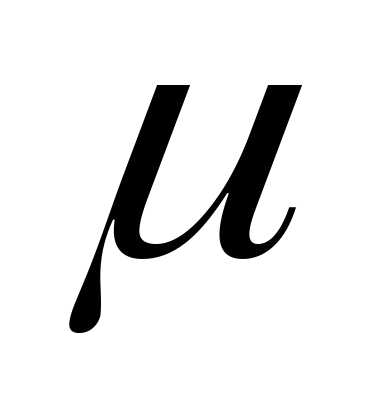 сv
сv и
и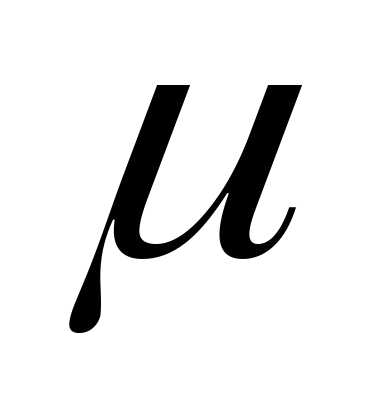 сp как
функции атомности газов. Значения
теплоемкостей
представлены в табл. 6.1.
сp как
функции атомности газов. Значения
теплоемкостей
представлены в табл. 6.1.
Таблиц6.1
Значения теплоемкостей по молекулярно-кинетической теории газов
теплоемкость Атомность газа | | | k | ||
кал | Дж | кал | Дж | ||
моль-град | моль-К | моль-град | моль-К | ||
Одноатомный газ Двухатомный газ Трех- и более атомный газ | 3 5 7 | 12,5 20,8 29,1 | 5 7 9 | 20.8 29.1 37.4 | 1,67 1,40 1,28 |
studfiles.net
Средняя теплоемкость
Часто в расчетах тепловых эффектов реакций находит применение средняя теплоемкость веществ в некотором температурном интервале Т1 – Т2, которая рассчитывается по уравнению
 =
= 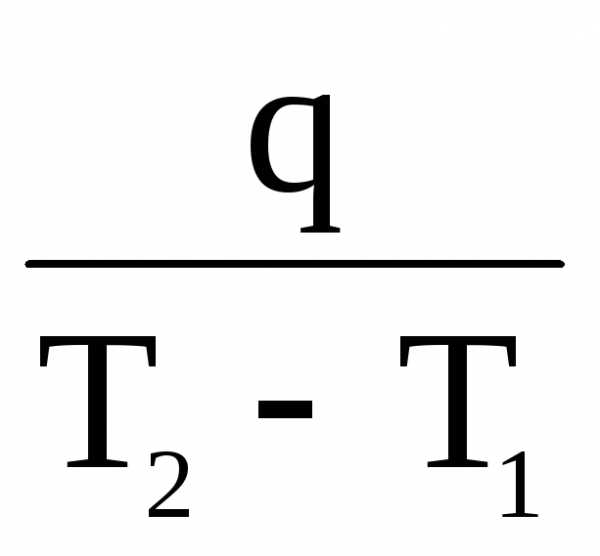 ,
,
где q – теплота, необходимая для нагревания вещества или системы в пределах от Т1 до Т2, где Т1 – Т2 – границы температурного интервала. При изменении температуры от Т1 до Т2 количество поглощенной теплоты равно
Н = 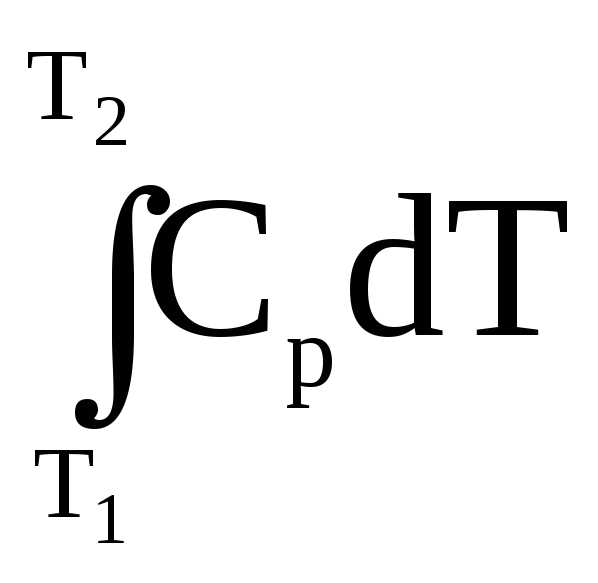 ,
,
Н = 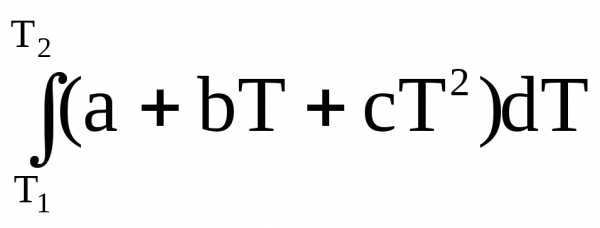 .
.
С другой стороны
q =  (T2 – T1).
(T2 – T1).
Так как q Н, приравняем правые части последних уравнений.
 (T2 – T1)
=
(T2 – T1)
= 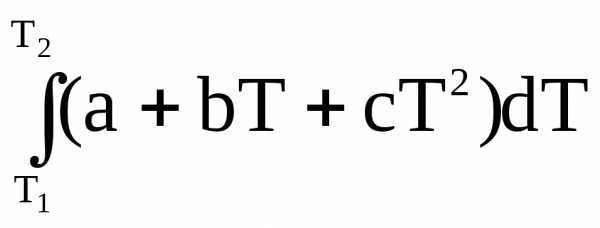
 (T2 – T1)
= а(T2 – T1)
+
(T2 – T1)
= а(T2 – T1)
+
 = а +
.
= а +
.
Если Т1 = 0, имеем
 = а +
= а + 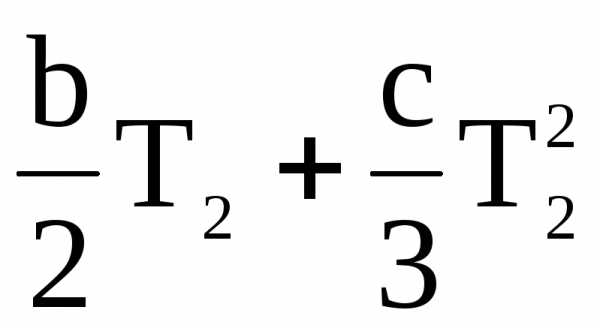 .
.
Если пренебречь третьим членом правой части (ввиду его малости), получим
 = а +
= а + 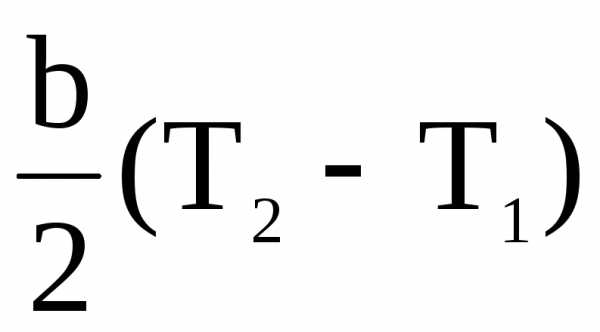 .
.
Qp Н = .
Работа тепловой машины. Теорема и цикл Карно
В эпоху начала создания паровых машин, естественно встал вопрос о коэффициенте полезного действия, как идеальной машины, так и при ее работе в реальных условиях. Такую машину в схематическом варианте можно представить состоящей из следующих частей:
1. Рабочего тела, получающего теплоту от некоторого теплового резервуара и производящего работу.
2. Самого теплоисточника как некоторого горячего резервуара с температурой Т1.
3. И холодильника или холодного резервуара, которому рабочее тело передает часть полученной им теплоты, не перешедшей в работу (в работу расширения), с температурой Т2.
Схематически представим себе процесс следующим образом.
Теплоисточник с температурой Т1 передает теплоту, количеством Q1 рабочему телу (идеальный газ). Идеальный газ частично за счет Q1 производит работу в тепловой машине А и часть теплоты, не перешедший в работу, Q2, отдает холодильнику (холодному резервуару).
В 1824 г. Сади Карно нашел способ вычисления максимальной работы, которую может совершить тепловая машина. Он впервые осознал, что отсутствует зависимость от устройства двигателя и способа, которым совершается работа, а существует лишь зависимость только от температур, обусловливающих поток теплоты. Максимальная работа достигается в тех двигателях, в которых процесс передачи теплоты происходит бесконечно медленно при бесконечно малой разности температур теплоисточника и холодильника.
Карно не получил самого выражения, позволяющего рассчитать максимальный коэффициент полезного действия тепловой машины, это сделали другие. Но он осознал и сформулировал сам принцип. Акцентируя на нем внимание читателей, отметим, что открытие С. Карно в следующем: обратимый тепловой двигатель производит максимальную работу, а максимальная величина является исключительно функцией температуры горячего и холодного резервуаров.
= А/Q1,
где А – совершенная работа, Q1 – теплота, взятая у теплоисточника.
. (25)
В последнем выражении Q1 – количество тепла, взятое у теплоисточника с температурой Т1 рабочим телом, а Q2 – количество тепла, которое не перешло в работу и передано этим телом холодильнику с температурой Т2.
Задача. Температура теплоисточника 1000 К, температура холодильника 298 К. Рабочее тело получило от теплоисточника 10000 Дж теплоты. Найти величину совершенной в равновесных условиях работы и количество теплоты, отданной холодильнику.
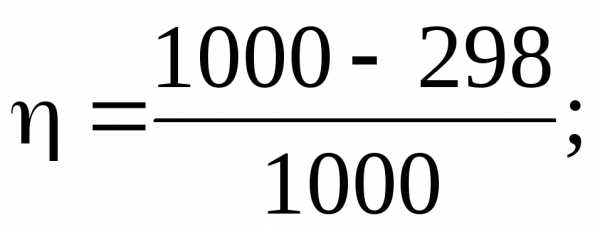
= 0,702
= 0,702
А = 0,702 Q1; A = 702 Дж; Q2 = 1000 – 702; Q2 = 298 Дж.
Обратимый цикл Карно, рассматриваемый в координатах p, V имеет вид, показанный на рис. 21.
Он состоит из четырех процессов: изотермического расширения при температуре Т1, изотермического сжатия при температуре Т2 и адиабатического расширения и сжатия газа.
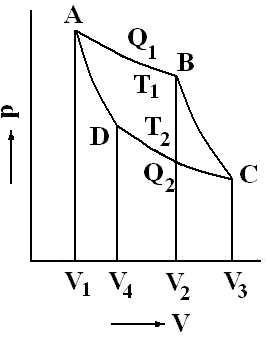
Рис. 21. Цикл Карно (проекция на координатную плоскость p – V). АВ – изотермическое расширение при температуре Т1, CD – изотермическое сжатие при температуре Т2, ВС – адиабатическое расширение и DА – адиабатическое (без подвода тепла извне) сжатие при давлении pi.
Работа изотермических процессов:
А1 = RT1ln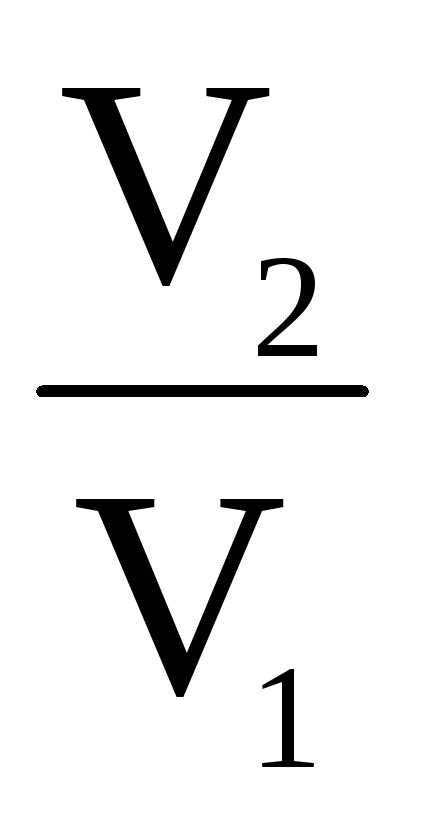 (участок
АВ)
(участок
АВ)
А3 = RT2ln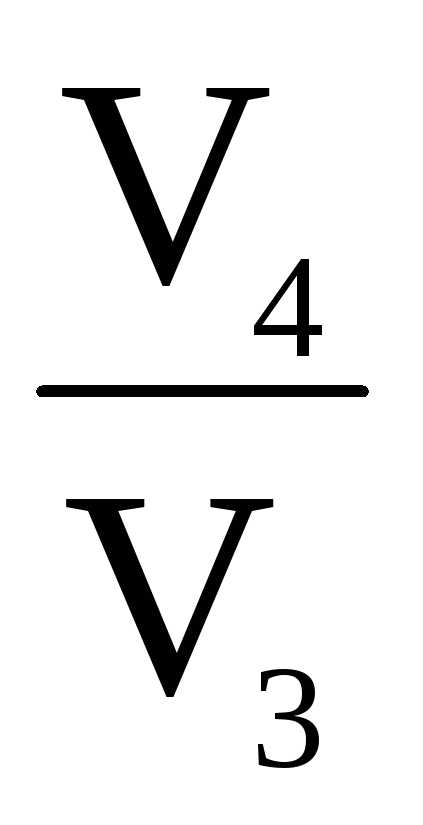 (участок
CD)
(участок
CD)
Vi – объем одного моля газа в состояниях, соответствующих точкам А, В, С и D.
Работа адиабатических процессов равна:
А2 = CV(T1 – T2) (участок ВС)
А4 = CV(T2 – T1) (участок DA).
В реальных условиях рабочий процесс тепловой машины не может происходить равновесно. Пусть для нее q1 – тепло, отданное теплоисточником тому же рабочему телу, а q – переданное последним холодильнику. Но в этих условиях q1 < Q1 q2 > Q2, следовательно
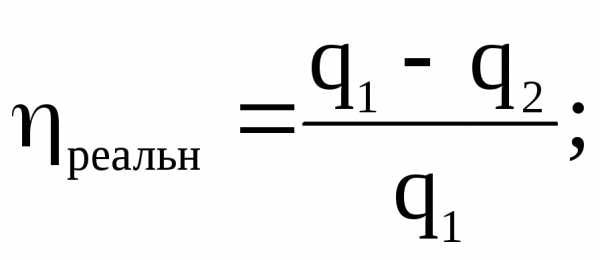
и
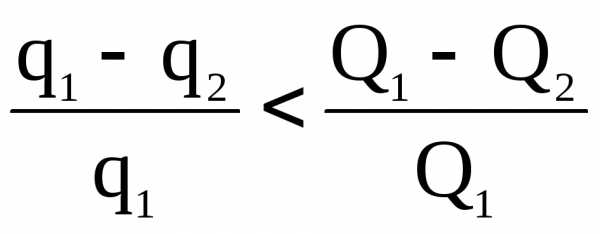 .
.
Таким образом, реальн < ид.(обратим.).
Из математического выражения (25) вытекают следующие следствия:
1. Т1 = Т2; = 0. Невозможно получить работу за счет теплоты, если имеется только один тепловой резервуар и система, совершая циклический процесс, возвращается в исходное состояние. Иначе говоря, невозможен вечный двигатель 2-го рода, когда переход теплоты в работу не сопровождается изменениями в системе.
2. Т2 = 0;
= 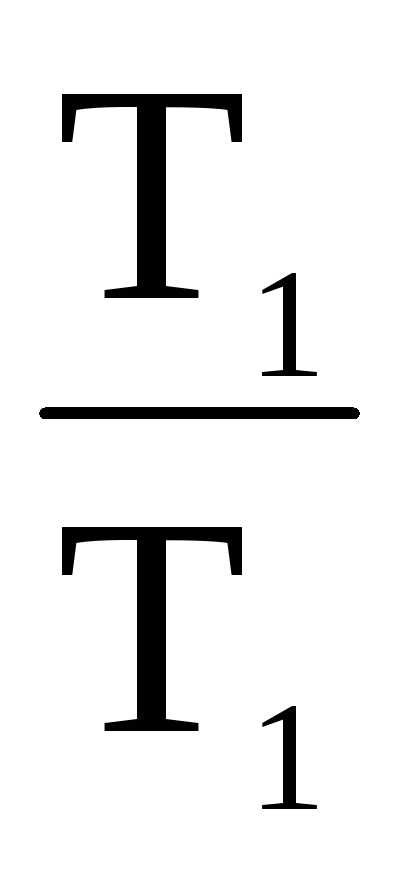 ;
= 1. Таким образом, коэффициент полезного
действия тепловой машины максимален
при любой температуре теплоисточника.
Но при этом не происходит изменений в
системе, что невозможно. Следовательно,
Т = 0 (абсолютный нуль температуры)
недостижима.
;
= 1. Таким образом, коэффициент полезного
действия тепловой машины максимален
при любой температуре теплоисточника.
Но при этом не происходит изменений в
системе, что невозможно. Следовательно,
Т = 0 (абсолютный нуль температуры)
недостижима.
studfiles.net
Истинная и средняя теплоемкости — Мегаобучалка
Теплоемкость является функцией параметров состояния – давления и температуры, поэтому в технической термодинамике различают истинную и среднюю теплоемкости.
Теплоемкость идеального газа зависит только от температуры и по определению может быть найдена лишь в интервале температур . Однако всегда можно предположить, что этот интервал очень мал вблизи какого-либо значения температуры. Тогда можно сказать, что теплоемкость определена при данной температуре. Такая теплоемкость называется истинной.
В справочной литературе зависимость истинных теплоемкостей ср и сv от температуры задают в виде таблиц и аналитических зависимостей. Аналитическую зависимость (например, для массовой теплоемкости) обычно представляют в виде полинома:
Тогда количество подведенной в процессе теплоты в интервале температур [t1,t2] определяется интегралом:
. (2)
При исследовании термодинамических процессов часто определяют среднее в интервале температур значение теплоемкости. Она представляет собой отношение количества подведенной в процессе теплоты Q12 к конечной разности температур:
. (3)
Тогда, если задана зависимость истинной теплоемкости от температуры, в соответствии с (2):
.
Часто в справочной литературе приводят значения средних теплоемкостей ср и сv для интервала температур от 0 доtоС. Как и истинные, их представляют в виде таблиц и функций:
(4)
При подстановке значения температуры t в эту формулу будет найдена средняя теплоемкость в интервале температур [0,t]. Чтобы найти среднее значение теплоемкости в произвольном интервале [t1,t2], пользуясь зависимостью (4), нужно найти количество теплоты Q12, подведенной к системе в этом интервале температур. На основании известного из математики правила интеграл в уравнении (2) может быть разбит на следующие интегралы:
.
Но
, а .
Тогда
.
После этого искомое значение средней теплоемкости находят по формуле (3).
Газовые смеси
В технике в качестве рабочих тел чаще используются не чистые вещества, а смеси различных газов. Под газовой смесью в данном случае понимают механическую смесь чистых веществ, называемых компонентами смеси, не вступающих друг с другом в химические реакции. Примером газовой смеси является воздух, основными компоненты которого являются кислород и азот. Если компонентами смеси являются идеальные газы, то и смесь в целом также будем считать идеальным газом.
При рассмотрении смесей предполагается, что:
– каждый газ, входящий в состав смеси, равномерно распределён по всему объёму, то есть его объём равен объёму всей смеси;
– каждый из компонентов смеси имеет температуру, равную температуре смеси;
– каждый газ создаёт своё давление на стенки сосуда, называемое парциальным давлением.
Парциальное давление, таким образом, это давление, которое имел бы компонент смеси, если бы он один занимал весь объем смеси при той же температуре. Сумма парциальных давлений каждого компонента равна давлению смеси (закон Дальтона):
.
Парциальным объёмом компонента V называется такой объём, который занимал бы данный компонент при давлении, равном давлению смеси, и температуре, равной температуре смеси. Очевидно, что сумма парциальных объемов равна объему смеси (закон Амага):
.
При исследовании термодинамических процессов с газовыми смесями необходимо знать ряд характеризующих их величин: газовую постоянную, молярную массу, плотность, теплоемкость и т.д. Для их нахождения должен быть задан состав смеси, определяющий количественное содержание каждого компонента, входящего в смесь. Состав газовой смеси обычно задают массовыми, объёмными или мольными долями.
Массовой долей компонента смеси g называется величина, равная отношению массы компонента к массе всей смеси:
.
Очевидно, что масса смеси m равна сумме масс всех компонентов:
,
а сумма массовых долей:
.
Объемной долей компонента смеси ri называется величина, равная отношению парциального объема компонента к объему смеси:
.
Уравнение объёмного состава смеси имеет вид:
и сумма объемных долей:
.
Мольной долей компонента смеси хiназывается величина, равная отношению числа молей этого компонента к общему числу молей смеси:
.
Очевидно, что:
.
Состав смеси задают долями единицы или в процентах. Связь между мольными и объемными долями можно установить, записывая уравнение Клапейрона – Менделеева для компонента смеси и всей смеси:
,
.
Поделив почленно первое уравнение на второе, получим:
.
Таким образом, для идеальных газов объемные и мольные доли оказываются равными.
Связь между массовыми и объёмными долями устанавливается соотношениями:
. (5)
Из закона Авогадро следует:
, (6)
где μ – молярная масса смеси, которую называют кажущейся. Она может быть найдена, в частности, через объемный состав смеси. Записывая уравнение Клапейрона – Менделеева для i-го компонента смеси в виде
и суммируя по всем компонентам, получим:
.
Сравнивая его с уравнением состояния для смеси в целом
,
приходим к очевидному соотношению:
.
Если найдена молярная масса смеси, газовая постоянная смеси может быть определена обычным способом:
. (7)
Газовую постоянную смеси можно рассчитать и через массовые доли и газовые постоянные компонентов. Запишем для каждого компонента смеси уравнение Клапейрона:
.
Суммируя по всем компонентам, получим:
.
Сумма в левой части уравнения равна объему смеси. Поделив обе части уравнения на массу смеси m
,
замечаем, что сумма в правой части уравнения представляет собой газовую постоянную смеси:
.
С учетом (6) и (7) соотношение (5) можно дополнить:
.
Используя последнее соотношение
и производя суммирование по компонентам
,
получим расчетную формулу для газовой постоянной смеси через объемные доли:
.
Удельный объем и плотность смеси и компонентов можно найти из уравнений состояния:
и ,
и .
В соответствии с определениями парциального давления и парциального объема можно записать:
.
Тогда парциальное давление компонента смеси:
.
Расчет теплоёмкости газовой смеси выполняют на основе данных о составе смеси и теплоёмкости каждого компонента. Массовая, объемная и мольная теплоемкости смеси рассчитываются через соответствующие доли:
– массовая теплоемкость
;
– объемная теплоемкость
;
– мольная теплоемкость
.
Этими формулами пользуются при определении истинных и средних теплоемкостей смеси.
megaobuchalka.ru