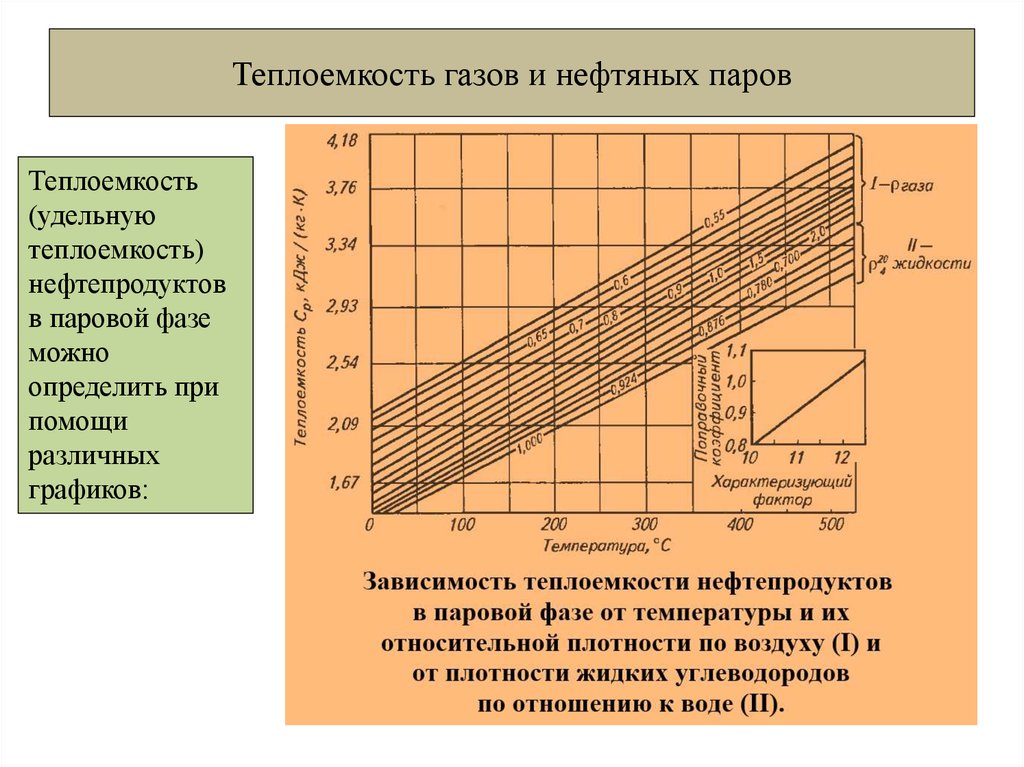
3 Теплоемкость газов
Теплоемкостью газа называют количество теплоты, необходимое для повышения его температуры на 1 К. Теплота, затраченная на повышение температуры единицы количества газа на 1 К называется удельной теплоемкостью. Принято удельную теплоемкость называть просто теплоемкостью.
В зависимости от выбранной количественной единицы различают теплоемкости: мольную Сm-кДж/(кмоль·К), массовую С – кДж/(кгК), и объемную С’ – кДж/(м3К).
Так как в 1 м3 газа могут содержаться, в зависимости от параметров его состояния, разные количества газа, принято относить 1 м3 газа к нормальным условиям (Р0= 101325 Па, Т0=273,15 К).
Между теплоемкостями существует следующее соотношение
С=; С’=; С=; С’=ρ0·С , (3.1)
где ρ
Теплоемкость газа зависит от его температуры. По этому признаку отличают истинную и среднюю теплоемкость.
Если q – удельное количество теплоты, сообщаемой единице количества вещества (или отнимаемый от него) при изменении температуры от t1 до t2 , то величина
=q/(t2– t1)=q/( Т2– Т1), (3.2)
Представляет собой среднюю теплоемкость в пределах от t2 до t1.
Предел этого отношения, когда разность температур стремиться к нулю, называют истинной теплоемкостью. Аналитически последняя определяется как
(3.3)
Теплоемкость зависит от вида процесса сообщаемая газу теплоты.
Для
теплотехнических расчетов особое
значение имеют теплоемкости газов при
постоянном давлении
и при постоянном объеме.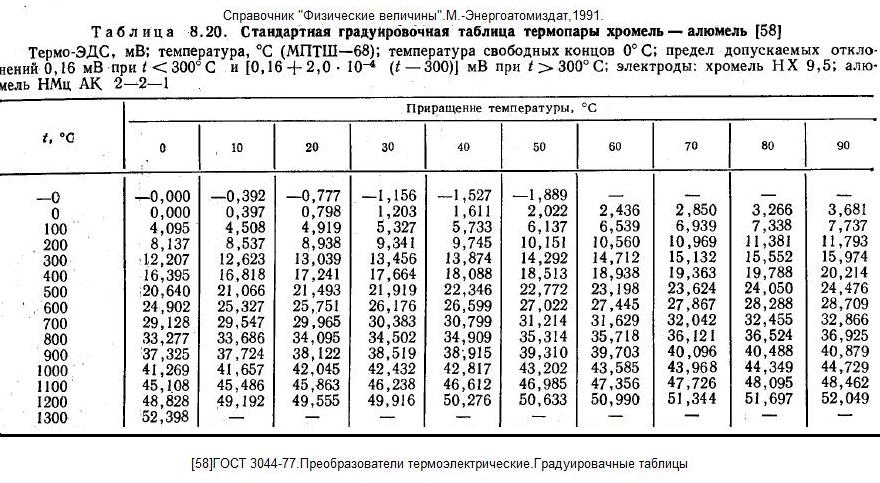
Между массовыми теплоемкостями исуществуют соотношения
(3.4)
где к– показатель адиабаты.
Постоянная теплоемкость политропного процесса с показателем n находитcя из выражения
. (3.5)
Для приближения расчетов при невысоких температурах теплоемкость можно считать постоянной.
Таблица 3.1 Приближенные значения мольных теплоемкостей при -const, р-сonst
Газы | Теплоемкость, кДж/(кмоль∙К) | Теплоемкость, КДж/(кмоль∙К) | Показатель адиабаты, К |
Одноатомные | 20,93 | 12,56 | 1,67 |
Двухатомные | 29,31 | 20,93 | 1,4 |
Трех- и многоатомные | 37,68 | 29,31 | 1,2 |
При
точных расчетах учитывают криволинейную
зависимость теплоемкости от температуры
и пользуются табличными значениями
средних теплоемкостей в интервале от
0°С до t
°С (Приложение1).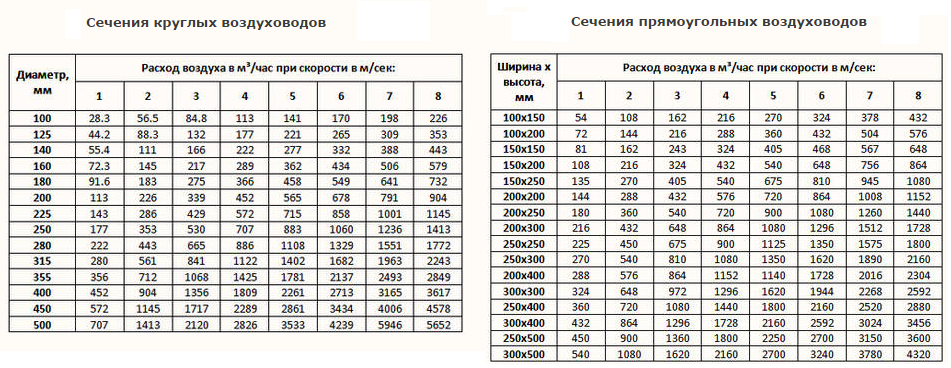 Их
отмечают сверху черточкой и указанием
границ температур. Например :
и т.д.
Их
отмечают сверху черточкой и указанием
границ температур. Например :
и т.д.
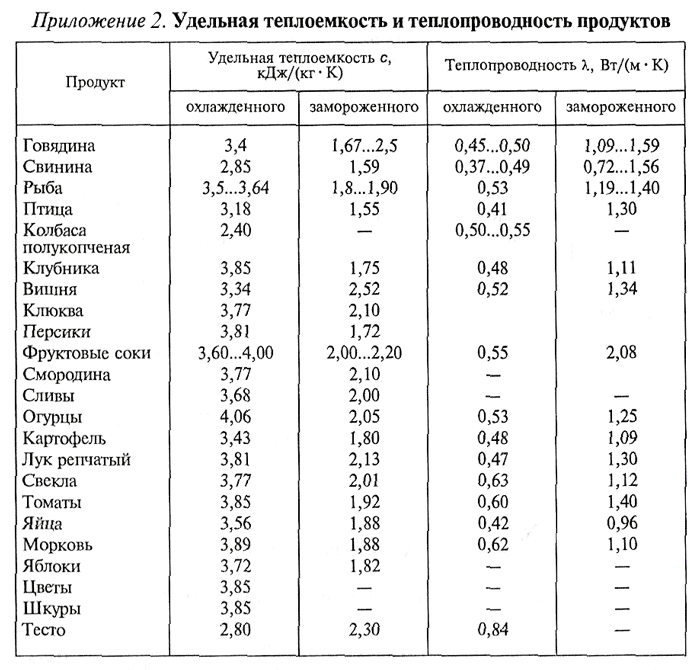
Менее точные расчеты, применяемые в технике получаются при использовании линейной зависимости теплоемкости от температуры (Приложение 2).
Средняя теплоемкость в этом случае определяется в интервале температур от t1 до t2 по уравнению
(3.6)
где a и b– величины, зависящие от физических свойств газа и постоянные для данного газа.
При пользовании таблицами значения истинных теплоемкостей, а также средних теплоемкостей в пределах от 0°С до t°С берутся непосредственно из таблиц, причем в необходимых случаях проводится интерполирование.
Количество теплоты, которое необходимо затратить для нагревания или охлаждения рабочих тел определяются из соотношений
а) для 1 кг
(3.7)
для m кг
(3.
б) для 1 нормального кубического метра газа
; (3.9)
для объема Vo в м3
(3.10)
В зависимости от условий, при которых протекают нагревание (охлаждение) газа (V- const , p- const ) в формулах 3.6…З.10 ставятся соответствующие значения теплоемкости.
Теплоемкость смеси идеальных газов
массовая ; (3.11)
объемная (3.12)
Задачи
Задача 3.1. Вычислить количество теплоты необходимой на нагревание при постоянном давлении р=100 кПа ,60 м3 воздуха от 10° до 500°С. Задачу решить в трех вариантах:
а) считая зависимость теплоемкости от температуры криволинейной;
б) пользуясь формулой линейной зависимости средней теплоемкости воздуха от температуры;
в)
полагая, что теплоемкость не зависит
от температуры.
Решение. Количество теплоты, необходимое на нагревание воздуха, исходя из криволинейной зависимости теплоемкости от температуры определяем по следующей формуле, полученной на основании уравнений (3.7)и(3.8)
.
Если использовать при решении задачи объемные теплоемкости, то нужно найти объем воздуха при нормальных условиях (Р0=101325 Па и Т0=273,15 К). Можно определить массу воздуха и применить массовые теплоемкости.
Определяем массу воздуха по уравнению
Из приложения 1 выбираем средние изобарные массовые теплоемкости от 0 до 10 и от 0 до 500°С.
В случае линейной зависимости теплоемкости от температуры формула для определения количества теплоты будет выглядеть
а при постоянной теплоемкости
Во
второй случае использовали уравнения
(3. 6), (3.8) и приложение 2, а в третьем- (3.1),
(3.8) и таблицу 3.1.
6), (3.8) и приложение 2, а в третьем- (3.1),
(3.8) и таблицу 3.1.
Задача 3.2. В котел-утилизатор поступают дымовые газы с температурой 1200°С следующего объемного состава: СО2=12%; О2=6%,N=74%; пары воды H2O=8% при давлении 200 кПа. Определить количество подаваемой теплоты нагреваемой воде, если температура газов при выходе из котла 200°С, к.п.д котла – 70% и расход дымовых газов 10 м 3/ч
Решение. Определяем количество теплоты, отведенной от дымовых газов по уравнению
где Vo – объём газовой смеси при нормальных условиях;
– объемные доли отдельных компонентов дымовых газов.
Из уравнения состояния для m кг идеального газа необходим объем дымовых газов при нормальных условиях
Среднюю теплоемкость газов, входящих в состав дымовых газов берем из приложения 1
Задача
3. 3. Вычислить количество теплоты, удаляемое
из птичника с отсасываемым воздухом,
если температура внутри помещения 16,а
наружного – 0°С. Объемная подача вентилятора
20 тыс. стандартных м3/ч.
3. Вычислить количество теплоты, удаляемое
из птичника с отсасываемым воздухом,
если температура внутри помещения 16,а
наружного – 0°С. Объемная подача вентилятора
20 тыс. стандартных м3/ч.
Задача
3.4. В конденсатор холодильной установки с
водяным охлаждением поступает газообразный
аммиак давлением р =1,05 MПa
и температурной 122°С,
охлаждается
до t=27°C.
Объемный расход аммиака V
t=0
Задача 3.5. В баллоне объемом 60л находится кислород при давлении 5 МПа и температуре 20°С. Какое количество тепла подведено, к кислороду, если его температура повысилась до 150°С. Какое давление установится при этом в сосуде? Зависимость теплоемкости от температуры. принять криволинейной.
Задача
3. 6. В воздухоподогревателе котельного
агрегата дутьевой воздух нагревается
дымовыми газами, от 20 до 200°С. При этом
температура, дымовых газов понижается
от 350 до 160°С. Объемный состав дымовых
газов: СО2=12%;
О2=6%,N=74%,
H 2O=8%.
Определить соотношение расходов воздуха
и дымовых газов. Зависимость теплоемкости
газов и воздух от температуры считать
прямолинейной.
6. В воздухоподогревателе котельного
агрегата дутьевой воздух нагревается
дымовыми газами, от 20 до 200°С. При этом
температура, дымовых газов понижается
от 350 до 160°С. Объемный состав дымовых
газов: СО2=12%;
О2=6%,N=74%,
H 2O=8%.
Определить соотношение расходов воздуха
и дымовых газов. Зависимость теплоемкости
газов и воздух от температуры считать
прямолинейной.
Задача 3.7. Определить среднюю мольную, объемную и весовую теплоемкости в процессах постоянного давления и постоянного объема в интервале температур от 0 до 1300°C для смеси газов, имеющий следующий объемный состав: 8% ; 2%и 85%; 5%.
| ГОСТы, СНиПы Карта сайта TehTab.ru Поиск по сайту TehTab.ru | Навигация по справочнику TehTab.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5
55. ОЧИСТКА ГАЗОВ ОТ ДИОКСИДА СЕРЫ
Источником
газов,
содержащих
оксиды серы, в
содовом
производстве
являются
топки печей
кальцинации
гидрокарбоната
натрия (так
называемых
огневых
кальцинаторов
или содовых
печей), а
также
топочные
газы
котельных
или ТЭЦ. SO2 может
также
содержаться
в дымовых
газах других
производств,
смежных с
содовым и
входящих с
ним в один
технологический
комплекс.
SO2 может
также
содержаться
в дымовых
газах других
производств,
смежных с
содовым и
входящих с
ним в один
технологический
комплекс.
Оксид серы образуется при сжигании топлива, содержащего серу. Большие количества серы присутствуют в жидком топливе мазуте и твердом серосодержащих углях. В газообразном топливе природном газе обычно бывает мало серы и с точки зрения борьбы с загрязнением атмосферы применение природного газа, особенно малосернистого, является лучшим решением.
Сравнивая
между собой
существующие
методы
извлечения
диоксида
серы из
дымовых
газов,
необходимо,
прежде всего,
учитывать
требования,
предъявляемые
к установкам
газоочистки,
которые, в
конечном
итоге, и
должны
определять
выбор того
или иного
решения. Эти
требования
заключаются
в следующем [94]:
Эти
требования
заключаются
в следующем [94]:
o метод очистки не должен заметно удорожать себестоимость производства основной продукции и не требовать больших площадей;
o необходимые для очистки отходящих газов реагенты не должны быть дорогими и дефицитными;
o установка для очистки газов долина быть гибкой по отношению к возможным колебаниям режимов в основном производственном процессе;
o коррозия оборудования должна быть сведена к минимуму;
o метод не должен требовать большой реконструкции существующего производственного оборудования;
o газы,
выбрасываемые
из установки,
должны
содержать
минимальное
количество
сернистого
ангидрида, а
температура
их должна
быть
достаточно
высокой,
чтобы
обеспечить
хорошее
рассеивание
в атмосфере.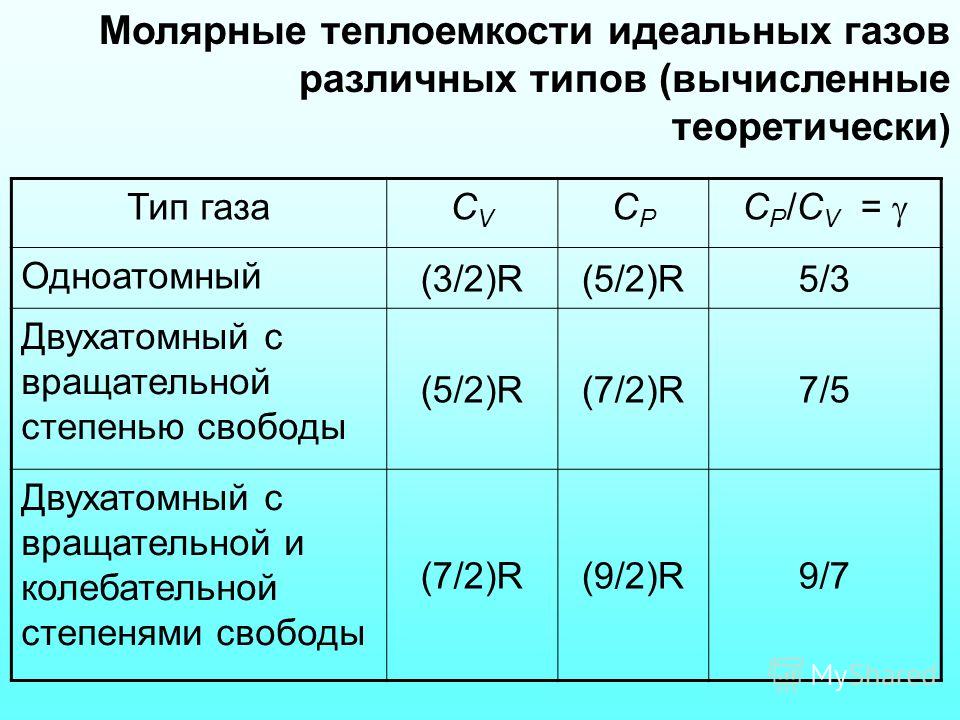
Применимость
того или
иного метода
извлечения
диоксида
серы из
отходящих
газов также
зависит от
свойств
самого газа:
температуры,
влажности и,
особенно, от
содержания SO2. Если
объемная
доля SO2
в газе
превышает 4 %,
то такой газ
может быть
переработан
на серную
кислоту
хорошо
известными
методами (см.
например [95]).
Для
переработки
более
разбавленных
газов
требуются
особые
методы.
Низкая, а
также
переменная
концентрация
сернистого
ангидрида в
отходящих
газах
является
существенным
фактором,
затрудняющим
разрешение
проблемы
очистки
таких газов.
Несмотря на
большое
число
предложенных
и
опробованных
в
производственных
условиях
методов,
задача
полного
улавливания
сернистого
ангидрида на
большинстве
заводов пока
не решена. Это
объясняется
тем, что все
существующие
методы
очистки
отходящих
газов от SO2
являются в
достаточной
мере
дорогими.
Причем
затраты
возрастают
почти
пропорционально
понижению
концентрации
SO2 в
очищенном
газе [94]. Поэтому
при выборе
того или
иного метода
очистки
необходимо
уделять
большое
внимание
экономике
методов
улавливания
и утилизации
диоксида
серы.
Это
объясняется
тем, что все
существующие
методы
очистки
отходящих
газов от SO2
являются в
достаточной
мере
дорогими.
Причем
затраты
возрастают
почти
пропорционально
понижению
концентрации
SO2 в
очищенном
газе [94]. Поэтому
при выборе
того или
иного метода
очистки
необходимо
уделять
большое
внимание
экономике
методов
улавливания
и утилизации
диоксида
серы.
В силу актуальности проблемы очистки газов от SO2 круг работ в этой области достаточно велик. Наиболее изученные и получившие широкое применение методы очистки отходящих газов от сернистого ангидрида можно подразделить на “мокрые” и “сухие”.
“Мокрые”
методы или
методы
абсорбции,
как
представляющие
наибольший
интерес для
содового
производства
будут
подробно
рассматриваться
ниже. “Сухие”
же
адсорбционные
методы
основаны на
свойствах
пористых
материалов избирательно
поглощать
определенные
компоненты
газа. В
качестве
поглотителей
чаще всего
используются
активированный
уголь и кокс.
Также широко
применяются
оксиды таких
металлов, как
Fe, Al, Co, Cu, Ti и др. В роли
поглотителей
могут
выступать
природные и
искусственные
цеолиты и
синтетические
смолы. Методы
эти в
подавляющем
большинстве
характеризуются
довольно
сложной
технологией,
включающей
предварительную
очистку от
пыли и осушку
газа.
Проблемой
также
является
необходимость
периодического
обновления
сравнительно
дорогих
поглотителей.
“Сухие”
же
адсорбционные
методы
основаны на
свойствах
пористых
материалов избирательно
поглощать
определенные
компоненты
газа. В
качестве
поглотителей
чаще всего
используются
активированный
уголь и кокс.
Также широко
применяются
оксиды таких
металлов, как
Fe, Al, Co, Cu, Ti и др. В роли
поглотителей
могут
выступать
природные и
искусственные
цеолиты и
синтетические
смолы. Методы
эти в
подавляющем
большинстве
характеризуются
довольно
сложной
технологией,
включающей
предварительную
очистку от
пыли и осушку
газа.
Проблемой
также
является
необходимость
периодического
обновления
сравнительно
дорогих
поглотителей.
К менее
распространенным
путям
снижения
выбросов
диоксида
серы можно
отнести
предварительное
удаление
серы из
энергетических
топлив, а
также
введение в
зону горения
топлива
добавок,
связывающих
серу. В этой
области
газоочистки
работают
такие
известные
фирмы, как “Вестингауз”,
Дженерал
Моторс” [96].
Это
направление
является
перспективным,
но на
сегодняшний
день, как
полагают,
экономически
неоправданными.
В этой
области
газоочистки
работают
такие
известные
фирмы, как “Вестингауз”,
Дженерал
Моторс” [96].
Это
направление
является
перспективным,
но на
сегодняшний
день, как
полагают,
экономически
неоправданными.
К экзотическим путям решения рассматриваемой задачи можно отнести попытку использовать биологические процессы. [97]. В лабораторных условиях выращены бактерии, поглощающие оксиды серы из газа. Эти работы находятся на стадии лабораторных и полупромышленных испытаний, апробированы при относительно небольших объемах газа, подлежащего очистке, и пока говорить о промышленном внедрении данного метода рано
Необходимо
отметить, что
перечисленные
выше методы
извлечения
сернистого
ангидрида из
отходящих
газов
предложены
не так давно,
поэтому опыт
создания и
эксплуатации
установок,
работающих
по ним, не
столь
обширен. Потенциальные
возможности
этих методов
недостаточно
исследованы,
и поиски
наилучших
экономических
решений для
промышленного
приложения
продолжаются.
Потенциальные
возможности
этих методов
недостаточно
исследованы,
и поиски
наилучших
экономических
решений для
промышленного
приложения
продолжаются.
Наиболее изученными и экономически оправданными на сегодняшний день признан ряд методов, входящих в группу “мокрых”. Они основаны на контакте дымовых газов с водными растворами или суспензиями веществ, химически взаимодействующих с оксидами серы либо физически абсорбирующими их.
Среди
множества
исследований,
посвященных
абсорбционной
очистке,
работы, в
которых в
качестве
абсорбентов
использовали
воду и щелочь,
представляют
интерес
больше с
точки зрения
механизма
взаимодействия
с сернистым
ангидридом.
Другие же
поглотители,
такие как
сульфит -
бисульфитные
растворы,
магниевые,
аммиачные и
известковые,
широко
применяются
в
промышленности
и интересны с
практической
точки зрения.
Рассмотрим поглощение SO2 из дымовых газов водой, тем более что сама вода является одним из наиболее дешевых и доступных абсорбентов. При растворении сернистого ангидрида в воде сначала образуется сернистая кислота, которая в водном растворе распадается на ионы. Таким образом, поглощенный диоксид серы в растворе присутствует как в неизмененном состоянии, так и в виде недиссоциированной сернистой кислоты и ионов и .
Теоретически
в
поглотительном
аппарате,
работающем
противотоком,
где свежий
газ
встречает
насыщенную
диоксидом
серы воду, а
уходящий газ
соприкасается
со свежей
водой, можно
извлечь SO2 из
любого газа
до желаемой
степени
очистки, так
как над
чистой водой
парциальное
давление
оксида серы
равно нулю.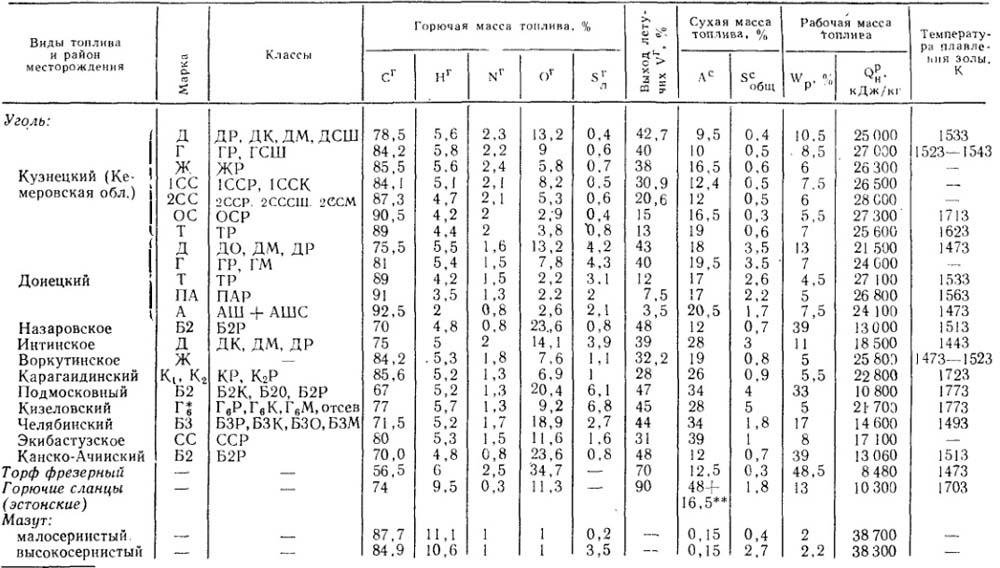 Однако
широкого
применения
водная
очистка газа
не нашла из-за
большого
потребления
воды,
обусловленного
малой
растворимостью
SO2. Известно,
что при
температуре
воды около 50 С
для промывки 1
м3 газа с
содержанием SO2
1 % требуется
около 100 л воды [95], количество
потребляемой
воды
сокращается
при более
низкой
концентрации
SO2, но
сокращение
это
незначительное.
По этим
причинам
простая
водная
промывка
применяется
редко,
когда
имеются
источники
дешевой
холодной
щелочной
воды, а также
разрешенные
для сброса
кислой воды
водоемы. Если
же условия
спуска
отсутствуют,
то сточные
воды должны
быть
нейтрализованы.
По этим
причинам
речную воду
нельзя
использовать
для мокрой
очистки
газов от SO2,
исключение
составляет
вода реки
Темза (Великобритания)
[98],
имеющая
щелочную
реакцию.
Однако
широкого
применения
водная
очистка газа
не нашла из-за
большого
потребления
воды,
обусловленного
малой
растворимостью
SO2. Известно,
что при
температуре
воды около 50 С
для промывки 1
м3 газа с
содержанием SO2
1 % требуется
около 100 л воды [95], количество
потребляемой
воды
сокращается
при более
низкой
концентрации
SO2, но
сокращение
это
незначительное.
По этим
причинам
простая
водная
промывка
применяется
редко,
когда
имеются
источники
дешевой
холодной
щелочной
воды, а также
разрешенные
для сброса
кислой воды
водоемы. Если
же условия
спуска
отсутствуют,
то сточные
воды должны
быть
нейтрализованы.
По этим
причинам
речную воду
нельзя
использовать
для мокрой
очистки
газов от SO2,
исключение
составляет
вода реки
Темза (Великобритания)
[98],
имеющая
щелочную
реакцию. Вода
реки Темза
применяется
для очистки
топочных
газов (теплоэлектростанция
в Боттэрси и
Бансайде). В
Бансайде на
практике в
воду
добавляют
меловой шлам
для
увеличения
ее
щелочности, а
к
отработанной
воде
некоторое
количество
сульфата
магния и
воздух для
окисления
сульфита в
сульфат.
Вода
реки Темза
применяется
для очистки
топочных
газов (теплоэлектростанция
в Боттэрси и
Бансайде). В
Бансайде на
практике в
воду
добавляют
меловой шлам
для
увеличения
ее
щелочности, а
к
отработанной
воде
некоторое
количество
сульфата
магния и
воздух для
окисления
сульфита в
сульфат.
К недостаткам водной промывки относят также низкую температуру газа после скруббера. В результате выходящий из дымовой трубы газ не поднимаются вверх, а рассеивается вблизи источника выброса.
Делались
попытки
использовать
в качестве
абсорбента
при очистке
газов от SO2 и
морскую воду [94]. В
литературе
указывается
на
перспективность
применения
воды в
качестве
абсорбента
для
улавливания
сернистого
ангидрида в
условиях
Крайнего
Севера.
Поскольку
сернистый
ангидрид
кислый газ,
очевидно, что
наибольший
эффект при
абсорбционном
извлечении SO2
из дымовых
газов могут
дать
абсорбенты,
имеющие
щелочной
характер.
Рассмотрим
механизм
взаимодействия
сернистого
ангидрида со
щелочью. При
промывке
газов,
содержащих SO2,водными
растворами
щелочей в
начале
процесса
диоксид серы
взаимодействует
с водой,
образуя
сернистую
кислоту,
которая
затем
частично
распадается
на ионы. Ион
водорода
связывается
присутствующей
в растворе
щелочью. Это
сдвигает
равновесие
диссоциации
сернистой
кислоты в
сторону
образования
ионов, и, в
конечном
счете,
приводит к
уменьшению
содержания в
растворе
физически
растворенного
SO2. Первоначально,
когда SO2
поступает в
избыток
щелочи,
образуется
сульфит-ион, а
при
дальнейшем
поглощении SO2
гидросульфит-ион.
Первоначально,
когда SO2
поступает в
избыток
щелочи,
образуется
сульфит-ион, а
при
дальнейшем
поглощении SO2
гидросульфит-ион.
В литературе описано достаточно много вариантов усовершенствования способа извлечения SO2 щелочью [94]. Несмотря на высокую степень очистки (до 98 %) методы этой группы, тем не менее, нельзя отнести к особо перспективным [95]. Исключение составляют случаи, когда удается преодолеть главные недостатки, характерные для этого способа, большой расход дорогостоящего поглотителя, а также его потери.
В
отличие от
воды и щелочи
растворы,
содержащие
смесь
сульфитов и
гидросульфитов
щелочных и
щелочноземельных
металлов,
нашли
относительно
широкое
распространение
в качестве
абсорбентов
для очистки
газов от SO2. Дело в том,
что в отличие
от щелочных,
сульфит
гидросульфитные
абсорбенты
можно
регенерировать
и сделать
очистку
циклической.
Во всех
методах с
использованием
таких
растворов
механизм
поглощения SO2
такой же, как
и при
использовании
щелочных
абсорбентов.
Различие
лишь в том,
что
поставщиком
ионов ОН–
является не
диссоциация
щелочи, а
гидролиз
соли
щелочного
или
щелочноземельного
металла и
слабой
сернистой
кислоты. В
результате
хемосорбционного
процесса в
абсорбенте
образуется
гидросульфит.
Если в
очищаемом
газе
присутствует
кислород, то
гидросульфит-ион
окисляется
до
нерегенерируемого
сульфата.
Последнее
нежелательно,
так как
приводит к
перерасходу
активного
компонента
раствора.
Дело в том,
что в отличие
от щелочных,
сульфит
гидросульфитные
абсорбенты
можно
регенерировать
и сделать
очистку
циклической.
Во всех
методах с
использованием
таких
растворов
механизм
поглощения SO2
такой же, как
и при
использовании
щелочных
абсорбентов.
Различие
лишь в том,
что
поставщиком
ионов ОН–
является не
диссоциация
щелочи, а
гидролиз
соли
щелочного
или
щелочноземельного
металла и
слабой
сернистой
кислоты. В
результате
хемосорбционного
процесса в
абсорбенте
образуется
гидросульфит.
Если в
очищаемом
газе
присутствует
кислород, то
гидросульфит-ион
окисляется
до
нерегенерируемого
сульфата.
Последнее
нежелательно,
так как
приводит к
перерасходу
активного
компонента
раствора.
Преимущества сульфит гидросульфитного метода: высокая степень очистки, простота и надежность работы очистных установок. К его недостаткам, как, впрочем, и любого другого мокрого, можно отнести насыщение очищенных газов водяными парами, сопровождающееся охлаждением до 40 60 оС. После сброса газа в атмосферу пар конденсируется, и термическая подъемная сила газа уменьшается. Другой недостаток получающиеся в процессе очистки продукты не всегда находят сбыт.
Широкое
применение в
промышленности
находит
магнезитовый
метод. Он
основан на
связывании
диоксида
серы оксидом
магния с
образованием
сульфита
магния.
Последний,
взаимодействуя
с сернистым
ангидридом,
может
образовать
гидросульфит. Часть
сульфита
магния под
действием
кислорода,
содержащегося
в очищаемом
газе, может
окисляться
до сульфата.
Метод
разрабатывался,
в основном, в
СНГ [99].
Отдельные
методы этой
группы
позволяют на
98 % очистить
отходящий
газ.
Часть
сульфита
магния под
действием
кислорода,
содержащегося
в очищаемом
газе, может
окисляться
до сульфата.
Метод
разрабатывался,
в основном, в
СНГ [99].
Отдельные
методы этой
группы
позволяют на
98 % очистить
отходящий
газ.
Одним из главных недостатков магнезитового метода является отложение кристаллического сульфата магния на поверхности абсорбера. Наблюдается также забивание коммуникаций кристаллами. Очистку скруббера от кристаллов сульфата магния осуществляют путем промывки теплой водой или механического удаления. В первом случае требуется установить дополнительные емкости. Второй путь трудоемок и занимает много времени.
Наличие
в цикле
получения
соды
значительных
количеств
аммиака
обуславливает
определенный
интерес к
аммиачным
методам
очистки
газов от SO2. Сущность
этих методов
заключается
в связывании
SO2 аммиаком с
получением
гидросульфита
аммония. В
промышленном
масштабе
освоен
процесс
Фулхэм-Симон-Карвез
[100].
В качестве
абсорбента
использован
аммиачный
раствор. В
выходящий из
скруббера
раствор,
содержащий
смесь NH4HSO3 и (NH4)2S2О3, добавляют 77 %-ную
серную
кислоту.
После
выдержи в
автоклаве
при давлении
1,4 МПа и
температуре
170 оСв
течение 3-х
часов
получают
элементарную
серу и
сульфат
аммония.
Сущность
этих методов
заключается
в связывании
SO2 аммиаком с
получением
гидросульфита
аммония. В
промышленном
масштабе
освоен
процесс
Фулхэм-Симон-Карвез
[100].
В качестве
абсорбента
использован
аммиачный
раствор. В
выходящий из
скруббера
раствор,
содержащий
смесь NH4HSO3 и (NH4)2S2О3, добавляют 77 %-ную
серную
кислоту.
После
выдержи в
автоклаве
при давлении
1,4 МПа и
температуре
170 оСв
течение 3-х
часов
получают
элементарную
серу и
сульфат
аммония.
Проведенные
в СНГ
усовершенствования
процесса
Фулхэм-Симон-Карвез
[101]
за счет
применения
натрийсодержащего
абсорбента
позволили
снизить
давление и
повысить
степень
очистки до 9397 %. Удалось
также
снизить
время
автоклавной
выдержки.
Удалось
также
снизить
время
автоклавной
выдержки.
В книге [94] рассмотрен
оригинальный
метод
удаления SO2
путем
распыления
аммиачной
воды в
дымовую
трубу. При
выходе из
трубы
образуется
твердая фаза
в виде
аэрозоля
сульфита
аммония,
который
окисляется
кислородом
воздуха до
сульфата
удобрения.
Эта идея
наталкивает
на мысль
ввести
сбросные
газы
основного
производства
соды,
содержащие
до 1 г/м3
аммиака, в
дымовую
трубу
теплоисточника.
Результатом
может стать
снижение
выбросов, как
аммиака, так и
кислых
компонентов
топочных
газов.
Следует
отметить, что
высокие
капитальные
и
эксплуатационные
затраты на
установки
аммиачной
очистки не
всегда
компенсируются
получаемыми
в результате
товарными
продуктами.
Для полноты освещения “мокрых” методов сероочистки стоит упомянуть менее распространенные, но также используемые в промышленных условиях абсорбенты.
Нашел применение цинковый метод, он заключается в поглощении SO2 из газов суспензией оксида цинка [97]. Известны методы с использованием в качестве абсорбента органических соединений, например, ароматических аминов, кетонов и эфиров.
По
данным [102],
в Польше на
содовом
заводе
фирмой
Bischoff (ФРГ)
установлен и
эксплуатируется
скруббер, в
котором
очистка газа
осуществляется
5 %-ным
раствором
соды. Степень
очистки
составляет 8595 %.
Здесь стоит
заметить, что
использование
дорогого
товарного
продукта
соды на
заводе, где в
избытке
имеются
пригодные
для
использования
в установке
очистки
отходы, вряд
ли можно
считать
обоснованным.
Вследствие наличия на содовых заводах больших количеств известьсодержащих отходов наибольший интерес представляют известково-известняковые способы очистки газов от SO2. Известь и, в особенности, известняк являются чрезвычайно дешевыми и доступными. Поэтому извлечение диоксида серы из газов суспензиями этих материалов широко применяется в производстве. Сущность известкового способа очистки газа от SO2 можно выразить следующими уравнениями:
Ca(OH)2+SO2=CaSO3+H2O (5.1)
CaO +
SO2 =
CaSO3
(5. 2)
2)
CaSO3 +1/2 О2 = CaSO4 (5.3)
Для поглощения SO2 можно применять известняк, и тогда уравнение реакции примет следующий вид:
CaCO3 + SO2 = CaSO3 + СO2 (5.4)
Образующиеся
по указанным
реакциям
соли
практически
нерастворимы.
К недостатку
известнякового
способа
следует
отнести
неполное
использование
CaCO3.
На
поверхности
частиц
известняка
быстро
образуется
гипсовая
корка,
которая
блокирует
дальнейшее
протекание
реакции. Надо
заметить, что
в сухом
состоянии
реакция (5. 2) идет очень
медленно. В
присутствии
воды процесс
идет быстрее,
что
указывает на
то, что
реакции (5.1)
(5.4) скорее всего
не отражают
механизма
процесса в
водной
суспензии, а
только
являются его
валовым
выражением.
2) идет очень
медленно. В
присутствии
воды процесс
идет быстрее,
что
указывает на
то, что
реакции (5.1)
(5.4) скорее всего
не отражают
механизма
процесса в
водной
суспензии, а
только
являются его
валовым
выражением.
Характерным
свойством
сернистых
солей
кальция, как,
впрочем, и
солей всех
металлов,
кроме
щелочных,
является
малая
растворимость
средних и
сравнительно
хорошая
растворимость
кислых солей [95]. В
результате
при
поглощении SО2
известью
или известняком
при
соотношении
между Са и SО2
, соответствующем
CаSО3,
получается
твердый
осадок. При
избытке же
диоксида
серы
образуется Сa(НSО3)2,
который
обладает
большей
растворимостью
и,
следовательно,
находится в
растворе.
В присутствии твердой фазы CаSО3 между концентрацией диоксида серы в газе и концентрациями Са и SО2 в растворе Сa(НSО3)2 при определенной температуре существуют вполне определенные соотношения. К сожалению, данные об этих соотношениях имеются в литературе лишь в графической форме и для расчета соответствующей аппаратуры должны быть подвергнуты математической обработке.
Простейшая
и
исторически
первая
промышленная
реализация
известнякового
способа
очистки
представляла
собой полые
скрубберы,
заполненные
кусками
известняка.
Скрубберы
орошались
водой. В
настоящее
время такие
установки
считаются
устаревшими.
Причины: затруднения
в спуске
большого
объема
сточных вод,
содержащих
гидросульфит
и сульфат
кальция, а
также
трудоемкость
операций
загрузки и
выгрузки
известняка.
Более распространен метод промывки газа суспензией извести или известняка. Процесс очистки в этом случае состоит из следующих стадий:
– очистка отходящих газов от уноса пыли и золы;
– промывка газа известковым молоком;
– отделение кристаллов сульфита и сульфата от жидкости.
При
низком
значении рН
поглотительной
суспензии в
процессе
эксплуатации
скрубберов
образуется
твердый слой
отложений
сульфата
кальция. При
высоком рН
отложения
представляют
собой мягкий
шлам. При наличии
растворенного
кислорода в
шламе
происходит
окисление
сульфита в
сульфат.
Удаление
отложений
является
одной из
главных
проблем
известнякового
и
известкового
методов. Простейшее
решение это
снижение
степени
пересыщения
раствора за
счет
обильного
орошения
скруббера.
Интенсивное
орошение
также
способствует
механическому
смыванию
кристаллов
гипса.
Простейшее
решение это
снижение
степени
пересыщения
раствора за
счет
обильного
орошения
скруббера.
Интенсивное
орошение
также
способствует
механическому
смыванию
кристаллов
гипса.
Сравнительный анализ различных абсорбентов [103], основанный на изучении результатов работы мокрых систем очистки на теплоэлектростанциях в 10 штатах США, показал следующую эффективность очистки, %:
известь 9092
зола + известь 80
известь + известняк 6099
известняк 5090
кальцинированная сода 85
Как уже
указывалось
выше, в
содовом
производстве
имеется
значительное
количество
известьсодержащих
отходов. Это,
в первую
очередь, так
называемая дистиллерная
суспензия
сток стадии
регенерации
аммиака. Он
содержит
хлориды
кальция и
натрия, а
также 4060
г/л шлама,
представляющего
собой, в
основном,
гидроксид и
карбонат
кальция, а
также
различные
силикаты, в
том числе
песок.
Естественным
представляется
использование
этого стока в
качестве
абсорбента
для очистки
газов от
кислых
компонентов
и, в частности,
от диоксида
серы.
Это,
в первую
очередь, так
называемая дистиллерная
суспензия
сток стадии
регенерации
аммиака. Он
содержит
хлориды
кальция и
натрия, а
также 4060
г/л шлама,
представляющего
собой, в
основном,
гидроксид и
карбонат
кальция, а
также
различные
силикаты, в
том числе
песок.
Естественным
представляется
использование
этого стока в
качестве
абсорбента
для очистки
газов от
кислых
компонентов
и, в частности,
от диоксида
серы.
Это тем более интересно, что, как утверждается в ряде сообщений и патентов [104, 105], хлорид кальция, содержащийся в дистиллерной суспензии, активизирует абсорбцию диоксида серы. Это обстоятельство стоит обсудить особо. Авторы выложенной заявки [106] полагают, что роль хлорида кальция заключается в связывании диоксида серы по реакции:
CaCl2 + 2
SO2 = Ca(HSO3)2 + HCl
(5. 5)
5)
Уравнение
(5.5) является
валовым и не
отражает
действительного
механизма
процесса,
однако
трудно
представить,
чтобы слабая
сернистая
кислота
вытесняла
сильную
соляную
кислоту. Тем
более что, по
мнению
авторов [106
], в
результате
реакции
образуется
не
малорастворимый
сульфит, а
относительно
хорошо
растворимый
гидросульфит
кальция. Если
активирующее
влияние
хлорида
кальция
действительно
имеет место,
что по нашему
мнению,
спорно, то оно,
скорее всего,
обусловлено
следующим
механизмом. В
результате
реакции CaCl2 и SO2
образуется
малорастворимый
сульфит
кальция. Это,
хоть и в
незначительной
степени,
сдвигает
равновесие
реакции
вправо.
Образовавшаяся
соляная
кислота
реагирует с
имеющимся в
шламе
оксидом или
карбонатом
кальция,
образуя
растворимый
хлорид
кальция. В
результате
кристаллы
сульфита
кальция
откладываются
не на
поверхности
частиц шлама,
а
кристаллизуются
в массе
раствора. Это
облегчает
растворение
твердой фазы.
В
результате
кристаллы
сульфита
кальция
откладываются
не на
поверхности
частиц шлама,
а
кристаллизуются
в массе
раствора. Это
облегчает
растворение
твердой фазы.
Вернемся к использованию отходов содового производства для очистки газов от диоксида серы. Имеются предложения по использованию для этих целей как осветленной дистиллерной суспензии, так и ее шлама. Так, в [107] в качестве абсорбента авторы применяли осветленную дистиллерную жидкость. Использование осветленной дистиллерной жидкости вряд ли оправдано из-за низкой емкости по абсорбируемым газам, и отмеченного авторами образования отложений, которые забивали опытный насадочный абсорбер.
В
выложенной
заявке [108]
предлагается
использовать
шлам
дистиллерной
суспензии
для
обработки
дымовых
газов. Набор
реагентов
для
приготовления
промывной
суспензии из
сбросов
производства
кальцинированной
соды [106]
значительно
расширен. В
частности,
предлагается
использовать
шлам,
сгущенную
суспензию
или просто
стоки
станций
дистилляции
аммиака,
очистки
рассола,
промывки
газа
известковых
печей,
водоочистки,
а также
осветленные
стоки из
установки по
обработке
промышленных
стоков.
Набор
реагентов
для
приготовления
промывной
суспензии из
сбросов
производства
кальцинированной
соды [106]
значительно
расширен. В
частности,
предлагается
использовать
шлам,
сгущенную
суспензию
или просто
стоки
станций
дистилляции
аммиака,
очистки
рассола,
промывки
газа
известковых
печей,
водоочистки,
а также
осветленные
стоки из
установки по
обработке
промышленных
стоков.
Таким образом, идея использования известьсодержащих отходов содового производства для очистки газов от оксида серы достаточно хорошо представлена в литературе. В то же время сведения о кинетике абсорбции SO2 дистиллерной суспензией в литературе отсутствуют.
При
разработке
процесса
абсорбционной
очистки
сбросных
газов
содового
производства
от диоксида
серы
исходили из
того, что в
качества
абсорбента
должна
использоваться
одна из
технологических
жидкостей. Такой подход
экономически
оправдан, так
как
позволяет
избегать
затрат на
реагенты и их
приготовление.
На первый
взгляд, выбор
подходящих
технологических
жидкостей
кажется
достаточно
большим, та
как
практически
все жидкие
среды и
суспензии в
производстве
соды имеют
щелочную
реакцию и,
следовательно,
могут быть
использованы
для
улавливания
SO2.
Однако при
более
внимательном
рассмотрении
оказывается,
что
попадание
диоксида
серы в любые
жидкости,
кроме
дистиллерной
суспензии,
приводит к
перерасходу
извести или
аммиака, так
как SO2 образует с
аммиаком
нелетучее
соединение и
на
регенерацию
аммиака из
него
необходимо
расходовать
известь.
Такой подход
экономически
оправдан, так
как
позволяет
избегать
затрат на
реагенты и их
приготовление.
На первый
взгляд, выбор
подходящих
технологических
жидкостей
кажется
достаточно
большим, та
как
практически
все жидкие
среды и
суспензии в
производстве
соды имеют
щелочную
реакцию и,
следовательно,
могут быть
использованы
для
улавливания
SO2.
Однако при
более
внимательном
рассмотрении
оказывается,
что
попадание
диоксида
серы в любые
жидкости,
кроме
дистиллерной
суспензии,
приводит к
перерасходу
извести или
аммиака, так
как SO2 образует с
аммиаком
нелетучее
соединение и
на
регенерацию
аммиака из
него
необходимо
расходовать
известь.
Таким
образом,
дистиллерная
суспензия
оказывается
единственным
абсорбентом
в технологии
производства
соды, который
может быть
использован
без
увеличения
расходов
реагентов и
энергетических
ресурсов в
нециклическом
способе
очистки
газов от
диоксида
серы. Усредненный
состав
дистиллерной
суспензии
можно
охарактеризовать
следующими
показателями:
массовая
доля в
светлой
части
дистиллерной
суспензии, %
Усредненный
состав
дистиллерной
суспензии
можно
охарактеризовать
следующими
показателями:
массовая
доля в
светлой
части
дистиллерной
суспензии, %
|
CaCl2 9,21 |
|
CaSO4 0,07 |
|
NaCl 5,42 |
|
H2O 85,14 |
|
Ca(OH)2 0,16 |
|
шлам 2,63 |
массовая доля в шламе дистиллерной суспензии, %
|
CaCO3 59,58 |
|
MgO 5,50 |
|
Ca(OH)2 17,41 |
|
SiO2 7,22 |
|
CaSO4 10,29 |
|
|
Для
применения в
промышленной
установке
очистки
газов от
диоксида
серы, так же,
как и для
установки
очистки
газов от
сероводорода,
были
рекомендованы
провальные
дырчатые
тарелки. Приведенные
ниже данные
получены на
той же
опытной
установке и
тарелке, на
которой
исследовалась
абсорбция
сероводорода.
Напомним, что
тарелка
представляла
собой диск из
нержавеющей
стали Х18Н10Т
толщиной 1 мм,
перфорированный
круглыми
отверстиями
диаметром 10
мм. Свободное
сечение
тарелки (отношение
суммарного
сечения
отверстий к
площади
тарелки)
составляло 16 %.
Приведенные
ниже данные
получены на
той же
опытной
установке и
тарелке, на
которой
исследовалась
абсорбция
сероводорода.
Напомним, что
тарелка
представляла
собой диск из
нержавеющей
стали Х18Н10Т
толщиной 1 мм,
перфорированный
круглыми
отверстиями
диаметром 10
мм. Свободное
сечение
тарелки (отношение
суммарного
сечения
отверстий к
площади
тарелки)
составляло 16 %.
Влияние
парциального
давления SO2
на скорость
абсорбции диоксида
серы
представлено
на графике
рис. 5.1. Данные
для графика
получены при
скорости
газа 1м/с,
плотности
орошения 0,002 м3/м2с, массовой
доле шлама в
суспензии 2,63 % и
температуре 22
оС. Как
видно из
этого
рисунка,
прямая
пропорциональная
зависимость
между
скоростью
абсорбции и
среднелогарифмическим
парциальным
давлением
или движущей
силой
абсорбции (далее
для
краткости
парциальным
давлением) SО2
в газовой
смеси
отсутствует. Однако на
графике
можно
выделить 2
участка. На
первом, когда
парциальное
давление не
превышает 100
Па,
пропорциональность
между
рассматриваемыми
величинами
просматривается,
и этот
участок
можно
аппроксимировать
прямой
линией (на
графике
штриховая
линия). Второй
участок
соответствует
парциальному
давлению
диоксида
серы более 100
Па.
Однако на
графике
можно
выделить 2
участка. На
первом, когда
парциальное
давление не
превышает 100
Па,
пропорциональность
между
рассматриваемыми
величинами
просматривается,
и этот
участок
можно
аппроксимировать
прямой
линией (на
графике
штриховая
линия). Второй
участок
соответствует
парциальному
давлению
диоксида
серы более 100
Па.
Этот участок
также может
быть
аппроксимирован
прямой
линией (на
рис. 5.1 штрих-пунктирная
линия), однако
она не
проходит
через начало
координат.
Такое
поведение
рассматриваемой
зависимости
свидетельствует
о том, что в
результате
увеличении
парциального
давления SO2
в газе
контроль над
скоростью
абсорбции
переходит от
одной стадии
процесса к
другой.
Для того
чтобы
разобраться
в этом,
следует
обратить
внимание на
то, что, как
показывают
простые
расчеты,
именно при
парциальном
давлении в
газе более 100 120
Па скорость
абсорбции
оказывается
выше расхода
растворенного
гидроксида
кальция,
поступающего
с орошающей
жидкостью.
При более
высоких
парциальных
давлениях
недостаток
активного
компонента
гидроксида
кальция
восполняется
за счет
растворения
этого
вещества,
содержащегося
в шламе.
Очевидно, что
взаимодействие
абсорбированного
диоксида
серы с уже
растворенным
Са(ОН)2
протекает
много
быстрее, чем
процесс
растворения
последнего
из шлама. Этим,
по-видимому, и
объясняется
изменение
наклона
кривой
зависимости
скорости
абсорбции от
парциального
давления SO2 при
значении
давления
более 100 Па.
Это предположение подтверждается данными, представленными на рис. 5.2. Из рисунка видно, что при массовой доле шлама в суспензии, не превышающей 5%, скорость абсорбции SO2 растет практически пропорционально концентрации шлама, однако при массовой доле более 5 % рост замедляется.
Рост скорости абсорбции в интервале концентраций шлама 25 % легко объяснить увеличением площади поверхности частиц извести и увеличением скорости их растворения, а снижение этого роста при концентрациях более 5 % тем, что скорость растворения становится сопоставима со скоростью транспорта диоксида серы через газовую пленку и ее растворения в жидкости.
Таким
образом,
опыты с
повышенной
концентрацией
шлама в
дистиллерной
суспензии
подтверждают,
что
лимитирующей
стадией
процесса
абсорбции
диоксида
серы
дистиллерной
суспензией
при высоких
концентрациях
SO2
является
скорость
растворения
извести.
Влияние
скорости
газа и
плотности
орошения на
кинетику
абсорбции
диоксида
серы
представлено
на рис. 5.3.
Температура
дистиллерной
суспензии 20 оС,
концентрация
в ней шлама 2,63 %.
При малых
парциальных
давлениях
диоксида
серы в газе и
соответственно
малых
скоростях
абсорбции
коэффициент
массопередачи
растет с
увеличением
скорости
быстрее, чем
при высоких
парциальных
давлениях SO2.
Такое
поведение
зависимости
коэффициента
массопередачи
от скорости, с
одной
стороны,
подтверждает
высказанное
выше
положение о
том, что
лимитирующей
стадией
процесса при
больших
скоростях
абсорбции
является
скорость
растворения
гидроксида
кальция; с
другой
стороны,
позволяет
предположить,
что при малых
скоростях
абсорбции
лимитирующей
стадией
является
массоотдача
в газовой
пленке.
Для того чтобы убедиться в этом, была выполнена математическая обработка результатов эксперимента в виде следующего уравнения.
К = a w b Lc, (5.6)
где w скорость газа в полном сечении контактного устройства, м/с; L плотность орошения, м3/м2.с; а, b и с коэффициенты.
Результаты
обработки
представлены
в табл. 5.1. Из
данных
таблицы 5.1
видно, что при
низких
парциальных
давлениях
диоксида
серы в газе
коэффициент
массопередачи
пропорционален
скорости
газа в
степени 1,62, а
влияние
плотности
орошения
незначительно.
Это
указывает на
то, что
кинетику
массопередачи
в этом
концентрационном
диапазоне
определяет
сопротивление
в газовой
пленке. Подтверждением
тому
является
также
близость
значений
коэффициентов
уравнения (4.19)
для
абсорбции
сероводорода
содо-аммиачным
раствором (см.
табл. 4.1.) и
диоксида
серы
дистиллерной
суспензией.
Подтверждением
тому
является
также
близость
значений
коэффициентов
уравнения (4.19)
для
абсорбции
сероводорода
содо-аммиачным
раствором (см.
табл. 4.1.) и
диоксида
серы
дистиллерной
суспензией.
Таблица 5.1 Значения коэффициентов уравнения (5.6) при различных парциальных давлениях ( ) SO2 в газе
|
Парциальное
давление SO2, |
Значение коэффициентов уравнения (5.1) |
F- критерий |
СКО, |
||
|
а. |
b |
с |
|||
|
250 < < 270 |
36,4 |
1,07 |
0,44 |
37 |
14 |
|
90 < < 102 |
3,89 |
1,62 |
0 |
205 |
11 |
Влияние
температуры на
кинетику
абсорбции SO2
незначительно. Значения
коэффициента
массопередачи
колеблются в
пределах
ошибки
эксперимента,
и выраженной
тенденции
его
изменения с
температурой
нет.
Отсутствие
корреляции
между
температурой
и
коэффициентом
массопередачи
подтверждает
и
математическая
обработка
результатов
эксперимента.
Таким
образом,
можно
утверждать,
что в
рассмотренном
диапазоне
температура
не оказывает
влияния на
коэффициент
массопередачи
при
абсорбции
диоксида
серы
дистиллерной
суспензией, а
следовательно,
кинетика
процесса
определяется
диффузионными
стадиями.
Значения
коэффициента
массопередачи
колеблются в
пределах
ошибки
эксперимента,
и выраженной
тенденции
его
изменения с
температурой
нет.
Отсутствие
корреляции
между
температурой
и
коэффициентом
массопередачи
подтверждает
и
математическая
обработка
результатов
эксперимента.
Таким
образом,
можно
утверждать,
что в
рассмотренном
диапазоне
температура
не оказывает
влияния на
коэффициент
массопередачи
при
абсорбции
диоксида
серы
дистиллерной
суспензией, а
следовательно,
кинетика
процесса
определяется
диффузионными
стадиями.
Как уже
указывалось,
газы,
загрязненные
диоксидом
серы, как
правило,
являются
продуктами
сгорания
органического
топлива и
содержат
значительное
количество
диоксида
углерода,
который так
же, как SO2
,
абсорбируется
дистиллерной
суспензией. Поэтому при
проектировании
установок
очистки
газов важно
знать кинетику
абсорбции СО2
и ее влияние
на
улавливание SO2.
Поэтому при
проектировании
установок
очистки
газов важно
знать кинетику
абсорбции СО2
и ее влияние
на
улавливание SO2.
Абсорбция
СО2, во
всяком
случае,
снижает
абсорбционную
емкость
поглотителя.
Впрочем,
последнее в
рассматриваемом
процессе не
является
проблемой,
так как, во-первых,
на содовых
заводах
всегда
имеется
избыток
дистиллерной
суспензии по
сравнению с
потребностью
для целей
очистки
газов; во-вторых,
технология
последующей
утилизации
дистиллерной
суспензии
предусматривает
стадию
карбонизации.
Таким
образом, в
данном
случае
абсорбцию
диоксида
углерода из
топочных
газов можно
рассматривать
как
положительный
процесс. Тем
не менее, его
особенности
должны быть
известны
проектировщику.
В табл. 5.2. приведены данные о влиянии концентрации диоксида углерода в газе на коэффициент массопередачи диоксида серы. Данные получены при следующих условиях: скорость газа 1 м/с; плотность орошения 0,002 м3/м2с; температура 60 оС
Таблица 5.2 Влияние абсорбции СО2 на кинетику абсорбции диоксида серы
|
Парциальные давления, кПа |
Коэффициент
массопередачи
по SO2, |
Скорость
абсорбции
СО2, |
Коэффициент
массопередачи
по CO2, |
|
|
СО2 |
SO2 |
|||
|
5,23 |
0,25 |
2,61 |
6,65 |
1,28 |
|
8,13 |
0,26 |
2,28 |
6,57 |
0,91 |
|
10,2 |
0,26 |
2,42 |
13,4 |
1,32 |
|
12,3 |
0,25 |
2,38 |
14,6 |
1,22 |
|
15,1 |
0,25 |
2,55 |
17,3 |
1,14 |
Как видно из
этой таблицы,
абсорбция CO2
не оказывает
влияния на
абсорбцию SO2. Это не
удивительно,
так как
угольная
кислота
значительно
слабее
сернистой и,
следовательно,
это вещество
не может
конкурировать
с диоксидом
серы в
реакции с
активным
компонентом
гидроксид
ионом. Из табл.
5.2 также
вытекает, что
скорость
абсорбции СО2
с точностью
до ошибки
эксперимента
пропорциональна
парциальному
давлению
этого
компонента в
газе.
Следовательно,
интенсивность
абсорбции
диоксида
углерода
можно
характеризовать
коэффициентом
массопередачи.
Это не
удивительно,
так как
угольная
кислота
значительно
слабее
сернистой и,
следовательно,
это вещество
не может
конкурировать
с диоксидом
серы в
реакции с
активным
компонентом
гидроксид
ионом. Из табл.
5.2 также
вытекает, что
скорость
абсорбции СО2
с точностью
до ошибки
эксперимента
пропорциональна
парциальному
давлению
этого
компонента в
газе.
Следовательно,
интенсивность
абсорбции
диоксида
углерода
можно
характеризовать
коэффициентом
массопередачи.
Влияние
скорости
газа,
плотности
орошения,
парциального
давления SO2
в газе и
температуры
на
коэффициент
массопередачи
по СО2
отражено в
табл. 5.3. В
таблице 5.4
приведены
результаты
расчета
коэффициентов
линейной
регрессии,
отражающей
зависимость
коэффициента
массопередачи
по СО2 (
) от различных
факторов.
Таблица 5.3 Влияние скорости газа, плотности орошения парциального давления SO2 в газе и температуры на коэффициент массопередачи по СО2
|
w, м/с |
L103, м3/м2с |
, Па |
t, оС |
106
, |
|
1,7 |
2,7 |
320 |
80 |
1,73 |
|
1,7 |
2,7 |
100 |
20 |
2,52 |
|
1,7 |
0,5 |
320 |
20 |
1,56 |
|
1,7 |
0,5 |
100 |
80 |
2,47 |
|
0,5 |
0,5 |
320 |
80 |
0,83 |
|
0,5 |
0,5 |
100 |
20 |
1,08 |
|
0,5 |
2,7 |
320 |
20 |
0,62 |
|
0,5 |
2,7 |
100 |
80 |
1,12 |
Таблица 5. 4
Коэффициенты
регрессии
4
Коэффициенты
регрессии
|
Переменная |
Коэффициент линейной регрессии |
Стандартная ошибка коэффициента |
Уровень значимости, % |
|
|
0,928 |
0,268 |
95,0 |
|
w |
0,964 |
0,124 |
99,5 |
|
L103 |
0,00568 |
0,0679 |
6,2 |
|
|
-0,00278 |
0,000679 |
97,4 |
|
t |
0,00154 |
0,00249 |
42,0 |
Как
видно из этих
таблиц,
значимое
влияние (на
уровне 95 %) на
коэффициент
массопередачи
по диоксиду
углерода
оказывают
только
скорость
газа и
парциальное
давление
диоксида
серы. Экспериментальные
данные по
влиянию этих
факторов на
коэффициент
массопередачи
по СО2 были
обработаны
методами
нелинейного
оценивания. В
результате
получено
следующее
уравнение:
Экспериментальные
данные по
влиянию этих
факторов на
коэффициент
массопередачи
по СО2 были
обработаны
методами
нелинейного
оценивания. В
результате
получено
следующее
уравнение:
, (5.7)
где
коэффициент
массопередачи,
моль/сПам2;
w
скорость
газа в полном
сечении
аппарата, м/с;
парциальное
давление
диоксида
серы, Па;
= 1,2110-6
моль/сПам2;
w0 =
1,0 м/с; = 260 Па;
а1 = 0,686; а2 = – 0,379.
Остаточная
среднеквадратическая
ошибка
уравнения 13 %,
коэффициент
корреляции
между
расчетом и
фактическим
значением
равен 0,98.
Влияние концентрации диоксида серы в газе на кинетику абсорбции диоксида углерода может быть обусловлено тем, что в диффузионной пленке жидкости основное количество гидроксида кальция расходуется на реакцию с SO2 ангидридом более сильной кислоты, и молекулы диоксида углерода должны проходить более длинный путь в пленке, прежде чем прореагируют с ионом кальция.
Выше
было
показано, что
скорость
абсорбции
диоксида
серы
определяется
скоростью
растворения
кальциевых
соединений,
находящихся
в шламе
дистиллерной
суспензии.
Последняя
зависит как
от
количества
ранее
поглощенного
диоксида
серы, так и от
рН, при
котором
протекает
абсорбция.
Существенным
фактором для
проектирования
газоочистной
установки,
кроме
скорости
абсорбции,
является
также
количество
диоксида
серы, которое
может быть
поглощено
дистиллерной
суспензией
до
равновесия с
очищаемым
газом, иначе
говоря
емкость
дистиллерной
суспензии. Изучены
дистиллерные
суспензии
Славянского
содового
завода и
Стерлитамакского
ОАО “Сода”,
использующих
для
получения
извести
первый мел,
второй
известняк.
Изучены
дистиллерные
суспензии
Славянского
содового
завода и
Стерлитамакского
ОАО “Сода”,
использующих
для
получения
извести
первый мел,
второй
известняк.
На рис. 5.4. представлена кривая титрования 1 дм3 дистиллерной суспензии Славянского содового завода, а на рис. 5.5 Стерлитамакского ОАО Сода.
Как
видно из
рисунков,
общий ход
кривых
титрования в
целом
совпадает.
Имеются две ступеньки
при рН 1011
и 45,
обусловленные
титрованием
гидроксида и
карбоната
кальция
соответственно.
Основные
отличия
рассматриваемых
кривых
заключаются
в наклоне
площадки,
соответствующей
титрованию
гидроида
кальция (на
рис. 5. 4 наклон
больше) и
форме кривой
на переходе
между
площадками,
соответствующими
гидроксиду и
карбонату
кальция. На
рис. 5.4 этот
участок
более
пологий,
кроме того, на
рис. 5.5 имеется
выраженная,
хотя и
небольшая “ступенька”
при рН = 8,5,
которая
соответствует
титрованию
индивидуального
вещества,
возможно,
оксида
магния.
4 наклон
больше) и
форме кривой
на переходе
между
площадками,
соответствующими
гидроксиду и
карбонату
кальция. На
рис. 5.4 этот
участок
более
пологий,
кроме того, на
рис. 5.5 имеется
выраженная,
хотя и
небольшая “ступенька”
при рН = 8,5,
которая
соответствует
титрованию
индивидуального
вещества,
возможно,
оксида
магния.
Указанные отличия кривых обусловлены тем, что в шламе дистиллерной суспензии Славянского содового завода находится значительно больше трудно гидратируемых кальциевых соединений, чем в суспензии Ст. ОАО “Сода”. Иными словами, кривые титрования свидетельствуют о более высоком качестве извести, получаемой из известняка.
Массовая
доля
диоксида
серы в
выбрасываемом
после
очистки газе
обычно
нормируется
на основании
расчетов
рассеивания
в
зависимости
от ряда
параметров. Как правило,
она
составляет 1,10-3
3,10-3 %.
Обработка
экспериментальных
данных, по
определению,
установившегося
(равновесного)
значения
величины рН
воды, сквозь
которую
предварительно
пропускали
воздух,
содержащий
диоксид серы,
дает
следующее
уравнение
для расчета
величины рН:
Как правило,
она
составляет 1,10-3
3,10-3 %.
Обработка
экспериментальных
данных, по
определению,
установившегося
(равновесного)
значения
величины рН
воды, сквозь
которую
предварительно
пропускали
воздух,
содержащий
диоксид серы,
дает
следующее
уравнение
для расчета
величины рН:
pH = 2,23 0,633lg C, (5.8)
где С массовая доля диоксида серы в газовой смеси, %.
С
помощью
расчетов по
уравнению (5.8)
находим, что
указанным
выше
нормативным
концентрациям
диоксида
серы в газе
соответствует
рН
абсорбента 3,8
4,1. Очевидно,
что это то
предельное
значение, до
которого
может
снизиться рН
дистиллерной
суспензии в
процессе
взаимодействия
с газом,
содержащим SO2. По графикам
рис. 5.4, 5.5
получаем, что
снижение рН
дистиллерной
суспензии до
4-х происходит
при
добавлении 0,36
моль НСl на 1
дм3
дистиллерной
суспензии
Славянского
содового
завода и 0,42
моль НСl
на 1 дм3
дистиллерной
суспензии Ст.
ОАО Сода. Эти
количества соляной
кислоты
эквивалентны
0,18 и 0,21 моль (или
11,5 и 13,4 г) SO2
соответственно.
Это и есть
максимальная
емкость
рассмотренных
дистиллерных
суспензий по
диоксиду
серы.
По графикам
рис. 5.4, 5.5
получаем, что
снижение рН
дистиллерной
суспензии до
4-х происходит
при
добавлении 0,36
моль НСl на 1
дм3
дистиллерной
суспензии
Славянского
содового
завода и 0,42
моль НСl
на 1 дм3
дистиллерной
суспензии Ст.
ОАО Сода. Эти
количества соляной
кислоты
эквивалентны
0,18 и 0,21 моль (или
11,5 и 13,4 г) SO2
соответственно.
Это и есть
максимальная
емкость
рассмотренных
дистиллерных
суспензий по
диоксиду
серы.
В
реальных
условиях
работы
газоочистной
установки,
когда время
контакта
газа с
дистиллерной
суспензией
ограничено,
скорость
растворения
шлама может
оказаться
недостаточной
и тогда не вся
емкость
может быть
использована.
Данные по скорости
растворения
твердой фазы
дистиллерной
суспензии
при
температуре 800,5
оС
представлены
на рис. 5.6 для
Славянского
содового
завода и на
рис. 5.7 для Ст.
ОАО Сода.
Характер
кинетических
кривых для
обоих
заводов
практически
одинаков.
5.6 для
Славянского
содового
завода и на
рис. 5.7 для Ст.
ОАО Сода.
Характер
кинетических
кривых для
обоих
заводов
практически
одинаков.
Имеется
область
больших
скоростей
растворения ( I ),
которая
ограничена
первыми 12
мин и область
малых
скоростей ( II ).
Интересно,
что скорость
растворения
шлама в этой
последней
области
связана с
наклоном
кривой
титрования.
Так, на рис. 5.4
крутизна
кривой
титрования
при рН 6 и 8
примерно
одинакова и
соответственно
одинаковы
скорости
растворения
в области
малых
скоростей
при этих
значения рН.
На рис. 5.5
кривая
титрования
при рН 8
проходит
круче, чем при
рН 6.
Соответственно
разные и
скорости
растворения,
причем если
крутизна
кривой
титрования
больше, то
скорость
растворения
в области
малых
скоростей
меньше. В этом
легко
убедиться,
сопоставив
кинетические
кривые при рН
6 и 4 и
соответствующие
отрезки
кривой
титрования.
Такой
результат
объясняется
тем, что
крутизна
кривой
титрования
определяет
количество
вещества,
переходящее
в раствор при
изменении рН
на единицу.
Чем меньше
наклон, тем
больше
растворяется
шлама,
следовательно,
круче
кинетическая
кривая.
В этом
легко
убедиться,
сопоставив
кинетические
кривые при рН
6 и 4 и
соответствующие
отрезки
кривой
титрования.
Такой
результат
объясняется
тем, что
крутизна
кривой
титрования
определяет
количество
вещества,
переходящее
в раствор при
изменении рН
на единицу.
Чем меньше
наклон, тем
больше
растворяется
шлама,
следовательно,
круче
кинетическая
кривая.
Следует
отметить, что
в процессе
очистки газа
от кислых
компонентов
реально
может быть
использована
только та
часть шлама
дистиллерной
суспензии,
которая
успевает
раствориться
за 12 мин.
Обычно
полагают, что
на
поверхности
раздела фаз
газ-жидкость
устанавливается
равновесие.
Поскольку
самой
медленной
стадией при
поглощении
диоксида
серы
дистиллерной
суспензией
является
растворение
шлама, то такое
равновесие
будет
существовать
и между всем
объемом газовой
и жидкой фаз.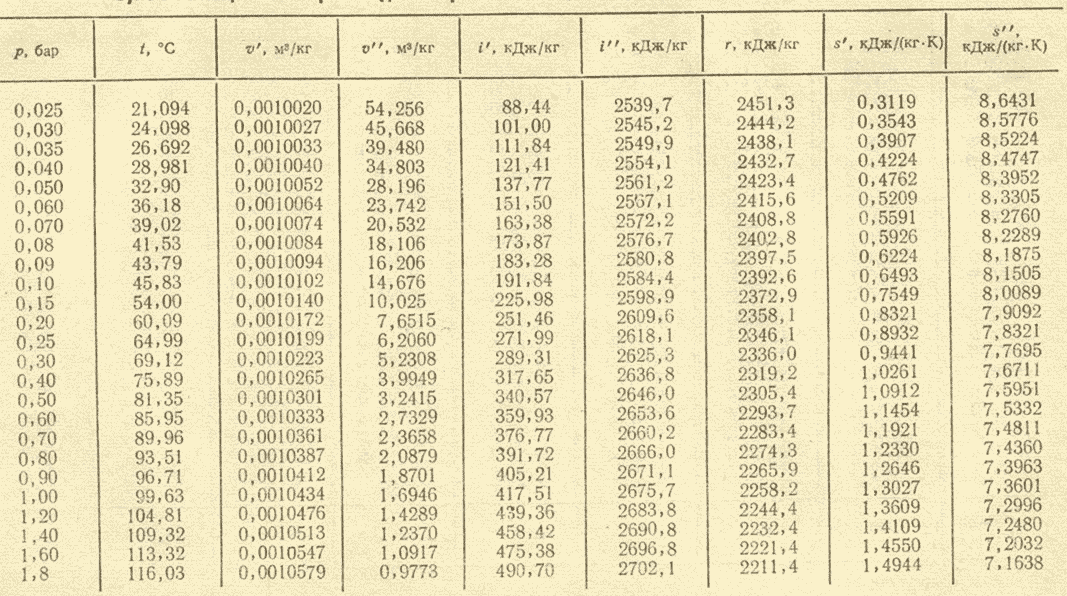 Продолжая
ранее
выполненный
в этом
разделе
расчет, по
которому рН
жидкости,
находящейся
в равновесии
с очищаемым
от SO2 газом,
равно 4, по
кинетической
кривой при рН
= 4 находим, что
за 2 мин в
раствор
переходит 7,3 г/л
СаО.
Это
эквивалентно
уловленным 8,3
г/л SO2, что
соответствует
62 % от
максимальной
химической
емкости
дистиллерной
суспензии по
этому
компоненту.
Продолжая
ранее
выполненный
в этом
разделе
расчет, по
которому рН
жидкости,
находящейся
в равновесии
с очищаемым
от SO2 газом,
равно 4, по
кинетической
кривой при рН
= 4 находим, что
за 2 мин в
раствор
переходит 7,3 г/л
СаО.
Это
эквивалентно
уловленным 8,3
г/л SO2, что
соответствует
62 % от
максимальной
химической
емкости
дистиллерной
суспензии по
этому
компоненту.
Очистка
топочных
газов от
диоксида
серы
дистиллерной
суспензией
является
процессом, в
основе
химизма
которого
лежит
необратимая
химическая
реакция,
приводящая к
образованию
осадка. При
разработке
математической
модели
аппарата для
реализации
этих
процессов
были приняты
следующие
допущения,
которые
позволили
упростить
расчет без
значительного
понижения
точности.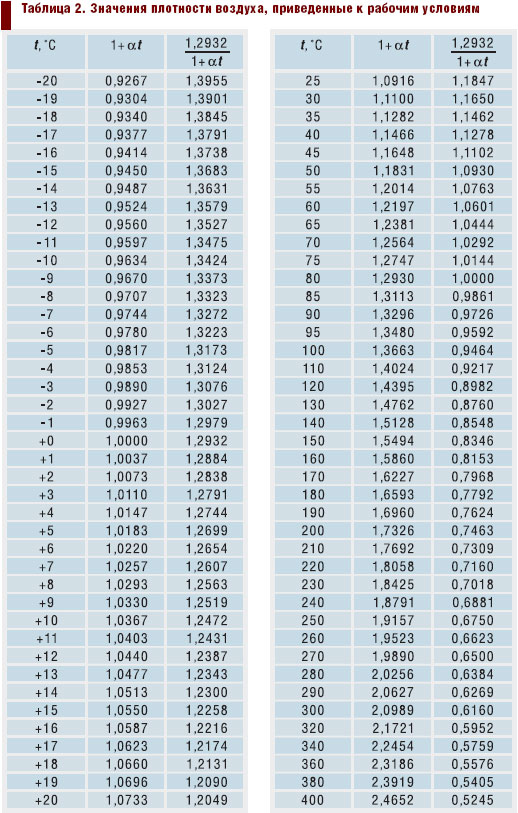
Первое допущение связано с линеаризацией рабочей линии. Оно основано на том, что из-за относительно небольшой концентрации распределяемых компонентов в газе в первом приближении можно принять, что расход газа по высоте колонны не меняется.
Второе допущение касается вида уравнения массопередачи. Как это принято для барботажных тарелок, будем считать жидкость на тарелке полностью перемешанной, а газ движущимся в режиме идеального вытеснения.
И
наконец
третье
допущение:
общее
давление в
аппарате
постоянно по
всей высоте.
Это не вносит
большой
ошибки, так
как
сопротивление
провальных
тарелок в
ожидаемых
режимах не
превышает 500
Па. При этом
общее
сопротивление
будет не
более 5500 Па, то
есть не более
5,5 % от
атмосферного
давления.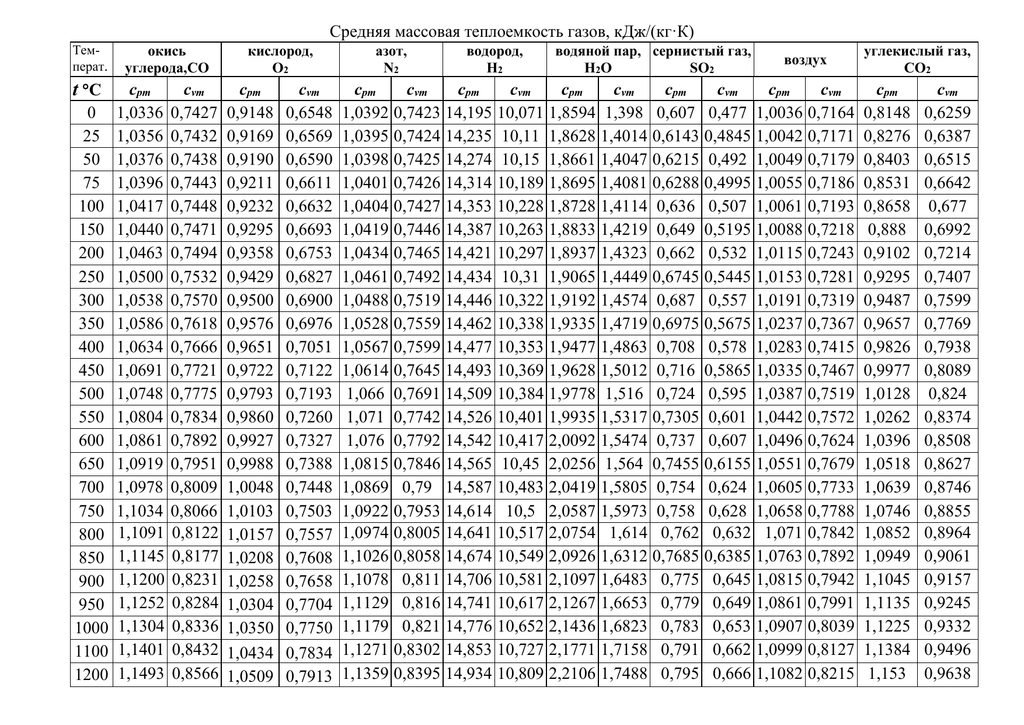
Схема материальных потоков, принятая в расчете, приведена на рис. 4.9. Построение математической модели аппарата для абсорбции диоксида серы дистиллерной суспензией в принципе не отличается от построения модели аппарата для абсорбции сероводорода. Поэтому уравнения рабочей линии (4.22) и кинетики процесса на i-той тарелке (4.23) отличий не имеют. Отличие имеется в формуле для расчета движущей силы процесса Dy, так как равновесное давление SO2 над дистиллерной суспензией равно нулю.
При принятых допущениях и обозначениях движущая сила абсорбции на одной тарелке
(5. 9)
9)
Из уравнения (4.23) после преобразований и подстановки в него (5.9) получим:
. (5.10)
При числе тарелок, равном n,
. (5.11)
Чтобы не
отсылать
читателя к
главе 4,
напомним, что
в формулах (5.9)
(5.11) мольный
расход газа обозначен
G моль/с; уi,
yi-1 мольная
доля
диоксида
серы в газе на
выходе и на
входе в
тарелку
соответственно;
а уk,
y0
мольная
доля
диоксида
серы в газе на
выходе и на
входе в
аппарат
соответственно;
S сечение
аппарата, м2; Р общее
давление на
тарелке, Па; Dу средняя
движущая
сила
абсорбции,
мольные доли; k
коэффициент
массопередачи,
моль/сПам2.
Формула (5.11) позволяет рассчитать концентрацию оксида серы на выходе из аппарата с числом тарелок, равным п , она, собственно, и является его математической моделью. Сравнивая ее с математической моделью для улавливания из газа сероводорода, можно видеть, что равенство нулю равновесного давления улавливаемого газа приводит к существенному упрощению математической модели аппарата. Этой же формулой можно воспользоваться для расчета количества диоксида углерода, поглощенного из газа одновременно с диоксидом серы. Только вместо коэффициента массопередачи k, рассчитанного по формуле (5.6), в последнем случае нужно воспользоваться формулой (5.7).
При
абсорбции SO2
дистиллерной
суспензией
большая
часть
активного
вещества Са(ОН)2
находится в
твердой фазе.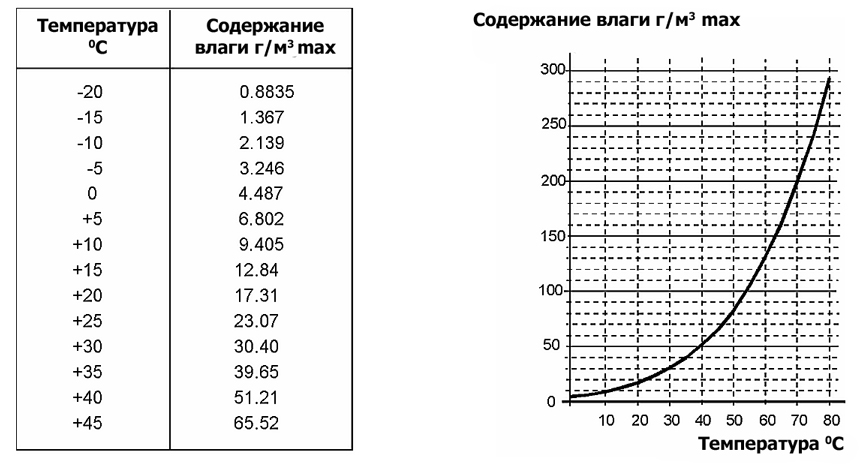 Как показано
выше, это
приводит к
тому, что при
относительно
больших
скоростях
абсорбции
растворение
гидроксида
кальция
становится
лимитирующей
стадией. В
принципе,
уравнение (5.6) учитывает
эту
особенность
процесса,
если
правильно
выбрать
коэффициенты
из таблицы 5.1.
Правда, при
этом расчет
числа
тарелок по
уравнению (5.11) усложняется,
так как
необходимо
рассчитывать
часть
аппарата, где
парциальное
давление
диоксида
серы больше 100
Па, отдельно
от части, где
меньше
этой
величины.
Как показано
выше, это
приводит к
тому, что при
относительно
больших
скоростях
абсорбции
растворение
гидроксида
кальция
становится
лимитирующей
стадией. В
принципе,
уравнение (5.6) учитывает
эту
особенность
процесса,
если
правильно
выбрать
коэффициенты
из таблицы 5.1.
Правда, при
этом расчет
числа
тарелок по
уравнению (5.11) усложняется,
так как
необходимо
рассчитывать
часть
аппарата, где
парциальное
давление
диоксида
серы больше 100
Па, отдельно
от части, где
меньше
этой
величины.
Расчет
можно
упростить,
если учесть,
что, как
показывает
опыт и
простые
расчеты, уже
на первой
тарелке
давление
диоксида
серы в газе
падает ниже 100 Па.
Поэтому,
рассчитав
одну тарелку
из условия
лимитирования
массопередачи
растворением
гидроксида
кальция,
остальные
можно
считать,
полагая
лимитирующим
сопротивление
газовой
пленки.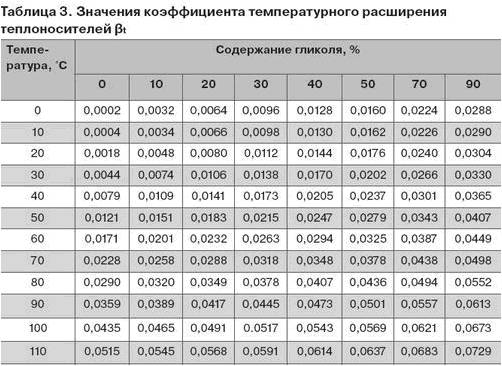
Для того
чтобы найти
скорость
абсорбции
диоксида
серы при
условии, что
определяющее
влияние на
нее
оказывает
скорость
растворения
шлама,
рассмотрим
следующий
упрощенный
механизм
процесса.
Диоксид серы
диффундирует
сквозь
газовую
пленку к
поверхности
жидкости, где
вступает в
реакцию с
растворенным
гидроксидом
кальция.
Последний
поступает в
зону реакции
в результате
растворения
твердого
вещества.
Сопротивление
переносу
диоксида
серы и
гидроксида
кальция в
зону реакции
отсутствует.
Такая модель,
безусловно,
сильно
упрощает
реальный
механизм
процесса,
который,
скорее всего,
включает
гидратацию
диоксида
серы,
диссоциацию
сернистой
кислоты,
реакцию
нейтрализации
и, возможно,
другие
стадии.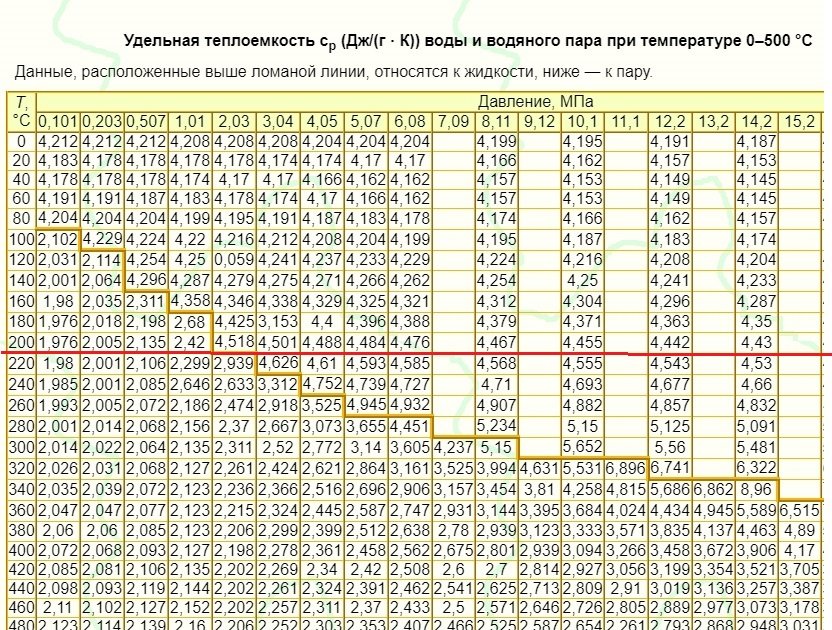 Однако, как
будет
показано
ниже, даже на
основании
упрощенного
механизма
удается
построить
удовлетворительную
кинетическую
модель.
Однако, как
будет
показано
ниже, даже на
основании
упрощенного
механизма
удается
построить
удовлетворительную
кинетическую
модель.
Запишем уравнения скорости процесса, отнесенной к 1 м2 поперечного сечения аппарата для каждой стадии, отвечающей предложенному механизму процесса.
1. Скорость транспорта диоксида серы через газовую пленку
, (5.12)
где парциальные давления диоксида серы в основной массе газа и на поверхности массопередачи соответственно, Па.
2. Равновесие на поверхности массопередачи
,
(5. 13)
13)
где концентрация диоксида серы в жидкости на поверхности массопередачи, моль/м3.
3. Скорость химической реакции:
, (5.14)
где константа скорости реакции, отнесенная к площади поперечного сечения аппарата, м4/мольс; концентрация гидроксида кальция в зоне реакции, моль/м3.
4. Скорость растворения гидроксида кальция равна скорости абсорбции диоксида серы:
, (5.15)
где ks
константа
скорости
растворения
шлама,
отнесенная к
поперечному
сечению
аппарата,
моль/м2с;
gшл
массовая
доля шлама в
дистиллерной
суспензии;
растворимость
гидроксида
кальция в
дистиллерной
суспензии,
моль/м3.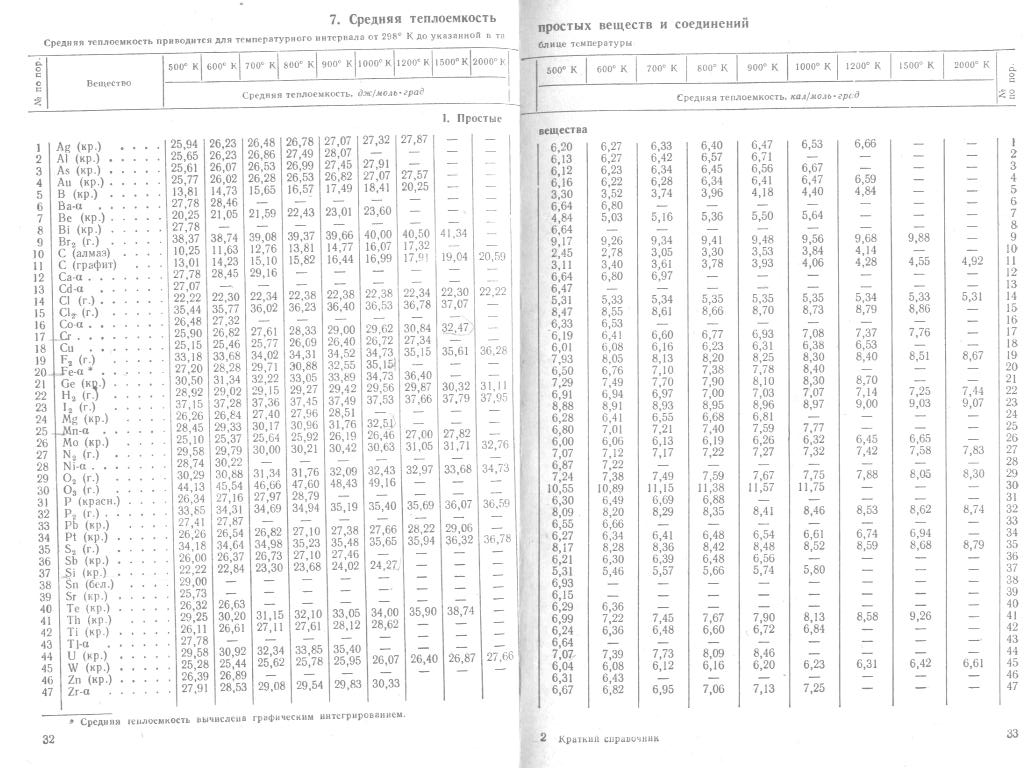
Исключив из системы уравнений (5.12) (5.15) величины и получим следующее уравнение:
. (5.16)
В
полученном
уравнении
есть две
величины: kр
и ks,
которые
определены
экспериментально.
При 20 оС:
kр
= 0,0113 м4/мольс
и ks
= 0,59 моль/м2с.
В расчете
принято:
= 22 моль/м3 [109
с. 57], Н =56,6 Пам3/моль
(рассчитано
по данным
справочника [110]).
Значение kг
рассчитывали
по формуле (5.6) с
коэффициентами
из табл. 5.1 (первая
строка).
Точность
расчета
скорости
абсорбции по
уравнению
(5.16) характеризуется
остаточной
СКО 5,510-3
моль/м2с
и
коэффициентом
корреляции
эксперимента
с расчетом 0,98.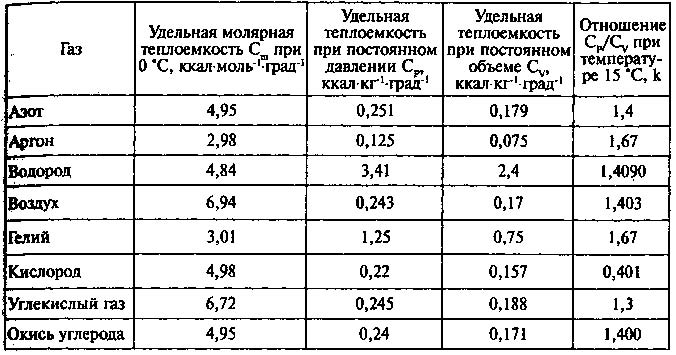
Расчет при других температурах можно выполнять, учитывая, что, как показано выше, кинетика абсорбции диоксида серы дистиллерной суспензией не зависит от температуры. Поэтому допустимо принять, что произведение и комплекс не зависят от температуры и
= 12,9, а = 2922. (5.17)
Таким образом, расчетное уравнение для определения скорости абсорбции на первой по ходу газа тарелке будет иметь вид:
. (5.18)
Поскольку
при
определении
надо знать
парциальное
давление
диоксида
серы на
выходе из
тарелки, а его
можно
рассчитать
по уравнению
материального
баланса, лишь
зная
скорость
абсорбции,
уравнение (5.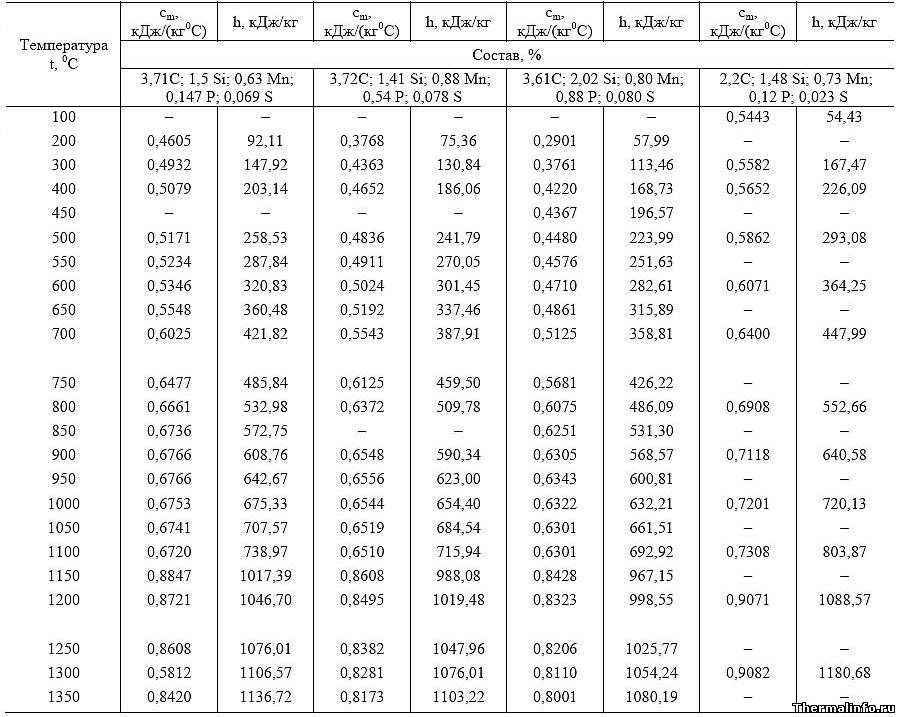 18) необходимо
решать
методом
последовательных
приближений.
18) необходимо
решать
методом
последовательных
приближений.
Расчет и соответственно математическое моделирование процесса очистки газа от диоксида серы дистиллерной суспензией не ограничивается моделью процесса абсорбции. Дело в том, что по технологическим условиям суспензия подается в аппарат с температурой 9095 оС. Взаимодействуя с газом, она будет охлаждаться, а газ насыщаться влагой.
Обычно в расчете аналогичных аппаратов, где происходит испарение жидкости, контактирующей с горячим газом (например, сушилок, башен для грануляции и т.п.) прибегают к совместному решению уравнений тепло- и массопереноса:
G cг dt = aг
(ti t) dS;
(5.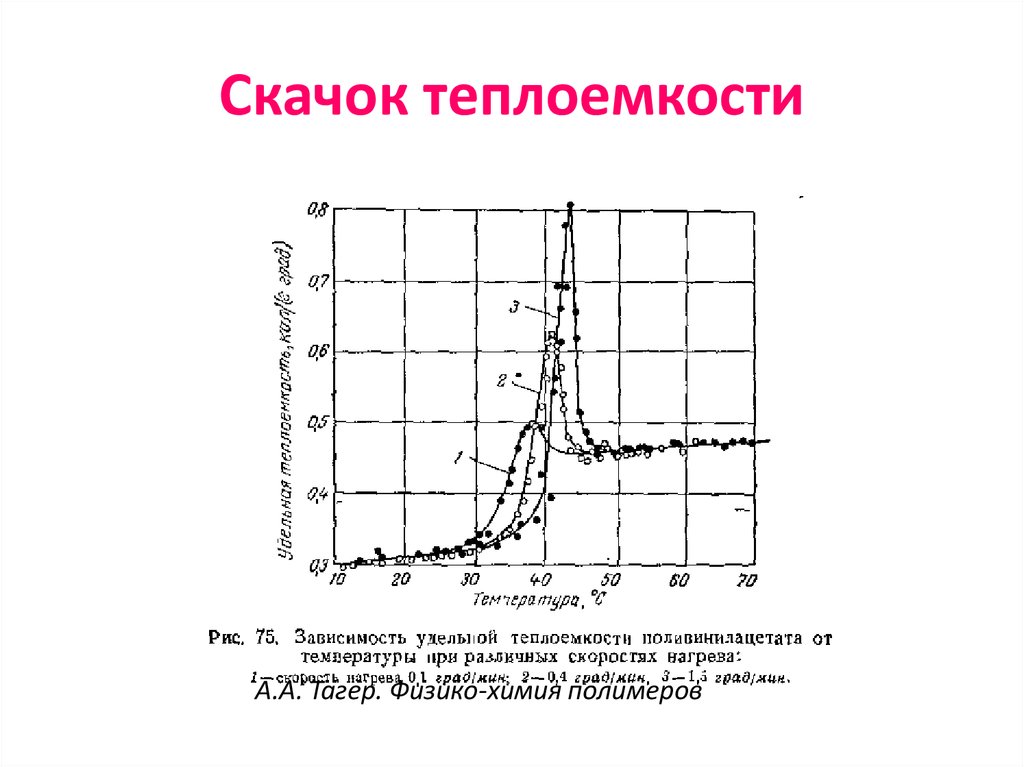 19)
19)
G dx = kг (xi x) dS, (5.20)
где
G массовый
расход газа
кг/с; cг
теплоемкость
газа, кДж/кг
град; ti, t
температуры
поверхности
раздела газ-жидкость
и основной
массы газа,
соответственно,
оС; S
поверхность
контакта фаз,
м2; xi,
x
влагосодержание
газа,
равновесного
с жидкостью
на
поверхности
раздела фаз и
основной
массы газа
соответственно,
кг/кг; aг
коэффициент
теплоотдачи
со стороны
газовой фазы,
вт/м2град;
kг
коэффициент
массопередачи,
кг/м2с.
При этом общая скорость переноса теплоты к жидкости с учетом теплоты конденсации составляет:
L cг dtг = [aг (t ti) + r kг (x xi)] dS, (5.21)
где r теплота парообразования, кДж/кг; cг теплоемкость жидкости, кДж/кг град.
Несмотря
на кажущуюся
простоту
уравнения (5.21), его
интегрирование
оказывается
достаточно
сложным из-за
того, что
величины ti
и xi -
неизвестны и
к тому же
функционально
зависимы
друг от друга.
В результате
к решению
необходимо
привлекать
уравнение
теплоотдачи
в жидкой фазе,
что приводит
к достаточно
сложной
модели,
решение
которой
рационально
выполнять
только с
применением
ЭВМ.
Интересный подход был предложен Меркелем и Хиршем [111] для проектирования градирен. Ими было показано, что использование движущей силы, выраженной в единицах энтальпии, приводит к существенному упрощению расчетов. Суть предложения сводилась к следующему. Уравнение (5.21) можно преобразовать к виду:
L cг dtг = kг[aгcг(t ti)/kгcг + r (x xi)] dS. (5.22)
Отношение
aг/kгcг
в
формуле (5.22) носит
название
психрометрический
коэффициент
и известно из
теории мокрого
термометра.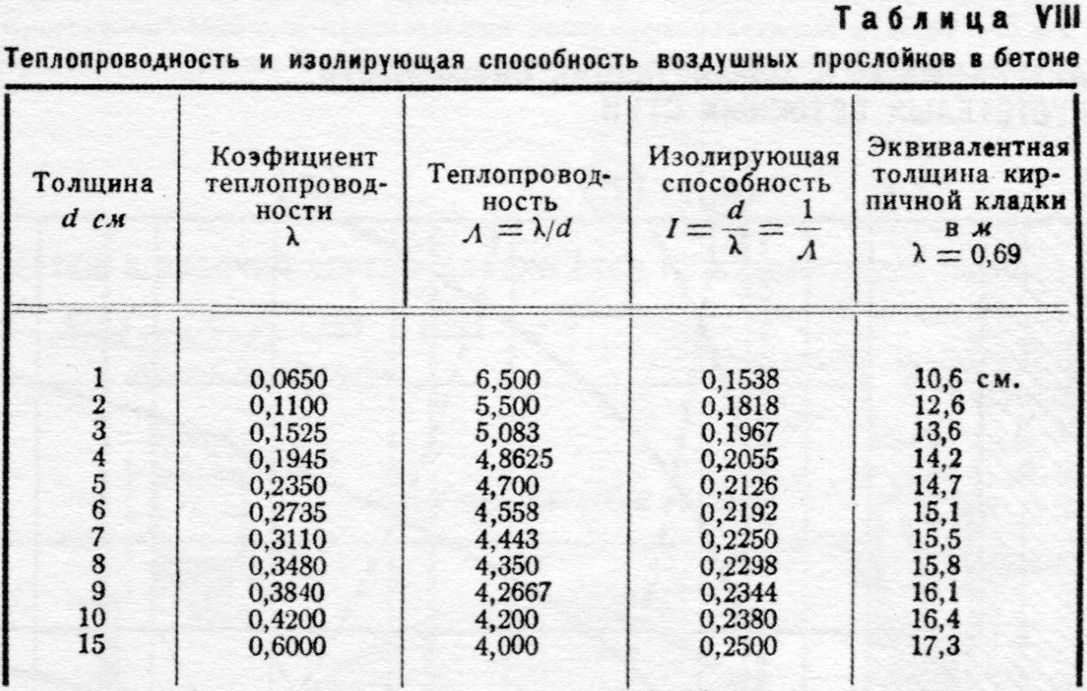 Как
показывают
многочисленные
опыты [112],
для системы
вода воздух
и близких к
ней по
физическим
свойствам,
например,
вода
дымовые газы,
дистиллерная
суспензия
дымовые газы
значение
указанного
отношения
близко к
единице.
Тогда (5.22) можно
переписать
следующим
образом:
Как
показывают
многочисленные
опыты [112],
для системы
вода воздух
и близких к
ней по
физическим
свойствам,
например,
вода
дымовые газы,
дистиллерная
суспензия
дымовые газы
значение
указанного
отношения
близко к
единице.
Тогда (5.22) можно
переписать
следующим
образом:
L cг dtг = kг[(cг t + r x) (cг ti + r xi)] dS. (5.23)
Если
учесть, что
энтальпия
влажного
воздуха Нг
= cгt + rx и
уравнение
баланса
энергии L cг
dtг = G dНг,
то из (5. 23) становится
очевидным,
что скорость
обмена
теплотой
между
жидкостью и
газом
пропорциональна
разности
энтальпий
основной
массы газа и
газа,
равновесного
с
охлаждающей
жидкостью на
поверхности
раздела фаз с
коэффициентом
пропорциональности,
равным kг.
То есть
23) становится
очевидным,
что скорость
обмена
теплотой
между
жидкостью и
газом
пропорциональна
разности
энтальпий
основной
массы газа и
газа,
равновесного
с
охлаждающей
жидкостью на
поверхности
раздела фаз с
коэффициентом
пропорциональности,
равным kг.
То есть
G = kг (Нг Нi). (5.24)
Таким
образом,
упрощение
модели
достигается
за счет того,
что система (5.19) ,
(5.20) заменяется
одним
уравнением (5.24). Тем не менее,
рассмотренный
выше подход
не устраняет
неопределенности
относительно
температуры
жидкости и
газа на
поверхности
раздела фаз и
соответственно
равновесной
энтальпии
газа.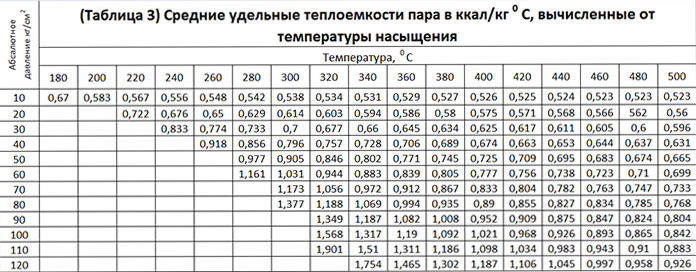 Для
преодоления
этой
неопределенности
по аналогии с
массопередачей
выразим
общую
движущую
силу
переноса
энергии
между газом и
жидкостью в
единицах
энтальпии. То
есть
представим
общую
движущую
силу как сумму
отдельных
движущих сил
в газовой и
жидкой фазах:
Для
преодоления
этой
неопределенности
по аналогии с
массопередачей
выразим
общую
движущую
силу
переноса
энергии
между газом и
жидкостью в
единицах
энтальпии. То
есть
представим
общую
движущую
силу как сумму
отдельных
движущих сил
в газовой и
жидкой фазах:
G dНг = L dНж = L сж dtж = Кн (Н* Нг) dS, (5.25)
где Н* энтальпия газа, равновесного с основной массой охлаждающей жидкости, кДж/кг,
причем
H*
Hг = (Hi
Hг)
+ (H* Hi)
(5. 26)
26)
, (5.27)
где aж коэффициент теплоотдачи от поверхности раздела фаз в основную массу жидкости.
В работе [113]
найдено, что в
зависимости
от условий
протекания
процесса (отношения
L/G и tж)
сопротивление
переносу
энтальпии со
стороны
жидкости,
которое
характеризуется
величиной (1/aж)[(H*
Hi)/(tж – ti)]
составляет 2746 %
от общей
величины
сопротивления,
причем эта
доля
снижается с
ростом
плотности
орошения
жидкостью и
снижением
температуры.
Там же
найдено, что
для
насадочных
колонн
отношение aж/kг
растет
пропорционально
L0,43.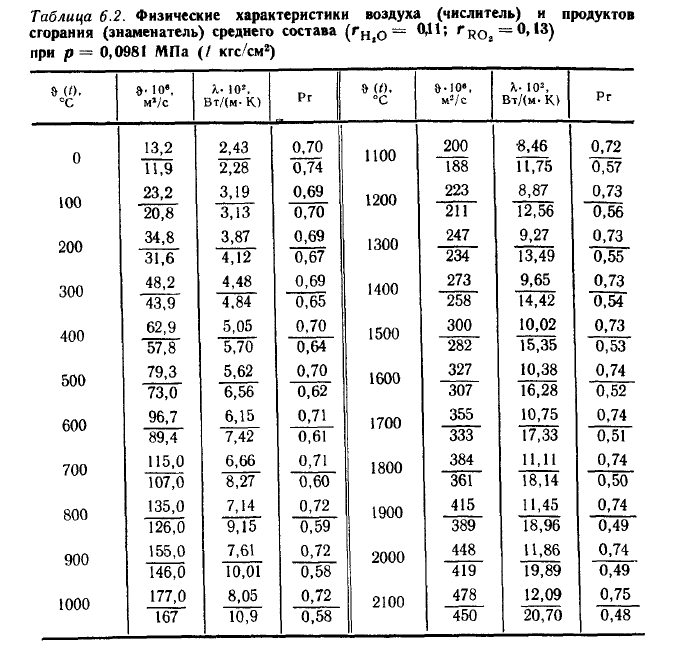
Таким образом, сопротивление переносу энергии со стороны жидкости достаточно велико и его нельзя игнорировать, а следовательно, пользоваться данными о массоотдаче в газовой фазе для расчета переноса энтальпии. Тем не менее, можно показать, что поскольку массопередача при абсорбции диоксида серы при < 100 Па контролируется газовой пленкой, то коэффициент массопередачи, рассчитанный по уравнению (5.6) , может быть легко перессчитан в величину Кн из уравнения (5.25) . Действительно, результаты исследования массопередачи обобщались нами, исходя из обычного уравнения массопереноса:
G dx = kг (
рп)
dS,
(5. 28)
28)
где и рп равновесное давление улавливаемого компонента над основной массой жидкости и его парциальное давление в газе соответственно, Па.
Влагосодержание газа х связано с его парциальным давлением известным [114] соотношением: x = 0,622 рп/(Pобщ рп), где Pобщ общее давление. Учитывая, что в интервале температур 2050 оС давление рп не превышает 10 % величины Pобщ, можно принять в первом приближении, что x @ 0,622 рп /Pобщ. Тогда энтальпийную движущую силу можно выразить через парциальное давление водяного пара следующим образом:
H*
Hг = cг(tж
tг) + 0,622 r
(
рп)/Pобщ
(5.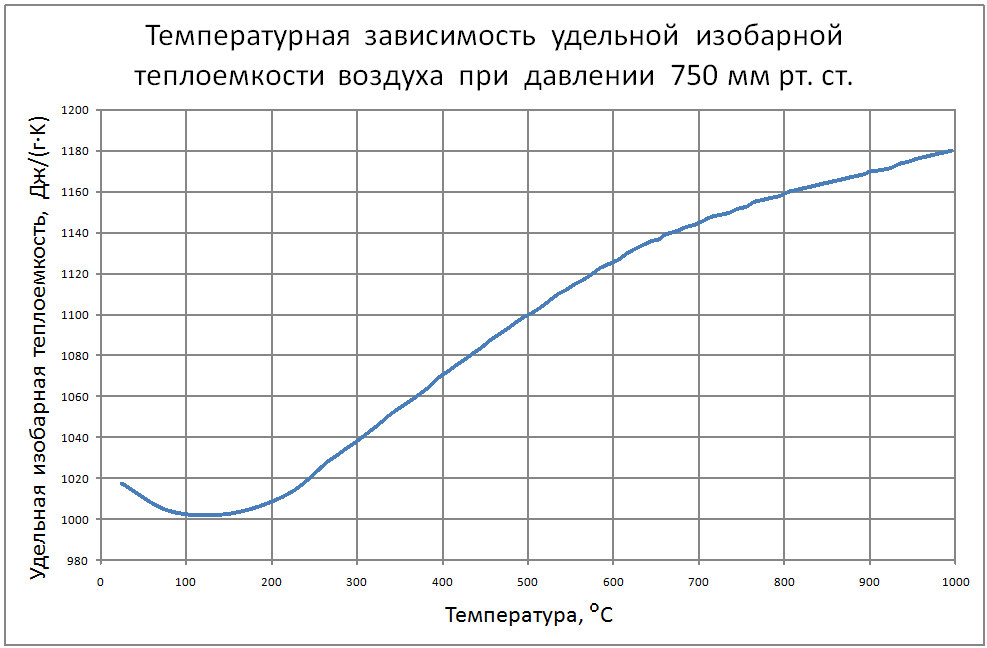 29)
29)
Обычно при непосредственном контакте газа и жидкости значение tж tг не превышает 20 оС, соответственно cг(tж tг) > 5 кДж/кг. В аналогичных температурных условиях значение 0,622r( – рп)/Pобщ составляет около 100 кДж/кг, то есть величину, на два порядка большую. Поэтому членом cг(tж tг) в уравнении (5.29) можно пренебречь, и окончательно получим:
H* Hг 0,622 r ( рп) / Pобщ . (5.30)
Теперь,
подставив (5.30) в
(5.25) и поделив (5.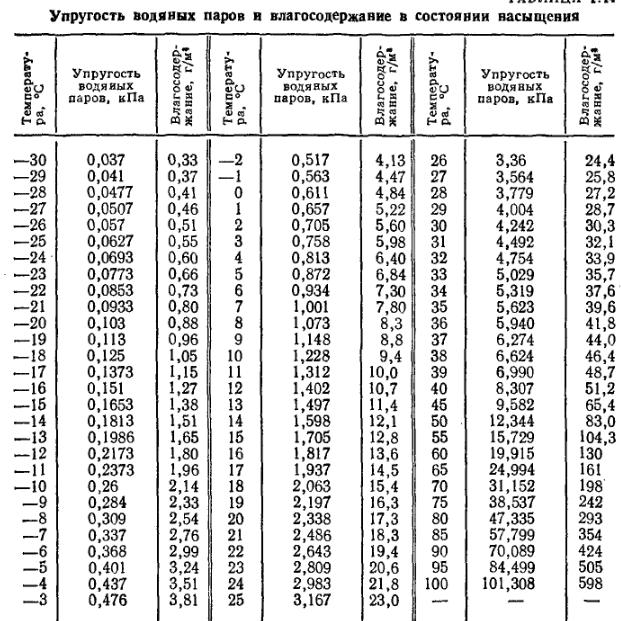 28) на результат
подстановки,
учитывая, что G
dHг = G r dx, в
результате
преобразований
получим:
28) на результат
подстановки,
учитывая, что G
dHг = G r dx, в
результате
преобразований
получим:
Кн = kг Робщ / 0,622 . (5.31)
Следующий вопрос, который возникает после того, как мы определились с основным дифференциальным уравнением, описывающим процесс (уравнение (5.25) с коэффициентом Кн из (5.31) ), является вопрос о структуре алгоритма расчета математической модели холодильника газа.
Трудность
заключается
в том, что, во-первых,
уравнение (5.25) – нелинейное,
причем эта
нелинейность
определяется
нелинейностью
функции H* = f(tж),
и его
необходимо
решать
численными
методами; во-вторых,
поскольку
аппарат для
очистки газа
от диоксида
серы
является
противоточным
аппаратом,
часть
исходных
данных для
расчета
заданы на
входе газа, а
часть на
противоположном
конце
аппарата, на
входе
жидкости.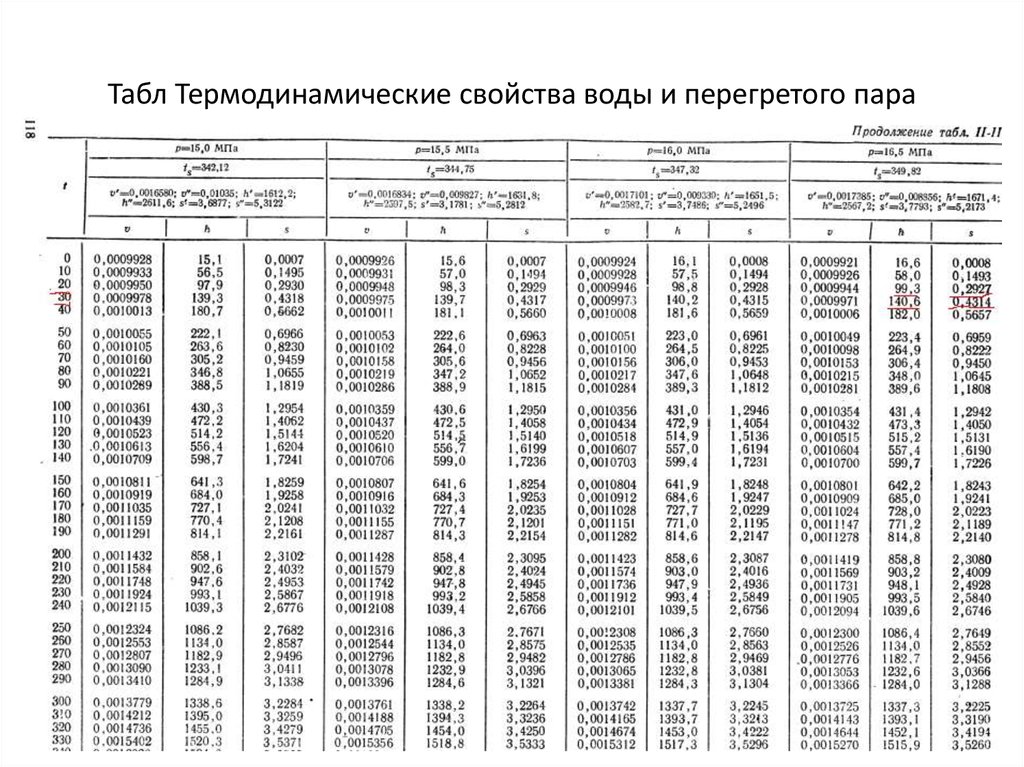 При
расчете
аппаратов со
ступенчатым
контактом
фаз
рекомендуют [115],
введя ряд
допущений, в
частности, о
линейности
равновесной
кривой на
протяжении
одной
ступени
контакта и/или
об идеальном
перемешивании
жидкости на
ней, свести
задачу к
замене
дифференциального
уравнения
процесса
системой
алгебраических
и решать эту
систему
методом
итераций. При
этом по
технологическим,
балансным
или иным
соображениям
назначают
величины
параметров
жидкости и
газа на входе
газа в
аппарат.
Производят
потарелочный
расчет
аппарата от
первой
тарелки,
считая снизу,
до последней.
Полученные в
расчете
параметры
жидкости
сравнивают с
заданными на
входе
жидкости в
аппарат и,
если
расхождение
рассчитанных
и заданных
параметров
окажется
слишком
большим,
исходные
данные
корректируют,
и расчет
повторяют.
При
расчете
аппаратов со
ступенчатым
контактом
фаз
рекомендуют [115],
введя ряд
допущений, в
частности, о
линейности
равновесной
кривой на
протяжении
одной
ступени
контакта и/или
об идеальном
перемешивании
жидкости на
ней, свести
задачу к
замене
дифференциального
уравнения
процесса
системой
алгебраических
и решать эту
систему
методом
итераций. При
этом по
технологическим,
балансным
или иным
соображениям
назначают
величины
параметров
жидкости и
газа на входе
газа в
аппарат.
Производят
потарелочный
расчет
аппарата от
первой
тарелки,
считая снизу,
до последней.
Полученные в
расчете
параметры
жидкости
сравнивают с
заданными на
входе
жидкости в
аппарат и,
если
расхождение
рассчитанных
и заданных
параметров
окажется
слишком
большим,
исходные
данные
корректируют,
и расчет
повторяют. Так
поступают до
тех пор, пока
расчет и
задание не
совпадут с
заданной
точностью.
Так
поступают до
тех пор, пока
расчет и
задание не
совпадут с
заданной
точностью.
Рассмотрим преобразование дифференциального уравнения (5.25) в систему алгебраических уравнений. Для этого примем, что в пределах одной тарелки жидкость полностью перемешана, а газ движется в поршневом режиме (идеальное вытеснение). Такая модель структуры потоков близка к реальной для крупноперфорированых противоточных тарелок, которые устанавливают в газоочиститель. Тогда уравнение (5.25) в пределах одного контактного устройства имеет аналитическое решение:
G(Hг,i-1
Hг,i) = КнS (Hг,
i-1Hг, i) / ln
,
(5.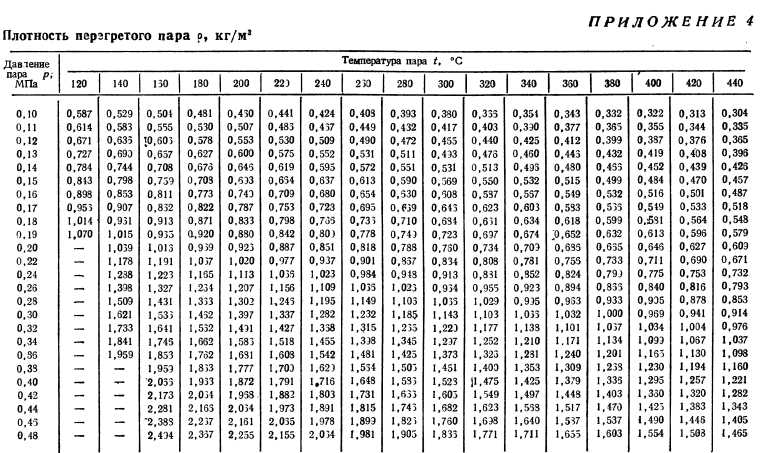 32)
32)
откуда:
Hг, i = , (5.33)
где i номер тарелки.
Ниже
описан
алгоритм и
программа
расчета
математической
модели
аппарата,
которая
пригодна не
только для
расчета
теплообмена
между
очищаемым
газом и
дистиллерной
суспензией,
но и для
любого
процесса
контактного
охлаждения
газа,
содержащего
один
конденсирующийся
компонент,
например,
водяной пар.
Алгоритм
предназначен
для
проектного
или
поверочного
расчетов, а
именно,
определения
числа
контактных
ступеней для
достижения
заданной
степени
охлаждения
газа или
определения
степени
охлаждения
газа при
заданном
числе
контактных
ступеней и
расходе
охлаждающей
жидкости.
Исходными данными для расчета являются:
для газа:
– теплоемкость сухой части газа сг, кДж/кг оС;
– общее давление (абсолютное) Poбщ, Па;
– влагосодержание исходного газа х, кг/кг сухой части;
– теплосодержание (энтальпия) газа Hг, o, кДж/кг, или его температура tг, o, оС;
– расход газа G, кг/ч.
для жидкости:
– теплоемкость сж, кДж/кг оС;
– нормальная температурная депрессия D, оС;
– температура жидкости tж, оС;
– расход жидкости L, кг/ч;
В случае
поверочного
расчета
дополнительно
задается
число
контактных
ступеней. Для
проектного
расчета в
задание
входит
теплосодержание
или
температура
выходящего
газа.
Для
проектного
расчета в
задание
входит
теплосодержание
или
температура
выходящего
газа.
Алгоритмом предусмотрена возможность задания эффективности контактного элемента по Мерфи (см. например [112]). В этом случае коэффициент массопередачи не вычисляется, и алгоритм реализует метод “теоретических тарелок” (см. например [116]).
Как
видно из
набора
исходных
данных, при
проведении
проектного
расчета для
сечения
аппарата,
соответствующего
входу газа,
заданы или
могут быть
определены
из
материального
баланса все
параметры
контактирующих
сред. Поэтому
расчет
выполняется
за один
проход. При
разработке
алгоритма
использован
метод Эйлера [117].
Применительно
к
рассматриваемому
случаю он
заключается
в том, что по
исходным
данным и
рассчитанной
температуре
выходящей из
аппарата
охлаждающей
жидкости с
использованием
уравнений (5.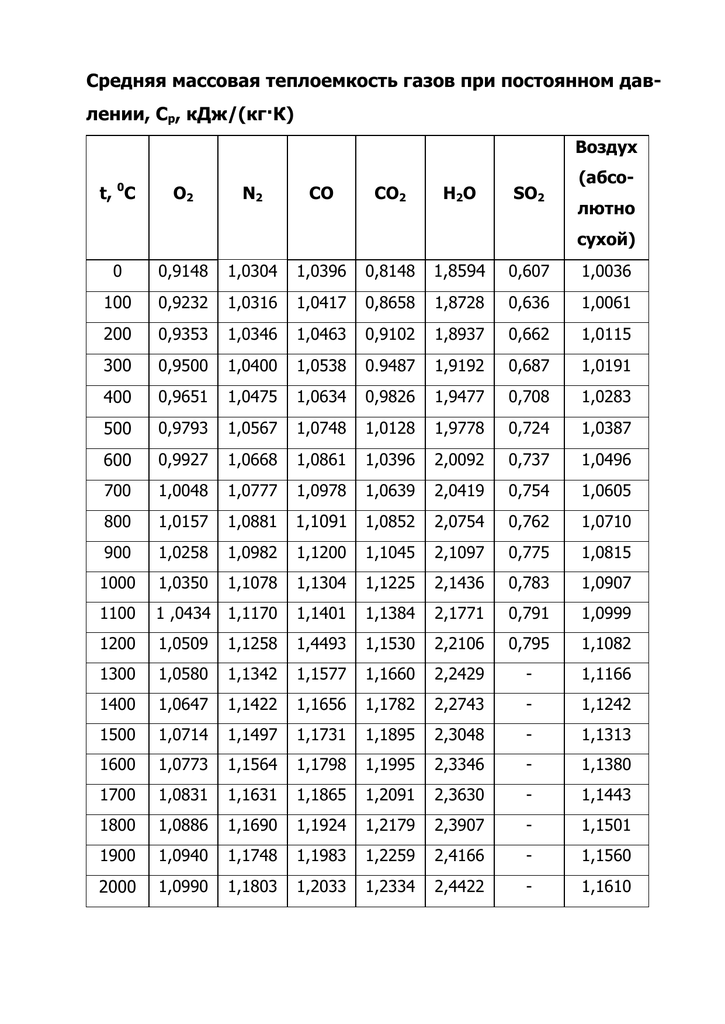 33) и теплового
баланса
тарелки (уравнения
рабочей
линии)
вычисляют
параметры
газа на
выходе из
первой,
считая снизу,
тарелки и
жидкости на
входе в нее.
По этим
данным
рассчитывают
следующую
тарелку и
продолжают
расчет до тех
пор, пока
значение
энтальпии
газа на
выходе из i-той
тарелки не
окажется
ниже
заданной
величины для
охлажденного
газа. Расчет
прекращается,
а его
результаты
могут быть
проиллюстрированы
графиком в
координатах:
температура
охлаждающей
жидкости
теплосодержание
газа, а также
распечатаны
в виде
таблицы со
значениями
параметров
газа и
жидкости на
каждой
тарелке.
33) и теплового
баланса
тарелки (уравнения
рабочей
линии)
вычисляют
параметры
газа на
выходе из
первой,
считая снизу,
тарелки и
жидкости на
входе в нее.
По этим
данным
рассчитывают
следующую
тарелку и
продолжают
расчет до тех
пор, пока
значение
энтальпии
газа на
выходе из i-той
тарелки не
окажется
ниже
заданной
величины для
охлажденного
газа. Расчет
прекращается,
а его
результаты
могут быть
проиллюстрированы
графиком в
координатах:
температура
охлаждающей
жидкости
теплосодержание
газа, а также
распечатаны
в виде
таблицы со
значениями
параметров
газа и
жидкости на
каждой
тарелке.
При
проведении
поверочного
расчета
задано число
ступеней
контакта, но
неизвестна
энтальпия
выходящего
газа. Поэтому
нельзя
рассчитать
температуру
выходящей из
аппарата
жидкости и
провести
расчет, как
было описано
выше. В этом
случае
расчет
ведется
итеративно.
Задается
нулевое
приближение
указанной
температуры,
и расчет
ведут так же,
как и при
проектном
расчете,
однако,
вычисления
прекращаются
после
расчета
последней
тарелки,
число
которых в
данном
случае
задано.
Расчетное
значение
температуры
дистиллерной
суспензии на
входе в эту
тарелку
сравнивается
с заданным и,
если
расхождение
велико (в
рассматриваемом
алгоритме
превышает 0,5 оС),
подбирают
лучшее
приближение
температуры
выходящей
жидкости, и
расчет
повторяют.
Подбор
температуры
выходящей
жидкости
выполняется
методом
деления
отрезка
пополам [117].
Поэтому
нельзя
рассчитать
температуру
выходящей из
аппарата
жидкости и
провести
расчет, как
было описано
выше. В этом
случае
расчет
ведется
итеративно.
Задается
нулевое
приближение
указанной
температуры,
и расчет
ведут так же,
как и при
проектном
расчете,
однако,
вычисления
прекращаются
после
расчета
последней
тарелки,
число
которых в
данном
случае
задано.
Расчетное
значение
температуры
дистиллерной
суспензии на
входе в эту
тарелку
сравнивается
с заданным и,
если
расхождение
велико (в
рассматриваемом
алгоритме
превышает 0,5 оС),
подбирают
лучшее
приближение
температуры
выходящей
жидкости, и
расчет
повторяют.
Подбор
температуры
выходящей
жидкости
выполняется
методом
деления
отрезка
пополам [117]. Вся
процедура
повторяется
до тех пор,
пока
расчетное и
заданное
значения
температуры
жидкости на
входе в
аппарат не
совпадут с
указанной
выше
точностью.
Результаты
расчета
оформляются
так же, как и в
предыдущем
случае.
Вся
процедура
повторяется
до тех пор,
пока
расчетное и
заданное
значения
температуры
жидкости на
входе в
аппарат не
совпадут с
указанной
выше
точностью.
Результаты
расчета
оформляются
так же, как и в
предыдущем
случае.
Рассмотрим
подробней
структуру
алгоритма
поверочного
расчета, как
более
сложного.
Вначале
находят
температуру
равновесной,
с приходящим
газом,
охлаждающей
жидкости, то
есть
температуру
мокрого
термометра,
выше которой
охлаждающая
жидкость не
может быть
нагрета
данным газом.
Расчет
выполняется
итеративно,
то есть
задают
приближенное
значение
искомой
температуры tj,
вычисляют
соответствующее
ей
теплосодержание
газа Hг и
сравнивают с
заданным,
если
расхождение
превышает 1
кДж / кг
приближение
корректируют,
и расчет
повторяют до
достижения
указанной
точности.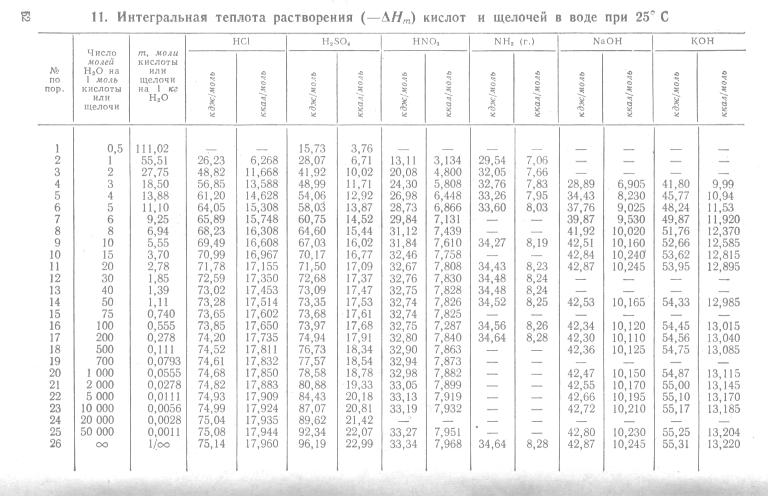 Поскольку
интересующая
нас
температура
находится в
интервале 0100
оС, первый
расчет
выполняют
для
температуры 50
оС в
следующей
последовательности.
Используя
заданное
значение
нормальной
температурной
депрессии D
для жидкости,
подаваемой в
газоочистной
аппарат,
рассчитывают
температуру
насыщенного
пара чистой
воды над
раствором
данной
температуры.
Используется
формула
Тищенко [116
]. Для этого
вычисляют
вспомогательные
величины:
Поскольку
интересующая
нас
температура
находится в
интервале 0100
оС, первый
расчет
выполняют
для
температуры 50
оС в
следующей
последовательности.
Используя
заданное
значение
нормальной
температурной
депрессии D
для жидкости,
подаваемой в
газоочистной
аппарат,
рассчитывают
температуру
насыщенного
пара чистой
воды над
раствором
данной
температуры.
Используется
формула
Тищенко [116
]. Для этого
вычисляют
вспомогательные
величины:
а = 2510 + 2,538 tj + 8,85 D / (2,538 0,0162 D), (5.34)
б = 2510 tj
1209 D
/ (2,538 0,0162 D).
(5.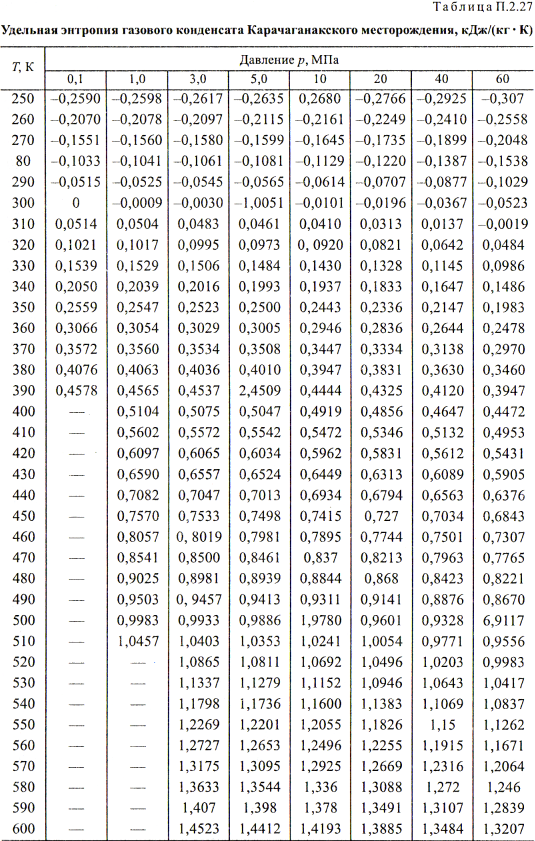 35)
35)
и собственно искомую температуру :
= а/2 а2/4 б (5.36)
Рассчитывают парциальное давление водяного пара Pп для этой температуры по формуле Ренкина (2.3) , затем определяют теплосодержание водяного пара Hп (используют методы расчета физико-химических величин из [118]) и собственно теплосодержание газа Hг:
Hп = 2483,9 + 1,989 tj 6,633710-5pп ; (5.37)
Hг
= сгtj
+ 0,8041 pп
Hп
/ (Poбщ
pп)
rс.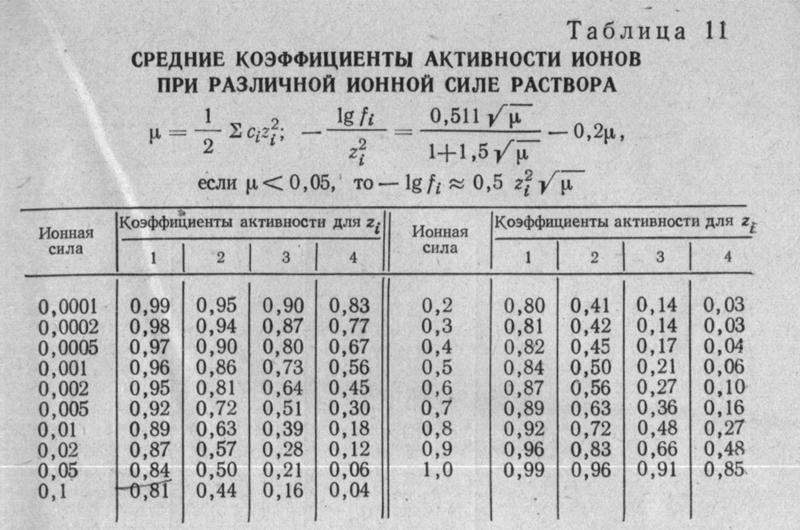 г .
(5.38)
г .
(5.38)
где rс.г – плотность сухой части газа, кг/м3.
Если
рассчитанное
значение Hг
меньше
заданного, к
нулевому
приближению
температуры (напомним,
что при
первой
итерации это
50 оС)
добавляют
50 / 2 = 25 оС, если
больше, то
эту же
величину
вычитают из tj,
получают
новое
приближение tj
и повторяют
расчет Hг.
Если и теперь Hг
отличается
от заданной
величины, tj
опять
изменяют, как
было
указанно
выше, но
прибавляют
или вычитают
уже 25 : 2 = 12,5 оС.
Так, деля на
каждом шаге
добавку
пополам и
корректируя tj,
если Hг
меньше
заданного,
вверх, а если
больше вниз,
и повторяя
расчет Hг,
добиваются
равенства
расчета и
задания с
точностью до
единицы.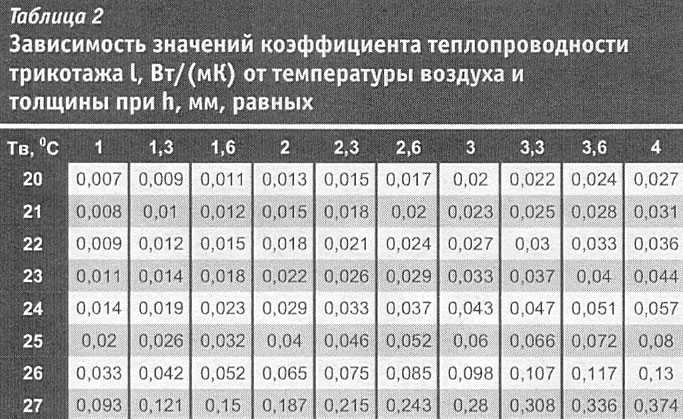 Найденную в
результате
величину tj
считают
равновесной
с входящим
газом,то
есть tj =
.
Найденную в
результате
величину tj
считают
равновесной
с входящим
газом,то
есть tj =
.
Теперь находят нулевое приближение температуры жидкости на выходе из газоочистного аппарата tж, o, в качестве которого используется среднеарифметическое значение температур жидкости, входящей в аппарат tж, n+1, и найденной в предыдущем расчете . Определяют также исходный шаг корректировки этой величины А = ( tж, n+1) / 2. Затем находят теплосодержание газа, равновесного с охлаждающей жидкостью при температуре tж,n+1, по формулам (5.34) (5.38) и теплосодержание газа, покидающего аппарат, Hг,n по уравнению рабочей линии:
Hг, n=
сжL(tж, n+1 tж,
o)/G + Hг,о .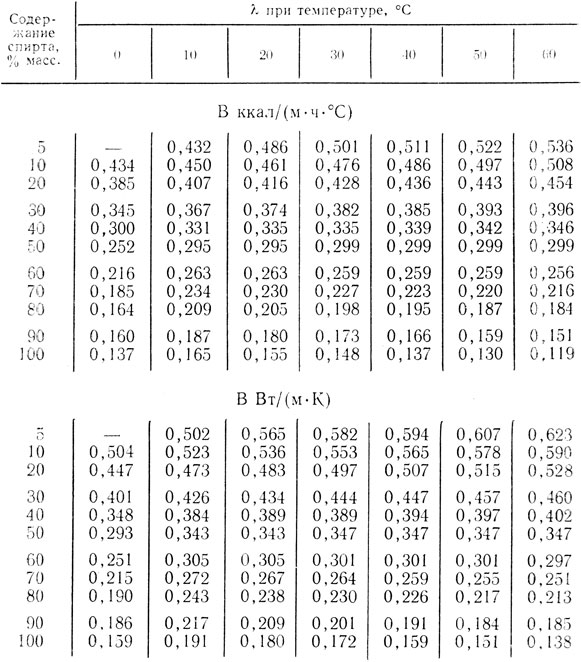 (5.39)
(5.39)
Далее идет проверка допустимости нулевого приближения tж, o по условию совпадения знаков разностей Hг, n Hг, о и Hг, n. Если условие выполняется, то расчет продолжают, если нет, то tж, o сразу уменьшают на величину А/2, и возвращаются к расчету Hг, n (формула (5.33)).
В случае совпадения знаков приведенных выше разностей начинают потарелочный расчет аппарата. По формулам (5.34) (5.38) находят теплосодержание газа, равновесного с жидкостью на данной тарелке, , затем по формуле (5.33) теплосодержание газа, покидающего тарелку Hг,i, температуру жидкости на входе в тарелку (по уравнению рабочей линии):
tж, i
= tж, o + G (Hг,i Hг,о)
/ сж L.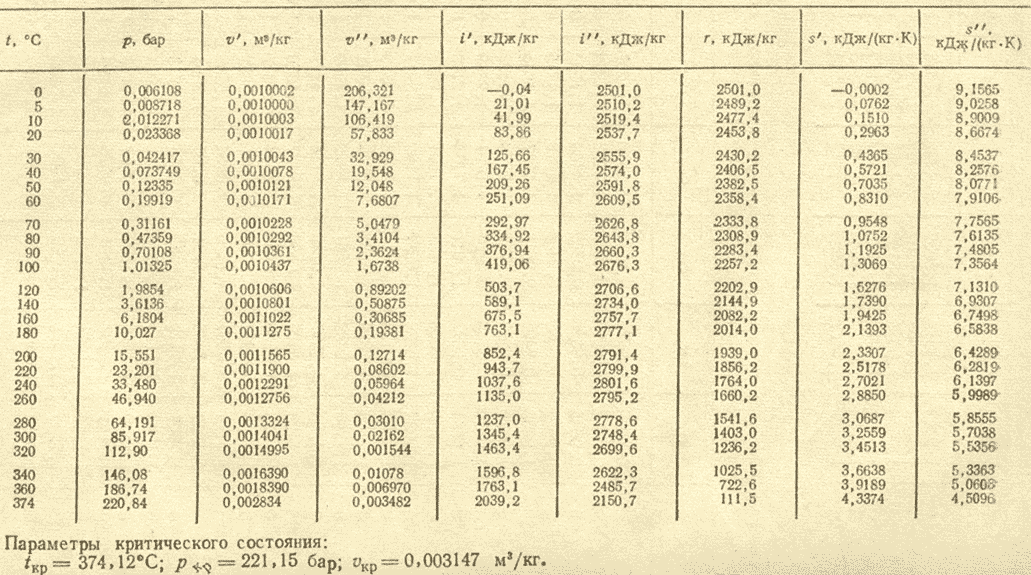 (5.40)
(5.40)
Расчет
по формулам (5.33)
(5.40) повторяют
для каждой
тарелки, пока
их число не
достигнет
заданного
для данного
аппарата
числа n.
После этого
проводят
проверку
знака и
абсолютной
величины
разности
расчетной
температуры
входящей
жидкости tж,
n+1 и
заданного ее
значения.
Если
абсолютная
величина
этой
разности
меньше 0,5 оС,
расчет
прекращают и
переходят к
печати
результатов,
в противном
случае
расчет
повторяют со
скорректированным
значением tж,o
.
Корректировку
осуществляют
следующим
образом: tж,o
увеличивают
на
А/2, если
указанная
выше
разность
отрицательна,
и уменьшают
на эту же
величину,
если
положительна.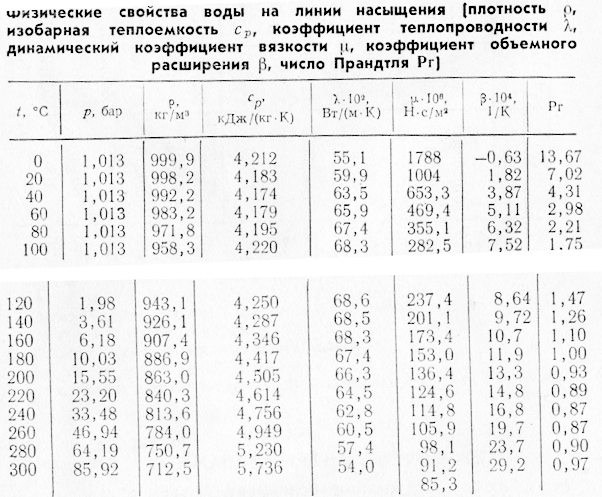 Перед
началом
каждой
следующей
итерации
величину А
заменяют на А/2.
Перед
началом
каждой
следующей
итерации
величину А
заменяют на А/2.
Заводские испытания являются заключительным этапом научной разработки. Испытания опытной установки для отработки процесса очистки топочных газов от диоксида серы с использованием дистиллерной суспензии содового производства проводились на Стерлитамакском ОАО “Сода”. Очистке подвергался газ из печей огневых кальцинаторов соды. Дистиллерная суспензия подавалась из цеха абсорбции дистилляции - карбонизации (АДК).
Параметры газа:
o расход 30003500 м3/ч;
o избыточное давление 2,12,2 кПа;
o температура 170205 С
o скорость газа в свободном сечении аппарата 2,12,5 м/с;
o массовая концентрация SO2 670840 мг/м3;
o объемная доля СО2 6,88 %;
На орошение опытного газоочистного аппарата подавали дистиллерную суспензию со следующими параметрами:
o плотность орошения 3,34,7 кг/м2с;
o температура 8290 С;
o
рН 11,411,6.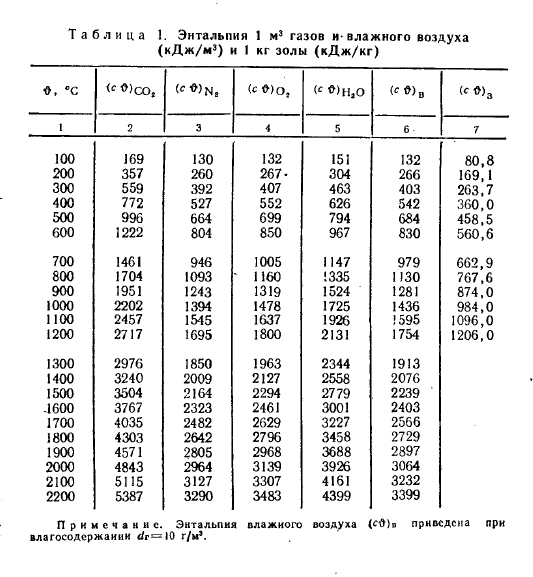
Опытный газоочистной аппарат был собран из чугунных царг диаметром 700 мм и имел общую высоту 11 м. В нем были установлены 5 контактных устройств (провальные дырчатые тарелки с диаметром отверстий 60 мм и долей свободного сечения 0,22 м2/м2). Под каждым контактным устройством располагался пробоотборник для жидкости, а над ним гильза термометра сопротивления, причем таким образом, чтобы она всегда была в слое жидкости. Имелась возможность замера гидравлического сопротивления каждого контактного устройства.
Средние значения параметров потоков на выходе из газоочистного аппарата в процессе испытаний были следующие.
Газ:
– температура 6772 С;
– вакуум 0,91,1 кПа;
– массовая концентрация SO2 3564 мг/м3;
– степень
очистки от SO2
92,394,8 %.
жидкость:
– температура 6165 С;
– рН 11,211,4.
Как видно из приведенных данных, на пилотном аппарате удалось достичь заданной нормами ПДВ степени очистки топочных газов от диоксида серы. Концентрация SO2 ни в одном замере не превышала 70 мг/м3, что соответствует требованиям санитарных служб.
Сравнение
результатов
лабораторных
опытов с
работой
пилотной
установки
выполнялось
следующим
образом.
Расчет по
формуле (5.11) для
усредненных
результатов
опытов дает
следующее
значение
коэффициента
массопередачи
по диоксиду
серы: kг
= 9,710-4
моль/м2сПа.
Для
сравнения
расчет по
формуле (5.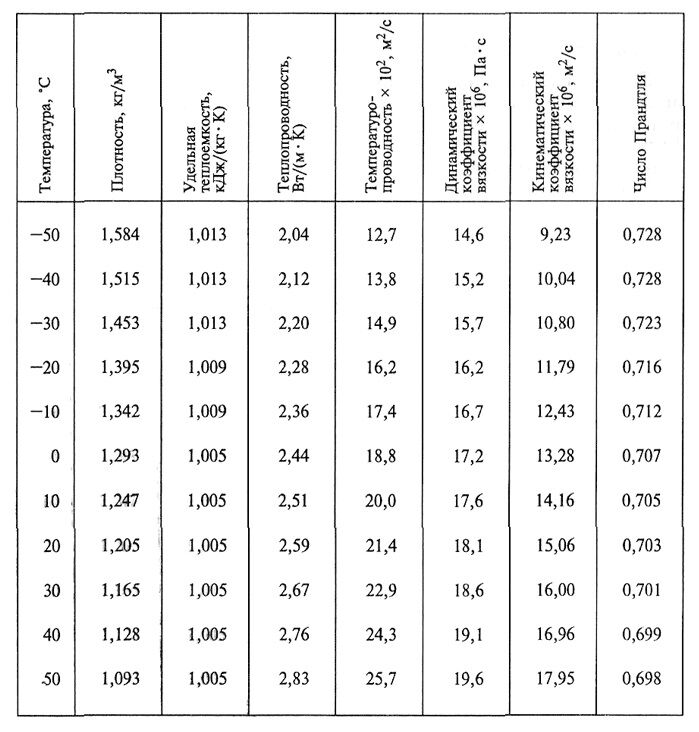 6) с
коэффициентами
из табл. 5.1,
полученными
в
лабораторных
опытах, дает
величину 14,110-4
моль/м2сПа.
Учитывая
особенности
исследуемой
системы (лимитирующая
стадия
процесса
растворение
гидроксида
кальция),
масштабный
переход, то
есть
увеличение
диаметра
пилотного
аппарата в
сравнении с
лабораторным
более чем в 20
раз, и
достаточно
далекую
экстраполяцию
данных
лабораторных
опытов, такое
совпадение
лабораторных
данных с
результатами
работы
опытного
аппарата
можно
считать
удовлетворительным.
Однако для
расчета
промышленного
аппарата
коэффициент а
из табл. 5.1
должен быть
скорректирован
с учетом
результатов
заводских
испытаний, то
есть
уменьшен в 1,5
раза.
6) с
коэффициентами
из табл. 5.1,
полученными
в
лабораторных
опытах, дает
величину 14,110-4
моль/м2сПа.
Учитывая
особенности
исследуемой
системы (лимитирующая
стадия
процесса
растворение
гидроксида
кальция),
масштабный
переход, то
есть
увеличение
диаметра
пилотного
аппарата в
сравнении с
лабораторным
более чем в 20
раз, и
достаточно
далекую
экстраполяцию
данных
лабораторных
опытов, такое
совпадение
лабораторных
данных с
результатами
работы
опытного
аппарата
можно
считать
удовлетворительным.
Однако для
расчета
промышленного
аппарата
коэффициент а
из табл. 5.1
должен быть
скорректирован
с учетом
результатов
заводских
испытаний, то
есть
уменьшен в 1,5
раза.
Опыты
на пилотном
аппарате
дали
материал для
проверки
методики
расчета
процесса
контактного
охлаждения
газов,
описанной в
разделе 5. 3.
Несколько
парадоксально
выглядит при
этом тот факт,
что и
дистиллерная
суспензия, и
топочный газ
в процессе
взаимодействия
в
газоочистном
аппарате
охлаждаются.
На самом деле
нарушения
закона
сохранения
энергии тут,
конечно же,
нет. Несмотря
на то, что
температура
выходящего
газа ниже, чем
входящего,
энтальпия
его выше за
счет
повышения
влагосодержания.
3.
Несколько
парадоксально
выглядит при
этом тот факт,
что и
дистиллерная
суспензия, и
топочный газ
в процессе
взаимодействия
в
газоочистном
аппарате
охлаждаются.
На самом деле
нарушения
закона
сохранения
энергии тут,
конечно же,
нет. Несмотря
на то, что
температура
выходящего
газа ниже, чем
входящего,
энтальпия
его выше за
счет
повышения
влагосодержания.
В табл. 5.5 сопоставлен расчёт температур жидкости на тарелках по алгоритму, описанному в подразделе 5.3, с результатами непосредственных замеров на опытном аппарате.
Расчет
выполнен для
усредненных
параметров
жидкости и
газа, имевших
место во
время
испытаний:
расход
дистиллерной
суспензии 4,7 м3/ч,
газа 3250 м3/час
и
температура
дистиллерной
суспензии 86 С,
газа 185 С.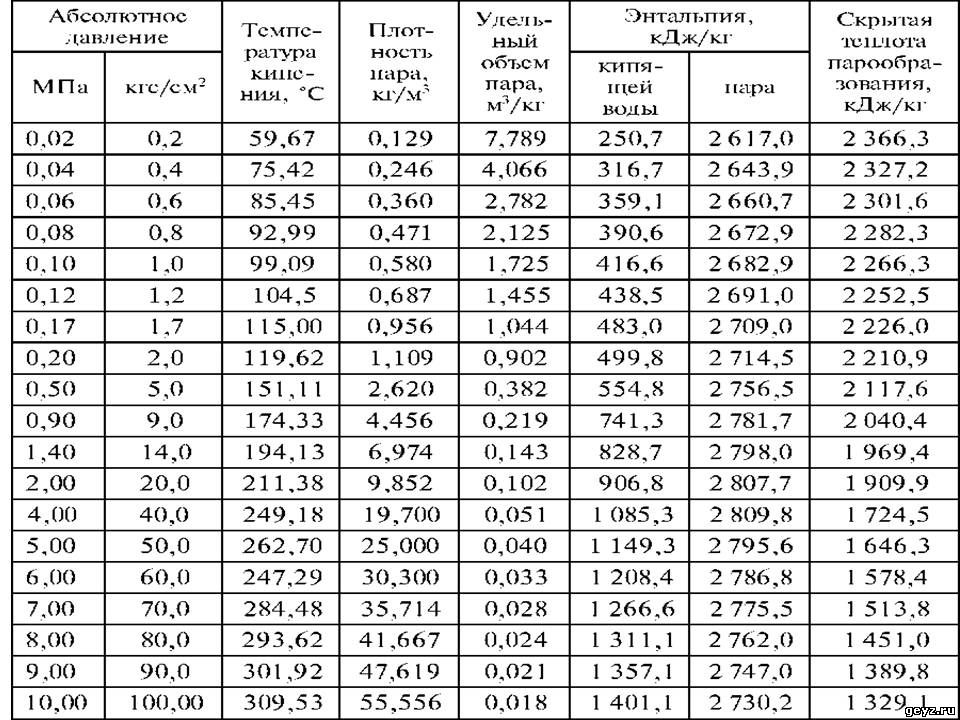
Таблица 5.5 Сравнение расчетных температур в пилотном аппарате с результатами замеров.
|
Номер тарелки |
Расчет |
Фактические замеры температуры, С |
||
|
Энтальпия газа, кДж/кг |
Влагосодержание, кг/кг сух. газа |
Температура жидкости, С |
||
|
1 |
315 |
0,099 |
57,7 |
60 |
|
2 |
330 |
0,104 |
59,4 |
62 |
|
3 |
353 |
0,112 |
61,9 |
64 |
|
4 |
392 |
0,126 |
66,3 |
67 |
|
5 |
471 |
0,154 |
74,9 |
72 |
|
Количество выпаренной воды |
304,6 кг/ч |
320 кг/ч |
||
Как видно из
табл. 5.5,
расчетные
температуры
отличаются
от
фактических
на величину
не более 2,5 С.
Совпадение
можно
считать
удовлетворительным,
так как при
замерах
температуры
усреднение
по площади
тарелки не
проводилось,
и отмеченные
отклонения
могут быть
результатом
неточности
замера.
Расчет
количества
выпаренной
из
дистиллерной
суспензии
воды также
совпал с
фактом с
точностью 5 %,
что для
инженерного
расчета
можно
считать
приемлемым.
Таким
образом,
можно
считать, что
предложенная
модель
процесса
контактного
охлаждения
газа
адекватна
эксперименту.
5.5,
расчетные
температуры
отличаются
от
фактических
на величину
не более 2,5 С.
Совпадение
можно
считать
удовлетворительным,
так как при
замерах
температуры
усреднение
по площади
тарелки не
проводилось,
и отмеченные
отклонения
могут быть
результатом
неточности
замера.
Расчет
количества
выпаренной
из
дистиллерной
суспензии
воды также
совпал с
фактом с
точностью 5 %,
что для
инженерного
расчета
можно
считать
приемлемым.
Таким
образом,
можно
считать, что
предложенная
модель
процесса
контактного
охлаждения
газа
адекватна
эксперименту.
Оценивая
конструктивные
характеристики
аппарата для
абсорбционной
очистки
топочных
газов от
диоксида
серы
дистиллерной
суспензией,
можно
отметить
следующее:
геометрические
размеры
контактного
элемента (диаметр
отверстий,
шаг, доля
свободного
сечения)
удовлетворяют
требованиям
ведения
процесса
абсорбции.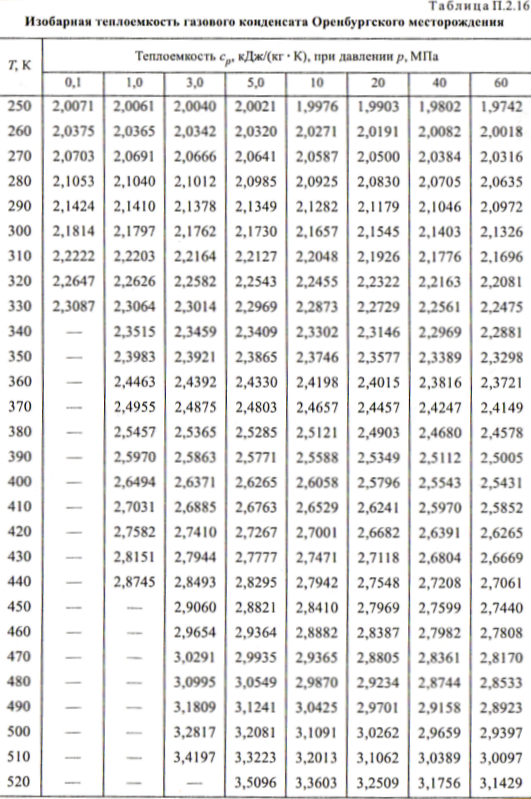 Выбранные
геометрические
размеры
тарелки
обеспечивают
хороший
контакт
между газом и
жидкостью, о
чем можно
судить по
степени
очистки газа.
Выбранные
геометрические
размеры
тарелки
обеспечивают
хороший
контакт
между газом и
жидкостью, о
чем можно
судить по
степени
очистки газа.
Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru – Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva. Поделиться:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вукалович М.П. Теплофизические свойства воды и водяного пара
Справочник
- формат djvu
- размер 4.21 МБ
- добавлен 28 сентября 2010 г.
М.: Машиностроение, 1967. – 160 с.
В книге приведены данные о теплофизических свойствах воды,
насыщенного и перегретого водяного пара в широкой области
параметров состояния до 1000 ат и 1000 градусов Цельсия и
диаграммы. Величины, приведенные в таблицах, получены на основании
обработки наиболее достоверного экспериментального материала и
полностью согласованы с Международными скелетными таблицами
термодинамических свойств воды и водяного пара.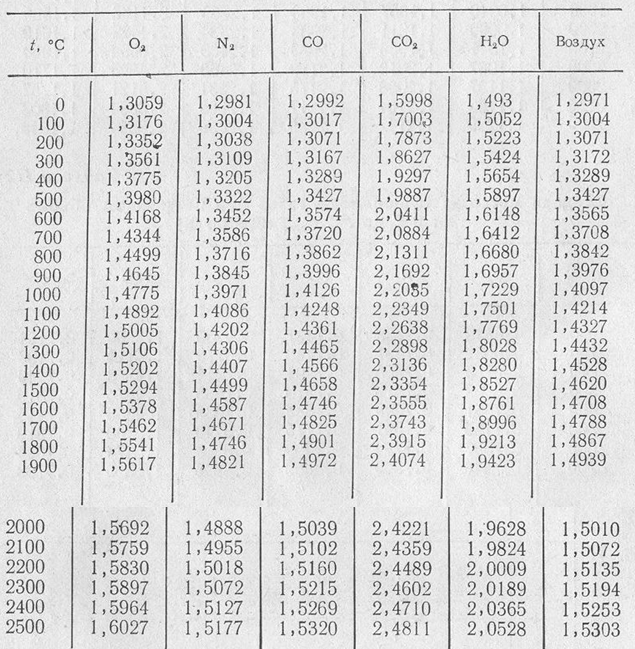 Все теплофизические
свойства водя и водяного пара приведены в двух системах единиц:
технической и СИ. Книга на русском, английском, французском и
испанском.
Все теплофизические
свойства водя и водяного пара приведены в двух системах единиц:
технической и СИ. Книга на русском, английском, французском и
испанском.
Смотрите также
- формат djvu
- размер 2.47 МБ
- добавлен 07 января 2009 г.
М.: Издательство МЭИ, 1999. – 168 с. Таблицы рассчитаны по уравнениям Международной ассоциации по свойствам воды и водяного пара и рекомендованы гос. службой стандартных справочных данных ГСССД Р-776-98. Приведены таблицы значений удельного объема, энтальпии, энтропии, изобарной теплоемкости, скорости звука, поверхностного натяжения, динамической вязкости, теплопроводности и числа Прандтля для воды и водяного пара, рассчитанных по уравнениям, р…
- формат djvu
- размер 1.77 МБ
- добавлен
04 июня 2009 г.
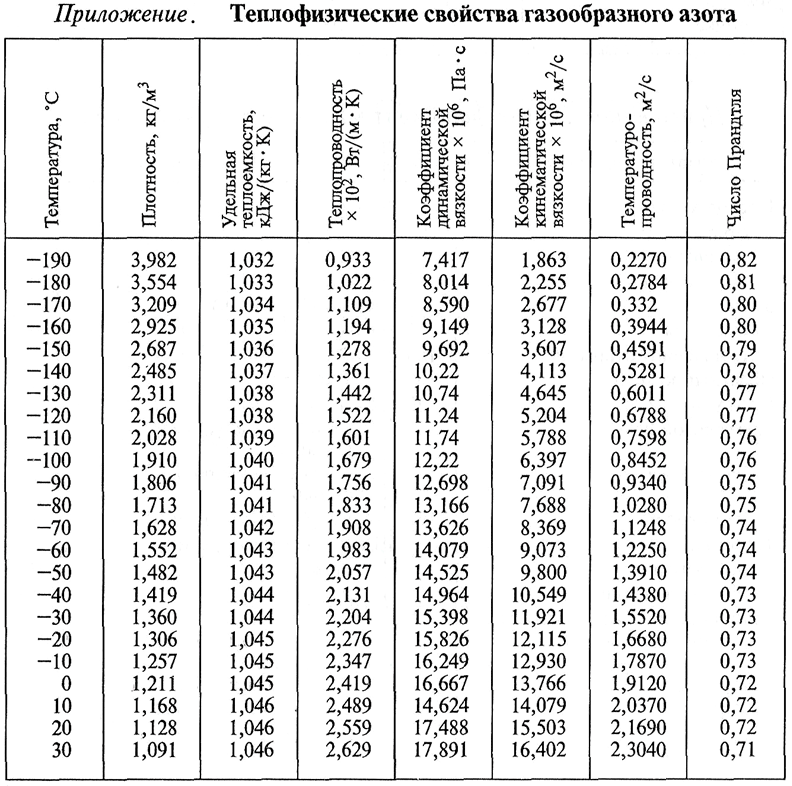
Учеб. пособие. – СПб.: СПбГАХПТ, 1998. – 146 с. В учебном пособии рассмотрены основные законы термодинамики идеальных газов и смесей, свойства сухого воздуха, водяного пара, воды и льда. Состав и свойства влажного воздуха ограничены диапазоном температур и давлений, характерных для процессов комфортного кондиционирования воздуха. Приведены данные по влиянию кривизны поверхности раздела фаз на давление насыщения, радиуса капли – на температуру…
- формат pdf
- размер 1.65 МБ
- добавлен 27 декабря 2010 г.
Учебное пособие составлено в соответствии с программой курса “Теплофизические свойства веществ” Государственного стандарта высшего и профессионального образования для направления подготовки дипломированных специалистов 651100 – Техническая физика, специальность 070700 – Теплофизика.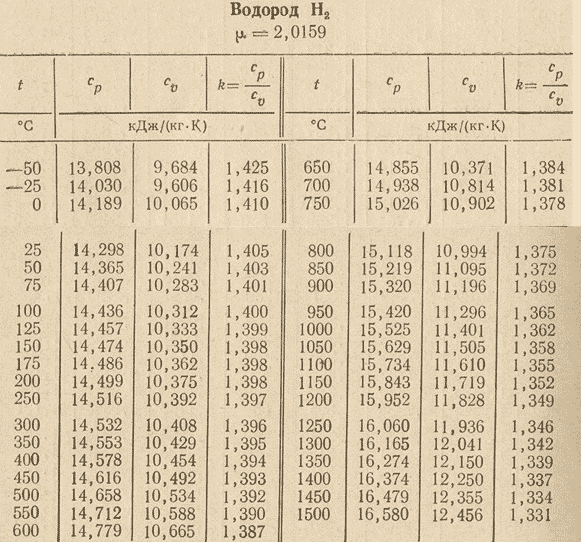 В настоящее учебное пособие вошли главы, посвященные исследованию теплофизических свойств газов и жидкостей. В каждой из глав даны краткие теоретические сведения и пр…
В настоящее учебное пособие вошли главы, посвященные исследованию теплофизических свойств газов и жидкостей. В каждой из глав даны краткие теоретические сведения и пр…
- формат gif
- размер 48.6 МБ
- добавлен 08 мая 2010 г.
1969-162 стр. В справочнике приведены данные о термодинамических свойствах и коэффициентах переноса воды и водяного пара, согласующиеся с международными скелетными таблицами, принятыми на VI международной конференции по свойствам водяного пара в 1963 г. Таблицы термодинамических свойств при давлениях до 1000 бар и температурах до 800С, включая состояние насыщения. Таблицы коэффициента динамической вязкости при давлениях до 800 бар и температурах…
- формат pdf
- размер 1.18 МБ
- добавлен 17 ноября 2010 г.
Для студентов всех видов обучения кафедры ТЭС и родственных.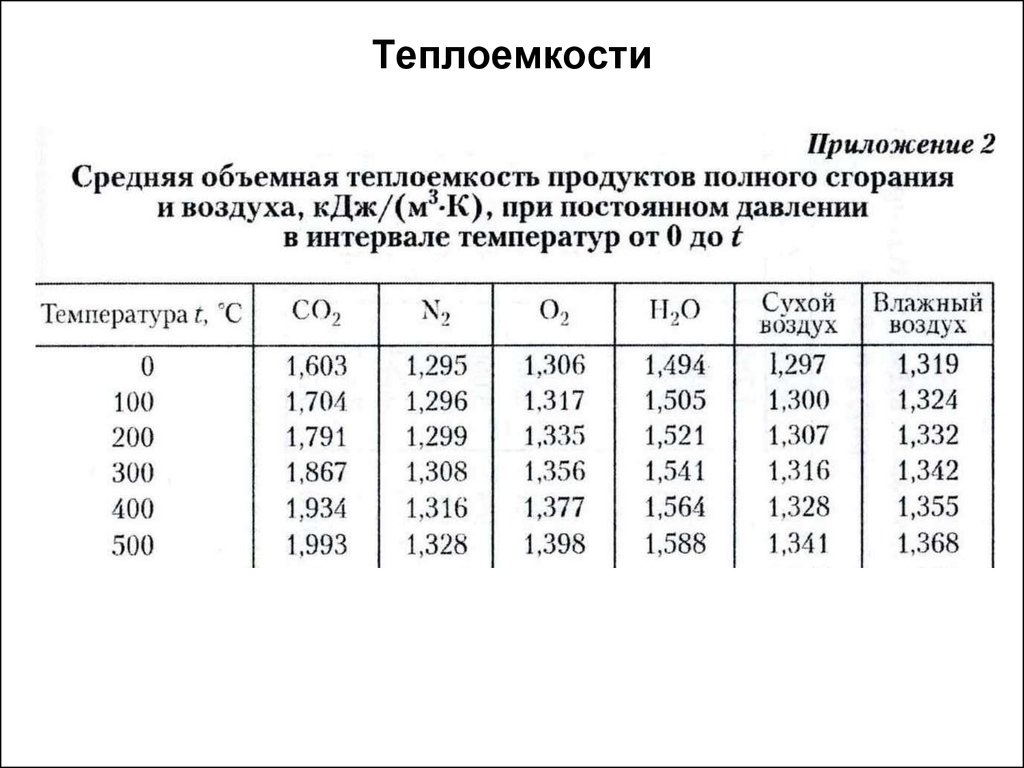 Сборник технических задач с решениями, в нем представлены 24 задачи по 6 разделам курса лекций. Задачи содержат 36 рисунков и 17 таблиц. В ходе решения задач используются термодинамические таблицы и диаграммы: воды и водяного пара, хладонов, воздуха и других газов, а также таблицы газодинамических функций. Эти материалы не даны в приложении к сборнику. Технические задачи, предлагаемые в…
Сборник технических задач с решениями, в нем представлены 24 задачи по 6 разделам курса лекций. Задачи содержат 36 рисунков и 17 таблиц. В ходе решения задач используются термодинамические таблицы и диаграммы: воды и водяного пара, хладонов, воздуха и других газов, а также таблицы газодинамических функций. Эти материалы не даны в приложении к сборнику. Технические задачи, предлагаемые в…
Презентация
- формат ppt
- размер 395 КБ
- добавлен 26 мая 2011 г.
Свойства пара
Справочник
- формат djvu
- размер 17.52 МБ
- добавлен
02 октября 2011 г.

– М.: Энергия, 1980. – 424 с., ил. Книга содержит табличные данные о термодинамических свойствах и коэффициентах переноса воды и водяного пара. Книга снабжена h, s-диаграммой водяного пара. Предлагаемые таблицы являются наиболее полными и точными из всех выпускавшихся в СССР. Книга предназначена для инженеров и научных работников – теплотехников и теплоэнергетиков Она рекомендована Учебно-методическим управлением по высшему образованию для исполь…
Практикум
- формат doc
- размер 1.61 МБ
- добавлен 08 октября 2011 г.
Ижевск, ФГОУ ВПО Ижевская ГСХА, 2009. – 108 с. Учебно-методическое пособие к лабораторным работам для студентов, обучающихся по направлению «Агроинженерия».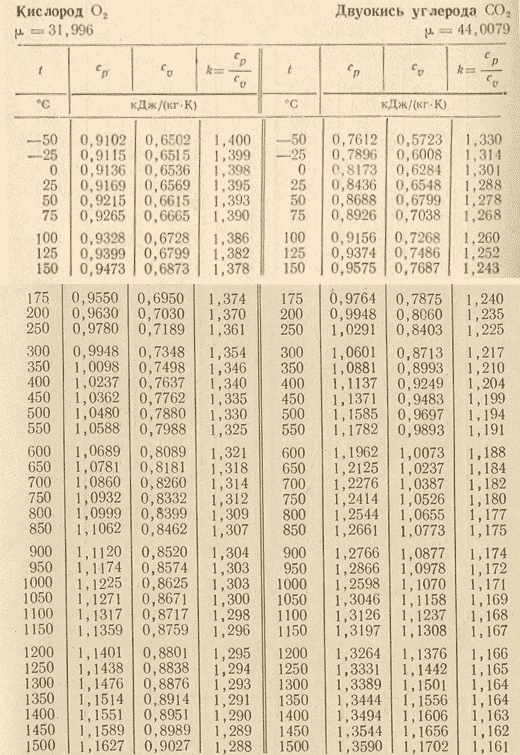 Исследование параметров воздуха с целью определения показателя адиабаты. Исследование зависимости давления водяного пара от температуры. Определение параметров влажного воздуха. Определение коэффициента теплопроводности методом цилиндра. Определение теплоемкости воздуха. Определение коэффицие…
Исследование параметров воздуха с целью определения показателя адиабаты. Исследование зависимости давления водяного пара от температуры. Определение параметров влажного воздуха. Определение коэффициента теплопроводности методом цилиндра. Определение теплоемкости воздуха. Определение коэффицие…
- формат xls
- размер 1.28 МБ
- добавлен 09 мая 2010 г.
Файл в формате .xls по известной температуре и давлению расчитывает плотность, удельный объем, энтальпию, энтропию, теплоемкость, теплопроводность, динамическую вязкость. Определяется агрегатное состояние воды. Для правильной работы необходимо, чтобы были включены макросы. Данные для расчета взяты из: Ривкин С. Л., Александров А. А. Термодинамические свойства воды и водяного пара, 1975
- формат txt, doc, pdf
- размер 1.87 МБ
- добавлен
26 декабря 2009 г.
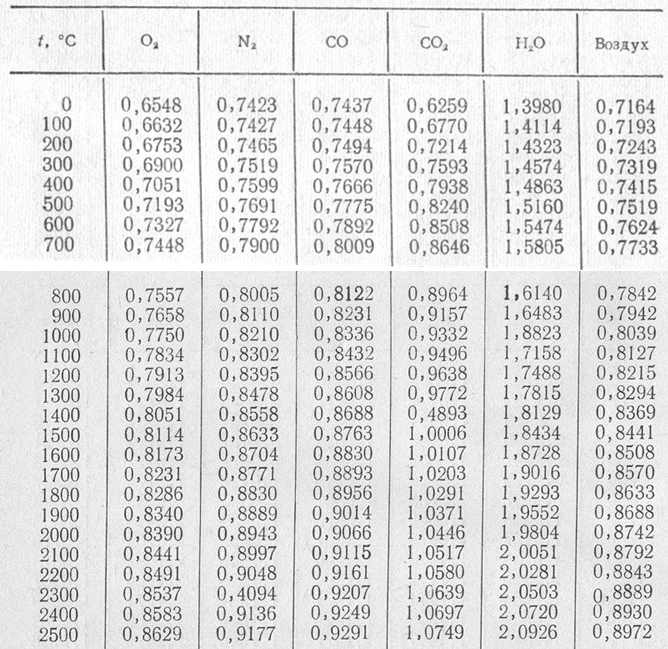
Электронный справочник «Теплофизические свойства теплоносителей» Позволяет выполнять расчет теплофизических свойств (удельного объема, энтальпии, энтропии, теплоемкости, коэффициента теплопроводности и т. д. ) различных теплоносителей, в частности: воды и водяного пара (IAPWS-IF97 formulations), воздуха и дымовых газов (нормативный метод). Дополнительно справочник оснащается соответствующей DLL-библиотекой для работы с компилятором Builder C++ 6….
Температура горения дров. Какие дрова лучше выбрать
Какая температура горения дров в печи – породы дерева, какие дрова лучше выбрать
Содержание:
Температурный порог горения древесины различных пород
Использование древесины исходя из ее теплоемкости
Теплоотдача при сгорании дров в печи
Что собой представляет процесс горения
Как определить температуру горения в печи на дровах
Жаропроизводительность древесины
Влажность и интенсивность горения
Как тяга в печке влияет на горение
Выводы
Видео
Дрова являются традиционным видом твердого топлива, которое издавна использовалось в регионах, где есть большое количество доступной древесины.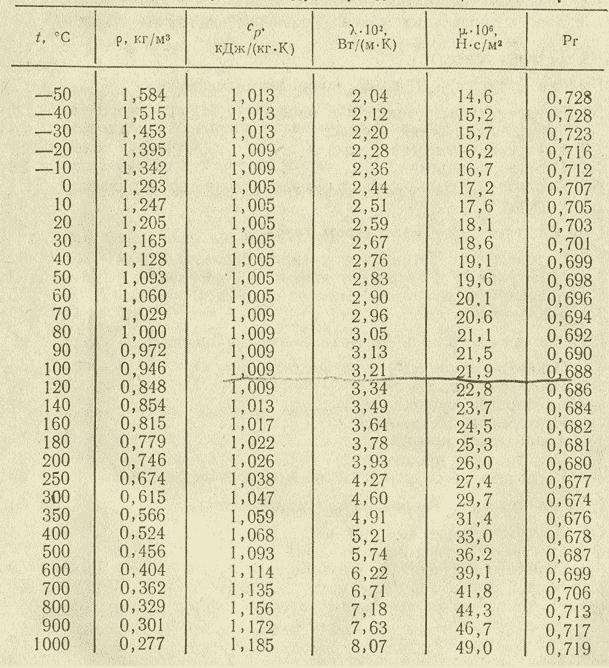 От того, насколько высока температура горения дров в печке, зависит не только скорость прогрева дома, но и эффективность применения топлива, а значит, и размер финансовых затрат. Об основных характеристиках древесины, а также факторах, влияющих на количество выделяемой дровами тепловой энергии, и пойдет речь в статье ниже.
От того, насколько высока температура горения дров в печке, зависит не только скорость прогрева дома, но и эффективность применения топлива, а значит, и размер финансовых затрат. Об основных характеристиках древесины, а также факторах, влияющих на количество выделяемой дровами тепловой энергии, и пойдет речь в статье ниже.
Температурный порог горения древесины различных пород
В зависимости от структуры и плотности древесины, а также количества и характеристик смол, зависит температура горения дров, их теплотворность, а также свойства пламени.
Если дерево пористое, то гореть оно будет очень ярко и интенсивно, однако высоких температур горения оно не даст – максимальный показатель составляет 500 ℃. А вот более плотная древесина, как, например, у граба, ясеня или бука, сгорает при температуре около 1000 ℃. Чуть ниже температура горения у березы (около 800 ℃), а также дуба и лиственницы (900 ℃). Если речь идет о таких породах, как ель и сосна, то они загораются примерно при 620-630 ℃.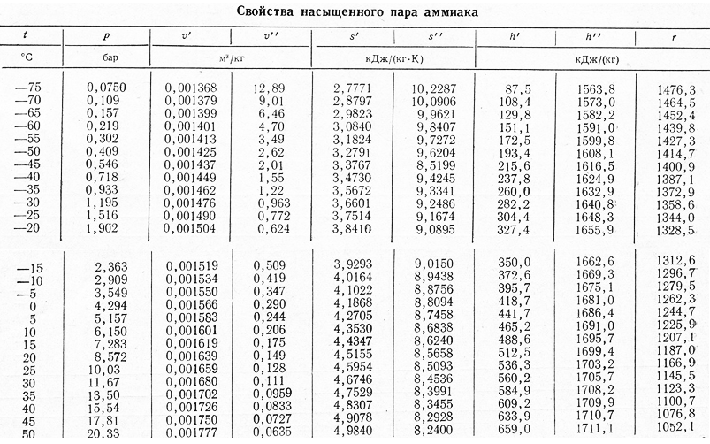
При выборе разновидности дров, стоит учитывать соотношение стоимости и теплоемкости той или иной древесины. Как показывает практика, оптимальным вариантом можно считать березовые дрова, у которых эти показатели сбалансированы лучше всего. Если закупать более дорогие дрова, затраты будут менее эффективными.
Для отопления дома твердотопливным котлом не рекомендуют использовать такие виды дерева, как ель, сосна или пихта. Дело в том, что в данном случае температура горения дров в котле будет недостаточно высокой, а на дымовых трубах будет скапливаться много сажи.
Низкие показатели теплоэффективности также и у дров из ольхи, осины, липы и тополя из-за пористой структуры. Кроме того, иногда в процессе горения ольховые и некоторые другие виды дров выстреливают углями. В случае открытой топки печи такие микро взрывы могут привести к пожарам.
Стоит отметить, что какой бы ни была древесина, если она сырая, то горит хуже сухой и сгорает не до конца, оставляя много золы.
Теплоотдача при сгорании дров в печи
Существует прямая взаимосвязь между температурой горения дров в печи и теплоотдачей – чем жарче пламя, тем больше тепла оно выделяет в помещение. На количество генерируемой тепловой энергии влияют различные характеристики дерева. Расчетные величины можно найти в справочной литературе.
Стоит отметить, что все нормативные показатели рассчитывались в идеальных условиях:
- древесина хорошо просушена;
- топка печи закрыта;
- кислород подается четко дозированными порциями для поддержания процесса горения.
Естественно, что в домашней печи создать такие условия невозможно, поэтому тепла будет выделяться меньше, чем показывают расчеты. Поэтому нормативы будут полезны лишь для определения общей динамики и сравнения характеристик.
Что собой представляет процесс горения
Изотермическая реакция, при которой выделяется определенное количество тепловой энергии и называется горением. Эта реакция проходит несколько последовательных стадий.
Эта реакция проходит несколько последовательных стадий.
На первом этапе древесина разогревается внешним источником огня до точки воспламенения. По мере нагрева до 120-150 ℃ древесина превращается в угли, которая способна самовоспламеняться. По достижении температуры в 250-350 ℃ начинают выделяться горючие газы – этот процесс называется пиролизом. Одновременно происходит тление верхнего слоя древесины, которое сопровождается белым или бурым дымом – это смешанные пиролизные газы с водяным паром.
На втором этапе в результате разогрева пиролизные газы загораются светло-желтым пламенем. Оно постепенно распространяется на всю площадь древесины, продолжая нагрев древесины.
Следующая стадия характеризуется воспламенением древесины. Как правило, для этого она должна разогреться до 450-620 ℃. Чтобы дрова воспламенились, необходим внешний источник тепла, который будет достаточно интенсивным для резкого нагрева дерева и ускорения реакции.
Кроме того, на скорость воспламенения дров влияют такие факторы, как:
- тяга;
- влажность древесины;
- сечение и форма дров, а также их количество в одной закладке;
- структура древесины – рыхлые дрова загораются быстрее, чем плотные;
- размещение дерева относительно потока воздуха – горизонтально или вертикально.

Проясним некоторые моменты. Поскольку влажное дерево при горении в первую очередь испаряет лишнюю жидкость, то разжигается и сгорает оно намного хуже, чем сухое. Форма также имеет значение – ребристые и зазубренные бревна воспламеняются легче и быстрее, чем гладкие и круглые.
Тяга в дымоходе должна быть достаточной, чтобы обеспечить приток кислорода и рассеять внутри топки тепловую энергию на все находящиеся в ней объекты, но не задуть при этом огонь.
Четвертая стадия термохимической реакции – устойчивый процесс горения, который после вспышки пиролизных газов охватывает все находящееся в топке топливо. Горение проходит две фазы – тление и горение пламенем.
В процессе тления сгорает образовавшийся в результате пиролиза уголь, при этом газы выделяются довольно медленно и не могут воспламениться по причине малой концентрации. В результате конденсирования газов по мере их охлаждения образуется белый дым. Когда древесина тлеет, внутрь постепенно проникает свежий кислород, что приводит к дальнейшему распространению реакции на все остальное топливо. Пламя возникает в результате сгорания пиролизных газов, которые перемещаются вертикально по направлению к выходу.
Пламя возникает в результате сгорания пиролизных газов, которые перемещаются вертикально по направлению к выходу.
Пока внутри печи поддерживается необходимая температура, подается кислород и есть не сгоревшее топливо, процесс горения продолжается.
Если такие условия не поддерживаются, то термохимическая реакция переходит в финальную стадию – затухание.
Как определить температуру горения в печи на дровах
Измерение температуры горения дров в камине можно выполнять только пирометром – никакие другие измерительные приборы для этого не годятся.
Если же такого прибора у вас нет, можно визуального определить примерные показатели, исходя из цвета пламени. Так, пламя низкой температуры имеет темно-красную окраску. Желтый огонь свидетельствует о слишком высокой температуре, получаемой с помощью усиления тяги, однако в этом случае большее количество тепла сразу улетучивается сквозь дымовую трубу. Для печи или камина наиболее подходящей будет температура горения, при которой цвет пламени будет желтым, как, например, у сухих березовых дров.
Современные печи и твердотопливные котлы, а также камины закрытого типа, оборудованы системой контроля подачи воздуха, чтобы корректировать теплоотдачу и интенсивность горения.
Жаропроизводительность древесины
Помимо значения теплотворности, то есть количества выделяемой тепловой энергии при сгорании топлива, есть еще понятие жаропроизводительности. Это та максимальная температура в печи на дровах, которой может достигать пламя в момент интенсивного горения древесины. Данный показатель также полностью зависит от характеристик древесины.
В частности, если дерево имеет рыхлую и пористую структуру, оно сгорает на довольно низких температурах, образуя светлое высокое пламя, и дает довольно мало тепла. А вот плотная древесина, хоть и гораздо хуже разгорается, даже при слабом и низком пламени дает высокую температуру и большое количество тепловой энергии.
Влажность и интенсивность горения
Если древесина была срублена недавно, то в ней содержится от 45 до 65 % влаги в зависимости от времени года и породы. У таких сырых дров температура горения в камине будет невысокой, поскольку большое количество энергии будет затрачиваться на испарение воды. Следовательно, теплоотдача от сырых дров будет достаточно низкой.
У таких сырых дров температура горения в камине будет невысокой, поскольку большое количество энергии будет затрачиваться на испарение воды. Следовательно, теплоотдача от сырых дров будет достаточно низкой.
Достигнуть оптимальных показателей температуры в камине и выделения достаточного для прогрева количества тепловой энергии можно несколькими способами:
- Сжигать за один раз в 2 раза больше топлива, чтобы обогреть дом или приготовить еду. Такой подход чреват существенными материальными затратами и усиленным накоплением сажи и конденсата на стенках дымоотвода и в ходах.
- Сырые бревна распиливают, колют на небольшие поленья и размещаются под навесом для просушки. Как правило, за 1-1,5 года дрова теряют до 20 % влаги.
- Дрова можно закупить уже хорошо просушенными. Хотя они несколько дороже, зато теплоотдача от них намного больше.
Стоит отметить, что совершенно непригодна для использования в качестве топлива древесина сырого срубленного тополя и некоторых других пород.
Она рыхлая, содержит очень много воды, поэтому при горении дает очень мало тепла.
В то же время, у березовых сырых дров наблюдается достаточно высокая теплотворность. Кроме того, пригодны для использования сырые поленья из граба, ясеня и прочих пород дерева с плотной древесиной.
Как тяга в печке влияет на горение
Если в топку печи поступает недостаточное количество кислорода, то интенсивность и температура горения древесины снижается, а вместе с тем сокращается и ее теплоотдача. Некоторые предпочитают прикрывать поддувало в печке, чтобы продлить время горения одной закладки, однако в результате топливо сгорает с более низким КПД.
Если дрова сжигают в открытом камине, то в таком случае кислород свободно поступает в топку. В данном случае тяга зависит главным образом от характеристик дымовой трубы.
В идеальных условиях формула термохимической реакции выглядит примерно так:
C+2H2+2O2=CO2+2H2O+Q (тепловая энергия).
Это значит, что при доступе кислорода происходит сгорание водорода и углерода, что в результате дает тепловую энергию, водяной пар и углекислый газ.
Для максимальной температуры сгорания сухого топлива в топку должно поступать около 130 % кислорода, необходимого для горения. Когда входные заслонки перекрывают, образуется избыток угарных газов, вызванных недостатком кислорода. Такой недожженный углерод улетучивается в дымоход, однако внутри топки падает температура горения и сокращается теплоотдача топлива.
Современные твердотопливные котлы очень часто оборудованы специальными теплоаккумуляторами. Эти устройства накапливают излишнее количество тепловой энергии, выделяемой в процессе горения топлива при условии хорошей тяги и с высоким КПД. Таким способом можно экономить топливо.
В случае с печами на дровах возможностей экономить дрова не так уж и много, поскольку они сразу же отдают тепло в воздух. Сама печка способна сохранять лишь небольшое количество тепла, а вот железная печь и вовсе на такое не способна – из нее лишнее тепло сразу же уходит в трубу.
Так, при увеличении тяги в печи можно добиться усиления интенсивности горения топлива и его теплоотдачи. Однако в таком случае существенно возрастают теплопотери. Если же обеспечить медленное сгорание дров в печи, то их теплоотдача будет меньше, а количество угарного газа – больше.
Обратите внимание, что КПД теплогенератора напрямую влияет на эффективность сжигания дров. Так, твердотопливный котел может похвастаться 80 % эффективности, а печь – всего 40 %, причем имеет значение ее конструкция и материал.
Выводы
Таким образом, наилучшим вариантом с точки зрения экономии средств, а также эффективности сгорания и теплоотдачи, можно считать дрова из березы. Поскольку твердые породы древесины с высокой жаропроизводительностью стоят существенно дороже, они используются в качестве дров намного реже.
Удельная теплоемкость воздуха
Удельная теплоемкость воздуха – (обновлено 26. 07.08)
07.08)Номинальные значения, используемые для воздуха при температуре 300 K: C P = 1,00 кДж/кг.K, C v = 0,718 кДж/кг·К, а к = 1,4. Однако все они являются функциями температуры, а также с чрезвычайно высоким температурным диапазоном опыт работы с двигателями внутреннего сгорания и газотурбинными двигателями получить существенные ошибки. В следующей таблице приведены значения удельная теплоемкость в зависимости от температуры. Мы находим, что выбор значений удельных теплоемкостей в среднем температура каждого процесса дает результаты с достаточной точностью (в пределах 1%).
Идеальный газ удельная теплоемкость воздуха
Температура
КC P
кДж/кг.KC v
кДж/кг.Kк
250
1,003
0,716
1,401
300
1,005
0,718
1.
 400
400350
1,008
0,721
1,398
400
1,013
0,726
1,395
450
1,020
0,733
1,391
500
1,029
0,742
1,387
550
1,040
0,753
1,381
600
1,051
0,764
1,376
650
1,063
0,776
1,370
700
1,075
0,788
1,364
750
1,087
0,800
1,359
800
1,099
0,812
1,354
900
1.
 121
1210,834
1,344
1000
1,142
0,855
1,336
1100
1,155
0,868
1,331
1200
1,173
0,886
1,324
1300
1.190
0,903
1,318
1400
1.
 204
2040,917
1,313
1500
1,216
0,929
1,309
Значения до 1000 К первоначально были опубликованы в “Таблицах тепловых свойств газов», NBS Circular 564, 1955. Последний пять строк были рассчитаны по формуле BG Kyle “Chemical и термодинамика процессов», Englewood Cliffs / Prentice Hall, 1984 г. и имеют погрешность <1%.
__________________________________________________________________________________________
Инженерная термодинамика Израиля
Уриэли находится под лицензией Creative
Commons Attribution-Noncommercial-Share Alike 3.0 США
Лицензия
Удельная теплоемкость и индивидуальные газовые постоянные
Удельная теплоемкость (= удельная теплоемкость) при процессах с постоянным давлением и постоянным объемом, а также отношение удельных теплоемкостей и индивидуальных газовых постоянных – R – для некоторых широко используемых “идеальных газов” , приведены в таблице ниже (приблизительные значения для 68 o F ( 20 o C ) и 14,7 фунтов на кв. дюйм ( 1 атм )).
дюйм ( 1 атм )).
Для перевода единиц измерения используйте онлайн-конвертер единиц Удельная теплоемкость.
См. также табличные значения удельной теплоемкости пищевых продуктов и пищевых продуктов, металлов и полуметаллов, обычных жидкостей и жидкостей, обычных твердых и других обычных веществ, а также значения молярной теплоемкости обычных органических веществ и неорганических веществ.
Для полной таблицы – повернуть экран!
| Газ или пар | Формула | Удельная теплоемкость | Коэффициент удельной теплоемкости | Individual Gas constant – R – | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| c p (kJ/(kg K)) | c v (kJ /(kg K)) | c p (Btu/(lb m o F)) | c v (BTU / (LB M O F)) | κ = C P / C V | C | C | C | C | C | . (kJ/(kg K)) (kJ/(kg K)) | c p – c v (ft lb f /(lb m o R)) | ||||||
| Ацетон | (CH 3 ) 2 CO | 1.47 | 1.32 | 0.35 | 0.32 | 1.11 | 0.15 | ||||||||||
| Acetylene | C 2 H 2 | 1.69 | 1.37 | 0.35 | 0.27 | 1.232 | 0.319 | 59.34 | |||||||||
| Air | 1.01 | 0.718 | 0.24 | 0.17 | 1.40 | 0.287 | 53.34 | ||||||||||
| Alcohol (ethanol) | C 2 H 5 OH | 1.88 | 1.67 | 0.45 | 0.4 | 1.13 | 0. 22 22 | ||||||||||
| Alcohol ( Метанол) | CH 3 OH | 1,93 | 1,53 | 0,46 | 0,37 | 1,26 | 0,39 | ||||||||||
| . 0,39 | |||||||||||||||||
| .My0553 NH 3 | 2.19 | 1.66 | 0.52 | 0.4 | 1.31 | 0.53 | 96.5 | ||||||||||
| Argon | Ar | 0.520 | 0.312 | 0.12 | 0.07 | 1.667 | 0,208 | ||||||||||
| Бензол | C 6 H 6 | 1,09 | 0,99 | 0,26 | 0,24 | 1.12 | 0,26 | 0,24 | 1,1129.12 | 0,26 | 0,24 | 0,26 | 0,24 | 505020202020500200.1 | |||
| Blast furnace gas | 1.03 | 0.73 | 0.25 | 0. 17 17 | 1.41 | 0.3 | 55.05 | ||||||||||
| Bromine | Br 2 | 0.25 | 0.2 | 0,06 | 0,05 | 1,28 | 0,05 | ||||||||||
| Бутан | C 4 H 10 0004 | 1,67 40004 H 100004 | 1,67 0020 | 1.53 | 0.395 | 0.356 | 1.094 | 0.143 | 26.5 | ||||||||
| Carbon dioxide | CO 2 | 0.844 | 0.655 | 0.21 | 0.16 | 1.289 | 0.189 | 38,86 | |||||||||
| Углеродного моноксида | CO | 1,02 | 0,72 | 0,24 | 0,17 | 1,40 | 0,2957 | 55.14 | |||||||||
| Carbon disulphide | CS 2 | 0.67 | 0.55 | 0.16 | 0.13 | 1. 21 21 | 0.12 | ||||||||||
| Chlorine | Cl 2 | 0.48 | 0,36 | 0,12 | 0,09 | 1,34 | 0,12 | ||||||||||
| Хлороформ | CHCL 3 | 0303 | CHCL 3 | 0.63 | 3 | 03 9003 | 3 | 03 9003 | CHCL 3 | 9053 0.63 90033 | 9053 0.63 9003CHCL 3 | 9053 0.00200.55 | 0.15 | 0.13 | 1.15 | 0.08 | |
| Coal gas | 2.14 | 1.59 | |||||||||||||||
| Combustion products | 1 | 0.24 | |||||||||||||||
| Этан | C 2 H 6 | 1,75 | 1,48 | 9 035530553 0.321.187 | 0. 276 276 | 51.5 | |||||||||||
| Ether (diethyl ether) | (C 2 H 5 ) 2 O | 2.01 | 1.95 | 0.48 | 0.47 | 1.03 | 0.06 | ||||||||||
| Ethylene | C 2 H 4 | 1.53 | 1.23 | 0.4 | 0.33 | 1.240 | 0.296 | 55.08 | |||||||||
| Chlorodifluoromethane, R-22 | CHClF 2 | 1.18 | |||||||||||||||
| Helium | He | 5.19 | 3.12 | 1,25 | 0,75 | 1,667 | 2,08 | 386,3 | |||||||||
| Гексан | C 6 H 14 9000 | C 0020| | | | | 1. |  06 06 | | | ||||||||
| Hydrochloric acid | 0.795 | 0.567 | |||||||||||||||
| Hydrogen | H 2 | 14.32 | 10.16 | 3.42 | 2.43 | 1.405 | 4.12 | 765.9 | |||||||||
| Хлороводород | HCl | 0.8 | 0.57 | 0.191 | 0.135 | 1.41 | 0.23 | 42.4 | |||||||||
| Hydrogen Sulfide | H 2 S | 0.243 | 0.187 | 1.32 | 45,2 | ||||||||||||
| Hydroxyl | OH | 1,76 | 1,27 | 1,384 | 0,489 | 9 93840,489 | 9.0020|||||||||||
| Krypton | Kr | 0.25 | 0.151 | ||||||||||||||
| Methane | CH 4 | 2. 22 22 | 1.70 | 0.59 | 0.45 | 1.304 | 0.518 | 96.4 | |||||||||
| Метилхлорид | CH 3 Cl | 0,240 | 0,200 | 7 905 59 020 0,200553 30.6||||||||||||||
| Natural Gas | 2.34 | 1.85 | 0.56 | 0.44 | 1.27 | 0.5 | 79.1 | ||||||||||
| Neon | Ne | 1.03 | 0.618 | 1.667 | 0.412 | ||||||||||||
| Nitric Oxide | NO | 0.995 | 0.718 | 0.23 | 0.17 | 1.386 | 0.277 | ||||||||||
| Nitrogen | N 2 | 1.04 | 0.743 | 0.25 | 0.18 | 1.400 | 0.297 | 54.99 | |||||||||
| Nitrogen tetroxide | N 2 O 4 | 4. 69 69 | 4,6 | 1,12 | 1,1 | 1,02 | 0,09 | ||||||||||
| . NITROUS OXIDE | |||||||||||||||||
| 3.0020 | N 2 O | 0.88 | 0.69 | 0.21 | 0.17 | 1.27 | 0.18 | 35.1 | |||||||||
| Oxygen | O 2 | 0.919 | 0.659 | 0.22 | 0.16 | 1.395 | 0.260 | 48.24 | |||||||||
| Pentane | C 5 H 12 | 1.07 | |||||||||||||||
| Propane | C 3 H 8 | 1.67 | 1.48 | 0.39 | 0.34 | 1.13 | 0.189 | 35.0 | |||||||||
| Propene (Пропилен) | C 3 H 6 | 1,5 | 1,31 | 0,36 | 0,31 | 1,15 | 0,18 | 36,8 | 0,18 | 36,8 | 0,18 | 9053 36,80,18 | 36,8 | 0,18 | 36,8 9. 15 15 | 0,18 | 36,8 9.150020 |
| Водяной пар Пар 1 фунт на кв. дюйм абс. 120 – 600 o F | H 2 O | 1.93 | 1.46 | 0.46 | 0.35 | 1.32 | 0.462 | ||||||||||
| Steam 14.7 psia. 220 – 600 o F | H 2 O | 1,97 | 1,5 | 0,47 | 0,36 | 1,31 | 0,46 | 1,31 | 0,46 | 1,31 | 0,46 | . 360 – 600 o F | H 2 O | 2.26 | 1.76 | 0.54 | 0.42 | 1.28 | 0.5 |
| Sulfur dioxide (Sulphur dioxide) | SO 2 | 0.64 | 0.51 | 0.15 | 0.12 | 1.29 | 0.13 | 24.1 | |||||||||
| Xenon | Xe | 0. 16 16 | 0.097 | ||||||||||||||
- κ = C P / C V – Определенный уровень теплоемкости
- – Определенный уровень тепла
- – Определенный уровень тепла
– Определенный уровень теплоемности
– Определенный уровень тепла
. c v = удельная теплоемкость в процессе постоянного объема
- R- Индивидуальная газовая постоянная
Для перевода единиц используйте онлайн-конвертер единиц Удельная теплоемкость.
См. также табличные значения удельной теплоемкости пищевых продуктов и пищевых продуктов, металлов и полуметаллов, обычных жидкостей и жидкостей, обычных твердых тел и других обычных веществ, а также значения молярной теплоемкости обычных органических веществ и неорганических веществ.
Температура дымовых газов и тепло в потоке дымовых газов (БТЕ/час)
[ вернуться к полному списку компьютерных программ ] Эта компьютерная программа рассчитывает удельную теплоемкость (БТЕ/фунт-Ф) и энтальпию (БТЕ/фунт) для
типичные газы, содержащиеся в дымовых газах систем сжигания. Например, если вы просто вводите
предполагаемая температура дымовых газов программа рассчитает удельную теплоемкость и энтальпию каждого
компонентный газ в программе. Если вам нужна дополнительная информация, вы также можете ввести массовые потоки (фунты/час) каждого компонента газа, обнаруженного в дымовых газах (из анализа горения или
из полевых испытаний дымовых газов), и программа рассчитает расход энергии (БТЕ/час)
для каждого газа, а затем рассчитайте общее количество дымовых газов (БТЕ/ч), которое теряется при
расход дымовых газов.
Например, если вы просто вводите
предполагаемая температура дымовых газов программа рассчитает удельную теплоемкость и энтальпию каждого
компонентный газ в программе. Если вам нужна дополнительная информация, вы также можете ввести массовые потоки (фунты/час) каждого компонента газа, обнаруженного в дымовых газах (из анализа горения или
из полевых испытаний дымовых газов), и программа рассчитает расход энергии (БТЕ/час)
для каждого газа, а затем рассчитайте общее количество дымовых газов (БТЕ/ч), которое теряется при
расход дымовых газов.
Пример № 1. Определение температуры дымовых газов из печи, работающей на природном газе
В этом конкретном примере устройство сгорания представляет собой более старую модель с низким КПД, работающую на природном газе. Домашняя печь. Топливом считается стандартный природный газ (1040 БТЕ/станд. фут3), потребление топлива составляет 100 000 БТЕ/ч (основа высокой теплоты), а тепло, подаваемое в дом, составляет 80 000 БТЕ/ч. Процент избытка воздуха для этой системы сгорания составляет 10 %. Воздух для горения всасывается
из дома при 70 F и относительной влажности 35%. Из ручного расчета анализа сгорания (или из программы NGBULT77) вы можете определить объем сгорания
воздуха, поступающего в топку (массовый расход или ACFM) и массовый расход компонентов дымовых газов, которые
идут вверх по стеку. Ниже вы увидите эти данные вместе с общим объемом дымовых газов (БТЕ/час).
вверх по стеку:
Воздух для горения всасывается
из дома при 70 F и относительной влажности 35%. Из ручного расчета анализа сгорания (или из программы NGBULT77) вы можете определить объем сгорания
воздуха, поступающего в топку (массовый расход или ACFM) и массовый расход компонентов дымовых газов, которые
идут вверх по стеку. Ниже вы увидите эти данные вместе с общим объемом дымовых газов (БТЕ/час).
вверх по стеку:A. Энергозатраты печи
1. Потребляемое топливо: 100 000,00 БТЕ/час
2. Воздух для горения в печи: 1 194,31 БТЕ/час (17,8468 куб.
B. Рекуперация тепла
1. Рекуперация тепла (или доставка в дом): 80 000 БТЕ/час
C. Теплота дымовых газов
1. Теплота дымовых газов = 101 194,31 – 80 000
= 21 194,31 БТЕ/час
D. Составляющие газы в дымовых газах (по данным анализа сгорания или по результатам испытаний дымовой трубы)
| Массовый расход | Удельная теплоемкость | Энтальпия | Поток энергии | |
1. Двуокись углерода Двуокись углерода | 11,7888 фунтов/час | Неизвестно | Неизвестно | Неизвестно |
| 2. Азот | 61,0971 фунт/час | Неизвестно | Неизвестно | Неизвестно |
| 3. Кислород | 1,6725 фунта/час | Неизвестно | Неизвестно | Неизвестно |
4. SO2 SO2 | 0,0001 фунт/час | Неизвестно | Неизвестно | Неизвестно |
| 5. Аргон | 0,0934 фунта/час | Неизвестно | Неизвестно | Неизвестно |
| 6. Водяной пар | 9,6800 фунтов/час | Неизвестно | Неизвестно | Неизвестно |
7. Всего дымовых газов Всего дымовых газов | 84,3318 фунтов/час | Неизвестно | Неизвестно | 21 194,31 БТЕ/час |
E. Определение температуры дымовых газов с помощью CPGASH56
В этом случае температуру дымовых газов можно определить с помощью итеративного процесса ввод массовых потоков дымовых газов и предполагаемой температуры дымовых газов, чтобы увидеть, Общее количество дымовых газов БТЕ/час равно 21,194,31 БТЕ/час, если нет, попробуйте другой предполагаемая температура.
CPGASH.txt
CPGASH56.txt
Образец полного энергетического анализа малоэффективной печи с искусственной тягой на природном газе
Вытяжная печь на природном газе (PDF)Альтернативный подход, используемый для определения температуры дымовых газов при сжигании природного газа
Существует еще один подход, который можно использовать для определения температуры дымовых газов по печь на природном газе. На прилагаемой диаграмме используются процент избытка воздуха и процент
Доступное тепло (это процент поставляемой входной энергии).
На прилагаемой диаграмме используются процент избытка воздуха и процент
Доступное тепло (это процент поставляемой входной энергии).1. Процент избыточного воздуха: от 0 % до 1000 % (при температуре воздуха для горения 60 F)
2. Процент доступного тепла =
Общее количество подаваемого тепла (БТЕ/час) x 100
Общее количество тепла, поступающего в печь (БТЕ/час)
Для этого конкретного случая вы вводите диаграмму со следующими данными:
Процент избыточного воздуха = 10,00 %
Процент доступного тепла =
80 000 БТЕ/ч поставленного тепла x 100
(100 000 + 1194,31 БТЕ/ч)0007
= 79,06%
Таблица значений температуры дымовых газов = 520 F
Иллюстрация температуры дымовых газов (PDF)
[ вернуться к полному списку компьютерных программ ] [ вернуться к началу ]
Таблица общего коэффициента теплопередачи Графики и уравнение
Таблица общего коэффициента теплопередачи Диаграммы и уравнения
Каталог термодинамики | Каталог теплопередачи
Таблица общего коэффициента теплопередачи Таблица:
Коэффициент теплопередачи – это коэффициент пропорциональности между тепловым потоком и термодинамической движущей силой потока тепла (т. е. разностью температур, ΔT):
е. разностью температур, ΔT):
h = q/(Ts – K)
где :
q: количество требуемого тепла (тепловой поток), Вт/м2 т. е. тепловая мощность на единицу площади, q = d\dot{Q}/dA
h: коэффициент теплопередачи, Вт/(м 2 K )
Ц =
Температура поверхности твердого тела
K =
Окружающая жидкость Температура
Он используется при расчете теплопередачи, как правило, путем конвекции или фазового перехода между жидкостью и твердым телом. Коэффициент теплопередачи имеет единицы СИ в ваттах на квадратный метр-кельвин: Вт/(м 2 К). Коэффициент теплопередачи обратно пропорционален теплоизоляции. Это используется для строительных материалов (значение R) и для изоляции одежды.
Связанные ресурсы:
- Общий коэффициент теплопередачи – теплопередача
- Общий коэффициент теплопередачи Термодинамика
- Уравнение конвекции и калькулятор конвективной теплопередачи
- Преобразование теплопроводности
- Теплопроводность газов
- Теплопроводность обычных металлов и сплавов
Таблица общего коэффициента теплопередачи Трубы и трубки
Типы | Применение | Общий коэффициент теплопередачи – U – | |
| Вт/(м 2 К) | БТЕ/(фут 2 o F ч) | ||
| Трубчатые, нагревательные или охлаждающие | Газ при атмосферном давлении внутри и снаружи труб | 5 – 35 | 1 – 6 |
| Газ высокого давления внутри и снаружи труб | 150 – 500 | 25 – 90 | |
| Жидкость снаружи (внутри) и газ при атмосферном давлении внутри (снаружи) труб | 15 – 70 | 3 – 15 | |
| Газ под высоким давлением внутри и жидкость снаружи труб | 200 – 400 | 35 – 70 | |
| Жидкости внутри и снаружи труб | 150 – 1200 | 25 – 200 | |
| Пар снаружи и жидкость внутри труб | 300 – 1200 | 50 – 200 | |
| Трубчатый, конденсационный | Пар снаружи и охлаждающая вода внутри труб | 1500 – 4000 | 250 – 700 |
| Органические пары или аммиак снаружи и охлаждающая вода внутри труб | 300 – 1200 | 50 – 200 | |
| Трубчатый, испарительный | пар снаружи и высоковязкая жидкость внутри труб, естественная циркуляция | 300 – 900 | 50 – 150 |
| пар снаружи и маловязкая жидкость внутри труб, естественная циркуляция | 600 – 1700 | 100 – 300 | |
| пар снаружи и жидкость внутри труб, принудительная циркуляция | 900 – 3000 | 150 – 500 | |
| Теплообменники с воздушным охлаждением | Охлаждение воды | 600 – 750 | 100 – 130 |
| Охлаждение жидких легких углеводородов | 400 – 550 | 70 – 95 | |
| Охлаждение смолы | 30 – 60 | 5 – 10 | |
| Охлаждение воздуха или дымовых газов | 60 – 180 | 10 – 30 | |
| Охлаждение углеводородного газа | 200 – 450 | 35 – 80 | |
| Конденсация пара низкого давления | 700 – 850 | 125 – 150 | |
| Конденсация органических паров | 350 – 500 | 65 – 90 | |
| Пластинчатый теплообменник | жидкость в жидкость | 1000 – 4000 | 150 – 700 |
| Спиральный теплообменник | жидкость в жидкость | 700 – 2500 | 125 – 500 |
| конденсация пара в жидкость | 900 – 3500 | 150 – 700 | |
Таблица общего коэффициента теплопередачи Теплообменники
Нагреватели (без фазового перехода) | ||
| Горячая жидкость | Холодная жидкость | Общий U (БТЕ/ч-фут 2 -F) |
| Пар | Воздух | 10 – 20 |
| Пар | Вода | 250 – 750 |
| Пар | Метанол | 200 – 700 |
| Пар | Аммиак | 200 – 700 |
| Пар | Водные растворы | 100 – 700 |
| Пар | Легкие углеводороды (вязкость < 0,5 сП) | 100 – 200 |
| Пар | Средние углеводороды (0,5 сП < вязкость < 1 сП) | 50 – 100 |
| Пар | Тяжелые углеводороды (вязкость > 1) | 6 – 60 |
| Пар | Газы | 5 – 50 |
| Даутерм | Газы | 4 – 40 |
| Даутерм | Тяжелые масла | 8 – 60 |
| Дымовой газ | Ароматические углеводороды и пар | 5 – 10 |
Таблица общего коэффициента теплопередачи Промышленные испарители
Испарители | ||
| Горячая жидкость | Холодная жидкость | Общий U (БТЕ/ч-фут 2 -F) |
| Пар | Вода | 350 – 750 |
| Пар | Органические растворители | 100 – 200 |
| Пар | Легкие нефтепродукты | 80 – 180 |
| Пар | Тяжелые масла (вакуум) | 25 – 75 |
| Вода | Хладагент | 75 – 150 |
| Органические растворители | Хладагент | 30 – 100 |
Таблица общего коэффициента теплопередачи Промышленные охладители
Охладители (без фазового перехода) | ||
| Холодная жидкость | Горячая жидкость | Общий U (БТЕ/час-фут 2 -F) |
| Вода | Вода | 150 – 300 |
| Вода | Органический растворитель | 50 – 150 |
| Вода | Газы | 3 – 50 |
| Вода | Легкие нефтепродукты | 60 – 160 |
| Вода | Тяжелые масла | 10 – 50 |
| Дизельное топливо | Органический растворитель | 20 – 70 |
| Рассол | Вода | 100 – 200 |
| Рассол | Органический растворитель | 30 – 90 |
| Рассол | Газы | 3 – 50 |
| Органические растворители | Органические растворители | 20 – 60 |
| Тяжелые масла | Тяжелые масла | 8 – 50 |
Таблица общего коэффициента теплопередачи Промышленные конденсаторы
Конденсаторы | ||
| Холодная жидкость | Горячая жидкость | Общий U (БТЕ/ч-фут 2 -F) |
| Вода | Пар (давление) | 350 -750 |
| Вода | Пар (вакуум) | 300 – 600 |
| Вода или рассол | Органический растворитель (насыщенный, атмосферный) | 100 – 200 |
| Вода или рассол | Органический растворитель (атмосферный, с высокой степенью неконденсации) | 20 – 80 |
| Вода или рассол | Органический растворитель (насыщенный, вакуум) | 50 – 120 |
| Вода или рассол | Органический растворитель (вакуум, высокая степень неконденсации) | 10 – 50 |
| Вода или рассол | Ароматические пары (атмосферные с неконденсируемыми газами) | 5 – 30 |
| Вода | Низкокипящий углеводород (атмосферный) | 80 – 200 |
| Вода | Высококипящий углеводород (вакуум) | 10 – 30 |
Таблица общего коэффициента теплопередачи Таблица различных жидкостей
без фазового перехода | |
| Жидкость | Коэффициент пленки (БТЕ/час-фут 2 -F) |
| Вода | 300 – 2000 |
| Газы | 3 – 50 |
| Органические растворители | 60 – 500 |
| Масла | 10 – 120 |
Таблица общего коэффициента теплопередачи. Таблица общего коэффициента теплопередачи Испарение Таблица общего коэффициента теплопередачи Различные жидкости (жидкости и газы) Зачем вам это Данные ввода/вывода Области, в которых эти расчеты полезны и для кого Эти данные полезны для инженеров-проектировщиков, инженеров-практиков котлов, консультантов и инженеров по эксплуатации котлов. Глубокое понимание термодинамики не является необходимым требованием для изучения ракетной техники. Из-за сложности и утомительного характера вычислений читателям этого веб-сайта был предложен более простой метод. Доступен ряд диаграмм сгорания топлива, из которых можно получить оптимальное соотношение смеси, температуру адиабатического пламени, молекулярную массу газа и удельную теплоемкость для некоторых распространенных ракетных топлив. Эти диаграммы были разработаны с использованием методов, описанных в этой статье. Энтальпия Энтальпия является мерой полной энергии термодинамической системы. Он включает в себя внутреннюю энергию, которая представляет собой энергию, необходимую для создания системы, и количество энергии, необходимое для того, чтобы освободить для нее место путем смещения окружающей среды и создания ее объема и давления. Энтальпия является предпочтительным выражением изменения энергии системы во многих химических, биологических и физических измерениях, поскольку она упрощает некоторые описания передачи энергии. Это связано с тем, что изменение энтальпии учитывает энергию, передаваемую окружающей среде при расширении исследуемой системы. Общая энтальпия H системы не может быть измерена напрямую. Таким образом, изменение энтальпии ΔH является более полезной величиной, чем ее абсолютное значение. Изменение ΔH положительно в эндотермических реакциях и отрицательно в тепловыделяющих экзотермических процессах. ΔH системы равен сумме немеханической работы, совершенной над ней, и подведенного к ней тепла. Для квазистатических процессов при постоянном давлении ΔH равно изменению внутренней энергии системы плюс работа, которую система совершила над своим окружением. В то время как H обозначает общую энтальпию системы, h представляет собой удельную энтальпию, то есть энтальпию на моль или единицу массы вещества. Мы просто будем называть оба значения энтальпией, поскольку из контекста ясно, что применимо. Энтальпия образования, или тепла, или образования, h o f , представляет собой энтальпию вещества при базовых условиях 25 o C и давлении 0,1 МПа. Энтальпию в любом другом состоянии по отношению к этому основанию можно найти, добавив изменение энтальпии между 25 o С и 0,1 МПа и данного состояния к энтальпии образования. , где член (Δh) 298,0,1 МПа –> T,P представляет собой разницу энтальпии между любым данным состоянием и энтальпией при 298,15 К, 0,1 МПа. Для удобства мы обычно опускаем индексы в следующих примерах. В большинстве случаев вещества, входящие в состав реагентов и продуктов химической реакции, не находятся при температуре 25 o С и давлении 0,1 МПа. Поэтому изменение энтальпии между 25 o С и 0,1 МПа и данным состоянием должно быть известно. В случае твердого тела или жидкости это изменение энтальпии обычно можно найти из таблицы термодинамических свойств или из данных об удельной теплоемкости. В случае газов это изменение энтальпии можно найти следующим образом: Предположим, что поведение идеального газа находится между 25 o C, 0,1 МПа и заданным состоянием. NIST Chemistry WebBook содержит уравнения для (h o -h o 298 ) и C p o для большинства веществ, а таблицы можно создать с помощью веб-сайта NIST-JANAF Termochemical Tables. (h o -h o 298 ) равно Δh, где h o 298 относится к 25 o C или 298,15 K. при давлении 0,1 МПа, исходя из поведения идеального газа, то есть энтальпии стандартного состояния. Когда отклонение от поведения идеального газа значительно, необходимо использовать другие процедуры, но в нашем случае это не обязательно. Адиабатическая температура пламени Рассмотрим данный процесс горения, который происходит адиабатически и не требует работы или изменения кинетической или потенциальной энергии. В следующем примере показано, как можно определить температуру адиабатического пламени. Происходящая в продуктах горения диссоциация, оказывающая существенное влияние на адиабатическую температуру пламени, будет рассмотрена в следующем разделе. Предположим, мы реагируем стехиометрической смесью газообразного метана и газообразного кислорода при начальной температуре 25 o С и давлении 4 МПа. Мы предполагаем идеальное поведение газа для всех компонентов. В этом случае первый закон термодинамики сводится к где H R – энтальпия реагентов, H P энтальпия продуктов, h o f энтальпия образования каждого компонента, Δh i изменение энтальпии каждого компонента в реагентах при начальной температуре, а Δh e изменение энтальпии каждого компонента в продуктах при адиабатической температуре пламени. Ниже в таблице приведены энтальпии образования и энтальпии идеального газа для нескольких продуктов, образующихся в результате реакции метан/кислород. Для продуктов у нас есть Методом проб и ошибок найдена температура продуктов, удовлетворяющая этому уравнению. Поскольку H P > H R , предполагаемая температура слишком высока. Давайте теперь попробуем Т P = 5200 К. Теперь мы можем интерполировать, чтобы найти адиабатическую температуру пламени. Криогенные реагенты Из предыдущего примера видно, что начальная температура реагентов влияет на конечную температуру продуктов. Для хранимого топлива колебания температуры жидкости в пределах нормального диапазона оказывают лишь незначительное влияние на характеристики двигателя. Криогенное топливо — это отдельная история, так как его чрезвычайно низкие температуры оказывают значительное влияние на характеристики. Мы должны также принять во внимание, что легкодоступные термохимические данные для этих веществ относятся к газообразному состоянию, а не к жидкости. Корректировка должна быть сделана для учета изменения состояния. Рассмотрим пример криогенного кислорода, температура кипения которого составляет -183 o С (90 К). Начнем с газообразного кислорода при 298 К, энтальпия образования которого равна 0 кДж/моль. Химическое равновесие Обратимся теперь к химическому равновесию. Здесь мы будем рассматривать химическую реакцию с участием только одной фазы, которая называется гомогенной химической реакцией. В нашем случае мы будем рассматривать газообразную фазу, но основные соображения применимы к любой фазе. Рассмотрим сосуд, содержащий четыре соединения A, B, C, и D, , которые находятся в химическом равновесии при заданных давлении и температуре. , где v — стехиометрические коэффициенты. Следует подчеркнуть, что существует вполне определенная связь между и (стехиометрическими коэффициентами), тогда как n (число присутствующих молей) для любого компонента можно варьировать, просто изменяя количество этого компонента. компонента в реакционном сосуде. Чтобы определить равновесный состав для химической реакции, мы должны уметь определять активность различных компонентов смеси. Мы делаем это, применяя понятие константы равновесия, К . Предполагая модель идеального газа, которая будет подходящей для наших примеров и приложений, уравнение химического равновесия может быть записано как , где y — равновесная мольная доля компонентов A, B, C и D, v — стехиометрический коэффициент для каждого компонента, а член P/P o представляет отношение давлений, при которых протекает реакция происходит до стандартного состояния давления. Уравнение записано в таком виде, потому что оно достаточно ясно демонстрирует влияние различных факторов на равновесный состав ( и -е). То есть мы знаем, что и температура, и давление влияют на равновесный состав. Видно, что влияние температуры входит через значение K (зависит только от температуры) и влияние давления через термин (P/P o ) V C +V D -V A -V B . Следует отметить, что равновесие продуктов сгорания очень чувствительно к температуре. Теперь вернемся к нашему предыдущему примеру и воспользуемся процедурой определения равновесного состава продуктов сгорания. Весь процесс удобно рассматривать так, как если бы он происходил в два отдельных этапа: процесс горения с последующим нагревом и диссоциацией продуктов сгорания. Реакция горения Есть несколько реакций диссоциации, которые вступят в игру, но мы рассмотрим две наиболее доминирующие в этом конкретном примере. То есть энергия, выделяющаяся при сгорании СН 4 и О 2 , нагревает СО 2 и Н 2 О до высокой температуры, в результате чего происходит диссоциация части СО 2 до СО и O 2 , и часть H 2 O до H 2 и OH. где неизвестные коэффициенты a, b, c, d, e, и f должны быть найдены путем решения уравнений равновесия, связанных с реакциями диссоциации. Из реакции горения мы находим, что начальные составы для реакций диссоциации: 1 моль CO 2 и 2 моля H 2 O. Поэтому, полагая z’ числом молей диссоциированного СО 2 , а z” числом молей диссоциированного H 2 O, находим Таким образом, общая реакция И общее количество молей в равновесии для каждой реакции равно Равновесные мольные доли Подставляя эти величины вместе с P = 4 МПа, получаем уравнения равновесия. Значения констант равновесия приведены в следующей таблице: Предположим, что T P = 3600 К, мы имеем Предположим, что T P = 3800 K, и повторите. Расчет адиабатической температуры пламени путем интерполяции. Зная температуру, теперь мы можем интерполировать, чтобы найти соответствующие значения ln(K) и рассчитать равновесную смесь. Для более точного решения необходимо учитывать дополнительные реакции диссоциации, такие как Из этого довольно простого примера видно, что учет всех возможных диссоциаций требует решения очень многих одновременных уравнений. Ниже приведено решение STANJAN для того же примера с метаном/кислородом, который мы рассматривали. Обратите внимание, что после учета всех диссоциаций конечная адиабатическая температура пламени была снижена до 3553,87 К. Средняя молекулярная масса смеси M просто равна , где n — общее количество молей в смеси, а m — общая масса смеси. Общее количество молей и общая масса находятся по формуле , где n i — количество молей каждого компонента, M i — молекулярный вес каждого компонента. Возвращаясь к последней итерации нашего уравнения горения, мы имеем Вычисляя молекулярную массу смеси, имеем Альтернативно, если молярная доля y i каждого компонента дана, где y i = n i / n , средняя молекулярная масса находится по формуле Ссылаясь на прогон STANJAN выше, мы можем видеть, что даны как мольная доля, так и молекулярная масса газа, где M = 22,519 кг/кмоль. Это ниже, чем наша производная единица, потому что в нашем примере не были учтены все применимые диссоциации. Коэффициент удельной теплоемкости Удельная теплоемкость или теплоемкость при постоянном давлении, C стр. , где ч — удельная энтальпия, u — удельная внутренняя энергия, T — температура. Очень важное соотношение между удельной теплоемкостью идеального газа при постоянном давлении и постоянном объеме находится в уравнении , где C p и C v выражены в молях, а R’ – универсальная газовая постоянная (8,31446 Дж/моль-К). Это говорит нам о том, что разница между удельной теплоемкостью идеального газа при постоянном давлении и постоянном объеме всегда постоянна, хотя обе они являются функцией температуры. Многие термодинамические решения используют отношение удельных теплоемкостей, k или , определяемое как Поскольку в справочниках по термодинамике принято указывать только значение C p , из которого рассчитывается C v , мы можем объединить уравнения и записать Значения удельной теплоемкости при постоянном давлении обычно находятся с помощью уравнения или из табличных значений C p в зависимости от температуры. Когда у нас есть смесь газов, мы должны определить удельную теплоемкость смеси, где Рассчитаем удельную теплоемкость смеси газов, найденной в решении STANJAN для нашей задачи метан/кислород, учитывая, что температура равна 3553,87 К. Хотя некоторые компьютерные программы рассчитывают значение коэффициента теплоемкости, STANJAN этого не делает. Если используется STANJAN, пользователю придется вычислять k отдельно, хотя это можно легко сделать с помощью программного обеспечения для работы с электронными таблицами. Конденсированные виды До сих пор все предполагало, что продукты сгорания состоят из гомогенной смеси газов. При работе с жидким ракетным топливом это справедливое допущение, поскольку любые конденсированные вещества (будь то жидкости или твердые вещества) будут появляться только в следовых количествах. Однако при работе с твердым топливом значительная часть продуктов выхлопа будет находиться в конденсированной фазе, что проявляется в виде видимого дыма в выхлопном шлейфе. Когда продукты существуют более чем в одной фазе, говорят, что смесь гетерогенна. Неоднородность требует, чтобы мы изменили метод расчета молекулярной массы и удельной теплоемкости. Двухфазные уравнения, представленные ниже, получены Ричардом Наккой и описаны на его веб-сайте Experimental Rocketry . Необходимое ключевое допущение состоит в том, что частицы конденсированной фазы текут с той же скоростью, что и газ (т. е. без отставания по скорости), поэтому модифицированные уравнения представляют собой верхний предел производительности. Детали слишком сложны, чтобы представлять их здесь, поэтому представлен только окончательный результат, который, к счастью, довольно прост. Как оказалось, смесь газов с частицами ведет себя как газ с измененным коэффициентом теплоемкости к . Все основные уравнения остаются прежними и полностью применимы к двухфазному потоку, за исключением следующих изменений: где С стр смесь – эффективная удельная теплоемкость смеси газа и конденсированной фазы, определяемая выражением , где n i – количество молей газового компонента, i , n s – количество молей конденсированного компонента, а n – общее количество молей газа. k смесь – форма, используемая при расчете давления в камере сгорания и характеристической скорости выхлопа. Там, где скорость и ускорение потока большие, т. е. в сопле, имеем , где k’ — удельная теплоемкость смеси только газов; Ψ = ш s /(1–w s ), где w s – массовая доля частиц конденсированной фазы в выхлопе; C s – удельная теплоемкость твердой (или жидкой) смеси в выхлопе; и C p gas – удельная теплоемкость смеси только газов. Как прежде, Вывод этой формы модифицированного коэффициента удельной теплоемкости предполагает состояние замороженного потока, при котором не предполагается существование теплового или скоростного отставания частиц, и основан на уравнениях количества движения и энергии для установившегося изоэнтропического потока. k 2ph — это форма, используемая при расчете скорости истечения, тяги, коэффициента тяги и других параметров расхода сопла. Ссылаясь на «мольную долю в смеси» в анализе STANJAN, мы находим А из «массовой доли в смеси» находим массовую долю конденсированных частиц, Вычисляя общую массу, имеем Следовательно, Далее находим Наконец, мы вычисляем удельные теплоемкости, Когда использовать k mix по сравнению с k 2ph Ссылаясь на страницу «Ракетный двигатель», при наличии конденсированных частиц необходимо решить следующие уравнения, используя k микс : И следующее должно быть решено с помощью k 2ph : Изэнтропическое сжатие и расширение Здесь мы приводим два важных уравнения, которые связывают давление, температуру и объем, занимаемый газом при обратимом сжатии или расширении. При изоэнтропическом сжатии и расширении влияние давления на температуру описывается выражением и влияние объема на давление где T 1 , p 1 и v 1 — начальные температура, давление и объем; T 2 , p 2 и v 2 – конечные температура, давление и объем; k – коэффициент удельной теплоемкости. Мы также можем комбинировать уравнения, чтобы найти влияние объема на температуру Поскольку расширение выхлопных газов через сопло ракеты является изоэнтропическим процессом, применимы приведенные выше уравнения. Скажем, например, мы хотим знать температуру на выходе из сопла для ракетного двигателя, имеющего температуру в камере 3250 К, давление в камере 6 МПа, давление на выходе из сопла 0,07 МПа, и известно, что k 1.23. У нас есть СТАНДЖАН Если вы решите попробовать STANJAN, у меня есть несколько полезных советов, извлеченных из моего опыта использования. Это не инструкция по использованию программного обеспечения. Во-первых, STANJAN поставляется с файлом с именем TURBINE.DOC, который является примером запуска STANJAN для проблемы с газовой турбиной. Во-вторых, STANJAN поставляется с ограниченным числом файлов данных о видах, поэтому вам, безусловно, придется создать несколько собственных, если вы планируете серьезно относиться к использованию программного обеспечения. В комплект поставки STANJAN входит файл SPECIES.DOC, в котором объясняется, как форматируются файлы данных. Ниже приведен отрывок, показывающий образец ввода данных для двуокиси углерода. Файлы данных можно легко редактировать и/или создавать в текстовом редакторе, таком как Блокнот или WordPad . Значения, заполняющие файлы данных, можно найти и/или рассчитать с помощью веб-книги по химии NIST или, что еще проще, с помощью термохимических таблиц NIST-JANAF. Однако имейте в виду, что в файлах данных STANJAN вместо джоулей используются единицы измерения калорий. Вам определенно нужно будет создать свои собственные файлы данных для реагентов, так как STANJAN не включает в себя какое-либо обычное ракетное топливо. Однако есть короткий путь, который значительно упрощает эту задачу. Если вы всегда предполагаете, что ваши реагенты имеют начальную температуру 298,15 К, т. е. базовую температуру, нет необходимости заполнять файлы данных всеми S и H-H(298.15) , поскольку они используются только тогда, когда температура отличается от 298,15 K. Вам необходимо заполнить данные только в первой строке, чтобы ваши файлы данных реагентов выглядели так, как показано в следующем примере для метилгидразина. : Решение — простой трюк; в поле, где вы обычно вводите энтальпию образования, замените ее энтальпией криогенной жидкости при ее температуре кипения. Ранее я продемонстрировал это при расчете энтальпии LOX, равной -12,88 кДж/моль, или -3,078 ккал/моль. Теперь при вводе температуры 298,15 К вы фактически получите энтальпию криогенной жидкости. Наконец, мне нравится создавать отдельные файлы данных для реагентов и продуктов. А для продуктов мне нравится создавать несколько файлов данных, каждый из которых представляет отдельную группу элементов. Например, у меня есть файлы данных HO.DAT, CHO.DAT, CHNO.DAT и т. д. Таким образом, если моя реакция содержит только элементы C, H и O, я выберу файл CHO.DAT, который содержит все составляющие, нормальные для такой реакции – C, CO, CO 2 , Н, Н 2 , НО, Н 2 О, О и О 2 .
Жидкость Коэффициент пленки
(БТЕ/час-фут 2 -F) Пар 1000 – 3000 Органические растворители 150 – 500 Легкие масла 200 – 400 Тяжелые масла (вакуум) 20 – 50 Аммиак 500 – 1000 Свойства выхлопных газов Единицы МКССИФПС выберите Газ GT ExhaustSA установка I PassSA установка II PassBlrExh-OilFiredBlrExh-WoodFiredBlrExh-LigniteBlrExh-BagasseBlrExh-Coal FiredBlrExh-Nat.  GasBlrExh-Refin.GasBlrExh-OilGasBlrExh-CO.GasBlrExh-BF.GasBlrExh0GasBlrExh-ProBl02GasGasBlrExh-Prob.Wat.
GasBlrExh-Refin.GasBlrExh-OilGasBlrExh-CO.GasBlrExh-BF.GasBlrExh0GasBlrExh-ProBl02GasGasBlrExh-Prob.Wat. выберите Средняя температура газа: град С SO2: SO3: О2: N2: СО2: СО: h3O: h3: Проводимость: ккал/(ч.  м.ч)
м.ч) Динамическая вязкость: кг/(м.с) Кинематическая вязкость: м2/с Нормальная плотность: кг/м3 Плотность: кг/м3 Удельная теплоёмкость: ккал/(кг.  с)
с) Единицы входных данных: MKS – Temp-degC ; СИ – Темп-градусы Цельсия; FPS – Temp-degF Единицы МКС: Темп-°C; Электропроводность-Ккал/ч/м/Кл; Дин. Вязкость-кг/м/с; Кин.Вязкость-м²/с; Sp.Heat-Kcal/Kg/C; Плотность-кг/м³; Давление – кг/см²; теплотворная способность-ккал/кг Свойства газа
Что это
Расчеты показывают свойства газа при различных температурах.
Это основные свойства газа, которые обычно доступны в таблицах газа. Свойства газа необходимы для расчета теплопередачи со стороны газа, тепловой нагрузки различных устройств, таких как котлы, термические жидкостные нагреватели, испарители и т. д. Эти свойства необходимы для определения размеров различного оборудования в перерабатывающей промышленности.
д. Эти свойства необходимы для определения размеров различного оборудования в перерабатывающей промышленности.
Пользователь может выбрать любую из единиц измерения, а затем ввести входные данные, такие как состав газа и температура. Как только пользователь нажимает кнопку RUN>>, программное обеспечение вычисляет необходимые параметры и отображает выходные данные. Выходные данные состоят из различных свойств газа, таких как проводимость газа, динамическая вязкость газа, кинематическая вязкость газа, удельная теплоемкость и плотность газа 9.0007 Ракетная термодинамика
РАКЕТНАЯ ТЕРМОДИНАМИКА  Пока известны температура, молекулярный вес, удельная теплоемкость продуктов выхлопа, уравнения ракеты могут быть решены. Однако часто бывает полезно иметь возможность вывести эти величины для себя. В этой статье мы даем обзор химической термодинамики, применимой к ракетным двигателям. Предполагается, что читатель имеет хотя бы элементарное представление о термодинамике, поскольку в наши намерения не входит полное объяснение ее основ.
Пока известны температура, молекулярный вес, удельная теплоемкость продуктов выхлопа, уравнения ракеты могут быть решены. Однако часто бывает полезно иметь возможность вывести эти величины для себя. В этой статье мы даем обзор химической термодинамики, применимой к ракетным двигателям. Предполагается, что читатель имеет хотя бы элементарное представление о термодинамике, поскольку в наши намерения не входит полное объяснение ее основ. Единицей измерения энтальпии в Международной системе единиц (СИ) является джоуль, но до сих пор используются другие исторические общепринятые единицы, такие как БТЕ и калория.
Единицей измерения энтальпии в Международной системе единиц (СИ) является джоуль, но до сих пор используются другие исторические общепринятые единицы, такие как БТЕ и калория. Это означает, что изменение энтальпии в таких условиях представляет собой тепло, поглощенное (или выделившееся) в результате химической реакции. Энтальпии для химических веществ при постоянном давлении принимают стандартное состояние: чаще всего давление 1 бар (0,1 МПа). Стандартное состояние, строго говоря, не определяет температуру, но выражения для энтальпии обычно ссылаются на стандартную энтальпию образования при 25°С.0400 o С (298,15 К).
Это означает, что изменение энтальпии в таких условиях представляет собой тепло, поглощенное (или выделившееся) в результате химической реакции. Энтальпии для химических веществ при постоянном давлении принимают стандартное состояние: чаще всего давление 1 бар (0,1 МПа). Стандартное состояние, строго говоря, не определяет температуру, но выражения для энтальпии обычно ссылаются на стандартную энтальпию образования при 25°С.0400 o С (298,15 К). То есть энтальпия при любой температуре и давлении h T,P равна
То есть энтальпия при любой температуре и давлении h T,P равна В этом случае энтальпия является функцией только температуры и может быть найдена с помощью уравнения из табличных значений энтальпии как функции температуры (что предполагает поведение идеального газа) или рассчитана из удельной теплоемкости C р o , где
В этом случае энтальпия является функцией только температуры и может быть найдена с помощью уравнения из табличных значений энтальпии как функции температуры (что предполагает поведение идеального газа) или рассчитана из удельной теплоемкости C р o , где Для такого процесса температуру продуктов называют адиабатической температурой пламени. При допущении отсутствия работы и изменений кинетической или потенциальной энергии это максимальная температура, которая может быть достигнута для данных реагентов, потому что любой перенос тепла от реагирующих веществ и любое неполное сгорание будут иметь тенденцию к понижению температуры продуктов. Для данного топлива и данных давления и температуры реагентов максимальная адиабатическая температура, которая может быть достигнута, достигается при использовании стехиометрической смеси.
Для такого процесса температуру продуктов называют адиабатической температурой пламени. При допущении отсутствия работы и изменений кинетической или потенциальной энергии это максимальная температура, которая может быть достигнута для данных реагентов, потому что любой перенос тепла от реагирующих веществ и любое неполное сгорание будут иметь тенденцию к понижению температуры продуктов. Для данного топлива и данных давления и температуры реагентов максимальная адиабатическая температура, которая может быть достигнута, достигается при использовании стехиометрической смеси. Наше уравнение реакции
Наше уравнение реакции Заметим, что в рассмотренной выше упрощенной реакции имеем только CO 2 и H 2 O в правой части уравнения. Дополнительные вещества появятся, когда мы будем рассматривать диссоциацию в следующем разделе.
Заметим, что в рассмотренной выше упрощенной реакции имеем только CO 2 и H 2 O в правой части уравнения. Дополнительные вещества появятся, когда мы будем рассматривать диссоциацию в следующем разделе. Температура
К Метан
CH 4
(31.03.61) Двуокись углерода
CO 2
(30.09.65) Монооксид углерода
CO
(30.09.65) Кислород двухатомный
O 2
(30.09.65) Вода (газ)
H 2 O
(31.03.61) Водород, двухатомный
H 2
(31.03.61) Гидроксил
ОН
(31.03.66) (h f o ) 298 = -74,873
M = 16,043 (h f o ) 298 = -393,522
M = 44,010 (ч ж или ) 298 = -110,529
М = 28,010 (h f o ) 298 = 0
M = 31,999 (h f o ) 298 = -241,827
M = 18,015 (h f o ) 298 = 0
М = 2,0159 (h f o ) 298 = 39,463
M = 17,007 (ч о -ч о 298 )
кДж/моль (h o -h o 298 )
кДж/моль (h o -h o 298 )
кДж/моль (h o -h o 298 )
кДж/моль (h o -h o 298 )
кДж/моль (h o -h o 298 )
кДж/моль (ч o -h o 298 )
кДж/моль 0 -10.  024
024 -9,364 -8,669 -8,682 -9,904 -8,468 -9.171 100 -6,698 -6,456 -5,770 -5,778 -6,615 -5,293 -6,138 200 -3,368 -3,414 -2,858 -2,866 -3,280 -2,770 -2,975 298 0,000 0,000 0,000 0,000 0,000 0,000 0,000 300 0,066 0,067 0,054 0,054 0,063 0,054 0,054 400 3,861 4.  008
008 2,975 3,029 3,452 2,958 3,033 500 8.200 8.314 5,929 6.088 6,920 5,883 5,991 600 13.130 12,916 8,941 9.247 10.498 8.812 8,941 700 18.635 17,761 12.021 12.  502
502 14.184 11.749 11.903 800 24.675 22.815 15.175 15.841 17,991 14.703 14.878 900 31.205 28.041 18.397 19.246 21,924 17.682 17.887 1000 38.179 33.405 21.686 22.707 25,978 20,686 20,933 1100 45,549 38.  894
894 25.033 26.217 30,167 23,723 24.025 1200 53.270 44.484 28.426 29,765 34.476 26,794 27.158 1300 61.302 50,158 31.865 33.351 38,903 29.907 30.342 1400 69,608 55,907 35,338 36,966 43.  447
447 33.062 33,568 1500 78.153 61,714 38,848 40.610 48.095 36,267 36.840 1600 86,910 67,580 42,384 44,279 52,844 39,522 40.150 1700 95,853 73,492 45,940 47,970 57,685 42.815 43.  501
501 1800 104,960 79.442 49,522 51,689 62,609 46.150 46.890 1900 114,212 85.429 53.124 55.434 67,613 49,522 50.308 2000 123,592 91.450 56,739 59,199 72,689 52,932 53,760 2100 133.  087
087 97.500 60,375 62,986 77,831 56,379 57.241 2200 142,684 103,575 64.019 66.802 83.036 59.860 60,752 2300 152,371 109,671 67,676 70,634 88,295 63,371 64,283 2400 162,141 115,788 71,346 74,492 93,604 66,915 67,839 2500 171,984 121,926 75.  023
023 78,375 98,964 70.492 71.417 2600 181,893 128.085 78,714 82,274 104.370 74.090 75.015 2700 191,862 134,256 82.408 86.199 109.813 77,718 78,634 2800 201,885 140,444 86.115 90.  144
144 115,294 81.370 82,266 2900 211,958 146,645 89,826 94.111 120,813 85.044 85,918 3000 222.076 152,862 93,542 98.098 126,361 88,743 89,584 3200 242.431 165,331 100,998 106,127 137,553 96.  199
199 96,960 3400 262,925 177,849 108.479 114,232 148,854 103,738 104,387 3600 283,536 190.405 115,976 122,399 160,247 111.361 111,859 3800 304,248 202,999 123,495 130,629 171,724 119.064 119,378 4000 325.  045
045 215,635 131.026 138,913 183,280 126,846 126,934 4200 345,918 228.304 138,578 147,248 194,903 134.700 134,528 4400 366,855 241.003 146,147 155,628 206,585 142,624 142,156 4600 387,849 253,734 153,724 164.  046
046 218,325 150,620 149,816 4800 408.893 266.500 161,322 172,502 230.120 158,682 157,502 5000 429,982 279,295 168,929 180,987 241,957 166,808 165,222 5200 451.110 292,123 176,548 189,502 253,839 174,996 172,967 5400 472,274 304,984 184,184 198.  037
037 265,768 183,247 180,736 5600 493,469 317,884 191,832 206,593 277,738 191,556 188,531 5800 514,692 330,821 199,489 215,166 289,746 199,924 196,351 6000 535,942 343,791 207,162 223,756 301,796 208,346 204,192 Термохимические данные рассчитаны на основе термохимических таблиц JANAF,
Лаборатория термических исследований, The Dow Chemical Company, Мидленд, Мичиган.
Указана дата выпуска каждой таблицы.
Зная температуру реагентов, легко вычислить H R . Так как температура реагентов в нашем примере равна базовой температуре 25 o С, то Δh i = 0 и нам остается только просуммировать энтальпии образования реагентов. Из таблицы выше видим, что для двухатомного кислорода (h f o ) 298 = 0, что характерно для двухатомных газов, а для метана находим (h f o ) 298 = -74,873 кДж/моль. Таким образом, у нас есть Предположим, мы уже провели несколько испытаний и начали оттачивать решение. Для следующего испытания предположим, что T P = 5400 К.
Предположим, мы уже провели несколько испытаний и начали оттачивать решение. Для следующего испытания предположим, что T P = 5400 К. Для гиперголов а 10 o C Изменение температуры реагента приводит к изменению удельного импульса примерно на 0,1%. Поэтому мы можем с уверенностью предположить, что начальная температура хранимых порохов является стандартной энтальпией температуры образования 25 o C. Это предположение имеет дополнительное преимущество, заключающееся в упрощении расчетов, поскольку нам нужно только искать энтальпии образований для реагентов без дополнительной корректировки температуры.
Для гиперголов а 10 o C Изменение температуры реагента приводит к изменению удельного импульса примерно на 0,1%. Поэтому мы можем с уверенностью предположить, что начальная температура хранимых порохов является стандартной энтальпией температуры образования 25 o C. Это предположение имеет дополнительное преимущество, заключающееся в упрощении расчетов, поскольку нам нужно только искать энтальпии образований для реагентов без дополнительной корректировки температуры. Затем мы добавляем изменение энтальпии, необходимое для понижения температуры с 298 К до 90 К. Из таблиц энтальпий мы оцениваем, что это изменение составляет -6,06 кДж/моль. Затем мы вычитаем энтальпию испарения, чтобы учесть изменение состояния из газа в жидкость. Энтальпия испарения кислорода 6,82 кДж/моль. Следовательно, энтальпия жидкого кислородного реагента равна
Затем мы добавляем изменение энтальпии, необходимое для понижения температуры с 298 К до 90 К. Из таблиц энтальпий мы оцениваем, что это изменение составляет -6,06 кДж/моль. Затем мы вычитаем энтальпию испарения, чтобы учесть изменение состояния из газа в жидкость. Энтальпия испарения кислорода 6,82 кДж/моль. Следовательно, энтальпия жидкого кислородного реагента равна Обозначим количество молей каждого компонента n A , n B , n C , и n D . Далее, пусть химическая реакция, происходящая между этими четырьмя составляющими, будет
Обозначим количество молей каждого компонента n A , n B , n C , и n D . Далее, пусть химическая реакция, происходящая между этими четырьмя составляющими, будет V B 9000. 9000. 9000. 9000. 9000. V B 9000. V A . ) × (P/P или ) V C +V D -V A -V B
V B 9000. 9000. 9000. 9000. 9000. V B 9000. V A . ) × (P/P или ) V C +V D -V A -V B  Продукты, существующие при высокой температуре горения, сильно отличаются от тех, что существуют при более низкой температуре горения. При высоких температурах происходит диссоциация продуктов, так как тепловая энергия вызывает распад молекул на более простые и одноатомные составляющие. Реакции диссоциации обратимы (на что указывает двойная стрелка в уравнениях), поэтому при охлаждении газов может происходить рекомбинация.
Продукты, существующие при высокой температуре горения, сильно отличаются от тех, что существуют при более низкой температуре горения. При высоких температурах происходит диссоциация продуктов, так как тепловая энергия вызывает распад молекул на более простые и одноатомные составляющие. Реакции диссоциации обратимы (на что указывает двойная стрелка в уравнениях), поэтому при охлаждении газов может происходить рекомбинация. Таким образом, общую реакцию можно записать
Таким образом, общую реакцию можно записать
CO 2 CO + 1/2 O 2
Исходный: 1 0 0
Изменить: -z' +z' +z'/2
_____________________________________________
В состоянии равновесия: (1-z') z' z'/2
Н 2 O 1/2H 2 + OH
Исходный: 2 0 0
Изменить: -z" +z"/2 +z"
_____________________________________________
В состоянии равновесия: (2-z") z"/2 z"

Логарифмы по основанию e константы равновесия K Температура
К CO 2 = CO + 1/2 O 2 H 2 O = 1/2 H 2 + OH 298 -103,762 -106.  208
208 500 -57,616 -60,281 1000 -23,529 -26.034 1200 -17,871 -20.283 1400 -13,842 -16.099 1600 -10.830 -13.066 1800 -8,497 -10,657 2000 -6,635 -8,728 2200 -5.120 -7,148 2400 -3,860 -5,832 2600 -2,801 -4,719 2800 -1,894 -3,763 3000 -1.  111
111 -2,937 3200 -0,429 -2,212 3400 0,169 -1,576 3600 0,701 -1,009 3800 1,176 -0,501 4000 1,599 -0,044 4500 2,490 0,920 5000 3,197 1,689 5500 3,771 2,318 6000 4,245 2,843
Методом проб и ошибок должна быть найдена температура продуктов, удовлетворяющая уравнениям. Шаги
Шаги383

 Попробуйте добавить в смесь еще один элемент, например азот, и мы еще больше усложним задачу. Быстрое и простое предоставление точных решений возможно только с помощью компьютерной программы. Одной из таких программ является бесплатная программа STANJAN, написанная бывшим профессором Стэнфордского университета Уильямом С. Рейнольдсом, © 1984.
Попробуйте добавить в смесь еще один элемент, например азот, и мы еще больше усложним задачу. Быстрое и простое предоставление точных решений возможно только с помощью компьютерной программы. Одной из таких программ является бесплатная программа STANJAN, написанная бывшим профессором Стэнфордского университета Уильямом С. Рейнольдсом, © 1984.
Независимый относительный элемент
популяционный потенциал системного атома
С 1.00000000E+00 -16.8393
О 4.00000000Е+00 -14,9514
Н 4.00000000Е+00 -10.3070
Состав при T = 3553,87 K P = 3,948E+01 атмосферы
виды мольная доля массовая доля мольная доля
в газе в смеси в смеси
газовая фаза
СО . 14455E+00 .17980E+00 .14455E+00
СО2 .13679E+00 .26734E+00 .13679E+00
Н .25470Е-01 .11400Е-02 .25470Е-01
НО .
14455E+00 .17980E+00 .14455E+00
СО2 .13679E+00 .26734E+00 .13679E+00
Н .25470Е-01 .11400Е-02 .25470Е-01
НО .
Молекулярный вес
 и удельная теплоемкость при постоянном объеме C v являются полезными функциями для термодинамических расчетов, особенно для газов, и определяются следующими соотношениями
и удельная теплоемкость при постоянном объеме C v являются полезными функциями для термодинамических расчетов, особенно для газов, и определяются следующими соотношениями Обычно используется уравнение Шомейта, которое показано ниже вместе с коэффициентами Шомейта продуктов, найденных в нашем примере сгорания.
Обычно используется уравнение Шомейта, которое показано ниже вместе с коэффициентами Шомейта продуктов, найденных в нашем примере сгорания. Теплоемкость газовой фазы (уравнение Шомате) C p o = A + Bt + Ct 2 + Dt 3 + E/t 2
где Cp = теплоемкость (Дж/моль-К), t = температура (К) / 1000 Формула Темп. Диапазон А Б С Д Е СО 2 1200-6000 58.16639 2.720074 -0,4 0,038844 -6.  447293
447293 СО 1300-6000 35.15070 1.300095 -0,205921 0,013550 -3.282780 Н 2 О 1700-6000 41,96426 8.62253 -1,499780 0,098119 -11.15764 Н 2 2500-6000 43.413560 -4.2 1.272428 -0,096876 -20,533862 Х 298-6000 20.  78603
78603 4,850638×10 -10 -1,582916×10 -10 1.525102×10 -11 3.196347×10 -11 О 2 2000-6000 20. 10.72071 -2.020498 0,146449 9.245722 О 2500-6000 22.18977 -1.318044 0,378308 -0,026069 0 ОХ 1300-6000 28.74701 4.  714489
714489 -0,814725 0,054748 -2,747829 Коэффициенты Shomate взяты из веб-книги NIST Chemistry WebBook,
, за исключением одноатомного кислорода (O), полученного Р.А. Braeunig из данных, найденных здесь.
Расчет коэффициента удельной теплоемкости отдельного вещества прост. Скажем, у нас есть угарный газ при температуре 3000 К, удельная теплоемкость равна




Теперь рассмотрим пример. Ниже приведен прогон STANJAN для сжигания 68% перхлората аммония, 18% алюминия и 14% HTPB при давлении в камере 4 МПа.
Независимый относительный элемент
популяционный потенциал системного атома
Ал 6.67111407Э-01 -16.5165
Кл 5.78772661Э-01-20.5197
О 2.31509064Э+00 -19.0205
Н 3,86805792Е+00 -9,2472
С 1.03531152E+00 -12.1297
Н 5.78772661Э-01 -13.7827
Состав при Т = 3280,36 К Р = 3,948E+01 атмосфер
виды мольная доля массовая доля мольная доля
в газе в смеси в смеси
газовая фаза
Алюминий .15875E-03 .15634E-03 .14634E-03
AlCl .82935E-02 .18897E-01 .76450E-02
AlClO .13303E-02 . 38081E-02 .12263E-02
AlCl2 .22637E-02 .80879E-02 .20867E-02
AlCl3 .21732E-03 .10576E-02 .20033E-03
AlO .14196Э-03 .22269Э-03 .13086Э-03
AlOH .42786E-03 .68696E-03 .39441E-03
AlO(ОН) .29780E-03 .65205E-03 .27452E-03
СО .27553E+00 .28168E+00 .25398E+00
СО2 .81351E-02 .13067E-01 .74990E-02
Класс .82798E-02 .10713E-01 .76324E-02
Н .33101Е-01 .12178Е-02 .30513Е-01
HCl .13549E+00 .18031E+00 .12490E+00
НО .30828E-02 .19136Э-02 .28418Э-02
h3 .36159E+00 .26606E-01 .33332E+00
h3O .82105E-01 .53989E-01 .75685E-01
№ .18270E-03 .20010E-03 .16842E-03
N2 .79197E-01 .80974E-01 .73005E-01
О .16856Е-03 .98432Е-04 .15538Е-03
конденсированные виды
Al2O3(с) .31566E+00 .78192E-01
Свойства смеси: молярная масса газа = 18,750 кг/кмоль
T = 3280,363 K P = 4,0000E+06 Па V = 2,4894E-01 м**3/кг
U = -2,8456E+06 Дж/кг H = -1,8499E+06 Дж/кг S = 9,6821E+03 Дж/кг-K
Сделано 3 (Т,П) итерации; 11 конденсатных итераций; 54 прохода газа.
38081E-02 .12263E-02
AlCl2 .22637E-02 .80879E-02 .20867E-02
AlCl3 .21732E-03 .10576E-02 .20033E-03
AlO .14196Э-03 .22269Э-03 .13086Э-03
AlOH .42786E-03 .68696E-03 .39441E-03
AlO(ОН) .29780E-03 .65205E-03 .27452E-03
СО .27553E+00 .28168E+00 .25398E+00
СО2 .81351E-02 .13067E-01 .74990E-02
Класс .82798E-02 .10713E-01 .76324E-02
Н .33101Е-01 .12178Е-02 .30513Е-01
HCl .13549E+00 .18031E+00 .12490E+00
НО .30828E-02 .19136Э-02 .28418Э-02
h3 .36159E+00 .26606E-01 .33332E+00
h3O .82105E-01 .53989E-01 .75685E-01
№ .18270E-03 .20010E-03 .16842E-03
N2 .79197E-01 .80974E-01 .73005E-01
О .16856Е-03 .98432Е-04 .15538Е-03
конденсированные виды
Al2O3(с) .31566E+00 .78192E-01
Свойства смеси: молярная масса газа = 18,750 кг/кмоль
T = 3280,363 K P = 4,0000E+06 Па V = 2,4894E-01 м**3/кг
U = -2,8456E+06 Дж/кг H = -1,8499E+06 Дж/кг S = 9,6821E+03 Дж/кг-K
Сделано 3 (Т,П) итерации; 11 конденсатных итераций; 54 прохода газа.
Для выполнения расчетов нам нужны молекулярная масса и удельная теплоемкость каждого компонента. Следующее получено из веб-книги по химии NIST с клапанами C p , полученными для температуры камеры 3280,363 К.
Следующее получено из веб-книги по химии NIST с клапанами C p , полученными для температуры камеры 3280,363 К.
Вид MC p
г/моль Дж/моль-К
----------------------------------
Ал 26,982 20,7692
AlCl 62,435 39,0550
AlClO 78,434 62,2791
AlCl2 97,888 58,3019
AlCl3 133,341 83,0688
AlO 42,981 46,9917
АлОН 43,989 60,2511
AlO(ОН) 59,988 81,6723
СО 28.010 37.3728
СО2 44,010 62,5638
Кл 35,453 20,9928
Н 1,008 20,7860
HCl 36,461 37,5480
НО 17.007 37.1224
h3 2,016 37,6952
h3O 18,015 56,5356
№ 30.006 37.6115
N2 28.013 37.2055
О 15.999 21.0168
Al2O3(в) 101,961 192,4640
 Такой процесс происходит во время такта сжатия и рабочего такта двигателя внутреннего сгорания. Одни и те же уравнения описывают условия на компрессоре и турбине газовой турбины или на сопле ракетного двигателя. Результирующие сжатия и расширения являются обратимыми процессами, в которых энтропия системы остается постоянной. Такой процесс называется -изоэнтропическим -процессом.
Такой процесс происходит во время такта сжатия и рабочего такта двигателя внутреннего сгорания. Одни и те же уравнения описывают условия на компрессоре и турбине газовой турбины или на сопле ракетного двигателя. Результирующие сжатия и расширения являются обратимыми процессами, в которых энтропия системы остается постоянной. Такой процесс называется -изоэнтропическим -процессом.
 В нем описаны этапы определения адиабатической температуры пламени и результатов изоэнтропического расширения выхлопных газов. Научитесь следовать этому примеру, и вы сможете выполнять все расчеты, описанные в этой статье.
В нем описаны этапы определения адиабатической температуры пламени и результатов изоэнтропического расширения выхлопных газов. Научитесь следовать этому примеру, и вы сможете выполнять все расчеты, описанные в этой статье.
Название вида (8 знаков) Атомный состав:
Левое оправдание в столбце 1
| номер по правому краю
| Дата данных, за которым следует поле
| 8 символов, начиная с символов атома Col 10 (2 символа)
| | оставил оправданным в
| | Кол 19-28 поле (верхнее или нижнее
| | мол.
 вес, г/моль случае, но необходимо использовать
| | | те же символы для
| | | столбцы 29-38 с заданным атомом повсюду
| | | энт. сформировать файл данных). Должно быть
| | | на 298,15K, как показано ниже;
| | | ккал/моль 6(I3,A2) начиная с
| | | | кол 49.
| | | | Кол 39-48.
| | | | 0,0 для газа; .
| | | | плотность, г/см .
| | | | для жидкости или .
| | | | твердый ...............................
| | | | | | | | | | |
| | | | | | .. | .. | .. | .. | .. | ..
СО2 9/30/65 44,00995 -94,054 0,000 1С 2О 0 0 0 0
47,769 51,072 51,127 53,830 56,122 58,126 59,910 61,522 62,992 64,344
65,594 66,756 67,841 68,859 69,817 70,722 71,578 72,391 73,165 73,903
74,608 75,284 75,931 76,554 77,153 77,730 78,286 78,824 79,344 79,848
80,336 80,810 81,270 81,717 82,151 82,574 82,986 83,388 83,780 84,162
84,536 84,901 85,258 85,607 85,949 86,284 86,611 86,933 87,248 87,557
87,860 88,158 88,451 88,738 890,021 89,299 89,572 89,841 90,106 90,367
-0,816 0,000 0,016 0,958 1,987 3,087 4,245 5,453 6,702 7,984
9,296 10,632 11,988 13,362 14,750 16,152 17,565 18,987 20,418 21,857
23,303 24,755 26,212 27,674 29,141 30,613 32,088 33,567 35,049 36,535
38,024 39,515 41,010 42,507 44,006 45,508 47,012 48,518 50,027 51,538
53,051 54,566 56,082 57,601 59,122 60,644 62,169 63,695 65,223 66,753
68,285 69,819 71,355 72,893 74,433 75,976 77,521 79,068 80,617 82,168
Строки 2–7 представляют собой значения S(T,1 атм), кал/моль-К, считанные из JANNAF.
вес, г/моль случае, но необходимо использовать
| | | те же символы для
| | | столбцы 29-38 с заданным атомом повсюду
| | | энт. сформировать файл данных). Должно быть
| | | на 298,15K, как показано ниже;
| | | ккал/моль 6(I3,A2) начиная с
| | | | кол 49.
| | | | Кол 39-48.
| | | | 0,0 для газа; .
| | | | плотность, г/см .
| | | | для жидкости или .
| | | | твердый ...............................
| | | | | | | | | | |
| | | | | | .. | .. | .. | .. | .. | ..
СО2 9/30/65 44,00995 -94,054 0,000 1С 2О 0 0 0 0
47,769 51,072 51,127 53,830 56,122 58,126 59,910 61,522 62,992 64,344
65,594 66,756 67,841 68,859 69,817 70,722 71,578 72,391 73,165 73,903
74,608 75,284 75,931 76,554 77,153 77,730 78,286 78,824 79,344 79,848
80,336 80,810 81,270 81,717 82,151 82,574 82,986 83,388 83,780 84,162
84,536 84,901 85,258 85,607 85,949 86,284 86,611 86,933 87,248 87,557
87,860 88,158 88,451 88,738 890,021 89,299 89,572 89,841 90,106 90,367
-0,816 0,000 0,016 0,958 1,987 3,087 4,245 5,453 6,702 7,984
9,296 10,632 11,988 13,362 14,750 16,152 17,565 18,987 20,418 21,857
23,303 24,755 26,212 27,674 29,141 30,613 32,088 33,567 35,049 36,535
38,024 39,515 41,010 42,507 44,006 45,508 47,012 48,518 50,027 51,538
53,051 54,566 56,082 57,601 59,122 60,644 62,169 63,695 65,223 66,753
68,285 69,819 71,355 72,893 74,433 75,976 77,521 79,068 80,617 82,168
Строки 2–7 представляют собой значения S(T,1 атм), кал/моль-К, считанные из JANNAF. таблицы на 200, 298,15,300,400,500,....,6000 К.
Строки 8-13 представляют собой значения H-H(298,15), ккал/моль, считанные из JANNAF.
таблицы на 200, 298,15,300,400,500,....,6000 К.
таблицы на 200, 298,15,300,400,500,....,6000 К.
Строки 8-13 представляют собой значения H-H(298,15), ккал/моль, считанные из JANNAF.
таблицы на 200, 298,15,300,400,500,....,6000 К.
STANJAN уже включает газообразные соединения, с которыми вы обычно сталкиваетесь в большинстве реакций горения, то есть содержащие C, H, N и O. Этого будет достаточно для расчетов с большинством жидких топлив. Однако, если вы планируете выполнять расчеты с участием твердого топлива, в выхлоп будут введены новые элементы, такие как Al и Cl. Это потребует создания совершенно новой группы файлов данных о видах. NIST Chemistry WebBook позволяет выбирать данные либо в калориях, либо в джоулях. Термохимические таблицы NIST-JANAF хоть и представляет данные в более удобном формате, но необходимо перевести из джоулей в калории, где 1 калория = 4,184 джоуля.
NIST Chemistry WebBook позволяет выбирать данные либо в калориях, либо в джоулях. Термохимические таблицы NIST-JANAF хоть и представляет данные в более удобном формате, но необходимо перевести из джоулей в калории, где 1 калория = 4,184 джоуля.
CH6N2 1951 46.
 07170 12.940 0.866 1C 6H 2N 0 0 0
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
07170 12.940 0.866 1C 6H 2N 0 0 0
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
.000 .000 .000 .000 .000 .000 .000 .000 .000 .000
Конечно, поначалу кажется, что температура 298,15 К может быть проблемой при использовании криогенного топлива, но есть способ обойти это. Кроме того, STANJAN допускает минимальную начальную температуру 200 К, поэтому мы не можем настроить наши реагенты на криогенные температуры, даже если бы захотели. Кроме того, STANJAN не допускает реагентов с разными температурами, поэтому он не может справиться с такими сценариями, как RP-1 и LOX, где температуры сильно различаются.
Кроме того, STANJAN не допускает реагентов с разными температурами, поэтому он не может справиться с такими сценариями, как RP-1 и LOX, где температуры сильно различаются.
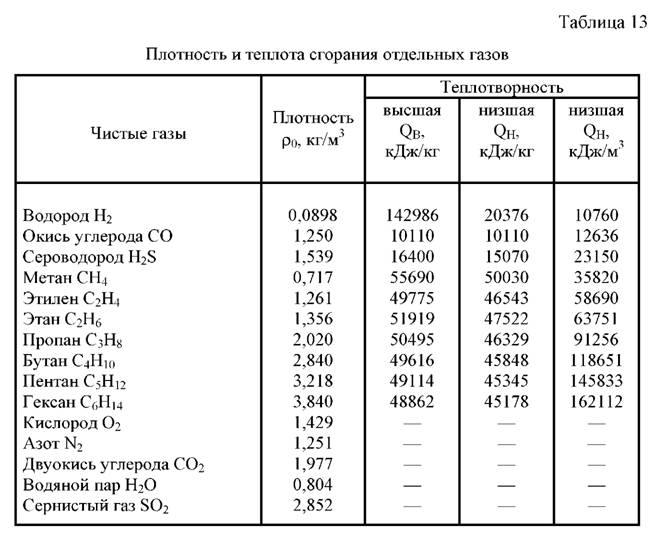 ru: главная страница / / Техническая информация/ / Физический справочник/ / Тепловые величины, включая температуры кипения, плавления, пламени и т.д ……
ru: главная страница / / Техническая информация/ / Физический справочник/ / Тепловые величины, включая температуры кипения, плавления, пламени и т.д ……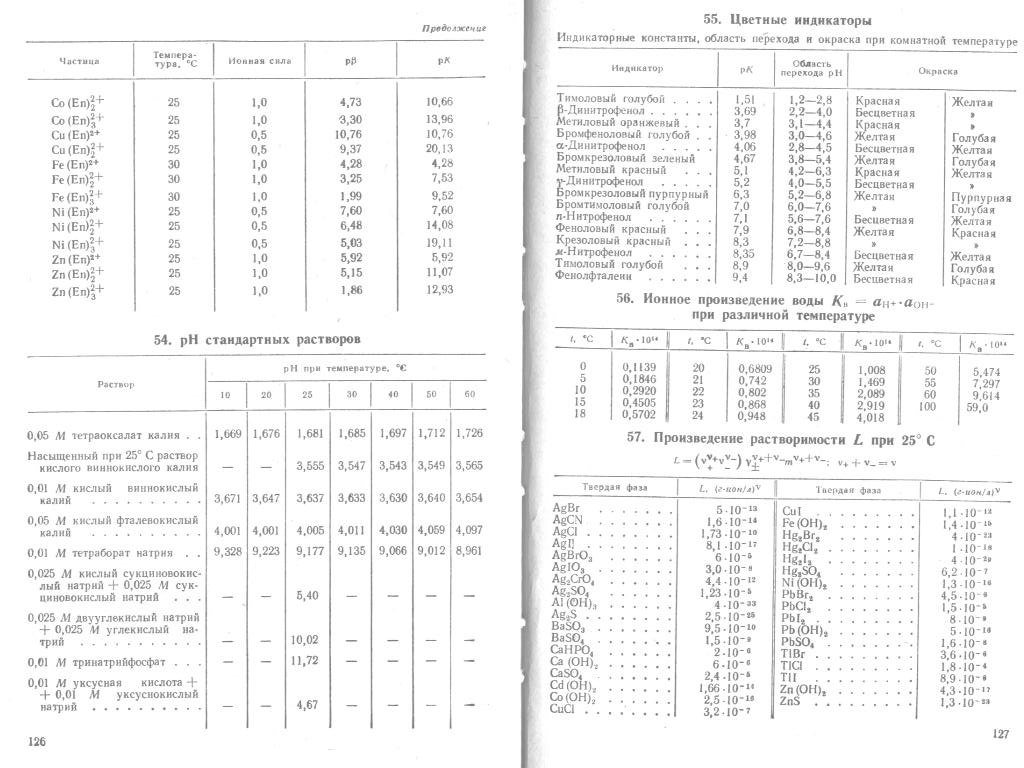 597
597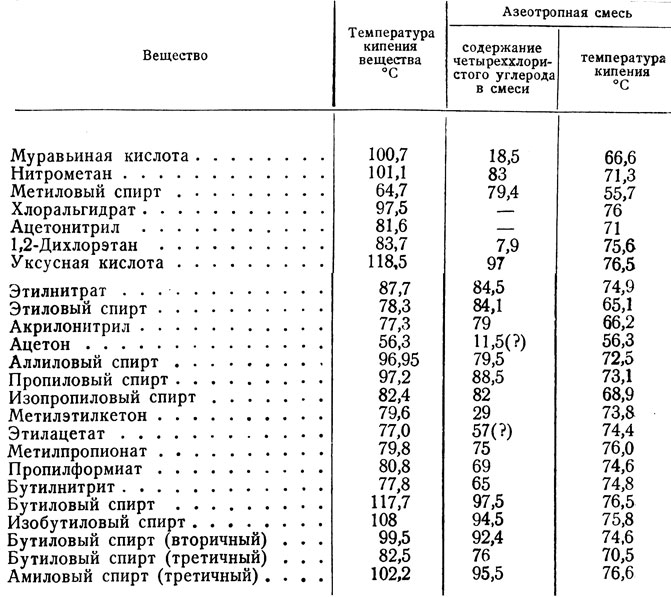 330
330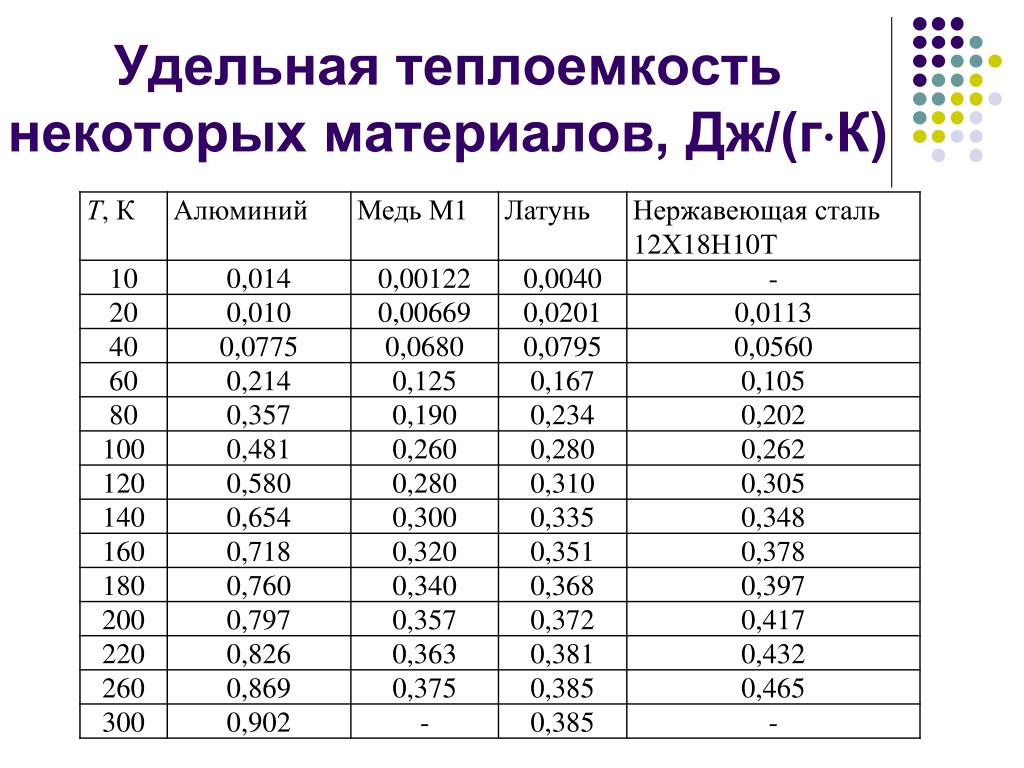 393
393 450
450 404
404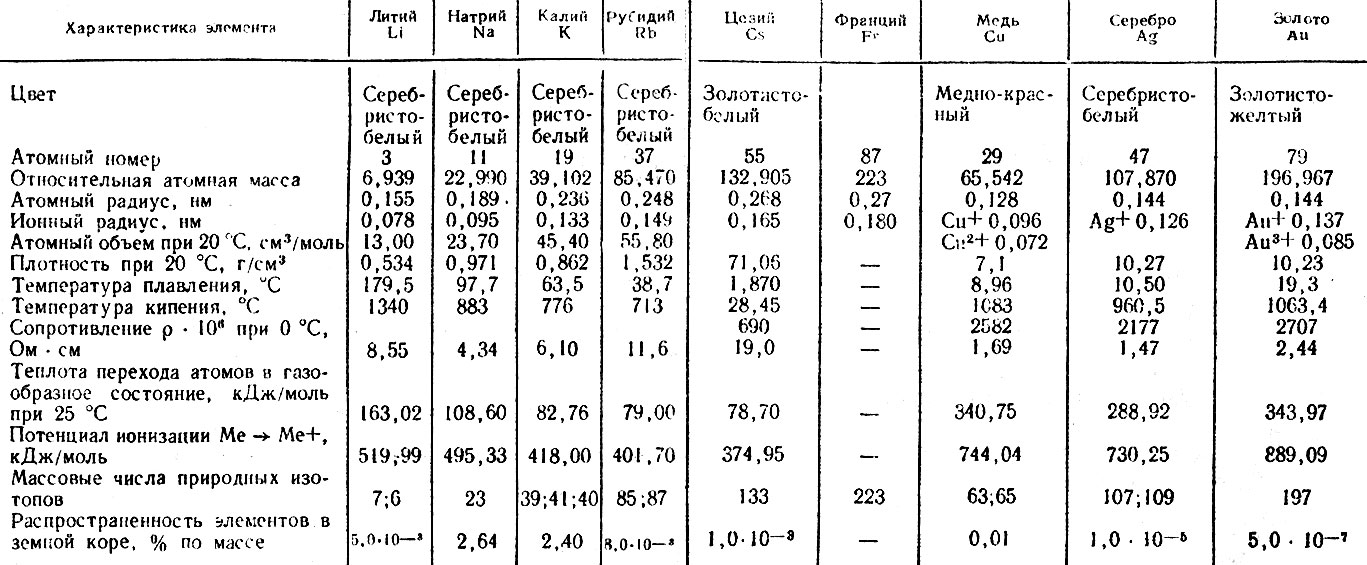 660
660 ru:
ru: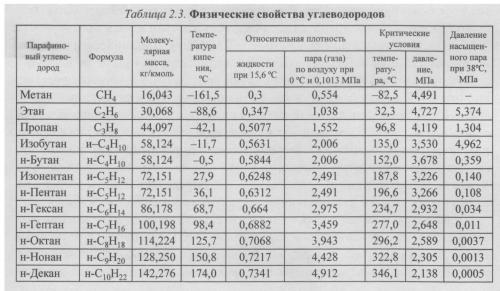 104
104
 ru: главная страница / / Техническая информация/ / Физический справочник / / Тепловые величины: теплоемкость, теплопроводность, температуры кипения, плавления, пламени. Удельные теплоты сгорания и парообразования. Термические константы. Коэффициенты теплообмнена и расширения/ / Температуры, кипения, плавления, прочие… Перевод единиц измерения температуры. Воспламеняемость. / / Температура продуктов сгорания, выходящих газов, температура выхлопных газов, температура выпуска, вытяжная температура, температура выхлопа, температура выхлопных газов, температура отходящих газов – различные процессы, природный газ, сжиженный газ…
ru: главная страница / / Техническая информация/ / Физический справочник / / Тепловые величины: теплоемкость, теплопроводность, температуры кипения, плавления, пламени. Удельные теплоты сгорания и парообразования. Термические константы. Коэффициенты теплообмнена и расширения/ / Температуры, кипения, плавления, прочие… Перевод единиц измерения температуры. Воспламеняемость. / / Температура продуктов сгорания, выходящих газов, температура выхлопных газов, температура выпуска, вытяжная температура, температура выхлопа, температура выхлопных газов, температура отходящих газов – различные процессы, природный газ, сжиженный газ… д…
д…
 000 Btu/h
000 Btu/h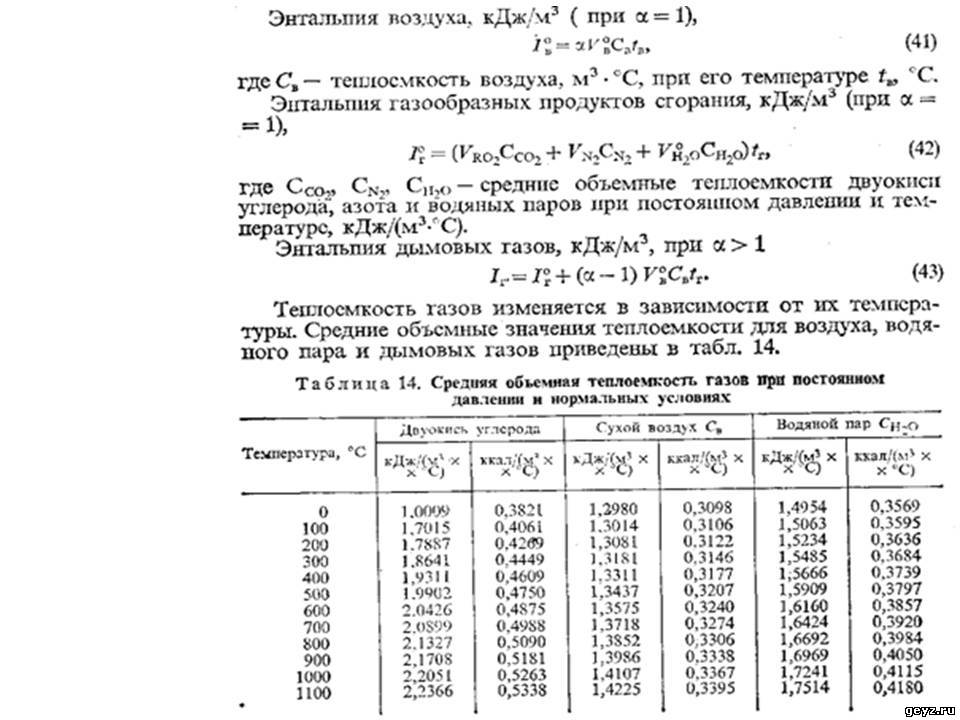 Введите свой запрос:
Введите свой запрос: