Физические свойства воздуха :: HighExpert.RU
Воздух – это смесь различных газов (% по объему): азот — 78,03; кислород — 20,95; озон и другие инертные газы: аргон, гелий, неон, криптон, ксенон, радон — 0,94; углекислый газ — 0,03; водяной пар — 0,05. Содержание углекислого газа в атмосферном воздухе принимается равным (% по объему): в сельской местности — 0,03, в городах — 0,04—0,07. Содержание водяных паров в воздухе зависит от его температуры. Озон присутствует в лесном, горном и морском воздухе. Наружный воздух загрязняется отходящими от промышленных предприятий вредными для здоровья человека газами и пылью.
Плотность воздуха при нормальном атмосферном давлении 101,325 кПа (1 атм) и различной температуре
| Температура воздуха | Плотность воздуха, ρ |
| оС | кг/м3 |
| -20 | 1,395 |
| 0 | 1,293 |
| 5 | 1,269 |
| 10 | 1,247 |
| 15 | 1,225 |
| 1,204 | |
| 25 | 1,184 |
| 30 | 1,165 |
| 40 | 1,127 |
| 50 | 1,109 |
| 60 | 1,060 |
| 70 | 1,029 |
| 80 | 0,9996 |
| 90 | 0,9721 |
| 100 | 0,9461 |
Динамическая и кинематическая вязкость воздуха при нормальном атмосферном давлении и различной температуре
| Температура воздуха | Динамическая вязкость воздуха, μ | Кинематическая вязкость воздуха, ν |
| оС | (Н • c / м2) x 10-5 | (м2 / с) x 10-5 |
| -20 | 1,63 | 1,17 |
| 0 | 1,71 | 1,32 |
| 5 | 1,73 | 1,36 |
| 10 | 1,76 | 1,41 |
| 15 | 1,80 | 1,47 |
| 20 | 1,82 | 1,51 |
| 25 | 1,85 | 1,56 |
| 30 | 1,86 | 1,60 |
| 40 | 1,87 | 1,66 |
| 50 | 1,95 | 1,76 |
| 60 | 1,97 | 1,86 |
| 70 | 2,03 | 1,97 |
| 80 | 2,07 | 2,07 |
| 90 | 2,14 | 2,20 |
| 100 | 2,17 | 2,29 |
Основные физические своqства воздуха при различной температуре
| Температура | Плотность, ρ | Удельная теплоёмкость, Cp | Теплопроводность, λ | Кинематическая вязкость, ν | Коэффициент температурного линейного расширения, α | Число Прандтля, Pr |
| оС | кг/м3 | кДж / (кг • К) | Вт / (м • К) | (1 / K) x 10-3 | – | |
| 0 | 1,293 | 1,005 | 0,0243 | 13,30 | 3,67 | 0,715 |
| 20 | 1,205 | 1,005 | 0,0257 | 15,11 | 3,43 | 0,713 |
| 40 | 1,127 | 1,005 | 0,0271 | 16,97 | 3,20 | 0,711 |
| 60 | 1,067 | 1,009 | 0,0285 | 18,90 | 3,00 | 0,709 |
| 80 | 1,000 | 1,009 | 0,0299 | 20,94 | 2,83 | 0,708 |
| 100 | 0,946 | 1,009 | 0,0314 | 23,06 | 2,68 | 0,703 |
Формулы физических свойств воздуха
При проведении инженерных расчетов удобнее использовать приближённые формулы для определения физических свойств воздуха⋆:
Плотность воздуха
[ кг/м3 ]Теплоёмкость воздуха
⋆ [ Дж/(кг • К) ]Теплопроводность воздуха
⋆ [ Вт/(м • K) ]Динамическая вязкость воздуха
⋆ [ Па • c ]Кинематическая вязкость воздуха
[ м2/с ]Температуропроводность воздуха
⋆ [ м2/с ]Число Прандтля воздуха
[ – ]⋆ Приближённые формулы физических свойств воздуха получены авторами настоящего сайта.
Размерность величин: температура – К (Кельвин).
Приближённые формулы действительны в диапазоне температур воздуха от 273 К до 473 К.
17.06.2021
Объемная теплоемкость газа – Энциклопедия по машиностроению XXL
Уравнения для средних массовых и объемных теплоемкостей газов в пределах от О до 1 500 С приведены в табл. XIV приложения. В будущем при издании достаточно большого числа пособий, в которых будут приведены точные значения теплоемкостей, а также энтальпии и внутренней энергии, расчет теплоемкостей по приближенным эмпирическим формулам потеряет всякий смысл.Средняя объемная теплоемкость газов [c.542]
Таким образом, объемная теплоемкость смеси равна сумме произведений объемных теплоемкостей газов, входящих в смесь, на их объемные доли. [c.
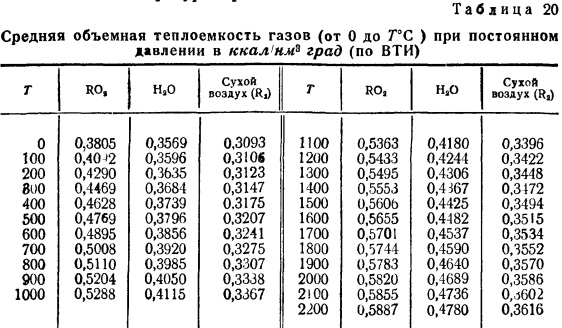136]Задача 2.10. В топке котельного агрегата сжигается карагандинский уголь марки К состава ” = 54,7% Н = 3,3% Sp = 0,8% N = 0,8% 0 = 4,8% ” = 27,6% ” = 8,0%. Определить потери теплоты с уходящими газами из котлоагрегата, если известны коэффициент избытка воздуха за кот л о агрегатом Оу,= 1,43, объем уходящих газов на выходе из последнего газохода Fyi = 8,62 м /кг, температура уходящих газов на выходе из последнего газохода 150°С, средняя объемная теплоемкость газов при постоянном давлении с,у,= 1,4 кДж/(м К), температура [c.40]
Задача 2.12. Определить, на сколько процентов возрастут потери теплоты с уходящими газами из котельного агрегата при повышении температуры уходящих газов ву, со 160 до 180°С, если известны коэффициент избытка воздуха за котлоагрегатом Оу,= 1,48, объем уходящих газов на выходе из последнего газохода Vy = 4,6 м /кг, средняя объемная теплоемкость газов при постоянном давлении Сру = 1,415 кДж/(м К), теоретический объем воздуха, необходимый для сгорания 1 кг топлива V° = 2,5 м /кг, температура воздуха в котельной /, = 30°С, средняя объемная теплоемкость воздуха при постоянном давлении Ср,= = 1,297 кДж/(м К) и потери теплоты от механической неполноты сгорания топлива 4 = 340 кДж/кг.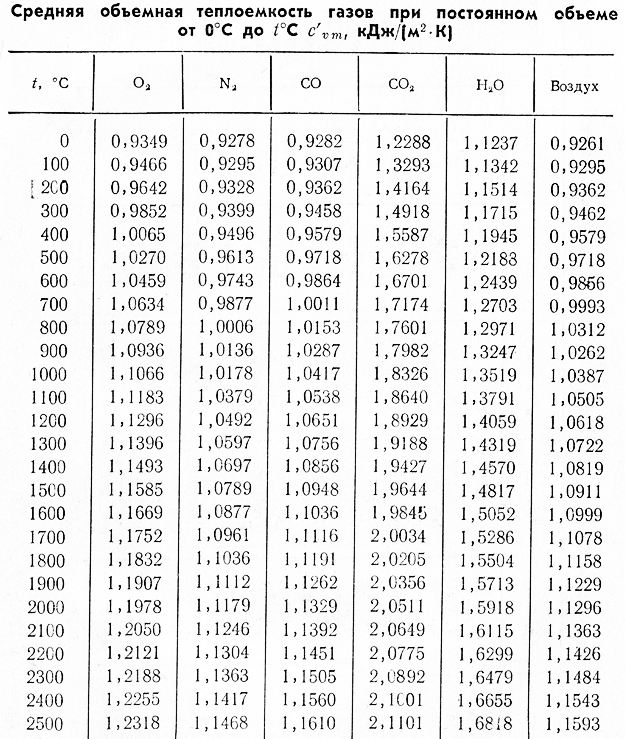
Задача 5.41. Восьмицилиндровый четырехтактный дизельный двигатель эффективной мощностью N =176 кВт работает на топливе с низшей теплотой сгорания 2 S = 42 600 кДж/кг при эффективном кпд je=0,38. Определить в процентах теплоту, превращенную в полезную работу, потери теплоты с охлаждающей водой и потери теплоты с отработанными газами, если расход охлаждающей воды через двигатель 0 = 2 кг/с, разность температур выходящей из двигателя и входящей воды А/ = 10°С, объем газов, получаемый при сгорании 1 кг топлива, Fr=16,4 м /кг, объем воздуха, необходимый для сгорания 1 кг топлива, Кв=15,5 м /кг, температура отработавших газов г = 550°С, средняя объемная теплоемкость газов = 1,44 кДж/(м К) и температура воздуха — [c.174]
Задача 9.2. Определить количество теплоты, отдаваемое уходящими газами котельной спиртового завода водяному экономайзеру (утилизатору), для получения горячей воды, если температура газов на входе в экономайзер 0 = 34О°С, температура газов на выходе из экономайзера 0 = 2ОО°С, теоретический объем газов Fr= 11,48 м /кг, теоретически необходимый объем воздуха И =10,62 м /кг, коэффициент избытка воздуха за экономайзером Оу=1,4, средняя объемная теплоемкость газов = = 1,415 кДж/(м К) и расчетный расход топлива одного котлоагрегата Вр = 0,2 кг/с.
Средняя объемная теплоемкость газов при постоянном давлении (нелинейная зависимость) [c.47]
Объемные теплоемкости газа относятся обычно к объему газа, приведенному к нормальному состоянию, т. е. к 0 С и 760 мм рт. ст.
ОБЪЕМНАЯ ТЕПЛОЕМКОСТЬ ГАЗА [c.49]
Средняя объемная теплоемкость газов при постоянном давлении t, [c.48]
Различия, и существенные, возникают в методике эксперимента, так как вследствие низкой теплопроводности паров и газов происходит значительное перераспределение роли поправок в расчетных формулах (4-60), (4-61). Так, рост допустимых перепадов температуры в рабочем слое влечет за собой некоторое снижение роли поправок Д д о, Дто на паразитные сигналы в термопарах, но зато ощутимо возрастают поправки на нелинейность и Ао , особенно последняя из них.
Низкая теплопроводность и высокая прозрачность газов и паров влекут за собой увеличение роли поправки на излучение и на паразитные тепловые мостики в слое. Благодаря низкой объемной теплоемкости газов и паров резко, практически до пренебрежимых значений, снижаются поправки на теплоемкость и кривизну АОф слоя.
[c.138]
М, Су, Су — молекулярный вес, молекулярная й удельная объемная теплоемкость газа а — коэффициент аккомодации. [c.159]
Средняя объемная теплоемкость газов при t = 1000 С [c.127]
Сг — средняя объемная теплоемкость газов, кДж/(м -К) при tys [c.131]
Больцмана В — расход топлива, кг/с или м /с у — удельный обьем продуктов сгорания, м /кг или м /м с — средняя объемная теплоемкость газов, кДж/(м К) — площадь поверхности материала, через который осуществляется внешний теплообмен, м2 и — степени черноты газов и материала — температура поверхности материала,
[c.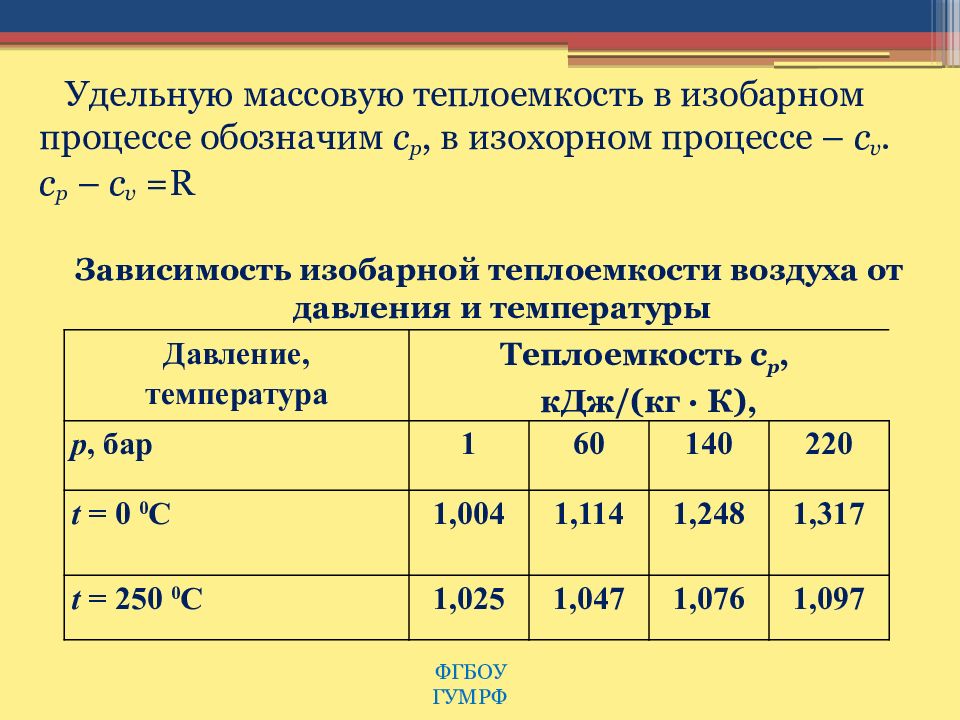
71]
Аналогично плотности и вязкости малые по сравнению с жидкостью теплопроводность и объемная теплоемкость газа (Яд [c.266]
Теория метода для датчика в форме цилиндра является более сложной, чем для датчика — фольги, так как в общем случае результат зависит не от одной переменной Ь, как при плоском слое, а от двух — от 6 и от температуропроводности а. Чтобы получить из экспериментальных данных значения коэффициента теплопроводности, в рассматриваемой работе измерения проведены при постоянном отношении pQ pQ, где с ро — объемная теплоемкость газа, а Срр — датчика. Это делало необходимым при каждой температуре специально подбирать давление газа для выполнения данного условия. [c.36]
Однако 1 л газа можно представить себе существующим при разных давлениях и температурах и, следовательно, имеющим разные массы.
Поэтому условились 1 ж газа брать при нормальных условиях (р = 101325 н/>г = 1,013 бар и = 0° С). Отсюда следует, что единица удельной объемной теплоемкости газа [кдж/(м -град)] относится к массе газа, заключенной в I ж при нормальных условиях.
[c.117]
Средняя мольная теплоемкость обозначается цс (где х—масса моля, кг). Средняя объемная теплоемкость газа при нормальных условиях [c.118]
ИвтерполАЦИот1ые формулы для средних массовых и объемных теплоемкостей газов [c.41]
Задача 2.11. В топке котельного агрегата сжигается каменный уголь с низшей теплотой сгорания Ql = 21 600 кДж/кг. Определить потери теплоты в процентах с уходящими газами из котлоагрегата, если известны коэффициент избытка воздуха за котлоагрегатом Oyj=l,4, объем уходящих газов на выходе из последнего газохода Ку =10,5 м /кг, температура уходящих газов на выходе из последнего газохода 0ух= 160°С, средняя объемная теплоемкость газов при p = onst 1,415 кДж/(м К), теоретический объем воздуха, необходимый для сгорания 1 кг топлива F° = 7,2 м /кг, температура воздуха в котельной /> = 30 С, температура воздуха, поступающего в топку, С = 180°С, коэффициент избытка воздуха в топке се = 1,2, средняя объемная теплоемкость воздуха при постоянном давлении = = 1,297 кДж/(м К) и потери теплоты от механической неполноты сгорания топлива q = A%.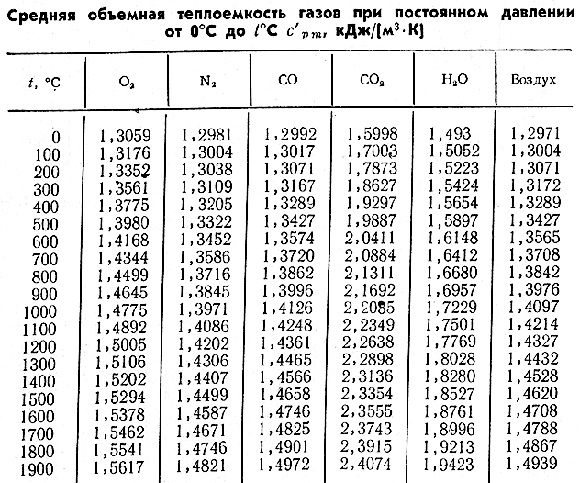
[c.41]
Теплоемкость, отнесенная к 1 молю вещества, называется мольной теплоемкостью цс ккалЫоль град, отнесенная к 1 кГ вещества — весовой теплоемкостью с [ккал кГ град], отнесенная к 1 нм — объемной теплоемкостью С или с [ккал/нм ерад]. Объемные теплоемкости газа относятся обычно к объему газа, приведенному к нормальному состоянию, т. е. к 0 С и 760 мм рт. ст. [c.19]
Постановка и решение задачи могут быть упрощены. Вследствие малой объемной теплоемкости газа в сравнении с теплоемкостью обтекаемой им стенки газ обладает малой тепловой инерцией. За одинаковые промежутки времени стенка и газ будут обмениваться одинаковыми количествами тепла газ будет отдавать тепло, стенка его принимать. Отдача тепла должна компенси- [c.336]
Термобаллоны с короткими капиллярами и с устройствами дистанционной передачи показаний часто применяются в системах управления. Эта аппаратура проста в наладке и обслуживании и избавляет от необходимости введения коррекции на изменение температуры в длинных капиллярах.
В комплекте с короткими капиллярными трубками могут применяться небольшие термобаллоны, заполненные гелием. об.пап.ающие в 2 раза более высоким быстродействием, чем термобаллоны заполненные ртутью. Низкая теплопроводносгь газа не вызывает увеличения постоянной времени, так как объемная теплоемкость газа мала. (Коэффициент температуропроводности к/рСр для гелия при давлении 10 ат в 4 раза превышает соответствующий коэффициент для ртути.)
[c.315]
| | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация / / Свойства рабочих сред / / Воздух (Атмосфера) / / Температура, плотность, удельная теплоемкость, объемный коэффициент теплового расширения, кинематическая вязкость,и число (критерий) Прандтля для сухого воздуха при атмосферном давлении в в диапазоне -150 /+400 oC.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
793
293
711
703
85
0421
068Теплоемкость сухого воздуха – Справочник химика 21
Для тепловых расчетов вводится понятие теплоемкости влажного воздуха С. Величина С определяется как сумма теплоемкостей 1 кг сухого воздуха и X кг водяного пара, которые приходятся на 1 кг сухого воздуха. Так как теплоемкость сухого воздуха равна 0,24 ккал кг град), а теплоемкость водяного пара близка к 0,45 ккал кг град), то теплоемкость влажного воздуха можно, определить по формуле [c.597]Аналитическими исследованиями было установлено, что в отдельных случаях расход тепла на испарение впрыскиваемой воды превышает теплоемкость сухого воздуха в 5—10 раз [80]. [c.141]
При определении показателя политропы т по формуле (VI.27) условно принимается, что впрыскиваемая вода в потоке воздуха испаряется полностью, а теплоемкость паровоздушной смеси Срт равна теплоемкости сухого воздуха, что не соответствует реальным условиям испарительного охлаждения впрыскиваемая вода в потоке воздуха испаряется не полностью, а теплоемкость паровоздушной смеси в адиабатическом процессе сжатия меняется.
[c.140]
Теплоемкость паровоздушной смеси при испарительном охлаждении возрастает и значительно превышает теплоемкость сухого воздуха. [c.174]
Здесь Се в =1.01 кДж/(кг-К)—средняя удельная теплоемкость сухого воздуха при постоянном давлении I — Температура воздуха, Х п — удельная энтальпия перегретого пара, кДж/кг с = 1,97 кДж/(кг-К) — средняя удельная теплоемкость водяного пара го = 2493 к-Дж/кг — удельная теплота парообразования воды при О С. [c.282]
При вычислении теплоемкости сухого воздуха принимается следующий его объемный состав [Л. 2] [c.87]
Теплоемкость паровоздушной смеси при испарительном охлаждении водой оказалась в 2,33 раза больше теплоемкости сухого воздуха. [c.175]
В развернутом виде, принимая теплоемкость сухого воздуха постоянной и равной 1010 Дж/кг-град и водяного пара 1970 Дж/кг град, получим теплосодержание влажного воздуха [c.
197]
Теплоемкости сухого воздуха и паров увлажняющих жидкостей в интервале средних температур процессов сжатия и расширения [c.248]
Для температуры и давлений, применяемых в сушильной технике, приблизительно можно считать теплоемкость сухого воздуха кДж/(кг К), а для водяного перегретого пара Лп= г = Срп( = (2500 + 1,960 кДж/кг. Тогда [c.101]
В каждом случае коэффициент следует умножить на плотность или удельную теплоемкость сухого воздуха при температуре и давлении смеси. [c.197]
При этом с приближением, обеспечивающим достаточную точность, принимают удельную теплоемкость сухого воздуха [c.65]
Средняя теплоемкость сухого воздуха при О—80°С 1 (0,24), а водяного пара 0,467 (1,97) кДж/(кг-К) [ккал/(кг-К)]. Для [c.209]
В вышеприведенных формулах Р — поверхность теплообмен-ного элемента, м к — начальная и конечная температура воды в пенном аппарате, °С н, — то же охлаждающей воды L — расход воды, подаваемой на решетку пенного аппарата, кг/ч с — теплоемкость воды, кДж/(кг-°С) конечная температура воды, подаваемой на решетку, °С Уг — расход сухого воздуха, м /ч Ср — теплоемкость сухого воздуха, кДж/(м °С) г.
Н1 г. к — температура воздуха на входе и выходе из аппарата, °С /п — энтальпия пара, к Дж/кг Сц и 6п. к — расход водяВо го пара во входящем и выходящем воздухе, кг/ч 0 — потери теплоты в окружающую среду, кДж/г — расход воды в холодильнике, кг/ч а н и в. к— температура воды на входе и выходе из холодильника. [c.113]
Удельные теплоемкости сухого воздуха Ссв и пара в обычном для вентиляционного процесса диапазоне температур можно считать постоянными и равными [c.27]
J – теплоемкость сухого воздуха в ккал/кг °С, [c.396]
В тех интервалах температур, которые в больщинстве случае имеют место при сушке, без большой погрешности можно принимать, теплоемкость сухого воздуха при постоянном давлении [c.397]
Теплосодержание влажного воздуха равно сумме теплосодержаний сухого воздуха i e =0,24i (где 0,24 ккал/кгс-град — удельная теплоемкость сухого воздуха) и водяного пара 4 = = 595+ 0,47i (где 595 ккал/кгс — теплосодержание водяного пара при О (I, а 0.
47 ккал/кгс теплоемкостЬ- пара). Отсю.да т Д-. [c.312]
Сс — удельная теплоемкость сухого воздуха, равная 1 кДж/(кг-К) [c.186]
Здесь с, я Си — соответственно теплоемкости сухого воздуха и водяного пара, Дж/(кг-К) /1 —показания термометра перед сушилкой. [c.216]
Подставив значение / в выражение (21-7) и принимая удельную теплоемкость сухого воздуха постоянной (1000 дж1кг-град), найдем энтальпию влажного воздуха (в дж1кг сухого воздуха) [c.738]
Примечания. I. В формулах расчета прихода тепла величины 0,13 и 1 —удельные теплоемкости сухого воздуха и водяного пара, ккалЦмЗ-грай) (см. Приложение XVIII) значе-2. В формулах расчета расхода тепла величина 0.19—теплоемкость огарка, ккал/[кг-град). газа, ккал/ .ч -град), найдена по данным Приложения Х И. [c.106]
Примечания. 1. В формулах расчета прихода тепла величины 0,13 и 1 —удельные теплоемкости колчедана и воды, ккал/(кг- С) величины 0,31 и 0,36 — средние объемные теплоемкости сухого воздуха и водяного пара, ккал/(мЗ-°С), см.
Приложение ХУП1. Значение ( 5 определено по уравнениям (3-12) и (3-13) с учетом уравнения (3-31) и данных табл. 3-5. [c.87]
ОПРЕДЕЛЕНИЕ ТЕПЛОЕМКОСТИ ВОЗДУХА – PDF Free Download
ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ВЛАЖНОГО ВОЗДУХА
Министерство образования и науки РФ Федеральное агентство о образованию Саратовский государственный технический университет ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ВЛАЖНОГО ВОЗДУХА Методические указания к лабораторной
ПодробнееОПРЕДЕЛЕНИЕ ТЕПЛОЕМКОСТИ ТВЕРДЫХ ТЕЛ
Лабораторная работа 6 ОПРЕДЕЛЕНИЕ ТЕПЛОЕМКОСТИ ТВЕРДЫХ ТЕЛ Цель работы определение теплоемкости образцов металлов калориметрическим методом с использованием электрического нагрева.
Из теории идеального
5 ТЕПЛОЕМКОСТЬ ГАЗОВ
3 СОДЕРЖАНИЕ Введение 4 Параметры состояния тела 5. Удельный объем и плотность 5. Давление 5.3 Температура 6 Идеальный газ, уравнение состояния идеального газа 7 3 Газовые смеси 9 3. Понятие о газовой
ПодробнееЛабораторная работа 5
Мордовский государственный университет имени Н.П.Огарева Институт механики и энергетики Кафедра теплоэнергетических систем Методические указания к лабораторным работам по курсу “Теоретические основы теплотехники”
ПодробнееВиртуальная лабораторная работа 6
Виртуальная лабораторная работа 6 ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ МОЛЯРНЫХ ТЕПЛОЕМКОСТЕЙ C /C v ДЛЯ ВОЗДУХА (компьютерное моделирование) В.В.Монахов, А.В.Кожедуб, А.В.Смирнов Цель работы – экспериментальное определение
ПодробнееЛАБОРАТОРНАЯ РАБОТА 5.
4. Q=2prhq =-2p rhc dt dr. (1)ЛАБОРАТОРНАЯ РАБОТА 5.4 ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ ВОЗДУХА Цель работы: экспериментальное определение коэффициента теплопроводности воздуха. Литература: [4] гл. 5 5.1, 5.2, 5.5; [7] гл.
ПодробнееПРОВЕРКА ЗАКОНА ДЖОУЛЯ-ЛЕНЦА
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «Оренбургский государственный
ПодробнееЛабораторные работы.
Лабораторные работы. Лабораторная работа 1. Сравнение количеств теплоты при смешивании воды разной температуры. Цель работы: определить количество теплоты, отданное горячей водой и полученное холодной
ПодробнееЛабораторная работа 2
КАЛМЫЦКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Кафедра общей физики Лабораторная работа 2 «Определение удельной теплоемкости жидкости» Лаборатория 2 Лабораторная работа 2 «Определение удельной теплоемкости жидкости»
ПодробнееСхема экспериментальной установки
Работа 2.
2 ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ ГАЗА МЕТОДОМ АДИАБАТИЧЕСКОГО РАСШИРЕНИЯ Цель работы: ) изучение первого начала термодинамики в различных изопроцессах; 2) экспериментальное определение показателя
Лабораторная работа 8. Краткая теория
Лабораторная работа 8 Определение отношения теплоемкости газа при постоянном давлении к теплоемкости газа при постоянном объеме Цель работы: изучение законов идеального газа и определение опытным путем
ПодробнееЛабораторная работа 9
КАЛМЫЦКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Кафедра общей физики Лабораторная работа 9 «Определение теплоты перехода воды в пар при температуре кипения» Лаборатория 211 Лабораторная работа 9 «Определение теплоты
ПодробнееСоставитель Н.С. Кравченко, Н.И.Гаврилина
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» УТВЕРЖДАЮ Проректор-директор
ПодробнееИЗУЧЕНИЕ РЕАЛЬНОГО ГАЗА
Цель работы.
Лабораторная работа 4 ИЗУЧЕНИЕ РЕАЛЬНОГО ГАЗА (Эффект Джоуля-Томсона) Целью лабораторной работы является экспериментальное определение изменения температуры воздуха в процессе адиабатного
Определение объёмной изобарной теплоёмкости воздуха
Цель работы: экспериментальное определение средней объёмной изобарной теплоёмкости воздуха ср‘ (Дж/кг·К) в интервале температур от комнатной 200C до 800С, построение графика зависимости теплоёмкости от температуры, а также вычисление энтальпии газа.
Краткие теоретические сведения
Удельная теплоёмкость является термодинамическим параметром вещества и соответствует количеству теплоты, которое необходимо сообщить единице количества вещества для повышения его температуры на 1 градус. В зависимости от количественной меры вещества различают удельные теплоёмкости: массовую с [Дж/кг·К], объёмную сʹ [Дж/м3·К] и молярную сμ [Дж/моль·К].
Теплоёмкость зависит также и от процесса изменения состояния газа и температуры. Различают теплоёмкость при постоянном давлении ср (изобарная теплоёмкость) и при постоянном объёме сv (изохорная теплоёмкость). Для идеальных газов взаимосвязь между ними определяется уравнением Майера:
ср – сv = R. (3.1)
В реальных газах при расширении совершается не только внешняя, но и внутренняя работа, вызванная изменением внутренней потенциальной энергии газов, поэтому разность теплоемкостей оказывается больше значения их газовой постоянной R:
ср – сv > R. (3.2)
Существует понятие истинной теплоемкости, при конкретной температуре t, представляющее собой отношение элементарного количества тепла, сообщенного газу к бесконечно малой разности изменения температуры газа в этом процессе , и средней теплоемкости, т.е. отношения конкретного количества тепла q1-2, переданного газу в процессе 1-2, к конечной разности температур t1– t2
= .
(3.3)
Удельной объёмной изобарной теплоёмкостью является количество теплоты, необходимое для нагревания 1 м3 газа на 1 градус в изобарном процессе. В 1м3 в зависимости от температуры и давления может содержаться различное по массе количество газа. Поэтому удельную объёмную теплоёмкость принято приводить к нормальным условиям, т.е. к давлению 101 325 Па и температуре 273,15 К (р = 760 мм рт. ст. и t = 00C). Единица удельной объёмной теплоёмкости – джоуль на кубический метр – кельвин [Дж/м3·К].
Описание экспериментальной установки
Рабочим участком лабораторной установки (рис. 3.1.) является проточный калориметр 2.
Рис. 3.1. Схема лабораторной установки для определения объёмной изобарной теплоёмкости воздуха
1 – вентилятор, 5, 10 – термопары, 9 – амперметр, 4 – выключатель, 8 – лабораторный трансформатор, 6- пневматическая трубка 7 – дифференциальный манометр, 4 – вольтметр, 3 – нагреватель, 2 – проточный калориметр.
Корпус калориметра изготовлен из теплоизоляционного материала с внутренним диаметром 1см, внутри которого расположена спираль нагревателя 9.
Напряжение электрического тока, подводимого к нагревателю, измеряется амперметром 3, вольтметром 4 и регулируется лабораторным трансформатором 5.
Нагнетание воздуха через калориметр осуществляется вентилятором 1.Температура воздуха, на входе в нагреватель измеряется термопарой 2, на выходе – термопарой 6; обе термопары подключены к потенциометру.
Расход воздуха через калориметр регулируется мембраной и измеряется на выходе из него с помощью дифференциального манометра 7.
Методика выполнения работы
Перед проведением опытов измерить атмосферное давление В и температуру воздуха в лаборатории tв, записать их значения в протокол наблюдений журнала (Примечание, ) .
Таблица 3.1.
| № опыта | Т1, К | Т2, К | J, А | U, В | Н,
мм в. ст.
| рm, Дж/м3·К | Приме-чание |
| 1,2 |
Подключить установку к электрической сети лаборатории. Включить вентилятор и подогреватель на боковой панели установки. Ручкой трансформатора 5 установить напряжение электрического тока, подводимого к нагревателю, контролируемого по вольтметру, U = 30-50 В. По достижении стационарного режима, о наступлении которого судят по стабилизации показаний термометров, снять показания дифференциального манометра, вольтметра, амперметра и записать их значения для первого режима в протокол наблюдений журнала лабораторных работ.
Провести аналогичные измерения, повышая трансформатором напряжение тока на 20-30В для каждого опыта, добиваясь при этом ожиданием стабилизации теплового режима.
Результаты измерений записать в таблицу протокола наблюдений.
По окончании измерений вращением против часовой стрелки ручки трансформатора установить напряжение, подаваемой на нагреватель равным нулю. После того, как нагреватель охладится ниже 500С выключить его и вентилятор выключателем на боковой панели установки.
Обработка результатов эксперимента
Вначале по показаниям амперметра и вольтметра вычислить количество теплоты, передаваемое в калориметре ежесекундно:
Q = 0,86 I·U, Вт, (3.1)
где I – сила тока, А; U – напряжение на участке нагрева установки, В.
Объёмный расход воздуха, приведённый к нормальным условиям, определяется по следующей формуле:
Vн = (πd 2/ 4)·ωср·(В / 760)·(273 / Та), м3/с, (3.2)
где d – диаметр трубы, м; ωср – средняя скорость воздуха в трубе, м/с;
В – барометрическое давление, мм рт ст.
Величина ωср определяется по осевой скорости ω0 из соотношения
ωср = с·ω0, м/с (3.3)
где с – скоростной коэффициент, определяемый в зависимости от критерия Рейнольдса, по графику (приложение).
Осевая скорость ω0 находится по динамическому напору:
ω0 = (3.4)
где рд – динамический напор, н/м2;
g – ускорение силы тяжести, м/с2;
γв – удельный вес воздуха, н/м3.
Динамический напор вычисляется по формуле:
рд = Н·(γж – γв), н/м2, (3.5)
где Н – высота столба воды, уравновешивающей динамический напор, м;
γж, γв – удельные веса воды и воздуха, н/м3.
Поскольку температурный уровень в калориметре невысок, то тепловыми потерями в нем можно пренебречь, кроме того, можно не учитывать и изменения температуры воздуха и из-за дросселирования, в виду близости свойств воздуха, при атмосферном давлении, свойствам идеального газа.
Поэтому величину средней объёмной изобарной теплоёмкости вычисляем для каждого опыта по следующей формуле:
р = Q / Vн·(t2 – t1). (3.6)
Полученные значения теплоёмкостей занести в журнал и на основании этих данных построить график зависимости теплоёмкости воздуха от температуры, при этом по оси ординат отложить значения средних теплоёмкостей в каждом опыте, а по оси абсцисс значения средних температур потока воздуха , определяемые по формуле:
= (t2 + t1) / 2. (3.7)
Оценка погрешностей измерения.
Относительная погрешность измерения теплоемкости в соответствии с расчетной формулой (3.6) определится выражением:
δ р = + + ,
где относительная погрешность определения переданного тепла определится суммой относительных погрешностей определения тока и напряжения:
= .
Относительная погрешность определения объемного расхода оценивается погрешностью градуировки мерной диафрагмы ≈ 1%, погрешность измерения разности температур оценивается погрешностью градуировки хромель-копелевых термопар ≈ ± 0,6 0С или ·100%.
Контрольные вопросы
1.Дайте определение средней теплоёмкости.
2.Какова зависимость теплоёмкости от температуры?
3.Что такое удельная теплоёмкость и какова ее размерность?
4. Какие соотношения установлены между удельными теплоёмкостями идеальных газов.
5.В чём разница между истинной и средней теплоёмкостью?
6.Как определить среднюю теплоёмкость в интервале температур t1 – t2?
7.Каковы пределы изменения теплоёмкости?
8.Какими приборами определяется расход воздуха в данной установке?
9.От чего зависит теплоемкость идеальных газов?
2.5. Лабораторная работа № 6.
Лабораторная работа №2. ОПРЕДЕЛЕНИЕ СРЕДНЕЙ ИЗОБАРНОЙ ТЕПЛОЁМКОСТИ ВОЗДУХА
ОПРЕДЕЛЕНИЕ СРЕДНЕЙ ИЗОБАРНОЙ ТЕПЛОЁМКОСТИ ВОЗДУХА
1. Цель работы:
а) приобретение навыков экспериментального определения средней объёмной изобарной теплоёмкости воздуха с помощью проточного калориметра;
б) вычисление по измерянным величинам средних объёмной, массовой и мольной изобарной теплоёмкости воздуха;
в) оценка точности экспериментального определения средней изобарной теплоёмкости воздуха.
2. Пояснение к работе
Отношение элементарного количества теплоты dq, подводимого к единице количества вещества в данном термодинамическом процессе, к изменению температуры DТ вещества в этом процессе называется средней теплоёмкостью, то есть
(1)
Предел этого отношения
(2)
является истинной теплоёмкостью в данной точке термодинамического процесса. Это есть математические определения средней и истинной теплоёмкостей.
С физической точки зрения средняя теплоёмкость есть количество теплоты, необходимое для нагрева единицы количества вещества на один градус в данном интервале температур в заданном процессе.
Из совместного рассмотрения этих определений теплоёмкости следует, что, во-первых, теплоёмкость в общем случае есть функция процесса. Однако она становится функцией состояния, когда термодинамический процесс задан. Во-вторых, средняя теплоёмкость в заданном процессе может быть определена экспериментально, а истинная – только рассчитана из соотношения (2).
Количество рабочего тела (вещества) может быть задано в килограммах, киломолях и нормальных кубических метрах. В связи с этим, соответственно различают массовую, мольную и объёмную теплоёмкости, имеющие размерности кДж/(кг×К), кДж/(кмоль×К) и кДж/(нм3×К).
Теплоёмкость реального газа в заданном термодинамическом процессе зависит от двух параметров состояния, и чаще всего её представляют в табличной либо аналитической форме в зависимости от температуры и давления или от температуры и удельного объёма. Для идеального газа теплоёмкость зависит только от температуры: С = f (Т). Наконец, в рамках упрощенной молекулярно-кинетической теории зависимость теплоёмкости от температуры не учитывается, а учитывается только её зависимость от строения молекулы вещества: от числа атомов в молекуле рассматриваемого газа. По этой концепции изобарная и изохорная теплоёмкости рассчитываются из соотношений:
и (3)
где: j – число вращательных внутримолекулярных степеней свободы:
для одноатомных молекул j = 0;
для двухатомных молекул j = 2;
для трёх и более атомных молекул j = 3;
R – газовая постоянная, кДж/(кг×К).
Количество теплоты, подводимое к телу в заданном термодинамическом процессе ( ) при изменении его температуры от t1 до t2, рассчитывается из соотношения
(4)
где Сx – истинная удельная теплоёмкость вещества в заданном процессе при данной температуре;
– средняя удельная теплоёмкость в заданном процессе в интервале температур [t1 , t2].
3. Описание лабораторной установки.
В данной работе определяется изобарная теплоёмкость воздуха, так как в проточном калорифере давление воздуха при его нагреве не меняется.
Принципиальная схема лабораторной установки приведена на рис 2.
Установка для измерения средней теплоёмкости воздуха включает: проточный калорифер – 1, электронагреватель – 2, лабораторный автотрансформатор – 3, электровентилятор – 4, газовый расходомер (счетчик) – 5, вольтметр – 6, амперметр – 7. Кроме того для проведения опытов необходимо иметь барометр для измерения атмосферного давления и секундомер (либо часы с секундной стрелкой) для измерения времени экспозиции.
4. Методика проведения опытов:
4.1. До начала выполнения измерений ознакомьтесь с устройством установки на месте.
4.2. Вначале переведите установку из стационарного холодного состояния в первое нагретое состояние. Для этого, руководствуясь схемой установки, включите установку и, не включая нагреватель, дождитесь постоянства температуры воздуха на выходе из калорифера (t2). Согласуйте показания гальванометра с этой температурой c помощью корректора, имеющегося у гальванометра (t1=t2).
4.3. Подайте при помощи автотрансформатора напряжение на нагреватель в пределах 90 –120 В. Дождитесь нового постоянства температуры воздуха на выходе из калорифера (t2), то есть второго стационарного нагретого состояния установки.
4.4. Измерения можно начинать только тогда, когда температура воздуха на выходе из проточного калориметра (t2) будет изменяться (увеличиваться) не более чем на 0,5 0С в минуту. Это, как правило, наступает при достижении температуры воздуха на выходе из калориметра (t2) примерно 40 0С.
4.5. Для проведения опыта необходимо одновременно измерить значения температур воздуха на входе (t1) и на выходе из калорифера (t2), а также показания газового счетчика (две цифры до запятой и две после). После экспозиции примерно 180 сек. повторить измерения этих параметров.
Результаты измерений записать в таблицу наблюдений (количество опытов согласовать с преподавателем).
Таблица 1
Таблица величин, измеренных в процессе проведения опытов
| №№ опытов | Показания электроприборов | Данные для расчета расхода воздуха | Температура воздуха, 0С | Атмосферное давление | ||||
| напряжение U, B | сила тока I, A | показания газового счетчика | время между замерами t, с | при входе в | при выходе из | Ратм = = мм рт. ст. = Па | ||
| V , м3 | V , м3 | калориметр | Примечание | |||||
| t1 | t2 | |||||||
5. Обработка результатов измерений
5.1 Рассчитываем значение средней объёмной изобарной теплоёмкости воздуха
(5)
где Q = U×I×x×10-3, кВт, то есть (кДж/с) – тепловая нагрузка калорифера в единицу времени;
x = 0,87 – доля теплоты, идущей на нагрев воздуха;
– расход воздуха через калорифер, пересчитанный к нормальным условиям.
Обычно po = 760 мм рт. ст. или 1,01325×105 Па;
tо = 0 оС или То = 273,15 К.
– расход воздуха, уходящего из калорифера при температуре (t2).
5.2 Рассчитываем значение средней массовой изобарной теплоёмкости воздуха
(6)
где коэффициент 22,4 нм3/кмоль – это объём одного киломоля идеального газа при нормальных условиях;
m – относительная молекулярная масса исследуемого газа;
для воздуха m= 28,96 кг/кмоль – кажущаяся молекулярная масса.
5.3 Рассчитываем значение средней мольной изобарной теплоёмкости воздуха
(7)
5.4 Рассчитываем теоретическую (табличную) среднюю мольную изобарную теплоёмкость воздуха в интервале температур проведения опыта
(8)
где – среднее значение температуры воздуха в опыте;
в свою очередь ,
где – значения температуры воздуха при выходе из калориметра в начале и в конце интервала времени выполнения опыта.
5.5. Рассчитываем относительную погрешность определения средней изобарной теплоемкости воздуха в индивидуальном опыте по сравнению с табличным значением ,m , рассчитаннымиз соотношения (8).
(9)
ВНИМАНИЕ!. Перед подстановкой величин в соотношение (9) необходимо их перевести в одинаковые единицы измерения.
В процессе выполнения лабораторной работы учащийся заполняет свой протокол лабораторной работы, заблаговременно подготовленный к началу соответствующих занятий. После окончательного оформления протокола лабораторной работы (выполнения всех предусмотренных расчетов) и проработки соответствующего теоретического материала, студент в индивидуальном порядке защищает работу. Правила защиты и учета результатов защиты в соответствующем модульном контроле уточняются преподавателем конкретно в начале лабораторного практикума.
Контрольные вопросы:
1. Дайте математическое и физическое определения понятиям «истинная и средняя теплоемкости вещества».
2. Значение какой теплоемкости (истинной или средней) можно рассчитать по измеряемым в работе параметрам? Поясните почему.
3. Какие величины, какими приборами и с какой конкретной целью измеряются в работе?
4. Дайте определение понятию «нормальные условия». В каких случаях они используются? Что означает величина с размерностью нм3? Что означают величины 22,4 нм3и 22,4 литра?
5. Дайте определение понятиям функция состояния и функция процесса. Теплоемкость является функцией процесса или функцией состояния?
6. В чем проявляется двойственность физической сущности теплоемкости с точки зрения основных понятий и определений термодинамики?
7. Как соотносятся (связаны) между собой массовая, объемная и мольная теплоемкости? Каковы их размерности в СИ?
8. В чем состоит отличие между понятиями «теплоемкость тела и удельная теплоемкость вещества»? Связаны ли они между собой?
9. Чему равны теплоемкости веществ в изотермическом и адиабатном (изоэнтропном) процессах?
10. Геометрический смысл средне и истинной теплоёмкости в процессе, изображенном в T,s координатах? Два свойства T,s диаграммы?
11. Запишите соотношения, связывающие значения изобарной и изохорной теплоемкостей.
12. От скольких и каких параметров зависят теплоемкости идеального и реального газов? От чего зависят изохорная и изобарная теплоемкости идеального газа по упрощенной МКТ?
13. Запишите соотношения для расчета изохорной и изобарной теплоемкостей идеального газа по упрощенной модели молекулярно-кинетической теории.
14. Выведите (запишите) соотношение для пересчета измеряемого в опыте расхода воздуха в нм3.
15. Как построены таблицы средних значений теплоемкостей идеального газа? Запишите уравнения для расчета теплоты в процессе с использованием средних табличных теплоёмкостей.
16. От скольких и каких параметров состояния зависят теплоемкости реального и идеального газов? От чего зависит теплоемкость идеального газа по упрощенной модели молекулярно-кинетической теории?
Удельная теплоемкость при постоянном давлении и переменной температуре
Удельная теплоемкость (C) – это количество тепла, необходимое для изменения температуры единицы массы вещества на один градус.
- Изобарическая теплоемкость (C p ) используется для воздуха в системе постоянного давления (ΔP = 0).
- I Сохорическая удельная теплоемкость (C v ) используется для воздуха в замкнутой системе постоянного объема , (= изоволюметрической или изометрической ).
Примечание! При нормальном атмосферном давлении 1,013 бар – удельная теплоемкость сухого воздуха – C P и C V – будет изменяться в зависимости от температуры. Это может повлиять на точность расчетов процессов кондиционирования и кондиционирования воздуха. При расчете массового и объемного расхода воздуха в обогреваемых или охлаждаемых системах с высокой точностью – удельную теплоемкость (= теплоемкость) следует скорректировать в соответствии со значениями на рисунках и в таблице ниже или найти с помощью калькулятора.
- Для обычных расчетов – значение удельной теплоемкости c p = 1,0 кДж / кг K (равно кДж / кг o C) или 0,24 Btu (IT) / фунт ° F – обычно достаточно точный
- Для более высокой точности – значение C p = 1,006 кДж / кг K (равно кДж / кг o C) или 0,2403 Btu (IT) / фунт ° F – это better
Онлайн-калькулятор удельной теплоемкости воздуха
Калькулятор, представленный ниже, можно использовать для оценки удельной теплоемкости воздуха при постоянном объеме или постоянном давлении и при заданных температуре и давлении.
Выходная тепловая мощность выражается в кДж / (кмоль * K), кДж / (кг * K), кВтч / (кг * K), ккал / (кг * K), Btu (IT) / (моль * ° R). ) и британских тепловых единиц (IT) / (фунт м * ° R)
См. также другие свойства Air при меняющейся температуре и давлении: Плотность и удельный вес при переменной температуре, Плотность при переменном давлении, Коэффициенты диффузии для Газы в воздухе, число Прандтля, удельная теплоемкость при переменном давлении, теплопроводность, теплопроводность, свойства в условиях равновесия газ-жидкость и теплофизические свойства воздуха при стандартных условиях, а также состав и молекулярная масса,
, а также Удельная теплоемкость аммиака, Бутан, двуокись углерода, окись углерода, этан, этанол, этилен, водород, метан, метанол, азот, кислород, пропан и вода.
Вернуться к началу
Вернуться к началу
Вернуться к началу
Удельная теплоемкость воздуха при 1 бар (= 0,1 мПа = 14,5 psi):
Для полного стола с Isobaric теплоемкость – поворот экрана!
| Температура | Изохорная удельная теплоемкость (Cv) | Изобарическая теплоемкость (Cp) | Cp / Cv | [° F] | [кДж / моль K] | [кДж / кг K] | [кВтч / (кг K)] | [ккал (IT) / (кг K)] | [ккал (IT) / (фунт ° F)] | [кДж / моль K] | [кДж / кг K] | [(кВт ч) / (кг K)] | [ккал (IT) / (кг K)] [BTU (IT) / фунт ° F] | [ккал (IT) / (фунт ° F)] | [-] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 60 | -213 | -352 | 0.03398 | 1,173 | 0,0003258 | 0,2802 | 0,2287 | 0,05506 | 1,901 | 0,000528 | 0,45405 | 0,37071 9011 9011 9011 | 1,621 | 0,37071 | 1,621 | 1,621 | 1,621 | 0,0002919 | 0,2510 | 0,2050 | 0,05599 | 1,933 | 0,000537 | 0,46169 | 0.37695 | 1,839 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 81,61 | -192 | -313 | 0,02172 | 0,7500 | 0,0002083 | 0,1791 | 0,146123 | 0,1791 | 0,1463 | 0,1463 | 0,1463 | | | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 100 | -173 | -280 | 0,02109 | 0,7280 | 0,0002022 | 0,1739 | 0.1420 | 0,03012 | 1,040 | 0,000289 | 0,24833 | 0,20276 | 1,428 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 120 | -153 | -244 | -153 | -244 | 0,02011 | -244 | 1,022 | 0,000283 | 0,24350 | 0,19930 | 1,415 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 140 | -133 | -208 | 0.02081 | 0,7184 | 0,0001996 | 0,1716 | 0,1401 | 0,02937 | 1,014 | 0,000282 | 0,24219 | 0,19774 | | 0,0001992 | 0,1713 | 0,1399 | 0,02928 | 1,011 | 0,000281 | 0,24147 | 0.19716 | 1,410 | | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 180 | -93,2 | -136 | 0,02076 | 0,7166 | 0,0001991 | 0,1712 | 0,1397 | 0,1712 | 0,1397 | 0,029203 | 0,1397 | 0,029203 | | 0,029203 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 200 | -73,2 | -99,7 | 0,02075 | 0,7163 | 0,0001990 | 0,1711 | 0.1397 | 0,02917 | 1,007 | 0,000280 | 0,24052 | 0,19638 | 1,406 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 220 | -53,2 | -63.7 | -53,2-63.7 | 0,02011-63.7 | 0,02011 | -63.7 | 1,006 | 0,000279 | 0,24028 | 0,19618 | 1,404 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 240 | -33,2 | -27.7 | 0,02075 | 0,7164 | 0,0001990 | 0,1711 | 0,1397 | 0,02914 | 1,006 | 0,000279 | 0,24028 | 0,19618 | 0,24028 | 0,19618 | 0,19618 | 0,24028 | 0,19618 | 0,7168 | 0,0001991 | 0,1712 | 0,1398 | 0,02914 | 1,006 | 0,000279 | 0,24028 | 0.19618 | 1,403 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 273,2 | 0,0 | 32,0 | 0,02077 | 0,7171 | 0,0001992 | 0,1713 | 0,1398 | 0,02914 | 1,006 | 0,000279 | 0,24028 | 0,19618 | 1,403 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 280 | 6,9 | 44,3 | 0,02078 | 0,7173 | 0,0001993 | 0,1713 | 0.1399 | 0,02914 | 1,006 | 0,000279 | 0,24028 | 0,19618 | 1,402 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 288,7 | 15,6 | 60,0 | 0,02078 | 0,7175 | 0,0001993 | 0,1714 | 0,1399 | 0,02914 | 1,006 | 0,000279 | 0,24030 | 0,19620 | 1,402 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 300 | 26,9 | 80.3 | 0,02080 | 0,7180 | 0,0001994 | 0,1715 | 0,1400 | 0,02915 | 1,006 | 0,000280 | 0,24036 | 0,19625 | 0,19625 | 0,19625 0,7192 | 0,0001998 | 0,1718 | 0,1403 | 0,02917 | 1,007 | 0,000280 | 0,24052 | 0.19638 | 1,400 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 340 | 66,9 | 152 | 0,02087 | 0,7206 | 0,0002002 | 0,1721 | 0,1405 | 0,02923 0,1405 | 0,02923 | 0,1405 | 0,02923 | 360 | 86,9 | 188 | 0,02092 | 0,7223 | 0,0002006 | 0,1725 | 0.1409 | 0,02926 | 1,010 | 0,000281 | 0,24123 | 0,19696 | 1,398 | 380 | 107 | 224 | 0,02011 | | 0,02011 | 224 | 0,020112 | 0,020112 1,012 | 0,000281 | 0,24171 | 0,19735 | 1,397 | 400 | 127 | 260 | 0.02105 | 0,7266 | 0,0002018 | 0,1735 | 0,1417 | 0,02937 | 1,014 | 0,000282 | 0,24219 | 0,19774 | 0,24219 | 0,19774 | 0,0002062 | 0,1773 | 0,1448 | 0,02983 | 1,030 | 0,000286 | 0,24597 | 0.20083 | 1,387 | 600 | 327 | 620 | 0,02213 | 0,7641 | 0,0002123 | 0,1825 | 0,1490 | 0,1825 | 0,1490 | 0,03044 | 0,1490 | 0,03044 | 0,03044 | 700 | 427 | 800 | 0,02282 | 0,7877 | 0,0002188 | 0,1881 | 0.Снимка 1536 | 0,03114 | 1,075 | 0,000299 | 0,25675 | 0,20963 | 1,365 | 800 | 527 | 980 | 0,02351 | 0,8117 | 0,0002255 | 0,1939 | 0,1583 | 0,03183 | 1,099 | 0,000305 | 0,26249 | 0,21432 | 1,354 | 900 | 627 | 1160 | 0.02415 | 0,8338 | 0,0002316 | 0,1991 | 0,1626 | 0,03247 | 1,121 | 0,000311 | 0,26772 | 0,21858 | 0,26772 | 0,21858 | 11252 | 0,0002421 | 0,2082 | 0,1700 | 0,03356 | 1,159 | 0,000322 | 0,27675 | 0.22596 | 1,329 | 1500 | 1227 | 2240 | 0,02673 | 0,9230 | 0,0002564 | 0,2204 | 0,1800 | 0,2204 | 0,1800 | 0,035029011 | 0,035029011 | 0,03502 | 1900 | 1627 | 2960 | 0,02762 | 0,9535 | 0,0002649 | 0,2277 | 0.1859 | 0,03593 | 1,241 | 0,000345 | 0,29631 | 0,24193 | 1,301 | | ||
Вернуться к началу
Преобразование единиц измерения:
0009Удельная единица измерения тепла [BTU (IT)], градус Цельсия = [° C], градус Фаренгейта = [° F], градус Кельвина = [K], градус ранкин = [° R], джоуль = [Дж], килокалория (международная таблица) = [ккал (IT)], килограмм = [кг], килоджоуль = [кДж], киловатт-час = [кВтч], моль = [моль], фунт = [фунт]
K в единицах измерения можно заменить на ° C, и наоборот.° R в единицах измерения можно заменить на ° F и наоборот.
- 1 БТЕ / (фунт ° F) = 1 БТЕ / (фунт ° R) = 1 ккал (IT) / (кг ° C) = 1 ккал (IT) / (кг K) = 4186,8 Дж / (кг K) ) = 0,81647 ккал (IT) / (фунт ° F) = 1,163×10 -3 кВтч / (кг K)
- 1 Дж / (кг K) = 1 Дж / (кг ° C) = 2,3885×10 -4 ккал (IT) / (кг o C) = 2.3885×10 -4 Btu / (фунт ° F) = 1.9501×10 -4 ккал (IT) / (фунт ° F)
- 1 ккал (IT ) / (кг ° C) = 1 британских тепловых единиц / (фунт ° F) = 4186,8 Дж / (кг K) = 0,81647 ккал (IT) / (фунт ° F) = 1.163×10 -3 кВтч / (кг K)
- 1 ккал (IT) / (фунт ° F) = 1,2248 Btu / (фунт ° F) = 1,2248 ккал (IT) / (кг ° C) = 5127,9 Дж / ( кг K)
- 1 кДж / (кг K) = 1 кДж / (кг ° C) = 1000 Дж / (кг K) = 1000 Дж / (кг ° C) = 0,23885 ккал (IT) / (кг ° C) = 0,23885 Btu / (фунт ° F) = 0,19501 ккал (IT) / (фунт ° F) = 2,7778×10 -4 кВтч / (кг K)
- 1 кВтч / (кг K) = 0,85985 ккал (IT) / (кг ° C) = 0,85985 БТЕ / (фунт ° F) = 3,6 кДж / (кг · K)
- 1 моль воздуха = 28,96546 г
Наверх
Объемная теплоемкость – обзор
9.4.2 Рабочие жидкости
Чем выше объемная теплоемкость рабочего тела (произведение его плотности на удельную теплоемкость), тем ниже скорость откачки, необходимая для данного потока энтальпии и разности температур, и, следовательно, потери при перекачке будут ниже. Чтобы поддерживать низкие нагрузки на теплообменник, рабочая жидкость не должна требовать чрезмерного давления. Желательно, чтобы рабочая жидкость имела высокую теплопроводность, поскольку это означает, что для достижения заданной скорости теплопередачи необходимы меньшие площади поверхности и разница температур.
Воздух обычно используется в качестве рабочей жидкости, отчасти потому, что он легко доступен, а отчасти потому, что турбомашины уже были разработаны для двигателей с воздушным дыханием. Однако при высоких температурах кислород в воздухе будет окислять определенные материалы, и поэтому может потребоваться инертная рабочая жидкость.
Гелий также можно использовать в качестве рабочего тела. Он инертен и имеет высокую удельную теплоемкость (5,19 кДж / кг К) [45]. Однако он имеет низкую плотность по сравнению с другими рабочими жидкостями и, следовательно, требует повышенного давления для увеличения его объемной теплоемкости (4.2 × 10 3 Дж / м 3 К при 1800 К и 30 бар [45]). Это может привести к высоким напряжениям в теплообменнике. Азот и диоксид углерода также являются потенциальными рабочими жидкостями [6].
Жидкие металлы могут быть привлекательными теплоносителями из-за их высокой объемной теплоемкости. Например, эвтектика свинец-висмут (LBE) имеет объемную теплоемкость порядка 1,4 · 10 6 Дж / м 3 K [46], что больше, чем у гелия. Кроме того, LBE имеет низкую температуру плавления и высокую температуру кипения 397.7K и 1943K, соответственно, при атмосферном давлении [44], что означает, что он существует в виде жидкости во всем интересующем диапазоне сверхвысоких температур без какой-либо необходимости в повышении давления. LBE имеет низкий коэффициент теплового расширения, что облегчает внесение изменений в его объем в диапазоне рабочих температур. Он также обладает хорошей теплопроводностью. Однако его главный недостаток заключается в том, что он вызывает коррозию стали [46]. Олово имеет потенциал для использования в качестве теплоносителя и уже используется в промышленности в расплавленном состоянии для производства стекла [47].Он имеет температуру плавления 232 ° C и точку кипения 2586 ° C [48], что снова означает, что он является жидким во всем интересующем диапазоне сверхвысоких температур. Историческая проблема с использованием жидких металлов заключается в том, что они подвержены риску затвердевания, а затем повреждения любого контейнера при переплавке из-за расширения. Когда жидкий теплоноситель LBE вытек из ядерного реактора советской подводной лодки К-64 в 1972 году, затвердевание сделало весь реактор непоправимым [49].
Удельная теплоемкость воздуха
Удельная теплоемкость воздуха – (Обновлено 26.07.08)Удельная теплоемкость воздуха
Номинальные значения, используемые для воздуха при 300 K: C P = 1.00 кДж / кг. K, C v = 0,718 кДж / кг · K ,, и k = 1,4. Однако все они являются функциями температура, и с чрезвычайно высоким температурным диапазоном опыт работы с двигателями внутреннего сгорания и газотурбинными двигателями получить существенные ошибки. В следующей таблице приведены значения удельная теплоемкость как функция температуры. Мы находим, что выбор значений удельных теплоемкостей в среднем температура каждого процесса дает результаты с разумной точностью (в пределах 1%).
Идеальный газ удельная теплоемкость воздуха
Температура
KC P
кДж / кг.КC v
кДж / кг. Kк
250
1,003
0,716
1.401
300
1,005
0,718
1.400
350
1,008
0,721
1,398
400
1.013
0,726
1,395
450
1.020
0.733
1,391
500
1.029
0,742
1,387
550
1.040
0,753
1,381
600
1.051
0,764
1,376
650
1.063
0,776
1,370
700
1,075
0,788
1,364
750
1.087
0,800
1,359
800
1.099
0,812
1,354
900
1,121
0,834
1,344
1000
1.142
0,855
1,336
1100
1,155
0,868
1,331
1200
1,173
0,886
1,324
1300
1.190
0,903
1,318
1400
1.204
0,917
1,313
1500
1,216
0,929
1,309
Значения до 1000 K были первоначально опубликованы в «Таблицах». термических свойств газов », NBS Circular 564,1955.Последний пять рядов были рассчитаны по формуле BG Kyle “Chemical” и термодинамика процессов “, Englewood Cliffs / Prentice Hall, 1984 и имеют ошибку <1%.
______________________________________________________________________________________
Инженерная термодинамика, Израиль
Уриэли под лицензией Creative
Commons Attribution-Noncommercial-Share Alike 3.0 Соединенные Штаты
Лицензия
Тепловая мощность и накопление энергии
Тепловая мощность и накопление энергии
Когда наша планета поглощает и излучает энергию, изменяется температура, и взаимосвязь между изменением энергии и изменением температуры материала заключена в понятие теплоемкости, иногда называемой удельной теплотой.Проще говоря, теплоемкость выражает, сколько энергии вам нужно, чтобы изменить температуру данной массы. Предположим, у нас есть кусок породы весом один килограмм, и у породы есть теплоемкость 2000 Дж на килограмм на ° C – это означает, что нам нужно добавить 2000 Джоулей энергии, чтобы повысить температуру камня на 1 ° C. Если бы наш камень имел массу 10 кг, нам потребовалось бы 20 000 Джоулей, чтобы получить такое же повышение температуры. Напротив, теплоемкость воды составляет 4184 Джоулей на кг на градус Кельвия, поэтому вам потребуется вдвое больше энергии, чтобы изменить ее температуру на такую же величину, что и у камня.
История охлаждения воздуха и водыЩелкните, чтобы увидеть текстовое описание
История охлаждения двух одинаковых кубов – один из воздуха, другой из воды, при одинаковой начальной температуре (293 ° K, что составляет 20 ° C). В этой модели кубики теряют тепло с поверхности площадью 1 м2 и не получают энергии от своего окружения, что все равно что сказать, что они находятся в вакууме. Если вы сделаете это на заднем дворе, окружающий воздух будет отдавать тепловую энергию кубам, если их температура упадет ниже температуры окружающей среды.Обратите внимание, что сначала температура воздуха падает очень быстро, но с каждым падением температуры он выделяет меньше энергии в течение следующего промежутка времени, поэтому скорость охлаждения снижается. Напротив, вода остывает очень и очень медленно; энергия, которую он излучает, – это капля в ведре (так сказать) по сравнению с общим количеством энергии во всем кубическом метре, поэтому изменение температуры невелико.
Предоставлено: Дэвид Байс © Университет штата Пенсильвания имеет лицензию CC BY-NC-SA 4.0.Теплоемкость материала, а также его общая масса и температура говорят нам, сколько тепловой энергии хранится в материале.Например, если у нас есть квадратная ванна, полная воды в один метр глубиной и один метр по бокам, то у нас есть один кубический метр воды. Так как плотность воды составляет 1000 кг / м 3 , эта ванна имеет массу 1000 кг. Если температура воды составляет 20 ° C (293 ° K), то мы умножаем массу (1000) на теплоемкость (4184) на температуру (293) в ° K и получаем, что в нашем кубическом метре воды 1,22 e9 (1,2 миллиарда) Джоулей энергии. Представьте на мгновение два расположенных рядом кубических метра материала – один кубик воды, а другой воздух.Воздух имеет теплоемкость около 700 джоулей на кг на ° К и плотность всего 1,2 кг / м 3 , поэтому его начальная энергия будет 700 x 1 x 1,2 x 293 = 246120 джоулей – крошечная доля тепловой энергии. энергия, хранящаяся в воде. Если два кубика имеют одинаковую температуру, они будут излучать одинаковое количество энергии со своих поверхностей в соответствии с законом Стефана-Больцмана, описанным выше. Если энергия, потерянная за какой-то промежуток времени, такая же, температура куба воздуха понизится намного больше, чем температура воды, и поэтому в следующий промежуток времени вода будет излучать больше энергии, чем воздух, но воздух охладится еще больше, поэтому будет излучать меньше энергии.В результате температура водяного куба намного стабильнее воздуха – вода меняется намного медленнее; он дольше сохраняет свою температуру. На рисунке выше показаны результаты компьютерной модели, которая отслеживает температуру этих двух кубиков.
Один из способов резюмировать это – сказать, что чем выше теплоемкость, тем больше тепловая инерция, а это означает, что сложнее добиться изменения температуры. Эта концепция важна, поскольку Земля состоит из материалов с очень разной теплоемкостью – воды, воздуха и горных пород; они по-разному реагируют на нагрев и охлаждение.
Теплоемкость некоторых распространенных материалов приведена в таблице ниже.
| Вещество | Теплоемкость (Джкг -1 K -1 ) |
|---|---|
| Вода | 4184 |
| Лед | 2008 |
| Средняя порода | 2000 |
| Мокрый песок (20% воды) | 1500 |
| Снег | 878 |
| Сухой песок | 840 |
| Озелененные земли | 830 |
| Воздух | 700 |
идеальный газ – Как рассчитать удельную теплоемкость газов
Теплоемкость влажного воздуха следует простейшему рецепту, который вы можете придумать: $$ c_s = 1.\ circ C} $$ где 1,005 – это показатель для сухого воздуха, а $ H $ – количество килограммов водяного пара на килограмм воздуха.
При 20 градусах Цельсия давление насыщенного пара для водяного пара составляет 2,3 кПа. Шестьдесят процентов от этого составляет 1380 Па, примерно 0,014 от общего давления. Это парциальное давление не представляет собой процент от массы. Сухой воздух имеет 29 г / моль или около того, вода – 16 + 1 + 1 = 18 г / моль, так что массовое соотношение 18/29 умноженное на 0,014 = 0,0087. Даже если умножить на 1,82, мы получим 0,016 или около того: мы можем повысить 1.005 до 1.02 самое большее. Влажность не сильно влияет на теплоемкость.
Фактическая причина вашего совершенно другого числа 1300 иная и простая: вы перепутали килограммы и кубические метры.
Для уверенности, скрытая теплота здесь не играет роли, потому что никакие фазы не меняются (конденсируются / испаряются) во время нагрева достаточно влажного воздуха. Не играет роли и теплоемкость жидкой воды: на самом деле вода не является жидкой (большими кусками) в этой задаче.\ circ C $. Слово «объемный» означает, что он рассчитывается на единицу объема. Разделите полученное значение на 1,275 килограмма на кубический метр, плотность воздуха, и вы получите 1,02 кДж / кг на градус в соответствии с результатом в двух абзацах выше.
Теплоемкость отдельных газов легко вычислить, если учесть молярную теплоемкость или, что то же самое (с точностью до умножения на постоянную Авогадро), теплоемкость отдельной молекулы. Сферически-симметричный атом будет иметь $ 3k / 2 $, двухатомный – $ 5k / 2 $, более общие молекулы, которые помнят точную ориентацию всего, имеют $ 3k $ и т. Д.Умножьте это на $ N_A $, чтобы получить молярную теплоемкость $ 3R / 2 $ и т. Д. Это также можно разделить на молярную массу, чтобы получить удельную теплоемкость и т. Д. Если вы рассматриваете соответствующее средневзвешенное значение молекул / атомов, которые образуют вверх воздухом, вы также можете рассчитать теплоемкость воздуха. Термодинамика разбавленных газов проста, потому что взаимодействия настолько слабые, что мы действительно суммируем простые свойства только отдельных молекул.
Тепловая масса – Энергетическое образование
Рисунок 1.Схема стены Тромба, эта установка будет использовать тепловую массу на дальней правой стене для удержания тепла. [1]Термическая масса относится к материалу внутри здания, который может помочь уменьшить колебания температуры в течение дня; Таким образом, снижается потребность самого здания в отоплении и охлаждении. Термомассы достигают этого эффекта, поглощая тепло в периоды высокой солнечной инсоляции и выделяя тепло, когда окружающий воздух начинает охлаждаться.При использовании в технологиях пассивного солнечного отопления и охлаждения тепловая масса может сыграть большую роль в сокращении энергопотребления здания.
Свойства термической массы
Идеальный материал для тепловой массы будет иметь:
Теплоемкость вещества – это количество тепловой энергии, необходимое для изменения температуры объекта на заданную величину. Единица СИ для теплоемкости – Джоуль на Кельвин ( Дж / К ). Общее количество энергии, запасенной системой тепловой массы, пропорционально размеру системы или материала, поэтому удельная теплоемкость ( Дж / м 2 K ), теплоемкость на единицу массы и объемная теплоемкость ( Дж / м 3 K ), теплоемкость на единицу объема, являются общими показателями, используемыми для определения материала с хорошей теплоемкостью.
Термомассовые материалы
Ниже приведена таблица стандартных строительных материалов, их теплоемкости, плотности и удельной теплоемкости. Как упоминалось ранее, хороший материал для термической массы должен иметь высокую объемную теплоемкость.
| Материал | Теплоемкость ( Дж / К ) | Плотность ( кг / м 3 ) | Объемная теплоемкость Производительность ( МДж / м 3 K ) |
|---|---|---|---|
| Вода | 4.18 | 1000 | 4,18 |
| Гипс | 1,09 | 1602 | 1,746 |
| Воздух | 1,0035 | 1,204 | 0,0012 |
| Бетон | 0,88 | 2371 | 2,086 |
| Кирпич | 0,84 | 2301 | 2,018 |
| Известняк | 0,84 | 2611 | 2.193 |
| Гранит | 0,79 | 2691 | 2,125 |
| Дерево | 0,42 | 550 | 0,231 |
Вода имеет очень привлекательные термомассовые свойства и может быть привлекательным материалом для пассивных солнечных элементов; однако потенциальные проблемы с утечкой воды и повреждениями не позволяют его широко использовать в качестве носителя для хранения тепла. Бетон и кирпич обладают относительно высокой объемной теплоемкостью и являются обычными строительными материалами.При правильном использовании с солнечной стеной или стеной с тромбом потребление энергии для отопления и охлаждения здания может быть значительно снижено.
Материалы фазового перехода
В традиционных материалах с термальной массой используется физическое тепло для хранения и выделения пассивной энергии солнечного излучения. В материалах с фазовым переходом используется скрытый накопитель тепла, и они могут поглощать такое же количество солнечной энергии, используя гораздо меньший объем материала. [3] При повышении температуры материал меняет фазы с твердой на жидкую, это эндотермическая реакция, поэтому он поглощает тепло.Когда окружающая среда остывает (ночью), материал превращается из жидкого в твердое, в результате экзотермической реакции выделяется накопленное тепло в здание. Использование материалов с фазовым переходом – относительно новая концепция в строительной науке, существует множество различных материалов, используемых для самых разных приложений.
Тепловая масса и климат
В теплую погоду тепловая масса может поглощать тепло, полученное от солнечного света. Это сделает внутреннее пространство более комфортным и значительно снизит потребность в охлаждении и стоимость кондиционирования воздуха.Ночью, когда здание охлаждается, накопленная тепловая энергия затем выделяется во внутреннее пространство здания, что снижает потребность в тепле. Тепловая масса наиболее выгодна в климате, где есть большие колебания между дневной и ночной температурой окружающей среды. В областях с высокими ночными температурами все еще можно использовать тепловую массу, тогда здание необходимо проветривать ночью более прохладным ночным воздухом для отвода накопленной тепловой энергии. [4]
Список литературы
- ↑ Wikimedia Commons.(6 августа 2015 г.). Стена для тромба [Онлайн]. Доступно: https://upload.wikimedia.org/wikipedia/commons/3/3d/Illust_passive_solar_d2_319pxW.gif
- ↑ Построй Зеленую Канаду. (28 августа 2015 г.). Объяснение тепловой массы [Online]. Доступно: http://www.buildgreen.ca/2008/09/an-explanation-of-thermal-mass/
- ↑ Ф. Кузник, Д. Давид, К. Йоханнес и Ж.-Ж. Ру, «Обзор материалов с фазовым переходом, интегрированных в стены зданий», Renew. Поддерживать. Энергия Rev., т. 15, нет. 1. С. 379–391, январь 2011 г.
- ↑ Г. П. Хенце, Т. Х. Ле, А. Р. Флорита и К. Фельсманн, «Анализ чувствительности оптимального контроля тепловой массы здания», J. Sol. Energy Eng., Т. 129, нет. 4, стр. 473, 2007. 129, вып. 4, стр. 473, 2007.
Теплоемкость воздуха.
Разговоры о нагревании океанов и таянии полярных льдов из-за углекислого газа ненаучны по той простой причине, что в воздухе недостаточно теплоемкости для этого.
Теплоемкость (называемая удельной теплотой) воздуха составляет 1,0035 джоулей на грамм на градус Цельсия (Дж / г / C), что равно килоджоулей на килограмм на градус Цельсия (кДж / кг / C).
Удельная теплоемкость воды составляет 4,1813 Дж / г / C или 1 калорию / г / C.
Плотность воздуха при температуре 15 ° C и уровне моря составляет 1,225 килограмма на кубический метр.
Плотность воды 1000 кг / м3. Морская вода немного плотнее, но мы не будем это учитывать.
Следовательно, кубический метр воды содержит в 3401 раз больше тепла, чем кубический метр воздуха при той же температуре. (4,18131,0035×1,0001,225 = 3401)
Это означает, что для нагрева кубического метра воды на 0,2 ° C из воздуха потребуется 3401 кубический метр воздуха с потерей 0,2 ° C. Если бы океаны были нагреты на 0,2 ° C до глубины 350 метров (половина глубины измерений ARGO), должно было бы быть 167 атмосфер и воздуха, теряющего 0,2 ° C. (350×34015кмx70% = 167) (Высота нормальной атмосферы 12-15 км.Приблизительное среднее значение – это предположить, что все это давление на уровне моря на высоте 5 км. Океаны покрывают 70% поверхности Земли.) Это означает, что 167 раз больше планеты Земля , чтобы поедать океаны, как утверждается.
Воздуха не так много, но фейки утверждают, что океаны нагрелись на 0,2 градуса из-за глобального потепления. Это полная выдумка. В воздухе нет достаточного количества тепла, чтобы хоть сколько-нибудь нагреть океаны.
В условиях повышения температуры в Мировом океане
Если атмосфера отказала 0.2C к океанам, количество тепла, которое он может передать океанам, теоретически вызовет повышение температуры примерно на 0,001C на для одной десятой верхней части океанов.
Расчеты таковы: Воздух имеет теплоемкость 1 кДж / кг / C. Плотность воздуха 1,23 кг / м3. Атмосфера имеет высоту, эквивалентную 5 км при давлении на уровне моря. Столбец в один квадратный метр имеет 6 150 кДж / Кл (1×1,23×5 000 = 6 150). При переносе 0,2C остается доступным 1230 кДж (6 150×0,2 = 1230).Вода имеет теплоемкость 4,18 кДж / кг / C. Плотность 1000 кг / м3. Колонна до глубины 350 м имеет пропускную способность 1,46×10 6 кДж / C (4,18×1,000×350 = 1,46×10 6 ). Разделив его на имеющиеся 1230 кДж, мы получим повышение температуры в океане на 0,001 ° C.
Тающий лед
Таяние полярных льдов с воздухом еще более смешно, потому что таяние льда требует много тепла, называемого теплотой плавления, которое составляет 334 кДж / кг. На каждый кубический метр растаявшего льда потребуется 261000 м воздуха , теряя 1С (3340001.28 = 261 000). (Кубический метр воды или льда составляет около 1000 кг. Для плавления требуется 334 кДж / кг. В совокупности это 334000 кДж / м. Удельная теплоемкость воздуха составляет 1 кДж / кг при плотности 1,28 кг / м при 0 ° C.)
Это число можно разделить на высоту атмосферы, которая эквивалентна 5 км при нормальном давлении, и это 52 атмосферы над льдом. (261 0005 000 = 52). Это для одного метра толщины льда и 1С глобального потепления. Если толщина льда составляет 10 метров, потребуется 520 атмосфер выше, чтобы удерживать достаточно тепла, чтобы растопить его.
Конечно, воздух недостаточно хорошо циркулирует на высоте более нескольких километров. На самом деле происходит то, что воздух над полярным льдом быстро становится той же температуры, что и лед, и ничего не тает. Чтобы растопить полярный лед, нужны теплые океанские течения. Таяние, происходящее на Северном полюсе, является результатом протекания теплой воды Тихого океана через Берингов пролив в район Северного полюса.
Лед на Южном полюсе становится все толще, потому что он находится над сушей.Потепление океанических течений увеличивает влажность воздуха, в результате чего над Антарктидой появляется снег. По краям небольшое количество льда тает из-за потепления океанских течений. Почему океанские течения теплые и прохладные, никто не знает, за исключением того, что температура океана медленно повышается между ледниковыми периодами, а океаны чрезвычайно неоднородны по температуре.
Ледники в горах не имеют никакого значения, потому что обычно они слишком малы. Только Гималаи большие, и они не тают, потому что они слишком высоки, чтобы до них могли добраться потоки теплого воздуха.Лед низкого уровня растаял вскоре после последнего ледникового периода. Края горных ледников постоянно увеличиваются и уменьшаются по случайным причинам. Этот эффект продемонстрировал «ледяной человек», найденный в Альпах после таяния льда. Он умер там около 5000 лет назад. Это означает, что там, где он находился около 5000 лет назад, льда не было, затем его покрыл лед, а затем лед снова растаял несколько лет назад. Такое таяние и преобразование льда не имеет ничего общего с парниковыми газами.
Откуда поступает тепло?
Последнее утверждение состоит в том, что 90% тепла, производимого парниковыми газами, уходит в океаны.Это утверждение – одна из попыток объяснить, почему не было обнаружено никаких изменений средней приповерхностной температуры за последние 18 лет.
Обо всем этом уже позаботились климатологи, и это не тот результат, который у них получился. До недавнего времени они не учитывали ни капли тепла, поступающего в океаны. Фактически, когда были сделаны первые измерения ARGO, около десяти лет назад, в результате океаны слегка остыли. Так что самые холодные измерения были выброшены, а температура была стабильной.
Затем, в 2015 году, был сделан противоречивый расчет, показавший, что океаны нагрелись на 0,2 ° C из-за глобального потепления, и поэтому температура воздуха не повышается, как ожидалось. Как объяснялось выше, это больше тепла, чем могут учесть парниковые газы. Последние 40 лет климатологии якобы объяснили все тепло, и ни одно из них не пошло на нагревание океанов. Разве последние 40 лет расчетов и измерений не должны быть завершены? Об этом никто не говорит ни слова.Противоречия такого рода существуют в каждом пункте климатологии, потому что этот предмет полностью надуманный и не имеет отношения ни к чему, что происходит в природе. Противоречия скорее игнорируются, чем разрешаются.
Обфусцированная методология заключалась в следующем: тепло, выделяемое углекислым газом (первичный эффект), было рассчитано с использованием «уравнений переноса излучения», показывающих, что 3,7 Вт / м энергии, меньшей, чем энергия Солнца, задерживается в атмосфере и не выходит в космос. при удвоении количества СО2 в воздухе.Эти 3,7 Вт / м преобразуются в повышение температуры у поверхности на 1 ° C путем применения постоянной Стефана-Больцмана в обратном порядке.
Поскольку атмосфера приближается к удвоению содержания CO2, предполагаемые измерения приближаются к показанию ожидаемого повышения температуры на 1 ° C, демонстрируя божественную точность и мудрость климатологии. Ничто из этого не объясняет попадание тепла в океаны.
Что касается вторичных эффектов, то были рассчитаны и смоделированы некоторые данные об океанах, но никаких объяснений опубликовано не было.Если первичный эффект не нагревает океаны, то почему вторичный эффект? Модели показали непрерывный рост, которого не происходило за последние 18 лет; а затем в качестве объяснения было использовано тепло океана. Поскольку модели показали увеличение, а не произошло, модели не должны были учитывать тепло океана.
Почему ожидаемое повышение температуры на 1С было обнаружено с такой точностью, если 90% тепла уходило в океаны и не учитывалось при анализе первичных или вторичных эффектов? Ответ прост: без противоречий выдумывать ложь невозможно.