А.А. Мальшин Определение удельной теплоемкости воздуха при постоянном давлении
МИНИСТЕРСТВООБРАЗОВАНИЯРОССИЙСКОЙФЕДЕРАЦИИ ГОСУДАРСТВЕННОЕУЧРЕЖДЕНИЕ
КУЗБАССКИЙГОСУДАРСТВЕННЫЙТЕХНИЧЕСКИЙУНИВЕРСИТЕТ КАФЕДРА ФИЗИКИ
ОПРЕДЕЛЕНИЕ УДЕЛЬНОЙ ТЕПЛОЕМКОСТИ ВОЗДУХА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
Методические указания к лабораторной работе № 303 по курсу общей физики для подготовки студентов по всем направлениям
Составители А. А. Мальшин В. П. Корчуганов
Утверждены на заседании кафедры Протокол №1 от 30.08.01 Рекомендованы к печати методической комиссией направления 550600 Протокол №3 от 2.10.01 Электронная копия находится в
библиотеке главного корпуса ГУ КузГТУ
Кемерово 2002
1
ОПРЕДЕЛЕНИЕ УДЕЛЬНОЙ ТЕПЛОЕМКОСТИ ВОЗДУХА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
Данная лабораторная работа относится к разделу «Молекулярная физика и термодинамика», тема «Законы термодинамики».
Перед занятием студент обязан самостоятельно подготовиться к лабораторной работе (см.
п. 3). На выполнение и защиту данной работы отводится 2 часа аудиторных занятий.
1.ЦЕЛИ РАБОТЫ:
1)освоить принципы определения удельной теплоемкости при постоянном давлении методом протока;
2)определить удельную теплоемкость воздуха при постоянном давлении;
3)изучить методы измерения разности температур и расхода воздуха.
2.ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ:
установка для определения удельной теплоемкости при постоянном давлении.
3.ПОДГОТОВКА К РАБОТЕ:
1)изучить теоретические положения, касающиеся данного явления по литературным источникам [1-3];
2)изучить данные методические указания;
3)ответить на контрольные вопросы на с. 10.
4.ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Передача энергии от одного тела к другому может быть осуществлена двумя способами: первый способ – посредством механического взаимодействия, когда совершается работа; второй способ – посредством теплового взаимодействия, когда энергия передается хаотическим движением молекул за счет теплопроводности или теплового излучения.
Первое начало термодинамики говорит о том, что теплота, сооб-
щаемая телу, расходуется на изменение внутренней энергии системы и на совершение телом работы против внешних сил:
∂Q = d U +∂A. | (1) |
2
Одним из основных тепловых свойств тел, широко используемых в термодинамическом методе исследования, является теплоемкость.
Теплоемкостью тела называется физическая величина, численно равная отношению теплоты, сообщаемой телу, к изменению температуры тела Т в рассматриваемом термодинамическом процессе:
С = | ∂Q | . | (2) |
| d T |
| |
Теплоемкость тела зависит от его химического состава, массы тела и его термодинамического состояния, а также от вида процесса изменения состояния тела, в котором поступает теплота ∂Q.
Тепловые свойства однородных тел характеризуются понятиями удельной Сm и молярной теплоемкости CM
Удельной теплоемкостью называется физическая величина, равная теплоте, необходимой для нагревания одного килограмма вещества на один кельвин:
Cm = m∂dQT ,
где m – масса тела.
Молярной теплоемкостью называется ная теплоте, необходимой для нагревания один кельвин:
СM = M ∂Q m d T
физическая величина, раводного моля вещества на
,
где М – молярная масса вещества. Связь между теплоемкостями:
C = m Cm = | m | CM . | (3) |
| |||
| M |
| |
Тогда можно записать количество теплоты в виде:
∂Q = C d T = m Cm d T = Mm CM d T .
Так как ∂Q по формуле (1) определяется изменением внутренней энергии dU и работой расширения ∂A, то теплоемкость также зависит от изменения объема.
Для твердых тел и жидкостей изменение объема при нагревании относительно невелико, поэтому для них зависимостью теплоемкости от изменения объема обычно пренебрегают. Для газов, объем которых сильно меняется с температурой, пренебрегать зависи-
3
мостью ∂Q и теплоемкости от изменения объема нельзя.
Применим уравнение (1) к различным изопроцессам идеальных газов:
а) при изохорном процессе (V = const) газ не совершает работу. По первому началу термодинамики вся теплота, сообщаемая газу в изохорном процессе, идет на изменение его внутренней энергии.
∂Q = d U = | m | CMv d T , | ∂A = 0, | (4) |
| ||||
| M |
|
| |
где CMV – молярная теплоемкость газа при постоянном объеме;
б) при изобарном процессе (p = соnst) уравнение первого начала термодинамики можно записать в виде:
m | CMp d T = | m | CMv d T + p d V, | (5) |
M |
| |||
| M |
| ||
где СMP – молярная теплоемкость газа при постоянном давлении.
Выразим элементарную работу из уравнения Менделеева – Кла-
пейрона:
∂A = p d V = | m | R d T . | (6) |
| |||
| M |
| |
Для установления связи между молярными теплоемкостями СМP и СMV подставим (6) в (5). Получаем:
СM P −CM V = R .
Это соотношение называется уравнением Майера. Для удельных теплоемкостей Сmp и Cmv оно имеет вид:
Cmp −Cmv = MR .
Физический смысл уравнения Майера заключается в том, что при изобарном нагревании газа к нему должна быть подведена большая теплота, чем для изохорного нагревания в одном и том же диапазоне температур;
в) при изотермическом процессе (T = const) внутренняя энергия идеального газа не изменяется и вся теплота, сообщаемая газу, расходуется на совершение газом работы против внешних сил (V2 > V1 – расширение).
∂Q = ∂A , или | Q | = A | = | m | RT ln | V2 | , d U = 0, | (7) |
|
| |||||||
| 12 | 12 |
| M |
| V1 |
|
|
|
|
|
|
|
|
|
так как dT = 0, следовательно, теплоемкость равна бесконечности;
4
г) для адиабатного процесса ∂Q = 0 и С = Cm = CM = 0.
Теория теплоемкостей газов, которую называют классической, в отличие от квантовой, была разработана Больцманом и Максвеллом.
Эта теория основывается на законе о равномерном распределении энер-
гии по степеням свободы молекул. Молекула одноатомного газа имеет три степени свободы поступательного движения относительно трех координатных осей. На каждую степень свободы приходится энергия:
Ei = 12 k T.
В общем случае для моля многоатомного идеального газа:
EM = NA Ei = 2i NA k T = 2i R T ,
отсюда мольная теплоемкость для идеального газа:
CMV = | i | R , | СMP = CMV + R = ( | i | +1) R . |
|
| ||||
2 |
| 2 |
| ||
Определение теплоемкости тел обычно производится в калориметрах, т.е. в сосудах, обеспечивающих теплоизоляцию исследуемого тела от внешней среды. При этом регистрируется теплота ∆Q, получаемая телом, и изменение температуры тела ∆T.
Теплоемкость тела находится как частное от деления ∆Q на ∆Т:
С = ∆∆QT .
Надежность измерения определяется в основном, качеством калориметра. Необходимо, чтобы количество теплоты, затрачиваемое на нагревание исследуемого тела, было существенно больше теплоты, расходуемой на нагревание калориметра и на потери, связанные с утечкой теплоты из установки. При измерении теплоемкости воздуха эти требования выполнить очень трудно, так как масса воздуха, заключенного в калориметре, и, следовательно, количество теплоты, идущей на его нагревание, очень малы.
Чтобы увеличить количество воздуха при неизменных размерах установки, в данной работе воздух продувается сквозь калориметр, внутри которого установлен нагреватель. Определяются количество теплоты ∂Q, отдаваемое нагревателем, масса m протекающего воздуха и изменение его температуры ∆Т. Удельная теплоемкость воздуха при постоянном давлении находится по определению:
| 5 |
| |
Сmp = |
| ∆Q | (8) |
| m ∆T | ||
|
|
| |
5.
УСТРОЙСТВО, ПРИНЦИП РАБОТЫ УСТАНОВКИ И МЕТОДИКА ИЗМЕРЕНИЙ
Принципиальная схема установки показана на рис.1. Воздух прокачивается компрессором через трубку 1, размещенную в теплоизолирующей оболочке 2.
Измерение расхода воздуха производится по перепаду давлений на капилляре, который вместе с трубой образует единую проточную магистраль. Протекая через трубку, воздух нагревается электрической спиралью 3. Разность температур на входе и выходе трубки измеряется дифференциальной термопарой 4. ЭДС термопары измеряется вольтметром, подключаемым к ней через разъем 5. Электрический нагреватель
3 питается постоянным током от | Рис. 1. Схема установки |
блока питания УБП, подключенно- |
го к нагревателю через соответствующие разъемы. Напряжение на нагревателе измеряется вольтметром, подключаемым через разъемы 7. Ток в нагревателе определяется по измеренному вольтметром, подключаемым к разъемам 6, напряжению UR на образцовом сопротивлении
Rобр = 0,1 Ом:
Iн = | UR |
| (9) | |
Rобр. | ||||
|
| |||
Определяем количество теплоты, отдаваемое нагревателем возду- | ||||
ху за время t, по закону Джоуля-Ленца: |
| |||
∆Q = Iн Uн t | (10) | |||
Массовый расход воздуха z через трубку, определяемый как масса воздуха, протекающего через поперечное сечение трубки в единицу времени
|
|
|
| 6 |
|
|
|
|
|
|
|
|
| z = | m |
|
|
| (11) | ||
находим по формуле Пуазейля: | t |
|
| |||||||
|
|
|
|
|
| |||||
π r4 |
|
|
|
|
|
| ||||
|
|
| ρ ∆P t |
|
|
| ||||
|
| η = |
| 0 |
|
|
| , |
| |
| m |
| 8 l V |
| ||||||
|
|
|
|
|
| |||||
где объем V = | , откуда |
|
|
|
|
|
|
|
| |
ρ |
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| |
|
|
|
| π r4 ρ ∆p |
| |||||
|
| z = |
| 0 |
|
|
| (12) | ||
|
|
| 8 l η |
|
| |||||
|
|
|
|
|
|
|
| |||
где радиус капилляра – r0 = 4,5 10 −4 м, длина капилляра – l = 6 10 −2 м , коэффициент внутреннего трения воздуха при данной температуре –
η = 1,8 10-5 мкгс, перепад давлений на концах капилляра – ∆р = ρжgh, где
плотность воды ρж =103 кг/м3, перепад уровней жидкости в манометре – h , плотность воздуха – ρ = 1,29 кг/м3.
Перепад температур на концах трубки определяем по измеренной термо ЭДС ε из формулы
∆T = | ε | , | (13) | |
α | ||||
|
|
|
где коэффициент α = 0,00671 В/град для данной термопары. Подставляя (9), (10), (11), (12), (13) в уравнение (8), получаем ра-
бочую формулу
Cmp = B | Uн U |
| |
R | , | (14) | |
| |||
| h ε |
| |
где B – постоянная для данной установки:
B = | 8 l α η | = 0,356 | Дж м | . |
π g Rобр ρж ρ r04 |
| |||
|
| кг К В | ||
7
6.ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
6.1.Присоединить гибкий шланг к воздушным штуцерам на обоих модулях (см. рис. 2).
6.2.Соединить проводами клеммы источника питания на измерительном модуле и клеммы «Ист. пит.» на модуле стенда.
6.3.Соединить проводами клеммы «Вольтм.» модуля стенда и
клеммы « » и «U» мультиметра измерительного стенда.
6.4.Вывести регулятор напряжения источника питания на измерительном стенде в крайнее положение, вращая ручку против часовой стрелки. На переключателе пределов мультиметра (левый вертикальный ряд кнопок) установить предел напряжения 20В, для этого нажать кнопку «20В». Все остальные кнопки переключателя пределов должны быть отжаты.
6.5.На измерительном стенде включить тумблеры «Сеть», «Источник питания», «Компрессор», а также движок выключателя мультиметра (он находится справа вверху на панели мультиметра).
6.6.Нажмите клапан «Напуск» на модуле стенда и добейтесь, чтобы разность уровней жидкости h в U-образном манометре составила
50-100 мм.
6.7.Нажать кнопку RА на модуле стенда и с индикатора мультиметра произвести отсчёт напряжения UН на нагревателе, при этом величина этого напряжения устанавливается поворотом ручки регулятора напряжения источника питания по часовой стрелке.
6.8.Нажать кнопку RБ на модуле стенда и с индикатора мультиметра произвести отсчёт напряжения UR на образцовом сопротивлении, для этого переключить предел измерения мультиметра на 200 мВ (нажать кнопку «200mV» на переключателе пределов мультиметра).
6.9.Нажать кнопку на модуле стенда и снять отсчет напряжения на термопаре по индикатору мультиметра в момент, когда показания мультиметра перестанут изменяться (примерно через 5 минут при постоянной разности уровней h), после чего перейти на предел измерения
«20 V».
6.10.Пункты 6.7 – 6.9 повторить для следующих четырёх значений напряжения UН на нагревателе (6 В, 8 В, 10 В, 12 В).
Результаты
измерений занести в таблицу. Рассчитать Cmp по формуле (14).
8
Рис.2. Блок-схема установки.
Слева показан измерительный модуль, справа – модуль стенда
9
6.11. Рассчитать удельную теплоемкость для воздуха по формуле
i |
| R |
| ||
Cmp= |
| + 2 |
| , взять i = 5, M = 0,029 кг/моль. Сравнить полученное | |
2 | M | ||||
|
|
| |||
значение со средней удельной теплоемкостью при постоянном давлении, определенное по данным лабораторной работы.
Измеряемые параметры и рассчитанная удельная теплоемкость при постоянном давлении
№ | Uн | h | ε | UR |
| Cmp | |
опыта | B | м | В | В |
| Дж |
|
| кг К | ||||||
|
|
|
|
|
| ||
1 | 2 |
|
|
|
|
|
|
2 | 4 |
|
|
|
|
|
|
3 | 6 |
|
|
|
|
|
|
4 | 8 |
|
|
|
|
|
|
5 | 10 |
|
|
|
|
|
|
7.
ИССЛЕДОВАТЕЛЬСКОЕ ЗАДАНИЕ
Оценить величину тепловых потерь, считая, что потери тепла зависят только от распределения температур вдоль стенок, а значит, перепада температур на спаях термопары, и не зависят от мощности нагревателя и потока воздуха. Это позволяет экспериментальным путем найти и исключить потери тепла в калориметре. Тогда:
Сmp= | ∆Q | = | IH VH − N | , | |
m ∆T | m ∆T | ||||
|
|
|
где IHVH – мощность, выделяемая нагревателем; N – мощность тепловых потерь; m – масса воздуха, проходящего через калориметр за единицу времени; ∆Q – теплота; ∆Т – разность температур.
1. По полученным результатам для всех измерений постройте графики, откладывая по оси абсцисс мощность нагревателя IHVH , а по оси ординат – величину m∆T; угол наклона прямой, проведенной через точки графика, определяет искомую теплоемкость воздуха при посто-
лабораторная работа 209
Лабораторная работа № 209
ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ ВОЗДУХА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ И ПОСТОЯННОМ ОБЪЕМЕ
Цель работы: определить методом Клемана-Дезорма отношение теплоемкостей воздуха
при постоянном давлении и постоянном объеме.
Приборы и принадлежности:
стеклянный баллон,
насос Камовского,
U–образный водяной манометр,
соединительные шланги.
1. ТЕПЛОЕМКОСТЬ ИДЕАЛЬНОГО ГАЗА
В молекулярной физике термодинамическое состояние газа характеризуется параметрами состояния: давлением Р, объемом V, температурой Т, массой m и т.д. Уравнение, связывающие эти величины называется уравнением состояния вещества. Для случая идеального газа уравнением состояния является уравнение Менделеева-Клапейрона, которое имеет вид:
(1)
где R – молярная газовая постоянная, m – масса одного моля газа.
Теплоемкостью вещества называется величина, равная количеству теплоты,
которое нужно сообщить веществу, чтобы изменить его температуру на один
градус.
Математически это определение записывается следующим образом:
где dQ – бесконечно малое количество теплоты, при сообщении которого изменяется температура вещества на dT. Теплоемкость вещества измеряется в Дж/K.
На практике часто пользуются понятиями удельной и молярной теплоемкостей вещества. Удельная теплоемкость – теплоемкость единицы массы вещества, т.е. она равна количеству теплоты, которое нужно сообщить единице массы вещества, чтобы изменить его температуру на один градус:
Молярная теплоемкость – теплоемкость одного моля вещества, т.е. она равна количеству теплоты, которое нужно сообщить одному молю вещества, чтобы изменить его температуру на один градус:
где – количество молей
вещества (понятие
идеального газа и моля вещества см.
в лаб. раб. № 201).
Удельная и молярная теплоемкости связаны соотношением
Величина теплоемкости газа зависит от условий, при которых он нагревается. Выясним эту зависимость, воспользовавшись уравнением состояния (1) и первым законом термодинамики, который можно сформулировать следующим образом: количество теплоты dQ, сообщаемое термодинамической системе (в нашем случае воздуху), расходуется на увеличение внутренней энергии dU и на совершение системой работы dA против внешних сил. Математическая запись первого закона термодинамики:
(2)
где dU – бесконечно
малое изменение внутренней энергии системы; dQ, dA – соответственно,
бесконечно малая теплота, подводимая к системе и элементарная работа.
Тогда теплоемкость вещества равна
(3)
Из уравнения (3) видно, что теплоемкость имеет различные значения в зависимости от способа нагревания газа, т.к. одному и тому же значению dT могут соответствовать различные значения dU и dA. Элементарная работа в газовом процессе равна
(4)
Рассмотрим основные процессы, протекающие в идеальном газе при изменении температуры, когда количество вещества остается неизменным.
Если нагревание производится при постоянном объеме, то газ не совершает работы над внешними телами и, следовательно, вся теплота идет на приращение внутренней энергии газа:
при .
Тогда молярная теплоемкость газа при постоянном объеме равна:
(5)
Если нагревание происходит при постоянном давлении, то теплота, сообщаемая газу, идет и на изменение внутренней энергии газа и на совершение газом работы против внешних сил:
при
В этом случае молярная теплоемкость газа при постоянном давлении равна:
(6)
Дифференцируя уравнение (1), получим:
(7)
но если Р = const, тогда
(8)
С учетом (8), (4) и (5) уравнение (6) запишется:
(9)
Из формулы (9) следует, что СР > CV на величину R, которая равна работе,
совершаемой молем идеального газа при повышении его температуры на один
градус при постоянном давлении.
Необходимо отметить, что соотношение (9) справедливо только для идеального газа. Отношение теплоемкостей
(10)
представляет собой характерную для каждого газа величину, которая называется постоянной адиабаты.
2. УРАВНЕНИЕ АДИАБАТЫ ИДЕАЛЬНОГО ГАЗА
Процесс, протекающий в термодинамической системе без теплообмена с внешней средой, называется адиабатическим. Первый закон термодинамики для идеального газа в этом случае будет иметь вид:
т.к. dQ = 0 или, используя (2) и (5), запишем
(11)
Разделив уравнение (7) на (11) и учитывая формулу (9), получим:
или
(12)
где Интегрируя и потенцируя формулу (12), получим уравнение адиабаты идеального газа в переменных Р и V:
(13)
Полученное выражение есть
уравнение газового состояния при адиабатическом процессе, называемое также уравнением Пуассона.
3. ВНУТРЕННЯЯ ЭНЕРГИЯ И ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ
МОЛЕКУЛ ИДЕАЛЬНОГО ГАЗА
Из молекулярно-кинетической теории идеального газа следует, что средняя кинетическая энергия молекулы равна
где k – постоянная Больцмана, Т – термодинамическая температура, i – число степеней свободы молекулы газа.
Числом степеней свободы i называют наименьшее
число независимых координат, с помощью которых можно однозначно определить
положение тела в пространстве. Силы, ограничивающие движение тела, называются связями. Если тело движется без
связей, то такое движение тела называется свободным.
Так, свободное положение в пространстве материальной точки полностью
определяется заданием значений трех ее координат (например, х, y, z – в декартовой системе
координат).
В соответствии с этим материальная точка имеет три степени
свободы (i = 3). Если эта точка
движется по некоторой поверхности, то она обладает двумя степенями свободы.
Абсолютно твердое тело
имеет шесть степеней свободы (i = 6). Для определения его
положения в пространстве нужно задать три координаты его центра масс (х,y,z), два угла (например, q и
j), указывающих
направление какой-либо оси, проходящей через центр масс тела и, наконец, угол
y, определяющий направление
второй, связанной с телом оси, перпендикулярной к первой. Степени свободы х, y, z называются поступательными. Изменение любого из
углов q, j, y при неизменном положении центра масс
обуславливается вращением тела, в связи с чем, соответствующие степени
свободы называются вращательными.
Следовательно, из шести степеней свободы абсолютно твердого тела три являются
поступательными и три – вращательными.
Молекулу одноатомного газа можно рассматривать как материальную точку, поэтому число степеней свободы одноатомной молекулы равно трем. Молекулы, состоящие из двух, трех и большего числа атомов не могут быть уподоблены материальным точкам. «Жесткая» молекула двухатомного газа в первом приближении представляет собой два жестко связанных атома, находящихся на некотором расстоянии друг от друга (см. рис. 1а).
Такая молекула напоминает
гимнастическую гантель с невесомой ручкой, обладающую тремя степенями свободы
поступательного движения относительно осей х, y, z,
и двумя степенями свободы вращательного движения вокруг осей х и z. Вращение вокруг третьей
оси y рассматривать не нужно,
т.к. момент инерции атомов относительно этой оси ничтожно мал, а,
следовательно, ничтожно мала и кинетическая энергия молекулы, связанная с
этим вращением.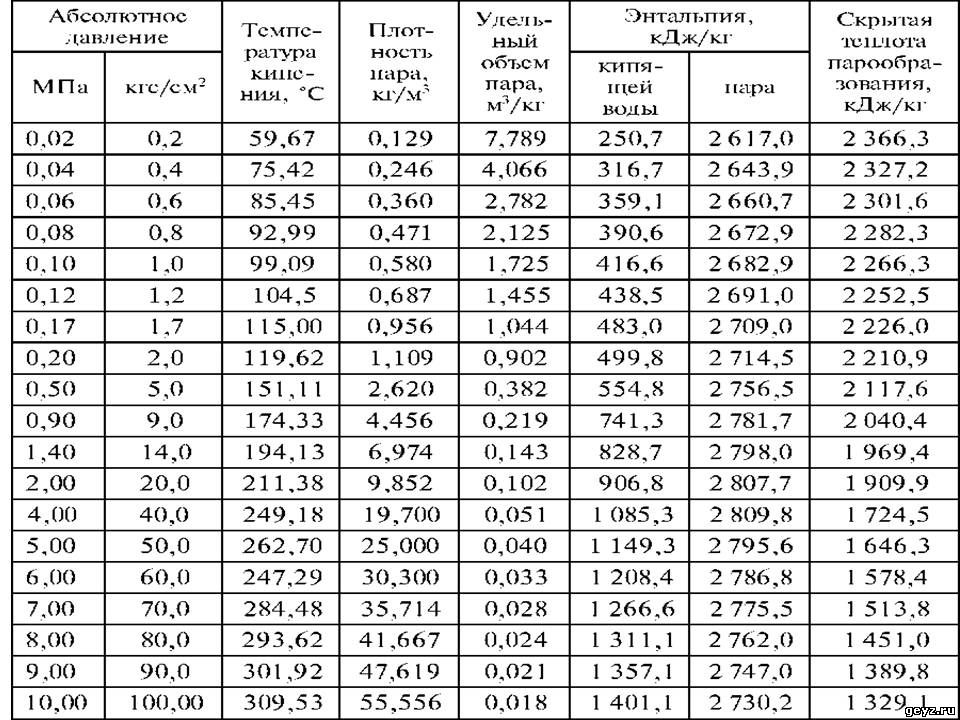
Трехатомные и более сложные молекулы подобно абсолютно твердому телу обладают тремя степенями свободы поступательного движения и тремя степенями свободы вращательного движения (рис. 1b).
Если атомы в молекуле совершают еще и колебания, то кроме кинетической энергии необходимо учитывать потенциальную энергию взаимодействия этих атомов, и как показывает опыт, средняя потенциальная энергия атомов равна их средней кинетической энергии. Тогда полную энергию, приходящуюся на одну колебательную степень свободы, можно считать равной удвоенной ее кинетической энергии. Поэтому при учете колебательных степеней свободы необходимо энергию молекулы увеличивать на величину kT, а число i соответственно на два. В случае молекулы, состоящей из N-атомов, число степеней свободы равно
При этом iпост = 3.
Для линейной молекулы iвращ = 2, iкол = 3N –
5. Для всех других молекул iвращ = 3, iкол = 3N –
6.
Так как молекулы идеального газа не взаимодействуют между собой, то внутреннюю энергию идеального газа массы m можно найти, умножив среднюю кинетическую энергию одной молекулы на число молекул:
т.к. где NA – число Авогадро, а R = kNA.
Сравнение этого выражения с формулой (5) дает, что молярная теплоемкость идеального газа при постоянном объеме равна:
Приняв во внимание формулу (9), найдем молярную теплоемкость идеального газа при постоянном давлении:
Т.
о., постоянная адиабаты для идеального газа
выражается формулой:
(14)
Соотношение (14) позволяет по значению g оценить число степеней свободы молекул газа.
4. ОПИСАНИЕ РАБОЧЕЙ УСТАНОВКИ И
МЕТОДА ИЗМЕРЕНИЙ
Величину g, т.е. отношение теплоемкости
СP газа при постоянном
давлении к его теплоемкости СV при постоянном объеме
можно определить с помощью прибора Клемана-Дезорма, состоящего из стеклянного
баллона 1; крана 2, позволяющего изолировать или
сообщать баллон с атмосферой; крана 3, разобщающего баллон и насос;
насоса 4, служащего для создания в баллоне избыточного давления; U-образного водяного
манометра 5, служащего для регистрации разности между давлением воздуха
в баллоне и атмосферным давлением.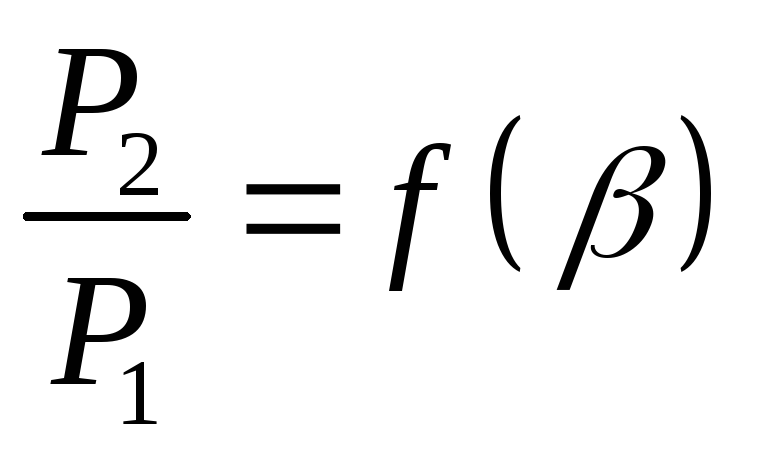
Рис. 2.
В роли крана 2 используется пробка, перекрывающая отверстие в крышке баллона.
Закрывают плотно пробку 2 и открывают кран 3. Небольшими порциями с помощью насоса 4 накачивают воздух в баллон до некоторого давления. Затем с помощью крана 3 разобщают баллон с насосом. Если повышение давления было произведено достаточно быстро, манометрический столбик жидкости не сразу займет окончательное положение, т.к. сжатие воздуха было близким к адиабатическому, и, следовательно, температура его повысилась. Окончательная разность уровней в манометре (h) установится только тогда, когда температура воздуха внутри сосуда сравняется благодаря теплопроводности стенок с температурой окружающего воздуха.
Обозначим через Т1 абсолютную температуру окружающего воздуха и через Р1 – давление газа внутри сосуда, тогда после накачки воздуха
(15)
где – избыточное
давление воздуха в баллоне над внешним – атмосферным Р0, обусловленное накачкой
воздуха.
Пусть параметры Т1, V1 и Р1 характеризуют состояние газа, которое будем называть первым состоянием (состояние 1, см. рис. 3). Здесь V1 – объем той массы m воздуха, которая при любых протекающих в баллоне процессах остается постоянной.
Газовые законы обычно применяются для расчетов изменений, происходящих с газом, масса которого остается постоянной. В нашем же случае часть воздуха выходит из баллона при сообщении его с атмосферой. Поэтому все дальнейшие рассуждения относятся не ко всему воздуху в баллоне, а лишь к той его части, которая все время присутствует в баллоне и остается в нем после его разобщения с атмосферой в точке 3 (рис. 3). Остальная часть воздуха может рассматриваться как поршень, который выдвигается из баллона при расширении.
Если теперь быстро
открыть пробку 2, то воздух в сосуде будет расширяться адиабатически, пока
давление его не сделается равным атмосферному Р0; при этом он охладится до температуры Т2.
Это будет второе
состояние газа (состояние 2).
Изменение состояния газа графически можно изобразить адиабатой (1 ® 2). Для данной массы газа m согласно уравнению Пуассона (13) можно записать соотношение
(16)
Если сразу после открывания снова закрыть пробку 2, то давление внутри сосуда начнет возрастать от Р0 до Р2 вследствие того, что охладившийся при расширении воздух в сосуде станет снова нагреваться. Возрастание давления, которое происходит при постоянном объеме, прекратится, когда температура воздуха в сосуде сравняется с температурой окружающей среды (Т3 = Т1). Получим третье состояние газа (состояние 3).
Обозначим давление
воздуха в сосуде в этот момент через Р2
и соответствующее избыточное давление, которое установилось в сосуде при
нагревании воздуха от температуры Т2
до комнатной температуры Т1
через .
Тогда
(17)
Начальное 1 и конечное 3 состояния газа массы m наблюдаются при одинаковой температуре (Т3 = Т1), т.е. кривая 1-3 является изотермой. Поэтому на основании закона Бойля-Мариотта можно записать:
(18)
Возведя обе части уравнения (18) в степень g, получим
(19)
После того как уравнение (19) разделим на уравнение (16) и результат прологарифмируем, путем простых преобразований получим:
(20)
Поскольку и малы по сравнению с атмосферным давлением , то
и
можно разложить в ряд Тейлора по малым параметрам, ограничившись двумя первыми членами:
(21)
Подставляя (21) в (20), получим
(22)
Избыточное давление, определяемое по манометру, можно выразить соотношением
где h
– разность уровней жидкости в манометре, a – постоянный для данного
манометра коэффициент, зависящий от плотности жидкости и от площади сечения
трубок манометра.
Тогда можно записать, что
а
Подставив значения и в (22), получим формулу, удобную для расчета постоянной адиабаты
(23)
5. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ОБРАБОТКА
РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Перед тем как выполнять работу, проверьте, чтобы уровень воды в трубках U-образного манометра при открытой пробке 2 находился на половине высоты манометра. Если воды мало, долейте, попросив мерный стакан у лаборанта.
1. Пробкой 2 перекрыть отверстие в крышке баллона и открыть кран 3, соединяющий баллон с насосом 4.
2.
Вращая рукоятку насоса, осторожно накачивают воздух в баллон так,
чтобы разность уровней жидкости в трубках U-образного манометра составила 25 – 30 см.
3. Закрыть кран 3, разобщающий баллон и насос. Подождать 2-3 мин. пока жидкость не перестанет перетекать из одной трубки манометра в другую. При накачивании сжатый воздух в баллоне нагревается, поэтому необходимо выждать некоторое время, пока благодаря теплообмену температура в баллоне не станет равной комнатной. По шкале манометра измерьте установившуюся в конце изохорного охлаждения (состояние 1, см. рис. 3) разность уровней жидкости в обоих коленах манометра h1.
4.
На 2-3 секунды вынимают
пробку 2 в крышке баллона и выпускают из него часть воздуха. В
первые доли секунды происходит адиабатическое расширение газа (переход 1®2).
Пробку быстро ставят
на место, плотно закрывая баллон. Выждав 1-2 мин. пока газ, охлажденный при
адиабатическом расширении, нагреется до комнатной температуры, измеряют
разность уровней жидкости в коленах манометра h2 в конце изохорного нагревания (состояние 3, см.
рис. 3).
5. По формуле (23) вычисляют значение g.
6. Опыт повторяют 8 – 10 раз, причем для каждого опыта рассчитывают свое значение g, затем находят среднее арифметическое значение искомой величины по формуле:
где N – число измерений.
7. Вычисляют абсолютную Dg и относительную Е погрешности результата, исходя из истинного значения искомой величины:
и
Данные результатов
измерений и вычислений занесите в таблицу.
Таблица результатов
|
№ опыта |
h1 |
h2 |
g |
|
gтеор. |
Dg |
Е |
|
|
м |
м |
|
|
|
|
% |
|
|
|
|
|
|
1,4 |
|
|
6.
ВОПРОСЫ ДЛЯ ДОПУСКА К РАБОТЕ
- Какова цель работы?
- Опишите устройство рабочей установки и ход эксперимента.
3. Какой процесс называется адиабатическим? Какие условия соответствуют осуществлению адиабатического процесса на данной установке?
7. ВОПРОСЫ ДЛЯ ЗАЩИТЫ РАБОТЫ
1. Что называют удельной теплоемкостью вещества? Молярной теплоемкостью? Какая связь между ними?
2. Сформулируйте первый закон термодинамики.
3. Чему равны молярные теплоемкости идеальных газов при изопроцессах?
4. Докажите, что СР > CV.
5. Получите уравнение Пуассона для адиабатического процесса.
6. Что называется числом степеней свободы?
7.
Запишите выражение для внутренней энергии идеального газа и поясните
его.
8. Используя уравнение Пуассона, выведите рабочую формулу для расчета постоянной адиабаты g.
9. Из каких процессов состоит рабочий цикл, осуществляемый на данной установке при выполнении работы? Начертите график цикла.
Зависимость удельной теплоемкости от температуры при постоянном давлении
Удельная теплоемкость (C) — это количество теплоты, необходимое для изменения температуры единицы массы вещества на один градус.
- Изобарическая удельная теплоемкость (C p ) используется для воздуха в системе постоянного давления (ΔP = 0).
- I сохорическая удельная теплоемкость (C v ) используется для воздуха в постоянный объем , (= изоволюметрический или изометрический ) закрытая система.
Внимание! При нормальном атмосферном давлении 1,013 бар удельная теплоемкость сухого воздуха – C P и C V – зависит от температуры. Это может повлиять на точность расчетов процессов кондиционирования и обработки промышленного воздуха. При расчете массового и объемного расхода воздуха в обогреваемых или охлаждаемых системах с высокой точностью – удельная теплоемкость (= теплоемкость) должна быть скорректирована в соответствии со значениями, приведенными на рисунках и в таблице ниже, или найдена с помощью калькулятора.
- Для обычных расчетов – значение удельной теплоемкости c p = 1,0 кДж/кг K (равно кДж/кг o C) или 0,24 Btu(IT)/lb °F – обычно достаточно точный
- Для более высокой точности – значение Кл p = 1,006 кДж/кг К (равно кДж/кг o Кл) или 0,2403 БТЕ(ИТ)/фунт °F – better
Онлайн-калькулятор удельной теплоемкости воздуха
Приведенный ниже калькулятор можно использовать для оценки удельной теплоемкости воздуха при постоянном объеме или постоянном давлении и при заданных температуре и давлении.
Выходная теплоемкость выражается в виде кДж/(кмоль*К), кДж/(кг*К), кВтч/(кг*К), ккал/(кг*К), БТЕ(ИТ)/(моль*°Р ) и БТЕ(ИТ)/(фунт м *°R)
Температура
Выберите фактическую единицу измерения температуры: °C °F K °R
Выберите фактическое давление: 1 бар абс. 14,5 фунтов на квадратный дюйм; 10 бар абс. / 145 фунтов на кв. дюйм абс.; 50 бар абс. / 725 фунтов на кв. дюйм абс.; 100 бар абс. / 1450 фунтов на кв. дюйм абс.;
См. также другие свойства Воздух при различной температуре и давлении: Плотность и удельный вес при различной температуре, Плотность при различном давлении, Коэффициенты диффузии газов в воздухе, Число Прандтля, Удельная теплоемкость при различном давлении, Теплопроводность, Температуропроводность, Свойства в условиях газожидкостного равновесия и Теплофизические свойства воздуха при стандартных условиях и Состав и молекулярная масса,
, а также Удельная теплоемкость аммиака, бутана, диоксида углерода, монооксида углерода, этана, этанола, этилена, водорода, метана, метанола, азота, кислорода, пропана и воды.
Назад к вершине
Верхне
Вверх теплоемкость – поворота экрана!
| Температура | Изохорная теплоемкость (Cv) | Изобарическая теплоемкость (Cp) 9 9 03207
Вернуться к началу Преобразование единиц измерения: Преобразователь единиц удельной теплоемкости = [°F], кельвин = [K], градусный разряд = [°R], джоуль = [Дж], килокалория (Международная таблица) = [ккал (ИТ)], килограмм = [кг], килоджоуль = [кДж] , киловатт-час = [кВтч], моль = [моль], фунт = [фунт] K в единицах можно заменить на °C, и наоборот. °R в единицах можно заменить на °F и наоборот.
Вернуться к началу Удельная теплоемкость в зависимости от давления при постоянной температуре Удельная теплоемкость (C) количество тепла, необходимое для изменить температуру единицы массы вещества на один градус.
Удельная теплоемкость сухого воздуха – С P и C V – зависит от давления и температуры. Это может повлиять на точность расчетов процесса обработки промышленного воздуха. При расчете массового и объемного расхода воздуха в обогреваемых или охлаждаемых системах с высокой точностью – удельная теплоемкость (= теплоемкость) должна быть скорректирована в соответствии со значениями на рисунках и в таблице ниже. См. также другие свойства Воздух при различных температурах и давлениях: Плотность и удельный вес при различных температурах, Плотность при различных давлениях, Коэффициенты диффузии газов в воздухе, Число Прандтля, Удельная теплоемкость при различных температурах, Теплопроводность, Температуропроводность, свойства в условиях газожидкостного равновесия и теплофизические свойства воздуха в стандартных условиях и состав и молекулярная масса, Удельная теплоемкость сухого воздуха при постоянной температуре 20 o C / 68°F при различных давлениях: Для полной таблицы с изохлорной теплоемкостью – поверните экран!
1) Стандартная атмосфера Преобразование единиц измерения: Британская тепловая единица (Международная таблица) = [BTU(IT)], градус Цельсия = [°C], градус Фаренгейта = [°F], градус Кельвина = [K], градус ранкина = [° Р], джоуль = [Дж], килокалория (Международная таблица) = [ккал(ИТ)], килограмм = [кг], килоджоуль = [кДж], киловатт-час = [кВтч], моль = [моль], фунт = [фунт ] K в единицах измерения можно заменить на °C, и наоборот. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
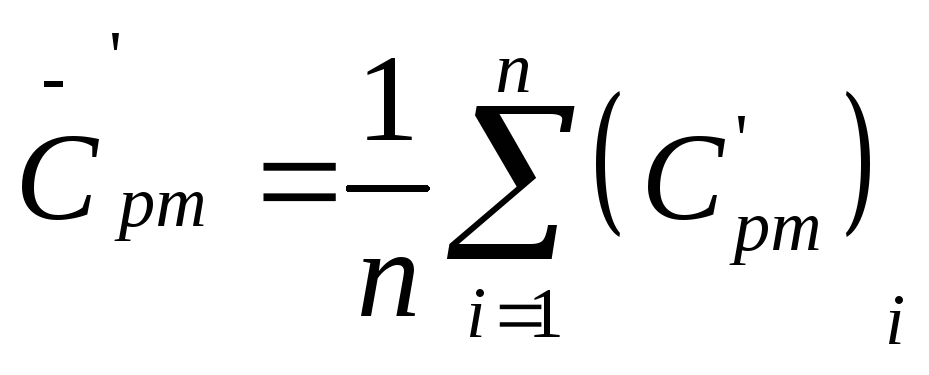
03398
040
24147
02075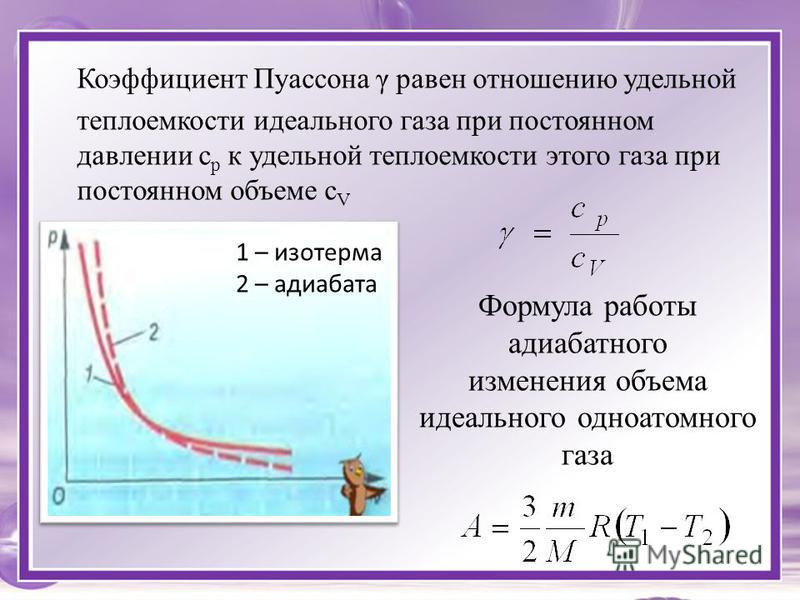
0127
02923
02150
000305
9535
/(фунт °F)] 
2401
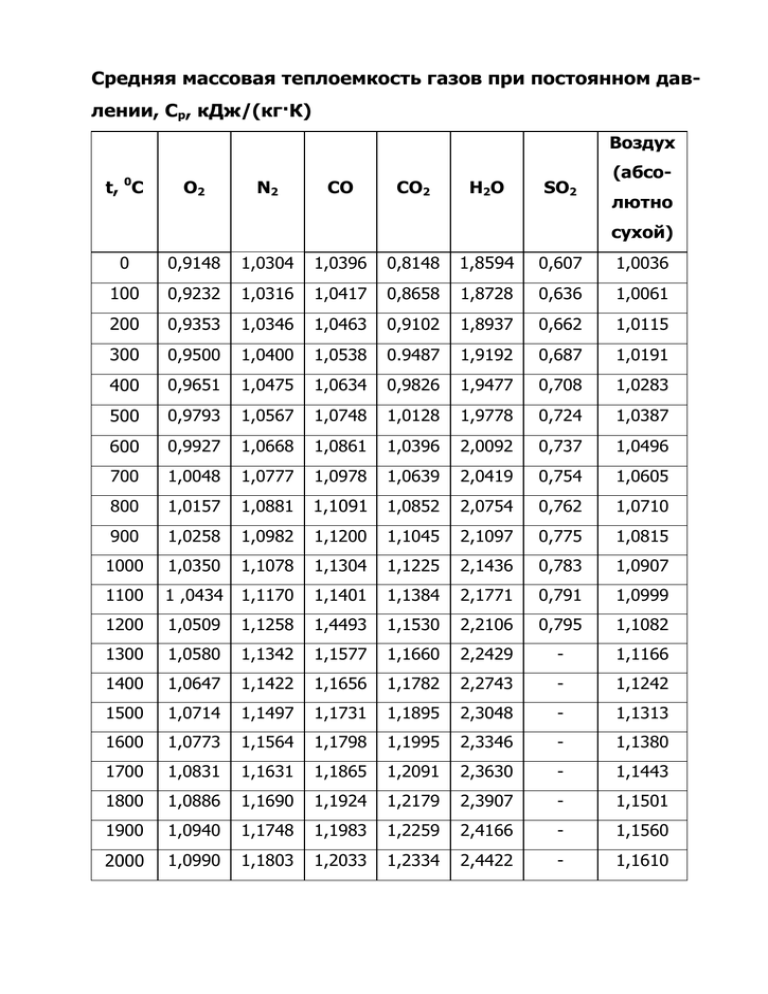2569