39. Уравнения Гендерсона Гассельбаха для расчёта рН буферных систем (вывод).
Уравнение показывает как зависит кислотно-основное равновесие буферного раствора от свойств компонентов кислотно-основной буферной системы и от количественного соотношения этих компонентов в растворе. Показателем кислотно-основного равновесия в растворе является водородный показатель, pH. Свойство кислоты (её способность распадаться на ионы), как составляющей буферной системы, характеризуется значением константы равновесия, константы диссоциации кислоты, Ka. (или в логарифмической форме pKa = – lgK, в частности, если K = 10–11, то pK = 11). Количественая структура (состав) буферной системы может быть оценена в виде отношения соль/кислота (эквиваленты, эквивалентная масса). Учитывая сказанное, уравнение Гендерсона-Гассельбаха выглядит следующим образом:
pH = pKa + lg (соль/кислота).
С
помощью этого уравнения можно оценить
любую из его переменных,
если известны две другие. Например,
эквивалентная, или нормальная концентрация HCO3
Например,
эквивалентная, или нормальная концентрация HCO3
pH = 6,1 + lg (26 / 1,3), pH = 7,4.
40. Буферные системы крови.
Бу́ферные систе́мы кро́ви (от англ. buffer, buff — смягчать удар) — физиологические системы и механизмы, обеспечивающие заданные параметры кислотно-основного равновесия в крови[1]. Они являются «первой линией защиты», препятствующей резким перепадам pH внутренней среды живых организмов.
Циркулирующая кровь представляет собой взвесь живых клеток в жидкой среде, химические свойства которой очень важны для их жизнедеятельности. У человека за норму принят диапазон колебаний pH крови 7,37-7,44 со средней величиной 7,4. Буферные системы крови слагаются из буферных систем плазмы и клеток крови и представлены следующими системами:
бикарбона́тная бу́ферная систе́ма;
фосфа́тная бу́ферная систе́ма;
белко́вая бу́ферная систе́ма;
гемоглоби́новая бу́ферная систе́ма.

41. Методы получения коллоидных растворов.
Коллоидной системой (золем) называется гетерогенная система, в которой одна из фаз представлена мелкими частицами, равномерно распределёнными в объёме другой однородной фазы. Это ультрамикрогетерогенные системы, состоящие из частиц дисперсной фазы – совокупности раздробленных частиц, размер которых лежит в пределах 10-9 м – 10-5 м, и непрерывной дисперсионной среды, в которой распределены эти частицы.
Для получения коллоидных растворов необходимо:
достичь коллоидной степени дисперсности;
подобрать дисперсионную среду, в которой нерастворимо вещество дисперсный фазы;
подобрать третий компонент – стабилизатор, сообщающий коллоидной системе устойчивость. В качестве стабилизаторов используют вещества, препятствующие агрегации (слипанию) коллоидных частиц в более крупные и выпадению их в осадок (небольшой избыток одного из реагентов, из которых получается вещество дисперсной фазы; ПАВ; белки; полисахариды).

Уравнение Гендерсона-Гассельбаха — Студопедия
Поделись с друзьями:
Для кислотного буферного раствора;
Для основного буферного раствора;
Где Са(Сb)-концентрация раствора кислоты(основания)
Cs-концентрация раствора соли
Va(Vb) –объем раствора кислоты(основания)
Vs-объем раствора соли
=-lgKa – кислотный показатель
=-lgKb – основной показатель
Буферная ёмкость– это величина характеризующая способность буферного раствора противодействовать изменению реакции среды при добавлении сильных кислот или сильных оснований.

Ca- концентрация эквивалента сильной кислоты
Va- объем добав. сильной кислоты
Факторы влияющие на буферную емкость раствора
1) Концентрация компонентов
2) Отношение концентрации компонентов
При разбавлении буферная емкость уменьшается чем больше концентрация компонентов буфера тем больше буферная емкость.
Самой большой буферной емкостью и по кислоте и по щелочи обладает буферная система, когда соотношение компонентов =1.
Белковая буферная система – главный внутриклеточный буфер. Он составляет примерно 3 четверти буферной емкости внутриклеточной жидкости.
Компонентами белкового буфера явл-сяслабодисациирующий белок с кислыми св-ми (белок СООН) и соли сильного основания (белок COONa).При нарастании уровня кислот они взаимодействуют с солью белка с образованием нейтральной соли и слабой кислоты. При увеличении концентрации оснований реакция их происходит с белком с кислыми св-ми. В рез-те вместо сильного основания образуется слабоосновная соль.

Гемоглобиновая буферная система{HHb«H++Hb–; KHb«K++Hb– обладает самой большой величиной буферной емкости. Действует в эритроцитах крови. Ее буферная емкость (b) составляет 75% от всей буферной емкости крови.
Оксигемоглобиновая буферная система {HHbO2«H++HbO2–; KHbO2«K++HbO2– имеет такую же величину буферной емкости, как и гемоглобиновая буферная система.
Эфиры глюкозы и фосфорной кислоты различной степени замещения {Г-PO3Na2; Г-PO3NaH. Она способствует сохранению постоянства pH в организме.

В медицине кислотно-щелочное равновесие организма оценивают с помощью уравнения Гендерсона-Гассельбаха, выведенного для карбонатного буфера:
pH=pK+lg([HCO3–]/[H2CO3]).
Опытным путем было найдено, что в крови здорового человека pK=6,11 и pH=7,34-7,36, рабочая формула крови человека: pH=6,11+lg([HCO3–]/[CO2]).
Т.е., благодаря буферному действию вышеуказанных систем pH крови в норме практически не меняется, несмотря на поступление извне значительных количеств сильных кислот и щелочей.
Ацидоз-смещение кислотно-щелочного баланса организма в сторону увеличения кислотности.Алкалоз-увеличение рН крови за счет накопления щелочных веществ.
Щелочной резерв крови: представляет собой объем(мл) химически связанного диоксида углерода СО2 (главным образом в виде гидрокарбонатов) в 100 мл плазмы крови; измеряется в объемных процентах; в норме составляет 50-70 объемных процентов (25-30 моль/л).

2)))a-аминокислоты можно рассматривать как производные карбоновых кислот, в молекулах которых один из атомов водорода замещен аминогруппой (NH2). Общее число АК достигает 300, но из них выделяют группу 20-ти наиболее важных a-АК, встречающихся в составе белков животного и растительного происхождения.
Для аминокислот характернастереоизомерия. Асимметричным является a-углеродный атом, т.к. с ним связаны четыре различные химические группы, в этом случае для каждой a-аминокислоты существует две возможные конфигурации – D- и L-энантиомеры. В белках встречаются только L-изомеры a-аминокислот. Это имеет важнейшее значение для формирования пространственной структуры белков и проявления ими биологической активности. С этим непосредственно связанастереоспецифичность действия ферментов.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Уравнение Хендерсона-Хассельбальха | ChemTalk
Учебные пособия
- Сообщение от Сесилия Фоллбрехт
01
декабря Основные понятияВ этом учебном пособии вы узнаете, что такое уравнение Хендерсона-Хассельбаха, как использовать уравнение для определения pH буфера, как вывести уравнение и как решить некоторые примеры задач
Что такое уравнение Хендерсона-Хассельбаха?Уравнение Хендерсона-Хассельбаха используется для определения pH буферной системы.
K a представляет собой константу диссоциации кислоты, а pKa представляет собой отрицательный логарифм K a . [Сопряженная основа] также обычно пишется как [A-]. И [Слабая кислота] может рассматриваться как [HA]. Эти значения относятся к равновесной концентрации.
Если у вас одинаковая концентрация кислоты и сопряженного основания, то pH будет таким же, как pK a , потому что log(1) = 0.
Если [HA] = [A – ], то
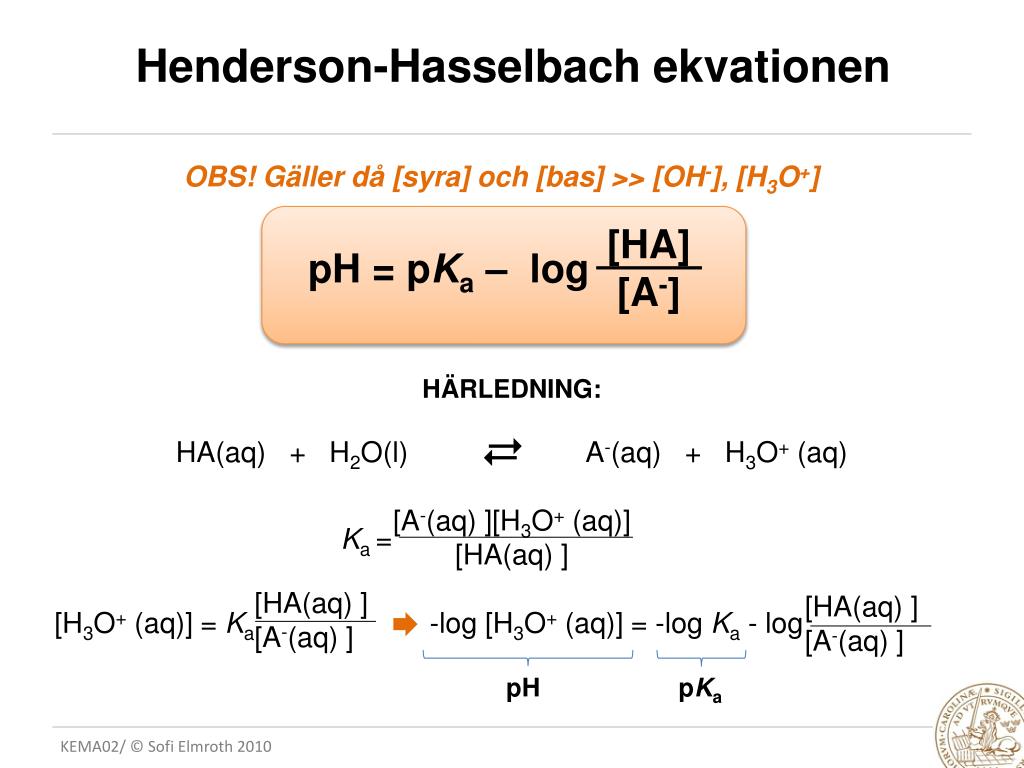
Вывод уравнения Хендерсона-ХассельбахаУравнение Хендерсона-Хассельбаха можно получить из уравнения K a слабой кислоты.
 Здесь мы предположим, что у нас есть слабая кислота HA и сопряженное с ней основание A – . В воде происходит следующая диссоциация:
Здесь мы предположим, что у нас есть слабая кислота HA и сопряженное с ней основание A – . В воде происходит следующая диссоциация:Следовательно, константа диссоциации кислоты определяется как
, которую можно преобразовать в
Затем возьмите журнал с обеих сторон.
Умножьте на -1, чтобы на следующем шаге мы могли заменить pH.
Основываясь на определении pH = -log [H 3 O + ] мы можем подставить в наше уравнение
И затем использовать правила логарифмирования для упрощения правой части
Зная, что pK a = -log (K a ), мы можем подставить это в наше предыдущее уравнение, чтобы получить уравнение Хендерсона-Хассельбальха
Примеры задач уравнения Хендерсона-ХассельбалхаОпределение буферного соотношения
Предположим, мы готовим буферный раствор аммония (NH 4 + ) и аммиака (NH 3 ). В этом примере аммоний — наша слабая кислота, а аммиак — сопряженное основание.
 Реакция следующая.
Реакция следующая.Если pK a аммония составляет 9,3, а мы хотим, чтобы pH был равен 10. Какое соотношение аммиака к аммонию следует добавить в раствор?
Проблема требует отношения, поэтому мы ищем значение или для этого конкретного буферного раствора. Чтобы решить проблему, начните с подстановки известных значений – pH и pK 9.0027 и .
Вычтите 9,3 с каждой стороны, чтобы упростить
Искомое отношение находится в пределах логарифмического члена. Чтобы избавиться от журнала, мы можем использовать логарифмические правила для упрощения.
Таким образом, отношение примерно в 5 раз превышает количество аммиака по сравнению с аммонием, чтобы получить буферный раствор с рН 10.
Определение рН 0,15 М CH
3 COO – и 0,20 М CH 3 COOH. pKa уксусной кислоты (CH 3 COOH) составляет 4,75.Чтобы решить эту примерную задачу, мы хотим начать с уравнения Хендерсона-Хассельбаха, поскольку мы рассматриваем буферный раствор слабой кислоты и сопряженного основания.

Затем подставьте известные значения в наше уравнение
Затем упростите и решите
Наш буферный раствор уксусной кислоты имеет рН 4,63.
Ограничения уравнения Хендерсона-Хассельбаха- При использовании Henderson-Hasselbalch для приготовления буферного раствора соотношение [A – ]/[HA] должно быть близко к единице. Это наиболее стабильное решение. Когда отношение далеко от единицы, буферная способность раствора уменьшается, так как незначительное возмущение резко изменяет рН.
- Это уравнение pH не учитывает самодиссоциацию воды. При очень низких концентрациях буфера вода может вносить вклад в pH
- Если кислота может легко диссоциировать более одного иона гидроксония (H + ) уравнение не учитывает это и может работать некорректно.
- На практике при создании буферов с определенным pH важно, чтобы pK и были близки к целевому pH, чтобы иметь самый широкий диапазон буферных свойств.

- Уравнение названо в честь Лоуренса Джозефа Хендерсона и Карла Альберта Хассельбальха. Хендерсон составил исходное уравнение в 1908 году. Затем, в 1917 году, Хассельбальх представил формулу в логарифмическом виде, и так, как это наиболее часто встречается сегодня.
- Уравнение Хендерсона-Хассельбальха имеет важное биологическое значение. Многие биологические образцы должны храниться при определенном значении pH. Таким образом, при подготовке образцов уравнение Хендерсона-Хассельбаха используется для приготовления буфера, который поможет белкам и другим молекулам, чувствительным к рН, сохранить свою структуру.
- Уравнение также можно написать для pOH буферной системы.
[Конъюгированная кислота] также упоминается как [HB + ]. И [Слабое основание] также упоминается как [B]. Попробуйте проверить свое понимание, выполнив вывод уравнения для pOH.
Приближение Хендерсона-Хассельбальха — Химия LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1298
- Молярность буфера(ов) должна быть в 100 раз больше, чем константа кислотной ионизации, или K a .
- Это уравнение даст плохие или неточные результаты, если присутствуют сильные кислоты или основания. Значения pK a между 5 и 9 дадут хорошие приближения, но когда мы выходим за пределы этого диапазона, существует большая вероятность того, что значение pH будет неправильным.

Приближение Хендерсона-Хассельбальха позволяет нам одним методом приблизить рН буферного раствора. Основное уравнение выглядит следующим образом: 9-]}{[HA]} \номер\]
Основное уравнение выглядит следующим образом: 9-]}{[HA]} \номер\]
У нас есть простые расчеты для сильных кислот и оснований, но вычисления для буферов довольно сложны и требуют много времени. Использование того факта, что слабые кислоты и основания почти не ионизируются, позволяет нам приблизить рН буферных растворов, используя начальные концентрации. Хотя аппроксимация имеет несколько ограничений, она упрощает длительные вычисления до простого уравнения, полученного из \(K\).
Лоуренс Джозеф Хендерсон и Карл Альберт Хассельбальх
Лоуренс Джозеф Хендерсон (1878-1942) был талантливым биохимиком, среди многих других титулов, который провел большую часть своей карьеры в Гарварде. Он отвечал за разработку компонентов уравнения после изучения равновесных реакций, происходящих в крови в результате дыхания (специализируясь на «усталости»). Его уравнение было бы неполным без основательных расчетов, сделанных Хассельбальхом.
Карл Альберт Хассельбальх (1874-1962) был химиком, внимательно изучавшим рН.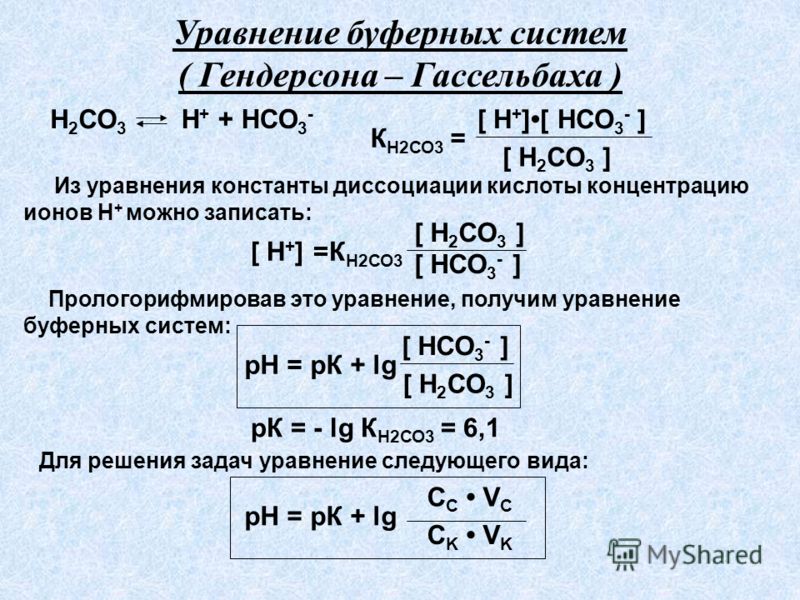 Он также изучал кровь и реакции, протекающие с кислородом, если говорить проще. В конце концов он модифицировал уравнение Хендерсона, поставив математическое 9{−5}) = 4,756\номер \]
Он также изучал кровь и реакции, протекающие с кислородом, если говорить проще. В конце концов он модифицировал уравнение Хендерсона, поставив математическое 9{−5}) = 4,756\номер \]
\[pH = pK_a + \log_{10} \left( \dfrac{[ацетат]}{[\text{уксусная кислота}] + [HCl]} \right )\nonumber \]
обратите внимание, что молярное соотношение также работает вместо концентраций, поскольку и кислота, и основание находятся в одном растворе
\[pH = 4,756 + \log_{10} (0,588)\nonumber \]
\[рН = 4,756 – 0,230 = 4,52\нечисло \]
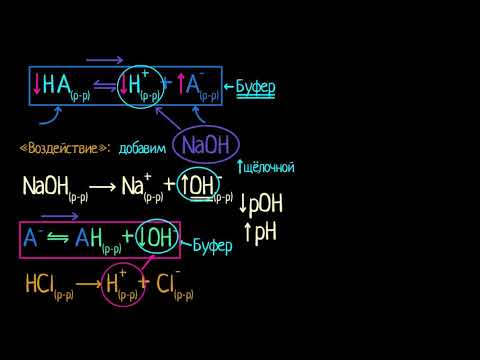




 Здесь мы предположим, что у нас есть слабая кислота HA и сопряженное с ней основание A – . В воде происходит следующая диссоциация:
Здесь мы предположим, что у нас есть слабая кислота HA и сопряженное с ней основание A – . В воде происходит следующая диссоциация: Реакция следующая.
Реакция следующая.

