Изменение температуры воды p в баке как функции времени t – Изменение температуры воды p (°С) в баке как функции времени t (мин) описано с помощью формул: p = {2t + 20, если 0

Изменение температуры – Справочник химика 21

    Температурный коэффициент скорости реакции показывает, во сколько раз изменится константа скорости реакции при изменении температуры иа 10° С. [c.268]

    Чем меньше масло меняет свою вязкость при изменении температуры, или, другими словами, чем по-ложе вязкостно-температурная кривая, тем выше качество масла. Это объясняется тем, что масло с пологой кривой вязкости при высоких температурах сохраняет достаточную вязкость для надежной смазки деталей двигателя, а при низких температурах вязкость такого масла не настолько велика, чтобы затруднить запуск двигателя и прокачку масла по трубопроводам. В спецификации на масла приводятся вязкости минимум при двух температурах и данные о пологости вязкостнотемпературной кривой или в виде величины отношения кинематической вязкости при низкой температуре (50° С) к вязкости масла при высокой температуре (100° С), или в виде индекса вязкости. [c.155]

    С понижением температуры топлива увеличивается его вязкость и плотность. Изменение вязкости в зависимости от изменения температуры топлив показано на рис. 29. Вязкость топлив оказывает большое влияние на прокачиваемость топлива и в особенности на качество его распыления.  [c.52]

    На основе гидродинамической теории можно рассчитать радиусы мигрирующих иоиов поскольку ири этом используется уравнение Стокса (5.4), они называются стоксовыми радиусами. Стоксо-выс радиусы обычно заметно больше кристаллохимических, иными словами, мигрируют гидратированные ионы. Из уравнения (5.9), вытекающего из гидродинамической теории, можно получить эмпирическое правило Вальдена — Писаржевского, если допустить, что прн изменении температуры или природы растворителя размеры ионов (стоксовы радиусы) остаются постоянными. Обычно это условие не выполняется, чем и объясняется приближенный характер правила Вальдена — Писаржевского. [c.120]

    Гиббс разработал простое уравнение, правило фаз, позволяющее предсказать характер изменения температуры, давления и коицентрации различных компонентов при различных сочетаниях числа компонентов и фаз. [c.114]

    Чтобы вычислить равновесный состав, достигаемый в адиабатических условиях, следует найти изменение температуры со степенью полноты реакции. Энтальпия единицы объема реагирующей смеси равна [c.54]

    Центрами кристаллизации выделяющейся воды могут быть кристаллы углеводородов и частицы механических примесей. Выделяющаяся из топлива вода при изменении температуры, влажности или атмосферного давления находится в виде эмульсии воды с топливом. Эмульсия воды в топливе может образоваться также при нарушении правил транспортировки, хранения, перекачки, когда в топливо попадает свободная вода. Эмульсию воды с топливом очень трудно обнаружить и удалить из топлива, поэтому она представляет большую опасность для нормальной работы систем и агрегатов летательного аппарата. Эмульсия — это, как известно, смесь двух жидкостей, где одна жидкость распределена в другой в виде мельчайших капелек. Размеры капелек воды в водо-топливных эмульсиях находятся в пределах 10—40 мк. 

[c.50]

    Номограмма Билла составлена для вычисления давления ня-сыщенных паров в интервале от 1,33 Па до 13 МПа углеводородов и узких нефтяных фракций с температурой кипения от 100 до 1000 °С в интервале изменения температур системы от 100 до 500 °С. Средняя относительная погрешность уравнений равна +2%, максимальная 5%. [c.41]

    Изменение температуры определяется видом кинетической кривой, т. е. кривой зависимости скорости реакции от времени, поскольку выделение или поглощение тепла примерно пропорционально количеству прореагировавшего продукта. [c.263]

    Конденсация влаги из воздуха вследствие изменения температуры может происходить не только на металлических стенках топливных, баков, но и на поверхности охлажденного топлива. Причем влага, конденсирующаяся на поверхности топлива, не замерзает сразу, а вначале растворяется или в виде взвеси распространяется в топливе. 

[c.50]

    Математическое выражение для онределения температуры, эквивалентной средней скорости неизотермических процессов, выведено в предположении, что изменение температуры процесса является прямолинейным. При небольших перепадах температур такое допущение не дает заметных погрешностей. В случае же больших перепадов температур зону реакции разбивают на ряд участков, на каждом из которых принимают прямолинейное изменение температуры. [c.270]

    Гигроскопичность жидкости называется необратимой, если поглощаемая жидкостью вода при изменении температуры и влажности не выделяется в виде самостоятельной

www.chem21.info

Расчеты ГВС, БКН. Находим объем, мощность змейки, время прогрева и т.п.

Расчеты ГВС, БКН. Находим объем, мощность ГВС, мощность БКН(змейки), время прогрева и т.п.

В этой статье рассмотрим практические задачи для нахождения объемов накопления горячей воды, мощности нагрева ГВС. Мощности нагревательного оборудования. Время готовности горячей воды для различного оборудования и тому подобное.

Какие схемы использовать для получения ГВС? Ответ тут: Схемы получения ГВС у котла.

Рассмотрим примеры задач:

1. Расчет мощности проточного водонагревателя 2. Расчет выходной температуры у проточного водонагревателя 3. Расчет время нагрева электрического водонагревателя (бойлера) 4. Расчет времени нагрева бойлера косвенного нагрева 5. Сколько необходимо накопить горячей воды для того, чтобы помыться 30 минут в душе? 6. Расчет объема бака на ГВС 7. Расчет дополнительной мощности на ГВС. Мощность котла = Отопление + ГВС

Задача 1. Найти мощность проточного водонагревателя

Проточный водонагреватель – это водонагреватель объем воды, в котором может быть настолько мал, что его существование бесполезно для накопления воды. Поэтому считается, что проточный водонагреватель не предназначен аккумулировать горячую воду. И мы это не учитываем в расчетах.

Дано: Расход воды равен 0,2 л/сек. Температура холодной воды 15 градусов Цельсия.

Найти: Мощность проточного водонагревателя, при условии, что он нагреет воду до 45 градусов.

Решение

Как найти теплоемкость при различных температурах воды описано тут: http://infobos.ru/str/576.html

Ответ: Мощность проточного водонагревателя составит 25120 Вт = 25 кВт.

Практически не целесообразно потреблять большое количество электроэнергии. Поэтому необходимо аккумулировать(накапливать горячую воду) и уменьшать нагрузку на электропровода.

Проточные водонагреватели имеют не стабильный прогрев горячей воды. Температура горячей воды будет зависеть от расхода воды через проточный водонагреватель. Датчики переключения мощности или температуры не позволяют хорошо стабилизировать температуру.

Если хотите найти выходную температуру существующего проточного водонагревателя при определенном расходе.

Задача 2. Время нагрева электрического водонагревателя (бойлера)

Имеем электрический водонагреватель объемом 200 литров. Мощность электрических тэнов 3 кВт. Необходимо найти время нагрева воды с 10 градусов до 90 градусов Цельсия.

Дано:

Wт = 3кВт = 3000 Вт.

Найти: Время, за которое объем воды в баке водонагревателя нагреется с 10 до 90 градусов.

Решение

Потребляемая мощность тэнов не меняется от температуры воды в баке. (Как меняется мощность в теплообменниках, рассмотрим в другой задаче.)

Необходимо найти мощность тэнов, как для проточного водонагревателя. И этой мощности будет достаточно нагреть воду за 1 час времени.

Если известно, что с мощностью тэнов в 18,6 кВт бак нагреет воду за 1 час времени, тогда не сложно посчитать время с мощностью тэнов на 3 кВт.

Ответ: Время нагрева воды с 10 до 90 градусов с емкостью 200 литров составит 6 часов 12 минут.

Далее рассчитаем время нагрева бойлера косвенного нагрева.

Задача 3. Время нагрева бойлера косвенного нагрева

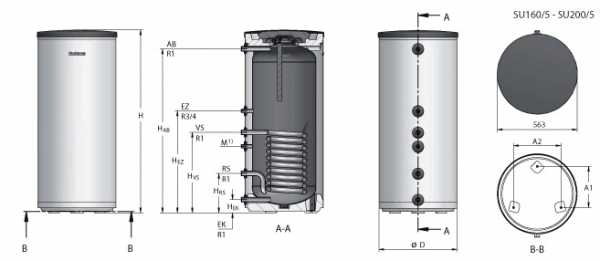
Рассмотрим для примера бойлер косвенного нагрева: Buderus Logalux SU200

Номинальная мощность: 31.5 кВт. Тут не понятно, из каких соображений это найдено. Но посмотрите таблицу ниже.

Объем 200 литров

Змейка сделана из стальной трубы DN25. Внутренний диаметр 25 мм. Наружный 32 мм.

Гидравлические потери в трубе-змейке указывают 190 мБар при расходе 2 м3/час. Что соответствует 4.6 Kvs.

Конечно, это сопротивление велико для воды и новой трубы. Скорее всего были заложены риски на зарастание трубопровода, на теплоноситель с большой вязкостью и сопротивление на соединениях. Лучше указать заведомо большие потери, чтобы кто-либо не просчитался в расчетах.

Расчет гидравлических потерь в трубе

Что такое Kvs?

Зарастание трубопроводов

Площадь теплообмена 0,9 м2.

Помещается в трубу-змейку 6 литров воды.

Длина этой трубы-змейки примерно 12 метров.

Время прогрева пишут 25 минут. Тут не понятно, как это посчитали. Смотрим таблицу.

Таблица мощности змейки БКН

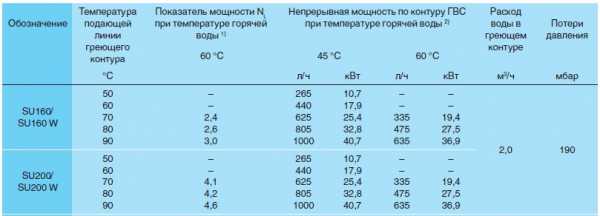
Рассмотрим таблицу определения мощности змейки

Рассмотрим SU200 мощность теплоотдачи змейки 32,8 кВт

Затекает в змейку теплоноситель с температурой 80 градусов с расходом 2 м3/час.

При этом в контуре ГВС расход 805 л/час. Затекает 10 градусов выходит 45 градусов

Другой вариант

Рассмотрим SU200 мощность теплоотдачи змейки 27,5 кВт

Затекает в змейку теплоноситель с температурой 80 градусов с расходом 2 м3/час.

При этом в контуре ГВС расход 475 л/час. Затекает 10 градусов выходит 60 градусов

Другие характеристики

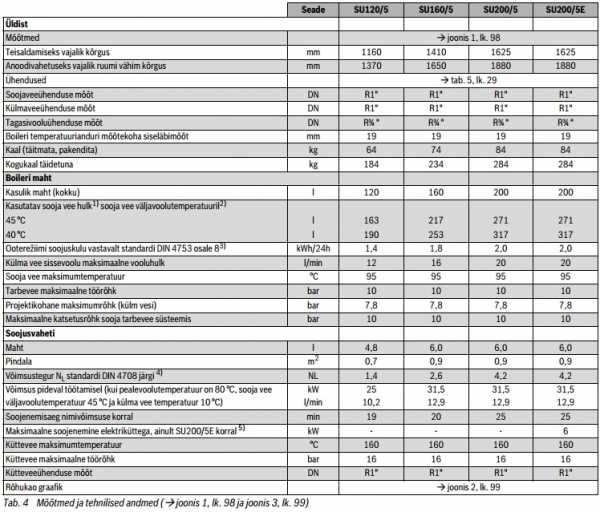
К сожалению, я Вам не предоставлю расчет времени нагрева бойлера косвенного нагрева. Потому что это не одна формула. Тут переплетения множество значений: Начиная от формул коэффициента теплопередачи, поправочные коэффициенты для разных теплообменников (так как конвекция воды тоже вносит свои отклонения), и заканчивается это итерацией расчетов по измененным температурам с течением времени. Тут, скорее всего в будущем я сделаю калькулятор расчета.

Вам придется довольствоваться тем, что нам говорит производитель БКН(Бойлера косвенного нагрева.)

А говорит нам производитель следующее:

Что вода будет готова через 25 минут. При условии, что затекать в змейку будет 80 градусов с расходом 2 м3/час. Мощность котла, дающий нагретый теплоноситель не должна быть ниже 31,5 кВт. Готовая к приему вода считается 45-60 градусов. 45 градусов помыться в душе. 60 это очень горячая вода, например для мыться посуды.

Задача 4. Сколько необходимо накопить горячей воды для того, чтобы помыться 30 минут в душе?

Рассчитаем для примера с электрическим водонагревателем. Так как электрический тэн имеет постоянную отдачу тепловой энергии. Мощность тэнов 3 кВт.

Дано:

Холодная вода 10 градусов

Минимальная температура из крана 45 градусов

Максимальная температура нагрева воды в баке 80 градусов

Комфортный расход вытекающей воды из крана 0,25 л/сек.

Решение

Сначала найдем мощность, которая обеспечит данный расход воды

Ответ: 0,45 м3 = 450 литров воды понадобится для того, чтобы помыться накопленной горячей водой. При условии, что тэны не нагревают воду в момент потребления горячей воды.

Многим может показаться, что нет учета входа холодной воды в бак. Как рассчитать потерю тепловой энергии, когда в воду 80 градусов попадает температура воды 10 градусов. Явно будет идти потеря тепловой энергии.

Это доказывается следующим образом:

Энергия, затраченная на нагрев бака с 10 до 80:

То есть в баке объемом 450 литров с температурой 80 градусов уже содержится 36 кВт тепловой энергии.

Из этого бака мы забираем энергию: 450 литров воды с температурой 45 градусов (через кран). Тепловая энергия воды объемом 450 литров с температурой 45 градусов = 18 кВт.

Эта доказывается законом сохранения энергии. Изначально в баке было 36 кВт энергии, забрали 18 кВт осталось 18 кВт. Эти 18 кВт энергии содержат воду с температурой 45 градусов. То есть 70 градусов поделили пополам получили 35 градусов. 35 градусов + 10 градусов холодной воды получаем температуру 45 градусов.

Тут главное понять, что такое закон сохранения энергии. Эта энергия из бака не может убежать не понятно куда! Мы знаем, что через кран вышло 18 кВт, а в баке изначально был 36 кВт. Забрав у бака 18 кВт мы понизим температуру в баке до 45 градусов (до средней температуры (80+10)/2=45).

Давайте теперь попробуем найти объем бака при нагреве бойлера до 90 градусов.

Использованная энергия потребления горячей воды на выходе из крана 18317 Вт

Ответ: Объем бака 350 литров. Повышение всего на 10 градусов уменьшило объем бака на 100 литров.

Многим может показаться это не реально. Это можно объяснить следующим образом: 100/450 = 0,22 это не так уж и много. Разница сохраненной температуры (80-45)

Докажем, что это справедливая формула другим способом:

Конечно это грубый теоретический расчет! В теоретическом расчете мы учитываем то, что температура в баке между верхним и нижним слоем мгновенно перемешивается. Если учитывать факт того, что вверху вода горячее, а внизу холоднее, то объем бака можно уменьшить на разницу температур. Не зря вертикальные баки считаются более эффективными по сохранению тепловой энергии. Так как чем больше высота бака, тем выше разница температур между верхним и нижним слоем. При быстром расходовании горячей воды, эта разница температур выше. Когда расхода воды нет, очень медленно температура в баке становится равномерной.

Попробуем пересчитать, если между верхним и нижним слоем воды разница будет 10 градусов.

Мы просто 45 градусов спустим на 10 градусов ниже. За место 45 будет 35 градусов.

Ответ: За счет смещения температур мы уменьшили объем бака еще на 0,35-0,286=64 литра.

Мы рассчитали при условии, что в момент потребления горячей воды тэны не работали и не нагревали воду.

Давайте теперь посчитаем при условии, что бак начинает нагревать воду в момент потребления горячей воды.

Добавим еще мощности 3 кВт.

За 30 минут работы мы получим половину мощности 1,5 кВт.

Тогда нужно вычесть эту мощность.

Ответ: Объем бака составит 410 литров.

Задача 5. Расчет дополнительной мощности на ГВС

Рассмотрим частный дом площадью 200 м2. Максимальное потребление мощности на обогрев дома 15 кВт.

Как найти мощность на отопление дома?

Проживают в доме 4 человека.

Найти: Дополнительную мощность для ГВС

То есть нам необходимо найти мощность котла с учетом: Мощности обогрева дома + нагрев горячей воды.

Для этой цели лучше использовать схему № 4: http://infosantehnik.ru/str/102.html

Решение

Необходимо найти, сколько литров горячей воды потребляет человек в сутки:

В СНиП 2.04.01-85* указано, что по статистике на одного человека уходит 300 литров в сутки. Из них 120 литров на горячую воду с температурой 60 градусов. Это городская статистика перемешена с людьми, которые не привыкли тратить столько воды в сутки. Могу предложить свою статистику потребления: Если Вы любите принимать горячие ванны каждый день – Вы можете расходовать 300-500 литров горячей воды в сутки только на одного человека.

Объем воды в сутки на 4 человека:

То есть к мощности обогрева дома 15 кВт необходимо прибавить 930 Вт.=15930 Вт.

Но если учитывать факт того, что ночью (с 23:00 – 7:00) вы не потребляете горячую воду, то получится 16 часов, когда Вы потребляете горячую воду:

Ответ: Мощность котла = 15 кВт + 1,4 кВт на ГВС. = 16,4 кВт.

Но в таком расчете есть риск, того, что в момент большого потребления горячей воды в определенные часы вы надолго остановите обогрев дома.

Если хотите иметь хороший расход горячей воды для частного дома, то выбираем БКН не менее 30 кВт. Это позволит Вам иметь неограниченный расход 0,22 л/сек. с температурой минимум 45 градусов. Мощность котла при этом не должна быть меньше 30 кВт.

А вообще в задачах этой статьи был уклон на сохранение энергии. Мы не рассматривали, что происходит в конкретный момент, а пошли для расчета другим путем. Мы пошли по бесспорному методу сохранения энергии. Затраченная энергия на выходе из крана потом будет равна энергии приходящей от котлового оборудования. Зная мощности в двух разных местах можно найти затраченное время.

Однажды обсуждали расчет ГВС на форуме: http://santeh-baza.ru/viewtopic.php?f=7&t=78

Пишите комментарии. Подписывайтесь на рассылку, чтобы получать подобные статьи.

---

	Если Вы желаете получать уведомления о новых полезных статьях из раздела: Сантехника, водоснабжение, отопление, то оставте Ваше Имя и Email.

    Серия видеоуроков по частному дому
            Часть 1. Где бурить скважину?
            Часть 2. Обустройство скважины на воду
            Часть 3. Прокладка трубопровода от скважины до дома
            Часть 4. Автоматическое водоснабжение
    Водоснабжение
            Водоснабжение частного дома. Принцип работы. Схема подключения
            Самовсасывающие поверхностные насосы. Принцип работы. Схема подключения
            Расчет самовсасывающего насоса
            Расчет диаметров от центрального водоснабжения
            Насосная станция водоснабжения
            Как выбрать насос для скважины?
            Настройка реле давления
            Реле давления электрическая схема
            Принцип работы гидроаккумулятора
            Уклон канализации на 1 метр СНИП
    Схемы отопления
            Гидравлический расчет двухтрубной системы отопления
            Гидравлический расчет двухтрубной попутной системы отопления Петля Тихельмана
            Гидравлический расчет однотрубной системы отопления
            Гидравлический расчет лучевой разводки системы отопления
            Схема с тепловым насосом и твердотопливным котлом – логика работы
            Трехходовой клапан от valtec + термоголовка с выносным датчиком
            Почему плохо греет радиатор отопления в многоквартирном доме
            Как подключить бойлер к котлу? Варианты и схемы подключения
            Рециркуляция ГВС. Принцип работы и расчет
            Вы не правильно делаете расчет гидрострелки и коллекторов
            Ручной гидравлический расчет отопления
            Расчет теплого водяного пола и смесительных узлов
            Трехходовой клапан с сервоприводом для ГВС
            Расчеты ГВС, БКН. Находим объем, мощность змейки, время прогрева и т.п.
    Конструктор водоснабжения и отопления
            Уравнение Бернулли
            Расчет водоснабжения многоквартирных домов
    Автоматика
            Как работают сервоприводы и трехходовые клапаны
            Трехходовой клапан для перенаправления движения теплоносителя
    Отопление
            Расчет тепловой мощности радиаторов отопления
            Секция радиатора
            Зарастание и отложения в трубах ухудшают работу системы водоснабжения и отопления
            Новые насосы работают по-другому…
    Регуляторы тепла
            Комнатный термостат – принцип работы
    Смесительный узел
            Что такое смесительный узел?
            Виды смесительных узлов для отопления
    Характеристики и параметры систем
            Местные гидравлические сопротивления. Что такое КМС?
            Пропускная способность Kvs. Что это такое?
            Кипение воды под давлением – что будет?
            Что такое гистерезис в температурах и давлениях?
            Что такое инфильтрация?
            Что такое DN, Ду и PN ? Эти параметры нужно знать сантехникам и инженерам обязательно!
            Гидравлические смыслы, понятия и расчет цепей систем отопления
            Коэффициент затекания в однотрубной системе отопления
    Видео
            Отопление
                    Автоматическое управление температурой
                    Простая подпитка системы отопления
                    Теплотехника. Ограждающие конструкции.
            Теплый водяной пол
                    Насосно смесительный узел Combimix
                    Почему нужно выбрать напольное отопление?
                    Водяной теплый пол VALTEC. Видеосеминар
                    Труба для теплого пола – что выбрать?
                    Теплый водяной пол – теория, достоинства и недостатки
                    Укладка теплого водяного пола – теория и правила
                    Теплые полы в деревянном доме. Сухой теплый пол.
                    Пирог теплого водяного пола – теория и расчет
            Новость сантехникам и инженерам
            Сантехники Вы все еще занимаетесь халтурой?
            Первые итоги разработки новой программы с реалистичной трехмерной графикой
            Программа теплового расчета. Второй итог разработки
            Teplo-Raschet 3D Программа по тепловому расчету дома через ограждающие конструкции
            Итоги разработки новой программы по гидравлическому расчету
    Нормативные документы
            Нормативные требования при проектировании котельных
            Сокращенные обозначения
    Термины и определения
            Цоколь, подвал, этаж
            Котельные
    Документальное водоснабжение
            Источники водоснабжения
            Физические свойства природной воды
            Химический состав природной воды
            Бактериальное загрязнение воды
            Требования, предъявляемые к качеству воды
    Сборник вопросов
            Можно ли разместить газовую котельную в подвале жилого дома?
            Можно ли пристроить котельную к жилому дому?
            Можно ли разместить газовую котельную на крыше жилого дома?
            Как подразделяются котельные по месту их размещения?
    Личные опыты гидравлики и теплотехники
            Вступление и знакомство. Часть 1
            Гидравлическое сопротивление термостатического клапана
            Гидравлическое сопротивление колбы – фильтра
    Видеокурс
            Скачать курс Инженерно-Технические расчеты бесплатно!
    Программы для расчетов
            Technotronic8 – Программа по гидравлическим и тепловым расчетам
            Auto-Snab 3D – Гидравлический расчет в трехмерном пространстве
    Полезные материалы
    Полезная литература
            Гидростатика и гидродинамика
    Задачи по гидравлическому расчету
            Потеря напора по прямому участку трубы
            Как потери напора влияют на расход?
    Разное
            Водоснабжение частного дома своими руками
            Автономное водоснабжение
            Схема автономного водоснабжения
            Схема автоматического водоснабжения
            Схема водоснабжения частного дома
    Политика конфиденциальности

infosantehnik.ru

Температура среды — функция времени

    На рис. 4.8 изображен график функции h3 t). Сравним его с графиком переходной функции h3 t) для того же канала в теплообменнике со стенкой, имеющей нулевую теплоемкость (см. рис. 4.3). Если теплоемкость стенки равна нулю, стационарное значение выходной температуры жидкости устанавливается за конечное время, равное l/w. Действительно, если в момент времени if = 0 произошел скачок температуры среды в кожухе от нуля до единицы, то в течение времени от t — О до t = l/w из [c.141]
    Температура среды — линейная функция на конечном промежутке времени. Определим термоупругие напряжения в трех классических телах, когда те.мпература внешней омывающей, среды Тср повышается от То до Гс линейно за время т, а затем остается постоянной [см. (3.146)]. [c.383]

    Сублимация водяного пара из чистых кристаллов льда в эвтектической смеси происходит тогда, когда парциальное давление водяного пара замороженной поверхности больше, чем атмосферное давление у поверхности. Скорость сублимации кристалла льда является лишь функцией температуры. В табл. 12.3 показано, как эта скорость изменяется в диапазоне температур 173—273 К- Следует помнить, что во время лиофильной сушки образец может хорошо охладиться при сопутствующем уменьшении скорости сублимации льда из-за отвода скрытой теплоты испарения. Однако обычно достаточно теплоты за счет лучеиспускания и теплопроводности от оборудования и окружающей среды, уравновешивающих эффекты охлаждения при сублимации воды. [c.296]

    Следовательно, кинетическая функция (б). определяемая уравнением (2.51), инвариантна относительно концентрации в окружающей среде, температуры и гидродинамики процесса. Здесь оказывается безразличным, какой конкретный вид имеет функция р2(с, Г). Важно лишь то, что переменные в уравнении (2.48) разделяются. Физически это означает, что зависимость скорости растворения от концентрации и температуры не должна изменяться в процессе растворения. Наличие или отсутствие инвариантности в общем случае должно устанавливаться экспериментально в процессе определения кинетической функции. Имеющийся экспериментальный материал [3] свидетельствует о том, что инвариантность кинетической функции относительно концентрации и температуры наблюдается весьма часто, в том числе и для частиц неправильной формы. Отклонения экспериментальных данных от кривой единой кинетической функции (рис. 2.6) в области малых величин у и значениях времени, близких к полному времени растворения, становятся сравнимыми с погрешностями экспериментальных измерений. Согласно определению кинетической функции, опыты по растворению исследуемого материала естественнее всего проводить, обеспечив условие постоянства концентрации растворителя и температуры процесса. Эксперимент состоит в периодическом отборе проб растворяющегося материала и анализе его на долю нерастворившегося вещества у. В конце опыта определяется время полного растворения всей твердой фазы Хт- [c.96]

    Величина минимально определяемой концентрации натрия с помощью стеклянного электрода обусловлена переходом катионов щелочных металлов (главным образом лития) из стекла [774]. Для пяти видов серийных электродов отклонение от нернстовской функции электрода наблюдается при концентрации натрия 10,5 и использовании диэтиламина для создания щелочной среды. За счет применения аминов создается фон 0,1 мкг/л натрия. Время отклика электрода зависит от температуры при понижении температуры от 45 до 8° С время отклика увеличивается вдвое, но при этом уменьшаются помехи за счет присутствия лития. При правильном выборе условий можно определять натрий при концентрациях 0,07 мкг/л. [c.86]

    Поверхностные покрытия (краски различные типы лаков) играют двоякую роль они выполняют декоративную функцию и защищают покрываемую поверхность от вредных воздействий среды, в том числе и от микроорганизмов. Из-за постепенное отказа от введения свинца в состав красок и широкого распространения эмульсионных покрытий возникла проблема биоповреждения самих красок. Такое повреждение происходит как при хранении красок в емкостях, так и после нанесения их на поверхность и высыхания с образованием пленки. Большинство исследований в этой области направлено на создание эффективных защитных систем, которые действовали бы все то время, пока существует данное покрытие. Краски содержат пигменты, связывающие вещества, эмульгаторы, масла, смолы и смачивающие агенты они могут быть растворены в воде или в специальных растворителях. Некоторые из этих ингредиентов, например казеин, крахмал, целлюлоза и пластификаторы,, могут разрушаться микробами, а применение альтернативных, устойчивых к микробному разрушению компонентов зачастую невозможно. Развитие микроорганизмов в пленках очень сильно зависит от факторов окружающей среды температуры, влажности, наличия на поверхности питательных веществ (например, удобрений, приносимых ветром). Повреждения в емкостях часто связаны с жизнедеятельностью бактерий, но могут быть обусловлены и развитием грибов. Кроме того, в жидких эмульсионных красках могут оставаться внеклеточные ферменты, например входящие в состав целлюлазной системы эти ферменты способны снижать вязкость эмульсии. [c.241]

    Среди различных процессов с активизированным илом заслуживают внимания так называемые окислительные канавы [14]. В самой простой форме эти сооружения одновременно выполняют функции аэротенка и отстойника и эксплуатируются как перемешиваемые реакторы с регенерацией клеток. Время задержания сточных вод увеличено до 1—3 дней в зависимости от температуры. Это ведет к образованию небольшого количества ила, который в отличие от обычного активиро- [c.297]

    I] Изучать в научном смысле — значит а) не только добросовестно изображать или просто описывать, но и узнавать отношение изучаемого к тому, что известно или из опыта и сознания обычной жизненной обстановки, или из предшествующего изучения, т. е. определять и выражать качество неизвестного при помощи известного б) измерять все то, что может, подлежа измерению, показывать численное отношение изучаемого к известному, к категориям времени и пространства, к температуре, массе и т. п. в) определять место изучаемого в системе известного, пользуясь как качественными, так и количественными сведениями г) находить по измерениям эмпирическую (опытную, видимую) зависимость (функцию, закон , как говорят иногда) переменных величин, например состава от свойств, температуры от времени, свойств от массы (веса) и т. п. д) составлять гипотезы или предположения о причинной связи между изучаемым и его отношением к известному или к категориям времени, пространства и т. п. е) проверять логические следствия гипотез опытом и ж) составлять теорию изучаемого, т. е. выводить изучаемое как прямое следствие известного и тех условий, среди которых оно существует. Очевидно, что изучать что-либо возможно лишь тогда, когда нечто уже признается за исходное, несомненное, готовое в сознании. Таковым должно признать, например, число, время, пространство, вещество, форму, движение, массу. Из этого следует, что при изучении чего-либо всегда останется нечто допускаемое, как известное и признаваемое. Аксиомы геометрии могут служить тому примером. Так, в биологических науках необходимо признать способность организмов к размножению, и дух, или психику, как понятия ныне по существу пер

www.chem21.info

Расчет конечной температуры рабочих жидкостей — КиберПедия

Выше конечной целью теплового расчете являлось определение поверхности нагрева и основных размеров теплообменника для его дальнейшего конструирования. Предположим теперь, что теплообменник уже имеется или по крайней мере спроектирован. В этом случае целью теплового расчета является определение конечных температур рабочих жидкостей. Это – так называемый поверочный расчет.

При решении такой задачи известными являются следующие величины: поверхность нагрева F, коэффициент теплопередачи k, водяные эквиваленты W₁ и W₂ и начальные температуры t₁’ и t₂’, а искомыми: конечные температуры t₁” и t₂” и количество переданного тепла Q.

В приближенных расчетах можно исходить из следующих представлений. Количество тепла, отдаваемое горячей жидкостью, равно:

(2.13)

откуда конечная температура ее t₁” определяется соотношением:

(a)

Соответственно для холодной жидкости имеем:

(2.14)

и

(b)

Если принять, что температуры рабочих жидкостей меняются по линейному закону, то

(с)

Вместо неизвестных t₁” и t₂” подставим их значения из уравнений (а) и (b), тогда получим:

(d)

Произведя дальнейшее преобразование, имеем:

(e)

откуда окончательно получаем:

(2.15)

Зная количество переданного тепла Q, очень просто формулам (а) и (b) определить и конечные температуры рабочих жидкостей t₁” и t₂”.

Приведенная схема расчета, хотя и проста, однако применима лишь для ориентировочных расчетов и в случае небольших изменений температур жидкостей. В общем же случае конечная температура зависит от схемы движения рабочих жидкостей. Поэтому для прямотока и противотока ниже приводится вывод более точных формул.

1. Прямоток. Выше было показано, что температурный напор изменяется по экспоненциальному закону:

(2.16)

Имея в виду, что

и, что в конце поверхности нагрева Δt” = t₁’ – t₂’, то, подставляя эти значения в уравнение (19), последнее можно представить в следующем виде:

(2.17)

Однако, это уравнение дает лишь разности температур. Чтобы отсюда получить конечные температуры в отдельности, необходимо обе части равенства вычесть из единицы:

(2.18)

или

(2.19)

Так как

[см. разд.2.1 уравнение (2.5)].

то, подставляя это значение в левую часть уравнения (2.19), получаем:

(2.20)

Последнее уравнение, показывает, что изменение температуры горячей жидкости δt₁ равно некоторой доле П располагаемого начального температурного напора, t₁’ – t₂’; эта доля зависит только от двух безразмерных параметров и .

Аналогичным образом из уравнения (2.19) можно получить выражение и для изменения температуры холодной жидкости, а именно:

(2.21)

Определив изменения температур рабочих жидкостей и зная их начальные температуры, легко определить конечные:

(2.22)

Расход тепла определяется путем умножения водяного эквивалента жидкости на изменение ее температуры:

(2.23)

Значение функции приведено на рис. 2.5. Формулы (2.21) – (2.23) могут быть применены и для расчета промежуточных значений температуры рабочих жидкостей и количества тепла. В этом случае в, расчетные формулы вместо F надо подставить значение F_x.

Пример 2.2. Имеется водяной холодильник с поверхностью нагрева F=8 м². Определить конечные температуры жидкостей и часовое количество передаваемого тепла Q, если заданы следующие величины: V₁= 0,25 м³/час, γ₁ = 1100 кг/м³, c_p1 = 0,727 ккал/кг °С и t₁’ = 120 °С Для охлаждения в распоряжении имеется 1000 л воды в час при температуре t₂’ = 10 °С. Кроме того, известно значение коэффициента теплопередачи k = 30 ккал/м² час °С.

Соответствующее значение функции П находим из рис.2.5:

П (0,2; 1,20) = 0,64.

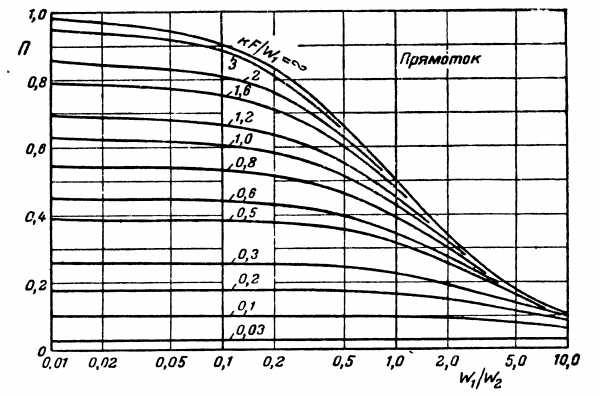
Рис. 2.5. – вспомогательная функция для расчета конечной температуры при прямотоке

 

Изменение (понижение) температуры горячей жидкости согласно уравнению (2.20) равно:

Следовательно, конечная температура ее равна:

Количество переданного тепла в час определится по уравнению (2.23)

Изменение температуры холодной жидкости определяется по уравнению (2.21). Но его можно также определить и из соотношения Q = W₂ (t₂” – t₂’), откуда

2. Противоток. Для противотока расчетные формулы выводятся так же, как и для прямотока. Окончательно они имеют следующий вид:

(2.24)

(2.25)

(2.26)

В частном случае, когда формулы

(2.24) – (2.26) принимают вид:

(2.27)

(2.28)

(2.29)

Значение функции приведено на рис. 2.6.

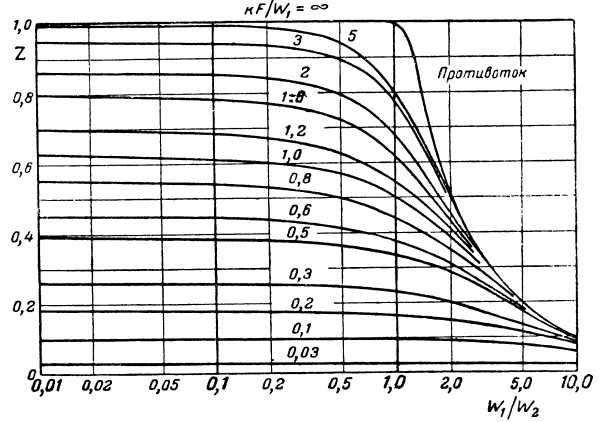
Рис. 2.6. – вспомогательная функция для расчета конечной температуры при противотоке

 

Для расчета промежуточных значений температуры рабочих жидкостей и количества переданного тепла в формулах (2.23) – (2.29) в числителе значение F заменяется на F_x, а в знаменателе остается значение полной поверхности F.

Пример 2.3. Если взять тот же теплообменник, который был рассмотрен в условиях прямотока, и допустить, что условия теплопередачи остаются без изменения (k = 30 ккал/м² час °С), то получим следующие соотношения:

Из рис. 2.6 находим значение функции Z:

Z (0,20; 1,20) = 0,68.

Изменение температуры горячей жидкости равно [уравнение (2.24)]:

Конечная температура ее:

Изменение температуры холодной жидкости [уравнение (2.25)];

Конечная температура ее:

Количество переданного тепла в час [уравнение (2.26)]:

Таким образом, в случае противотока в теплообменнике происходит более глубокое охлаждение горячей жидкости.

3. Сравнение прямотока с противотоком. Чтобы выявить преимущество одной схемы перед другой, достаточно сравнить количество передаваемого тепла при прямотоке и противотоке при равенстве прочих условий. Для этого необходимо уравнение (2.23) разделить на уравнение (2.26). В результате этого действия мы получаем новую функцию тех же двух безразмерных аргументов

характер изменения которой графически показан на рис. 2.7.

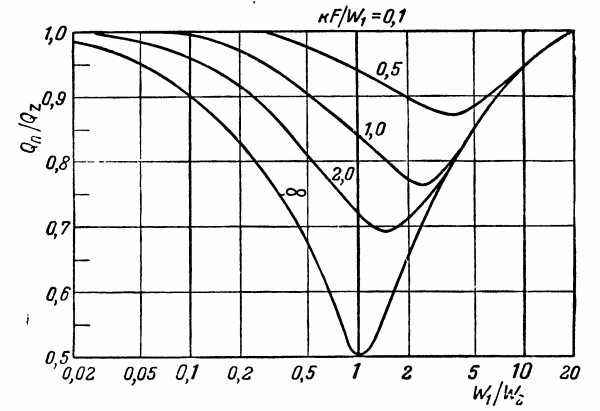
Рис. 2.7. -сравнение прямотока с противотоком

Из рисунка следует, что схемы можно считать равноценными в том случае, если водяные эквиваленты обеих жидкостей значительно отличаются один от другого (при и при ) или если значение параметра – мало. Первое условие равнозначно тому, что изменение температуры одной жидкости незначительно по сравнению с изменением температуры другой. Далее, поскольку , то второе условие соответствует случаю, когда средний температурный напор значительно превышает изменения температур рабочих жидкостей. Во всех остальных случаях при одной и той же поверхности нагрева и одинаковых крайних температурах теплоносителей при прямотоке передается меньше тепла, чем при противотоке. Поэтому с теплотехнической точки зрения всегда следует отдавать предпочтение противотоку, если какие-либо другие причины (например, конструктивные) не заставляют применять прямоток. При этом следует иметь в виду, что при противотоке создаются более тяжелые температурные условия для металла, ибо одни и те же участки стенок теплообменника с обеих сторон омываются рабочими жидкостями с наиболее высокой температурой.

При конденсации и кипении температура жидкости постоянна. Это означает, что водяной эквивалент такой жидкости бесконечно велик. В этом случае прямоток и противоток равнозначны, и уравнения (2.23) и (2.26) становятся тождественными. Конечная температура той жидкости, для которой водяной эквивалент имеет конечное значение, определяется следующим образом.

При конденсации паров;

(2.30)

и

(2.31)

При кипении жидкостей:

(2.32)

и

(2.33)

Вместо t₁ и t₂ в уравнения (2.30) – (2.33) можно подставить температуру стенки, значение которой при этом также постоянно. Значения функции находятся из таблиц показательных функций.

В случае перекрестного тока конечные температуры рабочих жидкостей находятся между конечными температурами для прямотока и противотока. Поэтому в приближенных расчетах можно пользоваться методом расчета одной из указанных схем. Если одна из жидкостей движется навстречу другой зигзагообразно (смешанный ток), то расчет может быть произведен, как для противотока.

4. Влияние тепловых потерь и проницаемости стенок.Все вышеприведенные формулы справедливы для случая, когда тепловые потери во внешнюю среду равны нулю. В действительности они всегда имеются. Более или менее точно учесть их влияние, вообще говоря, возможно, однако расчетные формулы при этом становятся громоздкими. Поэтому для учета влияния тепловых потерь в практике обычно применяется приближенный метод, который состоит в следующем.

Тепловые потери со стороны горячей жидкости вызывают более сильное падение ее .температуры. Это равносильно случаю, когда теплоотдающая жидкость в аппарате без потерь в окружающую среду имела бы меньшее значение водяного эквивалента. Поэтому влияние потерь в окружающую среду можно учесть, изменив водяной эквивалент теплоотдающей жидкости в тепловом аппарате таким образом, чтобы в последнем происходило такое же понижение температуры, как и при потоке с действительным водяным числом при наличии тепловых потерь. Внешние тепловые потери со стороны холодной жидкости оказывают обратное влияние, они уменьшают повышение температуры жидкости, что приводит к кажущемуся увеличению ее водяного эквивалента.

Наличие присоса наружного холодного воздуха оказывает такое же влияние, как и внешняя потеря тепла. Присосанный вездух на горячей стороне понижает температуру горячей жидкости (газа) точно так же, как если бы теплообменный аппарат был абсолютно непроницаем, но жидкость имела меньшее значение водяного эквивалента. Присос вездуха на холодной стороне понижает температуру холодной жидкости, что равносильно увеличению значения водяного эквивалента.

Если потеря тепла составляет р% к общему количеству передаваемого тепла, то вместо действительного значения водяного эквивалента W в расчетные формулы следует подставить значение W’ которое определяется следующим образом:

(2.34)

Знак минус (-) берется для горячей, а знак плюс (+) для холодной жидкости.

При таком способе учета внешних тепловых потерь все приведенные выше формулы для расчета конечных температур можно применять без какого-либо их изменения.

cyberpedia.su

Время охлаждения (нагрева). Расчет в Excel.

Опубликовано 14 Июл 2018
Рубрика: Теплотехника | 19 комментариев

Нестационарный режим теплообмена – это режим, когда температура тел или сред, участвующих в  процессе обмена тепловой энергией изменяется во времени. При этом время охлаждения (нагрева) – это аргумент функции температуры тела. Зависимость температуры от времени…

…характеризуется скоростью теплового обмена, которая пропорциональна разности температур тела и окружающего пространства. В отличие от стационарного режима, при котором температуры всех точек системы остаются неизменными длительное время, нестационарный теплообмен возникает, например, при помещении тела в среду с более низкой или более высокой температурой. Если среда – это условно бесконечное пространство (например, атмосферный воздух или вода в «большой» ёмкости), то влияние тела на температуру среды ничтожно, поэтому охлаждение (нагрев) тела происходит при условно постоянной температуре окружающего газа или жидкости.

Заметим, что охлаждение тела сточки зрения математики – это нагрев со знаком «минус». И нагрев, и охлаждение описываются одними и теми же формулами!

О каких задачах может идти речь? Представим небольшой перечень вопросов, на которые можно попытаться ответить, используя предложенный далее расчет в Excel:

• Сколько времени будет нагреваться деталь в печи?
• Сколько времени остывает отливка после выбивки из формы?
• Сколько времени требуется для нагрева воды в бочке на даче?
• Через какое время перемерзнет наружный водопровод при отсутствии разбора?
• Сколько времени нужно на охлаждение банки пива в холодильнике?

Расчет в Excel времени охлаждения (нагрева).

Алгоритм расчета базируется на законе Ньютона-Рихмана и на теоретических и практических исследованиях регулярного теплового режима советскими учеными Г.М. Кондратьевым («Регулярный тепловой режим», Москва, 1954г.) и М.А. Михеевым («Основы теплопередачи», Москва, 1977 г.).

Для примера выбран расчет времени нагрева до +22 °C в комнате с температурой воздуха +24 °C пивной алюминиевой банки с водой, предварительно охлажденной до +13 °C.

Исходные данные:

Параметров, необходимых для выполнения расчета времени охлаждения (нагрева) – 12 (см. скриншот).

Ориентировочные сведения о значениях коэффициента теплоотдачи α приведены в примечании к ячейке D3.

Теплофизические характеристики материала тела λ, a, ρ, c легко можно найти в справочниках или по запросу в Интернете. В нашем примере – это параметры воды.

В принципе, для выполнения расчета достаточно знать значения любой из пар характеристик:  λ, a или ρ, c. Но для возможности выполнения проверки и минимизации вероятности ошибки рекомендую заполнить значениями все 4 ячейки.

Вводим значения исходных данных в соответствующие ячейки листа Excel и считываем результат: нагрев воды от +13 °C до +22 °C в спокойном воздухе комнаты с постоянной температурой +24 °C   будет длиться 3 часа 25 минут.

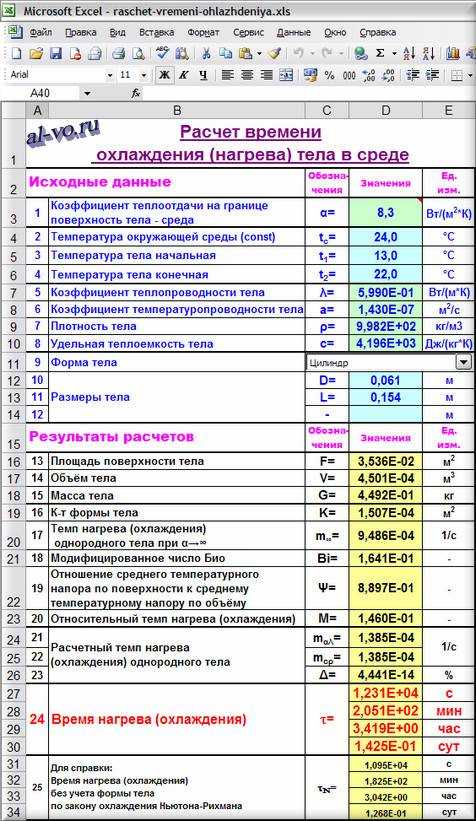
Для справки в самом конце таблицы вычислено время нагрева без учета формы тела – 3 часа 3 минуты.

Алгоритм расчета:

• 13.1. F=2·H·L+2·B·L+2·H·B – для параллелепипеда;
• 13.2. F=π·D·L+2·π·D²/4 – для цилиндра;
• 13.3. F=π·D² – для шара.
• 14.1. V=H·L·B – для параллелепипеда;
• 14.2. V=L·π·D²/4 – для цилиндра;
• 14.3. V=π·D³/6 – для шара.
• 15. G=ρ·V
• 16.1 K=((π/H)²+(π/L)²+(π/B)²)^-1 – для параллелепипеда;
• 16.2 K=((2,405/(D/2))²+(π/L)²)^-1 – для цилиндра;
• 16.3 K=((D/2)/π)² – для шара.
• 17. m_∞=a/K
• 18. Bi=α·K·F/(λ·V)
• 19. Ψ=(1+1,44·Bi+Bi²)^-0,5
• 20. M=Ψ·Bi
• 21. m_αλ=M·m_∞
• 22. m_cρ=Ψ·α·F/(c·ρ·V)
• 23. Δ=ABS (1-m_αλ/m_cρ)·100
• 24. t=(LN (ABS (t_c-t₁)) -LN (ABS (t_c-t₂))/m_αλ
• 25. t_N=(LN (ABS (t_c-t₁)) -LN (ABS (t_c-t₂)))·c·ρ·V/(α·F)

Проверка расчета опытом.

Как не трудно догадаться такой несколько странный пример выбран не случайно, а для возможности проведения простого опыта и последующего сравнения результатов. Были взяты термометр, часы и произведены замеры температуры воды в банке в процессе нагревания. Результаты расчетов и опыта отражены на графиках.

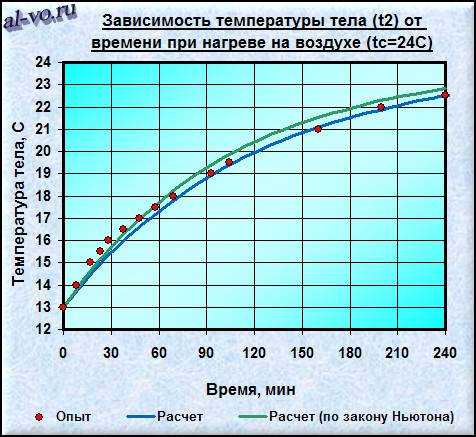
Результаты проведенного опыта показали, что нагрев банки с водой от +13 °C до +22 °C в комнате (+24 °C) продолжался примерно 3 часа 20 минут. Это на 5 минут меньше расчетного времени по Кондратьеву и на 17 минут дольше времени по классическому закону Ньютона-Рихмана.

Близость результатов и радует, и удивляет. Но не стоит переоценивать полученные итоги! Время охлаждения (нагрева), вычисленное по предложенной программе расчета в Excel, можно использовать лишь для приблизительных оценок продолжительности процессов! Дело в том, что принятые в расчете константами теплофизические характеристики тела и коэффициент теплоотдачи таковыми на самом деле не являются. Они зависят от изменяющейся температуры! К тому же регулярный режим теплообмена устанавливается не сразу после помещения тела в среду, а спустя какое-то время.

Обратите внимание, что полученные из опыта значения температур банки с водой в течение первого часа расположены выше теоретической расчетной кривой (см. графики). Это означает, что коэффициент теплоотдачи в этом периоде времени был больше выбранного нами значения α=8,3 Вт/(м²·К).

Определим среднее значение α в первые 58 минут из результатов опыта. Для этого:

• Запишем t₂=17,5 °C в ячейку D6.
• Активируем («встанем мышью») ячейку D28.
• Выполним: Сервис – Подбор параметра.
• И установим в D28 значение 58 минут, изменяя ячейку D3.

α=9,2 Вт/(м²·К)!!!

Проделав ту же процедуру для t₂=22,5 °C и t=240 мин, получим α=8,3 Вт/(м²·К).

Выбранное при теоретическом расчете значение α (по рекомендации СП 50.13330.2012 и формуле из Справочника по физике – см. примечание к ячейке D3) чудесным образом, хотя и совершенно случайно, совпало со значением α, вычисленным по опытным данным.

Рассмотренным способом можно определять реальные точные средние значения коэффициента теплоотдачи тел с любой формой поверхности по практическим замерам всего двух значений температуры тела и промежутка времени между этими замерами.

Остается добавить, что температура банки с водой после рассмотренных 4-х часов в последующее время будет асимптотически приближаться к 24 °C.

Прошу уважающих труд автора  скачивать файл с программой расчетов после подписки на анонсы статей!

Ссылка на скачивание файла: vremya-ohlazhdeniya (xls 55,5KB).

P.S.

Так сколько часов составит время охлаждения алюминиевой банки с пивом 0,45 л от +20 °C до +8 °C в  холодильнике (+3°C)? По расчету в программе – 2,2…2,4 часа. Опытом не проверял… 🙂

P.P.S.

Любопытный (возможно, только для меня) факт обнаружился при работе над статьей. И у куба с размером ребер a, и у цилиндра с диаметром а и длиной а, и у шара с диаметром а отношение объема к площади поверхности одинаковое: V/F=a/6!!!

Другие статьи автора блога

На главную

Статьи с близкой тематикой

Отзывы

al-vo.ru

Плотность воды как функция температуры

    Подставляя в формулу (10) приведенные выше значения вязкости нефти (14) и плотности воды и нефти (12) и (11), выраженные как функции температуры, получаем общее выражение, характеризующее зависимость скорости оседания в нефти капли пресной воды от температуры [c.43]

    Плотность жидкостей обычно исследуют как функцию температуры и давления. Метод гидростатического взвешивания. В случае жидкостей этот метод несколько отличается от применяемого для исследования плотности твердых тел. Плотность исследуемой жидкости определяют по выталкивающей силе, действующей на твердое тело, погруженное в нее. Объем погружаемого в жидкость твердого тела определяют путем взвешивания его в воздухе и воде, после чего [c.435]

    Конечно, в действительности плотность воды при низких температурах является сложной, нелинейной функцией температуры. Во многих рассматриваемых случаях широкий диапазон изменения параметров i, 5 и р не позволяет считать постоянными коэффициенты р и р и пренебрегать зависимостью плотности от температуры. В табл. 12.4.5 приведены значения коэффициента р для морской воды с концентрацией соли 0,35 % и для пресной воды при р = 0,1 МПа и изменении температуры в небольшом, но типичном для практики диапазоне. [c.189]

    Плотность и удельный объем жидкости. Плотность жидких смесей фреонов 11 и 12 выше плотности воды и, так же как плотность паров, является функцией температуры. Жидкий фреон-11 плотнее фреона-12, поэтому плотность смесей тем больше, чем выше содержание фреона-11 (табл.8.10). [c.147]

    Предполагается, что при плавлении льда в основном сохраняется описанный выше ближний порядок. Но, поскольку ближний порядок не идеальный, характерный для льда дальний порядок нарушается. При повышении температуры число ближайших соседей возрастает, т. е. плотная упаковка становится более вероятной. Однако в то же время расстояние между соседними молекулами увеличивается. Поэтому не удивительно, что плотность не является монотонной функцией температуры. Между О и 4° доминирующим фактором является увеличение координационного числа, а выше 4° — увеличение расстояния между ядрами. При достаточно высоких температурах структура воды с водородными связями полностью разрушается, и вода ведет себя как обычная жидкость. [c.114]

    На рис. 9.3 приведена графическая зависимость отрицательного логарифма ионного произведения воды рК от температуры на линии равновесия жидкой воды с ее паром. Следует учесть, что функция не является чисто температурной, а в какой-то степени и плотностной, т.е. изменение происходит в результате изменения не только температуры, но и плотности воды. [c.119]

    Влияние же температуры на плотность воды имеет существенно большее значение. Запишем функцию  [c.81]

    Очевидно, что это сделать нельзя. В самом деле, какие физические измерения осуществимы над данной термодинамической системой (рекой) Можно измерять температуру воды, ее плотность, вязкость, молярный объем, электропроводность, изотопное отношение 0/ 0, температуры плавления и кипения, химическую чистоту и множество других свойств. Все эти свойства являются функциями состояния. Температура воды зависит только от ее сиюминутного состояния и не зависит от ее предыстории. (Конечно, температура может зависеть от того, что происходило в прошлом, но для измерения температуры совершенно нет необходимости знать предысторию системы.) Изменение температуры воды между городами А и Б можно установить, измеряя температуру воды в реке в этих двух городах  [c.17]

    Если мы установим, что изменение температуры воды в городах Д и Б одинаково в нерабочий и любой другой день, то можно утверждать, что всякое количество теплоты, поступающее в воду в реакторе, должно быть точно скомпенсировано работой, выполненной водой в турбинах (или охлаждением воды перед ее сбрасыванием в реку). И наоборот, каждая порция работы, полученная в турбинах, должна быть скомпенсирована теплотой, полученной в реакторе, иначе вода в городе Б окажется холоднее, чем в городе А. Никакие сведения о воде в этих двух городах не позволяют сделать вывода о количестве теплоты (q), поступившем в воду, или о работе (w), проделанной водой. Ни теплота, ни работа не являются функциями состояния, но их разность является функцией состояния. Если величина — W не поддерживается постоянной, это можно обнаружить, измеряя те или иные свойства воды в городе Б. Наиболее очевидным из таких свойств является температура, но изменению подвергнутся и другие свойства, например молярный объем, плотность, электропроводность и пр. И наоборот, если мы установим состояние воды в городах А и Б, то это значит, что мы установим изменение величины q — w в результате протекания воды по территории государства справа, хотя мы в отдельности не измеряли значения величин q и w. Их разность представляет собой изменение функции состояния, Е. [c.18]

    Титан имеет довольно высокую (1668 °С) температуру плавления и плотность 4,5 г/см . Благодаря высокой удельной прочности и превосходным противокоррозионным свойствам его широко применяют в авиационной технике. В настоящее время его используют также для изготовления оборудования химических производств. В ряду напряжений титан является активным металлом расчетный стандартный потенциал для реакции Т + + 2ё Л составляет —1,63 В . В активном состоянии он может окисляться с переходом в раствор в виде ионов Т ” [1]. Металл легко пассивируется в аэрированных водных растворах, включая разбавленные кислоты и щелочи. В пассивном состоянии титан покрыт нестехиометрической оксидной пленкой усредненный состав пленки соответствует ТЮ . Полупроводниковые свойства пассивирующей пленки обусловлены в основном наличием кислородных анионных вакансий и междоузельных ионов Т , которые выполняют функцию доноров электронов и обеспечивают оксиду проводимость /г-типа. Потенциал титана в морской воде близок к потенциалу нержавеющих сталей. Фладе-потенциал имеет довольно отрицательное значение (Ер = —0,05В) [2, 3], что указывает на устойчивую пассивность металла. Нарушение пассивности происходит только под действием крепких кислот и щелочей и сопровождается значительной коррозией. [c.372]

    Здесь а — поверхностное натяжение жидкости, г — скрытая теплота испарения, — коэффициенты динамической и кинематической вязкости. Чем больше число тем эффективнее теплоноситель. Поскольку параметры, входящие в N , по-разному зависят от температуры, то функция N (7) имеет минимум, отвечающий наивыгоднейшему температурному диапазону работы термосифона. Однако эта величина не полностью характеризует теплоноситель и лишь отражает его свойства в жидком состоянии. По этому числу предпочтение следует отдать дистиллированной воде (ее скрытая теплота испарения велика 2400 кДж/кг). Однако при минусовых температурах вода замерза

www.chem21.info

изменение температуры как функции времени



изменение температуры как функции времени

Mathematics: the change in temperature as a function of time

Универсальный русско-английский словарь. Академик.ру. 2011.

• изменение температуры жидкости
• изменение температуры масла

Смотреть что такое “изменение температуры как функции времени” в других словарях:

• Как солить, перчить, приправлять —         Когда продукт будь то мясо, рыба или овощи прошел все операции от разделки до тепловой обработки и когда блюдо уже почти готово, то, даже если все проделано правильно, оно еще не имеет законченного вкуса, ему еще чего то не хватает. Это… …   Большая энциклопедия кулинарного искусства

• Часы прибор для измерения времени — Содержание: 1) Исторический очерк развития часовых механизмов: а) солнечные Ч., b) водяные Ч., с) песочные Ч., d) колесные Ч. 2) Общие сведения. 3) Описание астрономических Ч. 4.) Маятник, его компенсация. 5) Конструкции спусков Ч. 6) Хронометры …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

• ГОСТ Р МЭК 60880-2010: Атомные электростанции. Системы контроля и управления, важные для безопасности. Программное обеспечение компьютерных систем, выполняющих функции категории А — Терминология ГОСТ Р МЭК 60880 2010: Атомные электростанции. Системы контроля и управления, важные для безопасности. Программное обеспечение компьютерных систем, выполняющих функции категории А оригинал документа: 3.25 N версионное программное… …   Словарь-справочник терминов нормативно-технической документации

• ХИМИЯ ПОВЕРХНОСТНЫХ ЯВЛЕНИЙ — изучает химические силы, действующие на поверхности. В общем случае химия поверхности рассматривает свойства трех состояний вещества твердого (Т), жидкого (Ж) и газообразного (Г) и дает описание вещества как фазовой системы. Однако если два… …   Энциклопедия Кольера

• СТО 70238424.27.140.042-2009: Гидроэлектростанции. Долговременные наблюдения за развитием техноприродных процессов в зоне взаимодействия оснований и сооружений. Нормы и требования — Терминология СТО 70238424.27.140.042 2009: Гидроэлектростанции. Долговременные наблюдения за развитием техноприродных процессов в зоне взаимодействия оснований и сооружений. Нормы и требования: 3.1 безнапорная фильтрация : Фильтрация жидкости в… …   Словарь-справочник терминов нормативно-технической документации

• время — 3.3.4 время tE (time tE): время нагрева начальным пусковым переменным током IА обмотки ротора или статора от температуры, достигаемой в номинальном режиме работы, до допустимой температуры при максимальной температуре окружающей среды. Источник …   Словарь-справочник терминов нормативно-технической документации

• Фьючерс — (Futures) Фьючерс это срочный биржевой контракт на покупку рыночного актива Что такое фьючерс, фьючерсный контракт, рынок фьючерсов, торговля фьючерсами, стратегия фьючерс, виды ценных бумаг на фьючерсном рынке, хеджирование рисков с помощью… …   Энциклопедия инвестора

• Инфляция — (Inflation) Инфляция это обесценивание денежной единицы, уменьшение ее покупательной способности Общая информация об инфляции, виды инфляции, в чем состоит экономическая сущность, причины и последствия инфляции, показатели и индекс инфляции, как… …   Энциклопедия инвестора

• Статистическая физика —         раздел физики, задача которого выразить свойства макроскопических тел, т. е. систем, состоящих из очень большого числа одинаковых частиц (молекул, атомов, электронов и т.д.), через свойства этих частиц и взаимодействие между ними.… …   Большая советская энциклопедия

• Кинетика физическая —         теория неравновесных макроскопических процессов, то есть процессов, возникающих в системах, выведенных из состояния теплового (термодинамического) равновесия. К К. ф. можно отнести термодинамику неравновесных процессов (См. Термодинамика… …   Большая советская энциклопедия

• Планк, Макс — Эта статья  о немецком физике. Другие значения термина в заглавии статьи см. на Планк (значения). Макс Планк Max Planck …   Википедия

universal_ru_en.academic.ru