Изохорная и изобарная теплоемкости воздуха. Пример задачи
Изохорная и изобарная теплоемкости воздуха. Пример задачи
От DA
24.01.2019 22:31Термодинамика газов является специальным разделом физики, который изучает и исследует поведение газовых систем при различных внешних условиях. В данной статье рассмотрим вопрос теплоемкости воздуха с использованием модели идеального газа.
Воздух – идеальный газ
Прежде чем раскрывать вопрос теплоемкости воздуха, рассмотрим модель идеального газа. В соответствии с ней полагают, что система состоит из невзаимодействующих друг с другом частиц, которые хаотично движутся в ограниченном объеме пространства. Скорости частиц подчиняются классическому распределению Максвелла-Больцмана. Модель также предполагает, что частицы являются безразмерными.
Насколько точно в приведенную модель вписывается воздушная смесь? Известно, что воздух состоит в основном из молекул азота и кислорода. Эти молекулы являются химически нейтральными. Существующие между ними ван-дер-ваальсовые взаимодействия являются очень слабыми, поэтому их при выполнении термодинамических расчетов можно не учитывать. Что касается размеров молекул, то ими также можно пренебречь, так как расстояния между ними на несколько порядков больше. Таким образом, воздух очень хорошо описывается моделью идеального газа.
Теплоемкость и ее виды
Согласно физическому определению, теплоемкость – это величина, показывающая, сколько нужно на систему затратить теплоты, чтобы ее нагреть на 1 градус Цельсия или на 1 кельвин. Поскольку процессы нагревания и охлаждения являются обратимыми, то при охлаждении системы на 1 градус выделяется количество теплоты, равное ее теплоемкости.
Как физическая величина теплоемкость может быть абсолютной, молярной или массовой. Определение абсолютной теплоемкости для произвольной системы было дано выше. Молярной называется теплоемкость на 1 моль газа, массовой – на 1 кг газа. Молярная величина чаще используется для рассматриваемого агрегатного состояния материи.
В зависимости от изопроцесса, при котором измеряют теплоемкость, она бывает изохорной и изобарной. В первом случае в системе с газом не изменяется объем, во втором случае сохраняется давление.
Формулы изохорной и изобарной теплоемкостей воздуха
Сначала рассмотрим изохорную величину. Обозначим ее CV. Первое начало термодинамики, которое следует из закона сохранения энергии, для изохорного процесса выглядит следующим образом:
H = dU
То есть все тепло H, подводимое к системе, идет на увеличение ее внутренней энергии. Изменение величины U можно записать так:
dU = CV*dT
С другой стороны, если воспользоваться универсальным уравнением состояния идеальной газовой системы, то формула для dU запишется в виде:
dU = z/2*n*R*dT
Здесь z – количество степеней свободы молекул, n – количество вещества, R – постоянная, dT – изменение температуры. Выражение выше следует из того факта, что внутренняя энергия идеального газа в точности равна кинетической энергии его молекул.
Из сравнения двух равенств получаем формулу для изохорной теплоемкости:
CV = z/2*n*R
В случае воздуха z=5, поскольку он на 99 % состоит из двухатомных молекул азота и кислорода (двухатомные молекулы имеют 3 поступательные и 2 вращательные степени свободы). Полагая n=1 моль, приходим к формуле изохорной молярной теплоемкости воздуха:
CV = 5/2*R = 2,5*R
Напомним, что постоянная R равна 8,314, тогда CV = 20,785 Дж/(моль*К).
Теперь определим молярную изобарную теплоемкость воздуха. Поскольку в результате изобарного нагрева газ расширяется, то он выполняет некоторую работу. Первое начало термодинамики в этом случае принимает вид:
H = dU + P*dV
Энтальпия H через изобарную теплоемкость CP для 1 моль вещества запишется так:
H = CP*dT
Работу газа с использованием уравнения Клапейрона-Менделеева можно записать так:
P*dV = R*dT
Эти выражения позволяют записать следующее соотношение изобарной и изохорной теплоемкостей:
CP = CV + R
Подставляя величину CV для воздуха, получаем изобарную молярную теплоемкость для него:
CP = 2,5*R + R = 3,5*R = 29,099 Дж/(моль*К)
Таким образом, величина CP оказывается больше, чем CV.
Пример решения задачи
В цилиндре под поршнем находятся 3 моль воздуха при атмосферном давлении. В процессе нагрева цилиндра поршень стал подниматься, сохраняя постоянное давление в системе. Чему равна работа газа при расширении, если известно, что его конечная температура стала больше начальной на 10 oC?
Воспользуемся первым законом термодинамики для изобарного нагрева:
n*CP*dT = n*CV*dT + P*dV
Отсюда работа газа (третье слагаемое) выразится так:
P*dV = n*(CP – CV)*dT
Подставляя данные из условия задачи, а также значения молярных теплоемкостей воздуха, получаем ответ: воздух в цилиндре, расширяясь, совершит работу 249,42 Дж.
www.navolne.life
Изохорная и изобарная теплоемкости воздуха. Пример задачи :: SYL.ru
Термодинамика газов является специальным разделом физики, который изучает и исследует поведение газовых систем при различных внешних условиях. В данной статье рассмотрим вопрос теплоемкости воздуха с использованием модели идеального газа.
Воздух – идеальный газ
Прежде чем раскрывать вопрос теплоемкости воздуха, рассмотрим модель идеального газа. В соответствии с ней полагают, что система состоит из невзаимодействующих друг с другом частиц, которые хаотично движутся в ограниченном объеме пространства. Скорости частиц подчиняются классическому распределению Максвелла-Больцмана. Модель также предполагает, что частицы являются безразмерными.
Насколько точно в приведенную модель вписывается воздушная смесь? Известно, что воздух состоит в основном из молекул азота и кислорода. Эти молекулы являются химически нейтральными. Существующие между ними ван-дер-ваальсовые взаимодействия являются очень слабыми, поэтому их при выполнении термодинамических расчетов можно не учитывать. Что касается размеров молекул, то ими также можно пренебречь, так как расстояния между ними на несколько порядков больше. Таким образом, воздух очень хорошо описывается моделью идеального газа.
Теплоемкость и ее виды
Согласно физическому определению, теплоемкость – это величина, показывающая, сколько нужно на систему затратить теплоты, чтобы ее нагреть на 1 градус Цельсия или на 1 кельвин. Поскольку процессы нагревания и охлаждения являются обратимыми, то при охлаждении системы на 1 градус выделяется количество теплоты, равное ее теплоемкости.
Как физическая величина теплоемкость может быть абсолютной, молярной или массовой. Определение абсолютной теплоемкости для произвольной системы было дано выше. Молярной называется теплоемкость на 1 моль газа, массовой – на 1 кг газа. Молярная величина чаще используется для рассматриваемого агрегатного состояния материи.
В зависимости от изопроцесса, при котором измеряют теплоемкость, она бывает изохорной и изобарной. В первом случае в системе с газом не изменяется объем, во втором случае сохраняется давление.
Формулы изохорной и изобарной теплоемкостей воздуха
Сначала рассмотрим изохорную величину. Обозначим ее CV. Первое начало термодинамики, которое следует из закона сохранения энергии, для изохорного процесса выглядит следующим образом:
H = dU
То есть все тепло H, подводимое к системе, идет на увеличение ее внутренней энергии. Изменение величины U можно записать так:
dU = CV*dT
С другой стороны, если воспользоваться универсальным уравнением состояния идеальной газовой системы, то формула для dU запишется в виде:
dU = z/2*n*R*dT
Здесь z – количество степеней свободы молекул, n – количество вещества, R – постоянная, dT – изменение температуры. Выражение выше следует из того факта, что внутренняя энергия идеального газа в точности равна кинетической энергии его молекул.
Из сравнения двух равенств получаем формулу для изохорной теплоемкости:
CV = z/2*n*R
В случае воздуха z=5, поскольку он на 99 % состоит из двухатомных молекул азота и кислорода (двухатомные молекулы имеют 3 поступательные и 2 вращательные степени свободы). Полагая n=1 моль, приходим к формуле изохорной молярной теплоемкости воздуха:
CV = 5/2*R = 2,5*R
Напомним, что постоянная R равна 8,314, тогда CV = 20,785 Дж/(моль*К).
Теперь определим молярную изобарную теплоемкость воздуха. Поскольку в результате изобарного нагрева газ расширяется, то он выполняет некоторую работу. Первое начало термодинамики в этом случае принимает вид:
H = dU + P*dV
Энтальпия H через изобарную теплоемкость CP для 1 моль вещества запишется так:
H = CP*dT
Работу газа с использованием уравнения Клапейрона-Менделеева можно записать так:
P*dV = R*dT
Эти выражения позволяют записать следующее соотношение изобарной и изохорной теплоемкостей:
CP = CV + R
Подставляя величину CV для воздуха, получаем изобарную молярную теплоемкость для него:
CP = 2,5*R + R = 3,5*R = 29,099 Дж/(моль*К)
Таким образом, величина CP оказывается больше, чем CV.
Пример решения задачи
В цилиндре под поршнем находятся 3 моль воздуха при атмосферном давлении. В процессе нагрева цилиндра поршень стал подниматься, сохраняя постоянное давление в системе. Чему равна работа газа при расширении, если известно, что его конечная температура стала больше начальной на 10 oC?
Воспользуемся первым законом термодинамики для изобарного нагрева:
n*CP*dT = n*CV*dT + P*dV
Отсюда работа газа (третье слагаемое) выразится так:
P*dV = n*(CP – CV)*dT
Подставляя данные из условия задачи, а также значения молярных теплоемкостей воздуха, получаем ответ: воздух в цилиндре, расширяясь, совершит работу 249,42 Дж.
www.syl.ru
| Золото | 129 |
| Свинец | 130 |
| Иридий | 134 |
| Вольфрам | 134 |
| Платина | 134 |
| Ртуть | 139 |
| Олово | 218 |
| Серебро | 234 |
| Цинк | 380 |
| Латунь | 380 |
| Медь | 385 |
| Константан | 410 |
| Железо | 444 |
| Сталь | 460 |
| Высоколегированная сталь | 480 |
| Чугун | 500 |
| Никель | 500 |
| Алмаз | 502 |
| Флинт (стекло) | 503 |
| Кронглас (стекло) | 670 |
| Кварцевое стекло | 703 |
| Сера ромбическая | 710 |
| Кварц | 750 |
| Гранит | 770 |
| Фарфор | 800 |
| Цемент | 800 |
| Кальцит | 800 |
| Базальт | 820 |
| Песок | 835 |
| Графит | 840 |
| Кирпич | 840 |
| Оконное стекло | 840 |
| Асбест | 840 |
| Кокс (0…100 °С) | 840 |
| Известь | 840 |
| Волокно минеральное | 840 |
| Земля (сухая) | 840 |
| Мрамор | 840 |
| Соль поваренная | 880 |
| Слюда | 880 |
| Нефть | 880 |
| Глина | 900 |
| Соль каменная | 920 |
| Асфальт | 920 |
| Кислород | 920 |
| Алюминий | 930 |
| Трихлорэтилен | 930 |
| Абсоцемент | 960 |
| Силикатный кирпич | 1000 |
| Полихлорвинил | 1000 |
| Хлороформ | 1000 |
| Воздух (сухой) | 1005 |
| Азот | 1042 |
| Гипс | 1090 |
| Бетон | 1130 |
| Сахар-песок | 1250 |
| Хлопок | 1300 |
| Каменный уголь | 1300 |
| Бумага (сухая) | 1340 |
| Серная кислота (100%) | 1340 |
| Сухой лед (твердый CO2) | 1380 |
| Полистирол | 1380 |
| Полиуретан | 1380 |
| Резина (твердая) | 1420 |
| Бензол | 1420 |
| Текстолит | 1470 |
| Солидол | 1470 |
| Целлюлоза | 1500 |
| Кожа | 1510 |
| Бакелит | 1590 |
| Шерсть | 1700 |
| Машинное масло | 1670 |
| Пробка | 1680 |
| Толуол | 1720 |
| Винилпласт | 1760 |
| Скипидар | 1800 |
| Бериллий | 1824 |
| Керосин бытовой | 1880 |
| Пластмасса | 1900 |
| Соляная кислота (17%) | 1930 |
| Земля (влажная) | 2000 |
| Вода (пар при 100 °C) | 2020 |
| Бензин | 2050 |
| Вода (лед при 0 °C) | 2060 |
| Сгущенное молоко | 2061 |
| Деготь каменноугольный | 2090 |
| Ацетон | 2160 |
| Сало | 2175 |
| Парафин | 2200 |
| Древесноволокнистая плита | 2300 |
| Этиленгликоль | 2300 |
| Этанол (спирт) | 2390 |
| Дерево (дуб) | 2400 |
| Глицерин | 2430 |
| Метиловый спирт | 2470 |
| Говядина жирная | 2510 |
| Патока | 2650 |
| Масло сливочное | 2680 |
| Дерево (пихта) | 2700 |
| Свинина, баранина | 2845 |
| Печень | 3010 |
| Азотная кислота (100%) | 3100 |
| Яичный белок (куриный) | 3140 |
| Сыр | 3140 |
| Говядина постная | 3220 |
| Мясо птицы | 3300 |
| Картофель | 3430 |
| Тело человека | 3470 |
| Сметана | 3550 |
| Литий | 3582 |
| Яблоки | 3600 |
| Колбаса | 3600 |
| Рыба постная | 3600 |
| Апельсины, лимоны | 3670 |
| Сусло пивное | 3927 |
| Вода морская (6% соли) | 3780 |
| Грибы | 3900 |
| Вода морская (3% соли) | 3930 |
| Вода морская (0,5% соли) | 4100 |
| Вода | 4183 |
| Нашатырный спирт | 4730 |
| Столярный клей | 4190 |
| Гелий | 5190 |
| Водород | 14300 |
energy.clcnet.ru
Теплоемкость изобарная – Энциклопедия по машиностроению XXL
При известном значении истинной массовой теплоемкости изобарного процесса теплота рабочему телу (или отводимая), определяется уравнением (109). [c.135]Для обратимого изобарного процесса при постоянной теплоемкости измене 1ие энтропии находится по уравнению (6-40) [c.92]
Из определения политропного процесса следует, что основные термодинамические процессы — изохорный, изобарный, изотермический и адиабатный, если они протекают при постоянной теплоемкости, являются частными случаями политропного процесса.
При температуре 7 , давлении Р , компонентном составе С, и любом произвольно взятом массовом расходе Р из уравнений (4,1.1)-(4.1.44) рассчитываются при E ,ц = 1 параметры исходного газа удельная энтальпия 1 д, удельная изобарная Ср и удельная изохорная теплоемкости, показатель адиабаты к , газовая постоянная Р д, плотность р . [c.169]
Так как для одноатомного идеального газа теплоемкости Су и Ср не зависят от температуры и являются постоянными, то для него (и только для него) изохорный и изобарный процессы являются поли-тропными. [c.45]
Так как для излучения изобарный процесс одновременно является изотермическим, то p = j = o, поскольку изотермическая теплоемкость равна бесконечности. Это следует также из соотношения [c.360]
Изохорный и изобарный процессы представляются ъ Т — s-диа-грамме кривыми, как это видно из уравнений (7,5) и (7.6). При постоянных значениях теплоемкостей построение дает логарифмические кривые при значениях 6 == / (Т) эти кривые несколько изменяют свой вид. [c.84]
Рассмотрим неизотермическое течение газа около плоской поверхности с достаточно малыми числами Маха и постоянными значениями изобарной теплоемкости Ср, динамической вязкости ц и теплопроводности X. Дифференциальные [c.27]
Теплоемкость тела зависит от условий нагревания. Наиболее употребительны теплоемкость при постоянном давлении (изобарная теплоемкость) Ср, теплоемкость при постоянном объеме (изохорная теплоемкость) и теплоемкость под давлением насыщенных паров (вдоль линии сосуществования фаз) s. Величины Ср и v, Дж/ (моль-К), связаны соотношением [c.197]
Разность изобарной и изохорной молярных теплоемкостей Ср—Дж/(моль-К), разреженных газов описывается соотношением Ср—с = к, где R — универсальная газовая постоянная.
| Таблица 9. 1. Молярная изобарная теплоемкость Ср элементов при температуре 298,15 К и давление 0,10135 МПа | 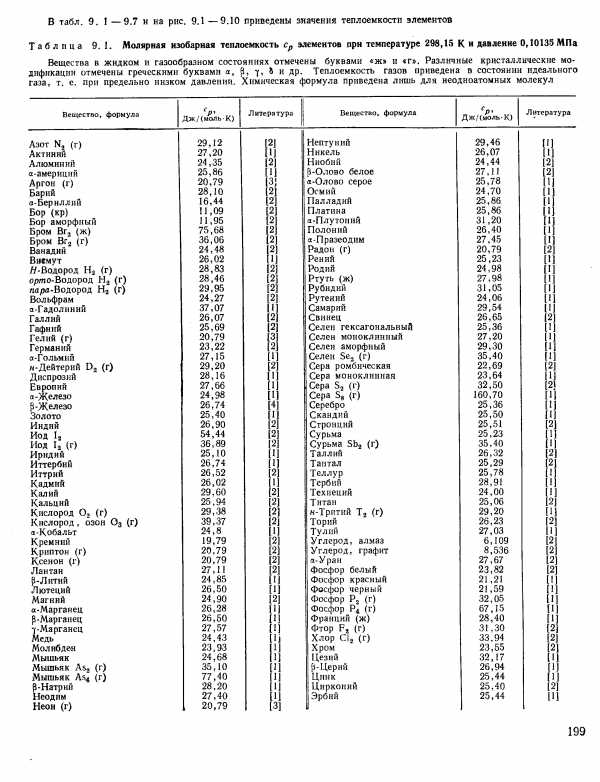 |
| Таблица 9.2. Удельная изобарная теплоемкость Ср, Дж/(кг К), элементов при температуре от 20 до | 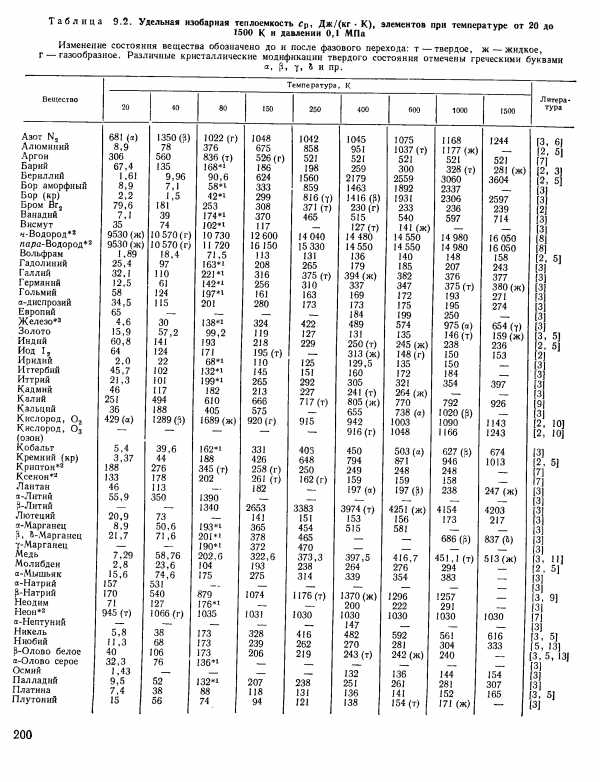 |
| Таблица 9.5. Зависимость удельной изобарной теплоемкости Ср, кДж/(кг К), элементов в жидком и газообразном состояниях от давления и температуры | 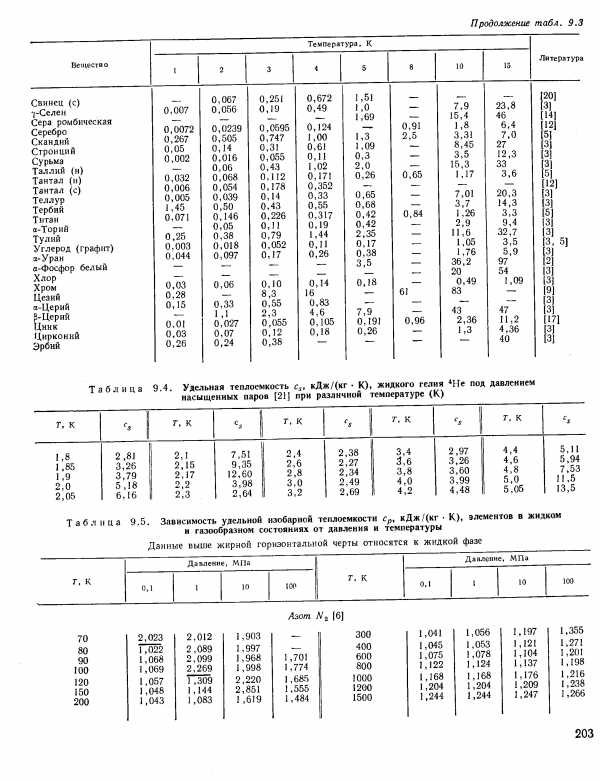 |
| Рис. 9.9. Молярная изобарная теплоемкость жидкой серы [4] | 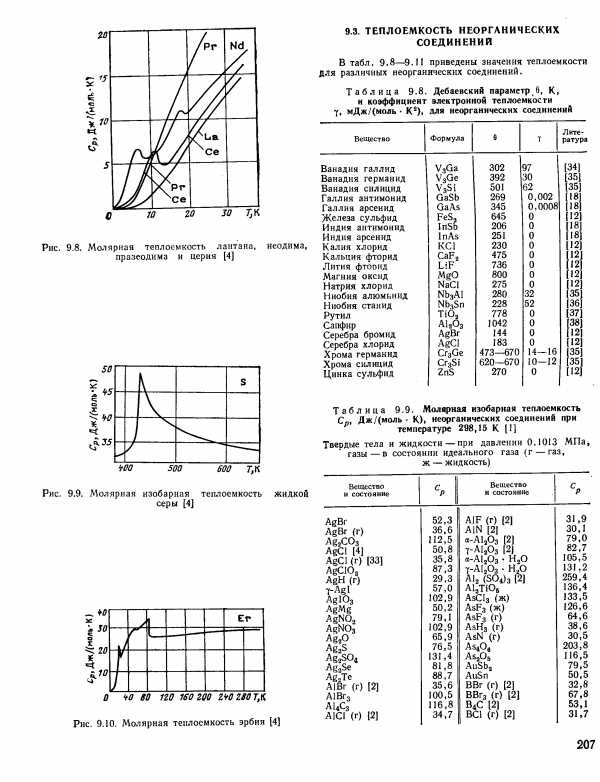 |
| Таблица 9.10. Молярная изобарная теплоемкость Ср, Дж/(моль К), неорганических соединений при температуре от 20 до 1500 К и давлении 0,1013 МПа [2, 4] | 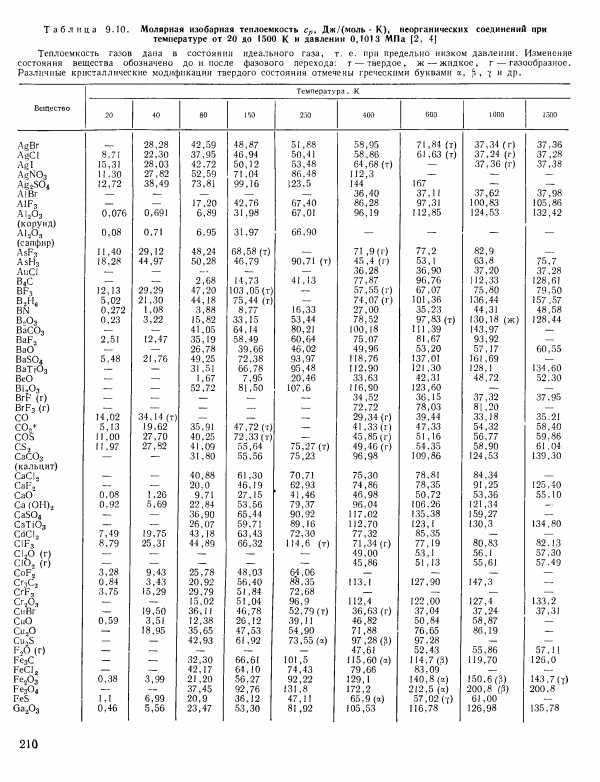 |
| Таблица 9. П. Зависимость удельной изобарной теплоемкости Ср, кДж/(кг К), аммиака, воды, водяного пара и углекислого газа от давления и температуры | 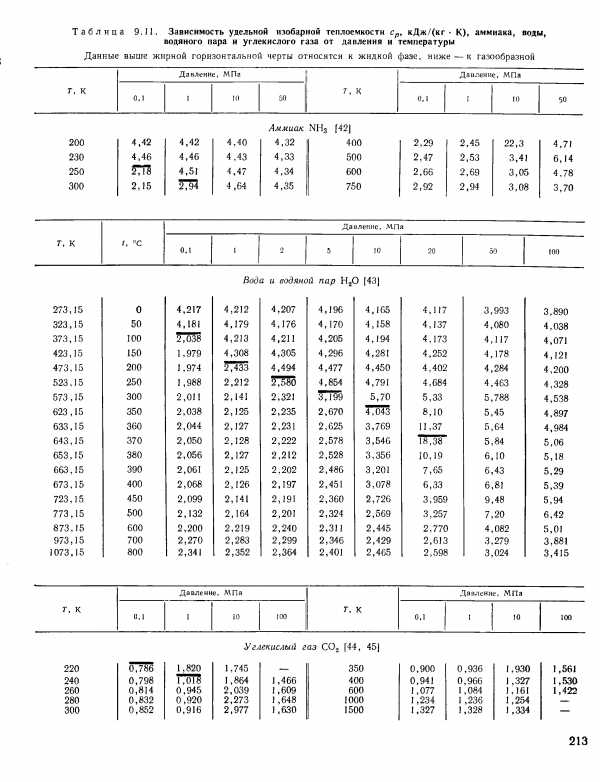 |
| Таблица 9.14. Зависимость удельной изобарной теплоемкости Ср, кДж/(кг К), органических жидкостей | 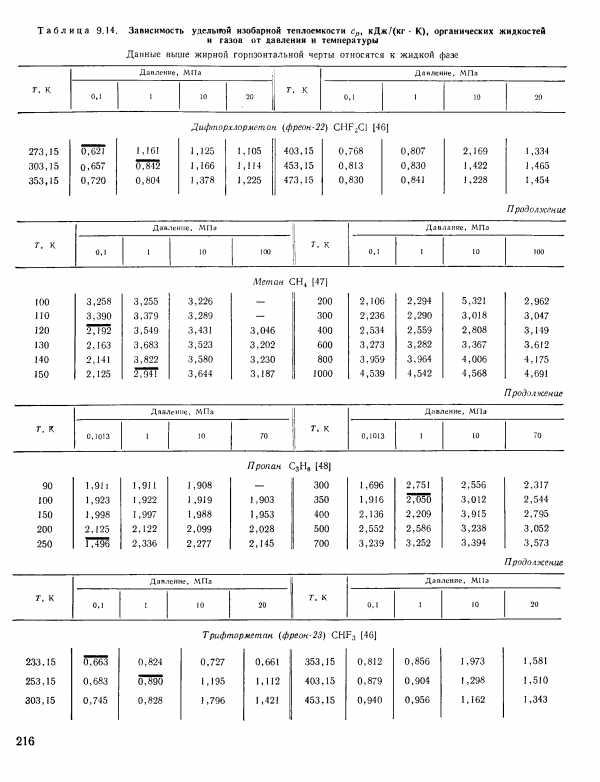 |
Наиболее часто на практике используются теплоемкости изобарного (2=р = 1дет) и изохорного (2=0 = бет) процессов теплоемкости называются изобарной и изохорной и обозначаются соответственно Ср и Сщ. [c.27]
Согласно квантовой теории теплоемкости изобарная теплоемкость идеа.пьного газа зависит только от температуры, и поэтому в любом термодинамическом процессе идеального газа изменение энтальпии может быть найдено из формулы [c.18]
Наиболее часто на практике используются теплоемкости изобарного (a =/)= onst) и изохорного (a =y= onst) процессов эти теплоемкости называются изобарной и изохорной теплоемкостями. Они обозначаются соответственно и [c.24]
Теплоемкость газов изменяется в процессе сгорания вместе с изменением температуры и состава рабочей смеси. В тепловых расчетах удобнее всего использовать средние мольные теплоемкости — изобарную Ср (при р == onst) и изохорную Сг, (при V — onst) разность между ними, как известно, есть величина постоянная, равная для одного моля [c.53]
При значении п = 0 получаем р = onst, т. е. уравнение изобары. Теплоемкость изобарного процесса [c.106]
Теплоемкость и энтальпия вла 1Кного воздуха. Изобарную теплоемкость влажного воздуха Ср обычно относят к 1 кг сухого воздуха, т. е. к (1 – -d) кг влажного воздуха. Она равна сумме теплоемкостей 1 кг сухого воздуха и с/ кг пара [c.42]
В приближенных термодинамических расчетах процессов с влажным воздухом в небольшом диапазоне температур можно применять удельную изобарную теплоемкость сухого воздуха Срв= 1 кДж/(кг-К) = onst, удельную изобарную теплоемкость водяного пара Срв 2 кДж/(кг К) = onsl. В этом случае, выражая теплоемкость в кДж/(кг-К), получаем [c.42]
Количество теплоты, сообн1,епное телу в изобарном процессе при постоянной теплоемкости, равно [c.92]
Дифференциальные уравнения, связывающие теплоемкость при постоянном давлетт и теплоемкость при постоянном объеме, имеют большое значение в термодинамике. Как уже отмечалось, обычно С , определяется из эксперимента, а из уравнений, связывающих С , и Су, можно определить и С[-. Уравнение (10-27) применительно к изобарному процессу при р onst, когда dQ dT ,, запишется так [c.161]
Часто внутренее тепловыделение отсутствует и на установившемся режиме теплосъем будет определяться лишь величиной необратимых потерь за счет неадиабатности камеры холода и магистралей подвода и отвода охлажденного газа Q = Q . По известному значению потребной холодопроизводительности и выбранному значению изобарного подогрева охлажденных масс газа, считая изобарную теплоемкость известной, по уравнению теплового баланса определяют потребный расход охлажценного потока [c.228]
Поток газа из первой ячейки вынужденного вихря через сечение 0-0 имеет параметры массовый расход С ], компонентный состав удельную энтальпию Сваь удельные изобарную Ср и изохорную теплоемкости, показатель адиабаты газовую постоянную плотность рсннь статическую температуру T , [c.165]
После того, как все ячейки вихревого течения, начиная от первой, будут просчитаны, г.е. л – т = 0, то определяются расход газовой фазы вынужденного вихря – (6.63), температура охлажденного газа – (6.64), удельная изобарная теплоемкость охлажденного газа Ср – (6.65), компонентный состав охлажденного газа iJ – (6.66), удельная холодопроизводительноеть удельная теплоемкость С, при давлении Р и температуре Г, – (4.1.37), (4.1.36), (4.1.34), (4.1.35), эффективность энергоразделения т – (6.70), а также температура газа 7 , истекшего из свободного вихря при давлении Р – (6.67). [c.170]
После эзого находится максимальное давление 7,п, – (7.1), максимальная температура T yj – (7.2), удельная изобарная теплоемкость (4.1.25), (4.1.26), (4.1.34)- [c.182]
При минимальной температуре и давления Р газа за слоем столкновения в полузамкнутой емкости из системы уравнений (4.1.34) – (4.1.37) находится удельная изобарная теплоемкость Сртш газа. [c.255]
В изобарном процессе p= onst dp — О, а. удельная теплоемкость равна [c.44]
Согласно закону распределения каждая поступательная и вращательная степень свободы молекулы дает в молярную изохорную теплоемкость вклад, равный R/2, а каждая возбужденная колебательная — вклад, равный R. Колебательные степени свободы возбуждаются и дают вклад в теплоемкость лишь при высокой температуре T>hvlk, где V — частота колебаний атомов в молекуле). При учете поступательных и вращательных степеней свободы и пренебрежении колебательными закон равнораспределения дает для молярных изохорной v и изобарной Ср теплоемкостей, Дж/(моль-К) Сц=1,5 R Ср = 2,5 R — для одноатомного газа tr = 2,5/ Ср = 3,5/ — для двухатомного газа v=3 / Ср = 4 Л — для многоатомного газа. [c.197]
mash-xxl.info
Определение теплоёмкости воздуха. Освоение методики калориметрического эксперимента на примере определения изобарной теплоёмкости воздуха, страница 2
Пусть при бесконечно малом изменении состояния тела количество теплоты dQ вызывает изменение температуры тела dT, тогда теплоёмкость тела в данном процессе выразится отношением:
или
Единицей теплоёмкости является Дж/К.
Теплоёмкость С зависит от внешних условий или характера процесса, при котором происходит отвод или подвод теплоты. Так, например, теплоёмкость газов в случае подвода теплоты при постоянном объеме отличается от удельной теплоёмкости газов при постоянном давлении .
Удельная теплоёмкость есть отношение теплоёмкости к массе вещества.
.
Если С выражается в Дж/К, m – в кг, то с – в Дж/(кг·К).
Объёмная теплоёмкость [Дж/(м·К)]
, где и – плотность и объём газа при нормальных физических условиях, кг/м; м.
Молярная теплоёмкость [Дж/(м·К)]
, где n – количество рабочего вещества, моль.
3. Формула Майера.
4. Формула для определения количества тепла при постоянной и переменной теплоёмкостях.
Пользуясь истинной удельной теплоёмкостью, требуёмое количество теплоты для нагрева m вещества от температуры до ºС определим из выражения:
где – требуемое количество теплоты.
Здесь интеграл берётся по пути процесса от 1 до 2 (от начального состояния до заданного конечного), так как изменение температуры тела зависит от характера процесса, а с этим связанно изменение теплоёмкости тела . Удельное количество теплоты является, таким образом, функцией процесса и не является поэтому функцией состояния системы, изменения которой зависит только от начального и конечного состояний.
Теплоёмкость газа не постоянна. Для идеального газа она является функцией температуры. Теплоёмкость зависит от температуры, а также от давления и объёма. При низких давлениях и высоких температурах теплоёмкость газа считают приближенно зависящей от температуры.
В общем случае истинная теплоёмкость для температуры t с достаточной степенью точности выражается для большинства газов уравнением второй степени (нелинейным)
, где a, b, e – постоянные, определяемые для различных газов и видов теплоёмкости на основании экспериментальных и теоретических данных.
Количество теплоты в изохорном термодинамическом процессе:
и
а при
где – удельная теплоёмкость тела при постоянном объёме.
Количество теплоты изобарном термодинамическом процессе:
и
а при
где – удельная теплоёмкость тела при постоянном давлении.
Количество теплоты в изотермическом термодинамическом процессе:
.
5. Физический смысл внутренней энергии и энтальпии газа. Формулы для их вычисления.
Внутреннюю энергию рассматривают с молекулярной точки зрения как сумму кинетической и потенциальной энергий, обусловленных хаотическим движением и взаимодействием молекул газа. Другие виды энергии не учитываются, так как при рассматриваемых в технической термодинамике температурах их влиянием на изменение состояния можно пренебречь.
Для реальных газов внутренняя энергия является функцией как температуры , так и плотности газа :
.
Внутреннюю энергию можно найти из первого закона термодинамики:
,
Для изохорного процесса.
Для изобарного .
Для изотермического
Для адиабатного .
Параметром состояния газа наряду с внутренней энергией является удельная энтропия:
она определяется исключительно функциями состояния ().
Энтальпия имеет особо важное значение для техники в случае непрерывного потока рабочего тела. С ее помощью значительно упрощаются рассмотрения процессов и их расчеты.
Величина i выражается в Дж/кг, если слагаемые u и pv – в Дж/кг.
Энтальпия представляет энергию, связанную с данным состоянием тела, т. е. является функцией состояния, поскольку u и pv – функции состояния.
В процессе с постоянным давлением :
т.е. изменение удельной энтальпии равно количеству теплоты, подведенной к телу при .
Из выражения находим:
или
Энтальпия – экстенсивная (аддитивная) величина. Удельная энтальпия обладает интенсивными свойствами.
Удельную теплоёмкость при постоянном давлении можно определить следующим образом:
но
Сравнивая последние два выражения, видим, что при постоянном давлении удельная энтальпия обладает свойствами, аналогичные тем, которые имеет внутренняя энергия при постоянном объёме.
Из определения удельной энтальпии:
Поскольку внутренняя энергия является лишь функцией температуры, то также зависит только от температуры. Отсюда для идеального газа:
а при находим:
и для любого изменения от состояния 1 до состояния 2
6. Сущность калориметрического метода определения теплоёмкости газа.
Опытное определение изобарной теплоемкости газа сводиться к нагреву его в проточном калориметре и измерению необходимых величин (количества тепла , объёмного расхода и повышения температуры ). Полагая, что все тепло от электронагревателя идёт в установившемся процессе на изобарный нагрев воздуха (тепловые потери отсутствуют), теплоёмкость можно найти по формуле, :
Вывод
Я изучил первый закон термодинамики и все виды теплоёмкостей газов. Освоил методику калориметрического эксперимента на примере определения изобарной объёмной теплоёмкости воздуха, которая равна , величина расхождения между экспериментально определенной теплоёмкостью и табличным значением равна %, это обусловлено погрешностью измерений и нагрева воздуха от электронасоса.
vunivere.ru
Определение изобарной теплоемкости воздуха (Лабораторная работа № 8)
Министерство образования РФ
ГОУВПО «КнАГТУ»
Кафедра «Судовые энергетические установки»
Лабораторная работа №8
Определение изобарной теплоемкости воздуха
Преподаватель: Звиняцкий А.Я.
Группа: 0ХБ-1
Студент: Никифоров В.В.
Комсомольск-на-Амуре
2004
Цель работы: освоить методику экспериментального определения удельной массовой изобарной теплоемкости воздуха.
Принципиальная схема экспериментальной установки
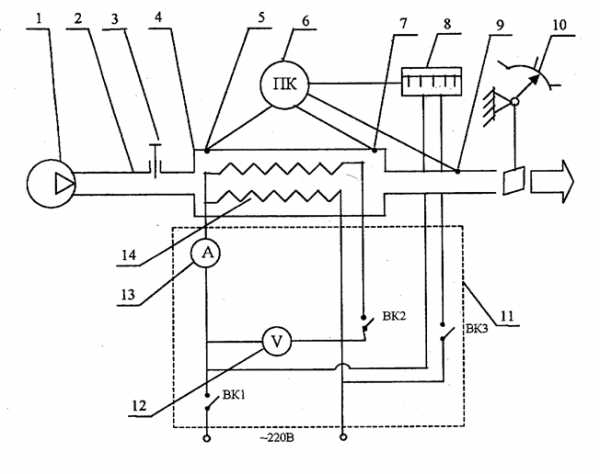
1) – вентилятор;
2) – воздухопровод;
3) – заслонка;
4) – калорифер;
5,7,9) – термопары;
6) – переключатель термопар;
8) – потенциометр;
10) – лопаточный расходомер;
11) – щит контроля и управления;
12) – вольтметр;
13) – амперметр;
14) – нагреватель.
Протокол проведенных опытов
Номер опыта | Расход воздуха Vt, м3/с | Температура калорифера | Параметры нагревателя | Температура на выходе t3, °C | Теплоемкость Ср, Дж/(кг*К) | ||
на входе t1, °C | на выходе t2, °C | I, A | V, B | ||||
1 | 0,370 | 22,0 | 35,5 | 30 | 231 | 26,0 | 1057 |
2 | 0,455 | 21,5 | 31,5 | 25,5 | 1161 | ||
3 | 0,490 | 21,5 | 31,0 | 25,5 | 1136 | ||
4 | 0,550 | 21,5 | 30,0 | 26,0 | 1131 | ||
Обработка результатов опытов
1) Определить количество теплоты Q, Дж/с, подведенной к воздуху в калорифере за единицу времени, по выражению:
2) По барометру лаборатории измерить барометрическое давление и найти плотность воздуха в условиях опыта по выражению:
3) Определить массу воздуха m, кг/с, прокачиваемого через калорифер в единицу времени:
4) По замеренным и вычисленным величинам найти среднюю удельную массовую изобарную теплоемкость воздуха по выражению:
5) Определим относительную погрешность:
Вывод: В ходе данной лабораторной работы мы, изменяя расход пропускаемого воздуха, замеряли температуру воздуха на входе и выходе и расчитывали изобарную теплоемкость. Относительная погрешность экспериментальной теплоемкости составила 11%.
vunivere.ru
Плотность, теплопроводность, теплоемкость кислорода O2
Плотность, теплоемкость, свойства кислорода O2
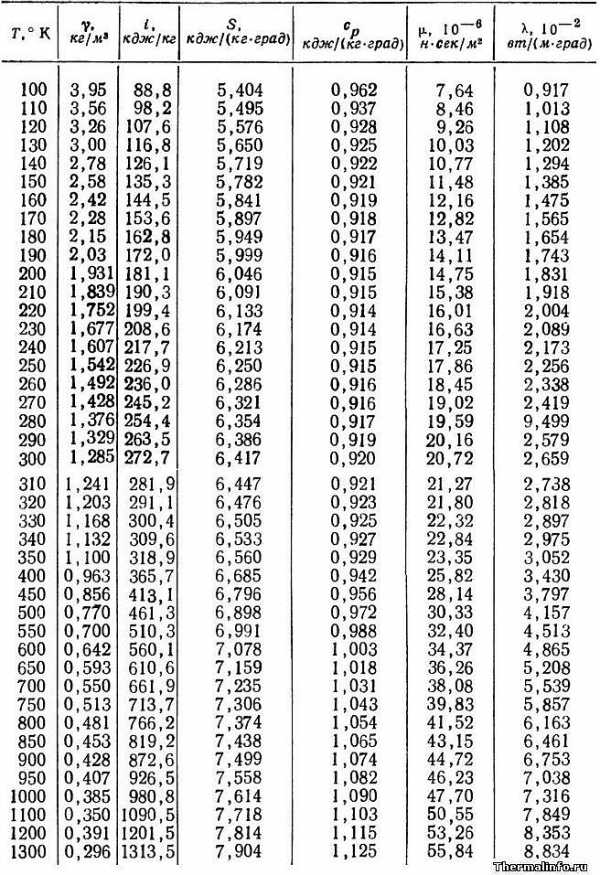
В таблице представлены теплофизические свойства кислорода такие, как плотность, энтальпия, энтропия, удельная теплоемкость, динамическая вязкость, коэффициент теплопроводности. Свойства в таблице даны для газообразного кислорода, находящегося при атмосферном давлении, в зависимости от температуры в интервале от 100 до 1300 К.
Плотность кислорода равна 1,329 кг/м3при комнатной температуре. При нагревании кислорода, его плотность уменьшается. Теплопроводность кислорода равна 0,0258 Вт/(м·град) при комнатной температуре и при повышении температуры этого газа увеличивается.
Удельная теплоемкость кислорода при комнатной температуре равна 919 Дж/(кг·град). Теплоемкость кислорода увеличивается при росте его температуры. Также при нагревании кислорода увеличиваются значения таких его свойств, как энтальпия, энтропия и вязкость.
Примечание: будьте внимательны! Теплопроводность в таблице указана в степени 102. Не забудьте разделить на 100.
Теплопроводность кислорода в жидком и газообразном состояниях
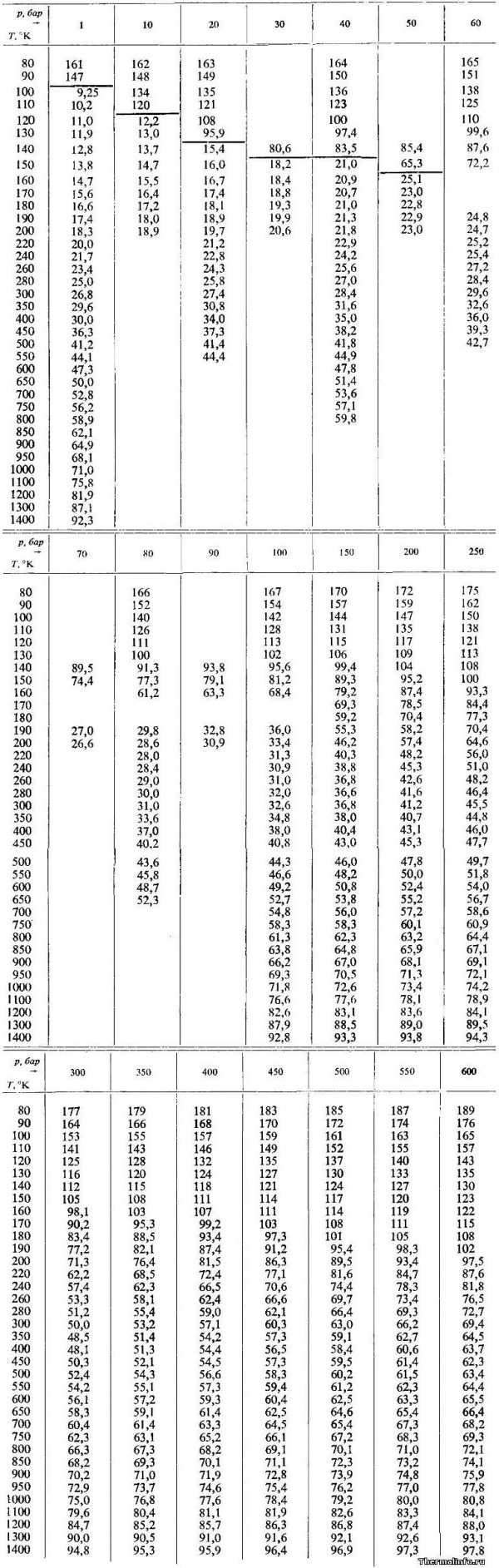
В таблице приведены значения коэффициента теплопроводности кислорода в жидком и газообразном состояниях при различных температурах и давлениях. Теплопроводность указана в интервале температуры от 80 до 1400 К и давления от 1 до 600 атм.
Значения теплопроводности в таблице, находящиеся выше черты, относятся к жидкому кислороду, а ниже ее — к газообразному. По данным таблицы видно, что теплопроводность жидкого кислорода выше, чем газообразного и при росте давления увеличивается.
Примечание: Будьте внимательны! Теплопроводность в таблице дана в степени 103. Не забудьте разделить на 1000. Размерность Вт/(м·град).
Теплопроводность кислорода при высоких температурах
В таблице даны значения коэффициента теплопроводности кислорода при высоких температурах (от 1600 до 6000 К) и давлении от 0,001 до 100 атм.
При температурах выше 1300°С кислород начинает диссоциировать, и при некотором давлении его теплопроводность достигает максимальных значений. По данным таблицы видно, что теплопроводность диссоциированного кислорода при высоких температурах может достигать величин до 3,73 Вт/(м·град).
Примечание: Будьте внимательны! Теплопроводность в таблице дана в степени 103. Не забудьте разделить на 1000.

Теплопроводность жидкого кислорода на линии насыщения
В таблице указаны значения коэффициента теплопроводности жидкого кислорода на линии насыщения. Теплопроводность дана в диапазоне температуры от 90 до 150 К. Следует отметить, что теплопроводность жидкого кислорода при увеличении температуры снижается.
Примечание: Будьте внимательны! Теплопроводность в таблице дана в степени 103. Не забудьте разделить на 1000.
Источники:
1. Варгафтик Н.Б. Справочник по теплофизическим свойствам газов и жидкостей.
2. Чиркин В.С. Теплофизические свойства материалов ядерной техники.
thermalinfo.ru