Теплоемкость воздуха
Теплоемкость как физическая величина показывает количество тепловой энергии, которое необходимо для изменения температуры рабочего тела, в данном случае, воздуха, на один градус. Теплоемкость воздуха непосредственно зависит от температуры и давления. При этом для исследования разных видов теплоемкости могут применяться различные методы.
Математически теплоемкость воздуха выражается как отношение количества тепла к приращению его температуры. Теплоемкость тела, имеющего массу 1 кг, принято называть удельной. Молярная теплоемкость воздуха – теплоемкость одного моля вещества. Обозначается теплоемкость – Дж/К. Молярная теплоемкость соответственно Дж/(моль*К).
Теплоемкость можно считать физической характеристикой какого-либо вещества, в данном случае воздуха, в том случае, если измерение проводится в постоянных условиях. Чаще всего подобные измерения проводятся при постоянном давлении. Так определяется изобарная теплоемкость воздуха. Она возрастает с увеличение температуры и давления, а также является линейной функцией данных величин. В этом случае изменение температуры происходит при постоянном давлении. Для расчета изобарной теплоемкости необходимо определить псевдокритическую температуру и давление. Она определяется с использованием справочных данных.
Теплоемкость воздуха. Особенности
Воздух представляет собой газовую смесь. При их рассмотрении в термодинамике приняты следующие допущения. Каждый газ в составе смеси должен быть равномерно распределен по всему объемы. Таким образом, объем газа равен объему всей смеси. Каждый газ в составе смеси обладает своим парциальным давлением, которое он оказывает на стенки сосуда. Каждый из компонентов газовой смеси должен иметь температуру, равную температуре всей смеси. При этом сумма парциальных давлений всех компонентов равняется давлению смеси. Расчет теплоемкости воздуха выполняется на основе данных о составе газовой смеси и теплоемкости отдельных компонентов.
Теплоемкость неоднозначно характеризует вещество. Из первого закона термодинамики можно сделать вывод, что внутренняя энергия тела изменяется не только в зависимости от количества полученного тепла, но и от совершенной телом работы. При различных условиях протекания процесса теплопередачи, работа тела может различаться. Таким образом, одинаковое сообщенное телу количество теплоты, может вызвать различные по значению изменения температуры и внутренней энергии тела. Эта особенность характерна только для газообразных веществ. В отличие от твердых и жидких тел, газообразные вещества, могут сильно изменять объем и совершать работу. Именно поэтому теплоемкость воздуха определяет характер самого термодинамического процесса.
Однако при постоянном объеме воздух не совершает работу. Поэтому изменение внутренней энергии пропорционально изменению его температуры. Отношение теплоемкости в процессе с постоянным давлением, к теплоемкости в процессе с постоянным объемом является частью формулы адиабатного процесса. Оно обозначается греческой литерой гамма.
Из истории
Термины «теплоемкость» и «количество теплоты» не очень удачно описывают свою суть. Связано это с тем, что они пришли в современную науку из теории теплорода, которая была популярна в восемнадцатом веке. Последователи этой теории рассматривали теплоту как некое невесомое вещество, которое содержится в телах. Это вещество не может быть ни уничтожено, ни создано. Охлаждение и нагревание тел объясняли уменьшением или увеличением содержания теплорода соответственно. Со временем эта теория была признана несостоятельной. Она не могла объяснить, почему одинаковое изменение внутренней энергии какого-либо тела получается при передаче ему разного количества теплоты, а также зависит от совершаемой телом работы.
fb.ru
Молярная теплоемкость газов – Справочник химика 21
Зависимость молярной теплоемкости газов от температуры может быть выражена в виде простого уравнения [c.456]
Средняя молярная теплоемкость газов при различной температуре и постоянном объеме Со 155] [c.55]
Таким образом, становится ясным, что из данных о молярной теплоемкости газов можно сделать некоторые выводы о строении молекул. В гл. 3 мы познакомимся с важными кванто-вом( ханическими уточнениями этих представлений. [c.22]
Средняя молярная теплоемкость газов от О до I С при нормальном, давлении [55] [c.54]
Уравнение (225) представляет собой закон Кирхгофа в интегральной форме. Очевидно, что температурная зависимость энтальпии для газовых реакций, в уравнении реакции которых по обе стороны знака равенства находятся одинаковые молярные количества газов, очень невелика, так как молярная теплоемкость газов почти не зависит от природы газа. В то же время для реакций, в которых образуется или расходуется газообразное вещество, можно ожидать существенную зависимость энтальпии от температуры.
Дж/моль-град. Так как молярные теплоемкости газов равны, эта величина в точности компенсирует недостачу колебательной составляющей теплоемкости NO2. Таким образом, разность колебательных составляющих теплоемкостей NjO и NO2 составляет [c.93]
Примечание. Расчет табл. 30 произведен для средних условий ([c.477]
Для определения теплоемкости при высоких или повышенных давлениях можно использовать график, приведенный на рис. 37, который позволяет определить разность между молярной теплоемкостью при требуемом давлении Ср и молярной теплоемкостью газа при нормальных условиях с” в зависимости от приведенной температуры. [c.104]
Уравнения температурной вависимости средней молярной теплоемкости газов от О до 1 °С при нормальном давлении [c.55]
Быстрым сжатием воздуха, в котором находится какое-нибудь горючее вещество, можно вызвать его воспламенение. Это явление положено в основу действия двигателя внутреннего сгорания Дизеля. Воспламенение при сжатии возможно вследствие того, что коэффициент Джоуля—Томсона для воздуха положителен, а также поскольку при сжатии газа над ним выполняется работа (см. гл. 17). Чтобы определить, какое давление необходимо создать для воспламенения горючей смеси, нужно знать молярную теплоемкость газа С (количество калорий, требующееся для повы-щения температуры одного моля газа на один градус Цельсия), а также количество работы, выполненной над газом, и, наконец, температуру самовозгорания горючего. Для воздуха С равно около 5 кал моль -град Если сжать воздух до 1/30 первоначального объема, который он занимав I при комнатной температуре (293 К), то приближенно можно определить его температуру после сжатия, пользуясь соотно-щением [c.162]
Если нагревать газ при постоянном объеме, то работа внешних сил будет равна нулю и все подведенное извне тепло пойдет на увеличение его внутренней энергии. Таким образом, молярная теплоемкость газа при постоянном объеме с численно равна изменению внутренней энергии одного моля газа при повышении его температуры на 1 град. [c.100]
Анализ уравнения (8) показывает, что составляющая работы А зависит от указанных выще факторов Н, Кщ, 0 , у о в той же мере, как и составляющая Особенность этой составляющей заключается в том, что она в меньщей степени, чем величина Асж зависит от длины колонки и скорости газа-носителя, но в значительной мере определяется разностью температур колонки Г к и окружающей среды То, а также молярной теплоемкостью газа-носителя Ср. . [c.53]
Молярные теплоемкости газов. В одноатомных газах (Не и др.) атомы движутся только поступательно по трем координатным осям и молярная теплоемкость таких газов [c.185]
МОЛЯРНАЯ ТЕПЛОЕМКОСТЬ ГАЗОВ И ГАЗОВЫХ СМЕСЕЙ ПРИ ВЫСОКИХ ДАВЛЕНИЯХ [c.749]
Для молярной теплоемкости газа от 298 до 1000°К предложены НО] эмпирические уравнения [c.415]
На основе теоретических соображений о распределении энергии молекул газа между различными видами движения — поступательным, вращательным и колебательным — можно рассчитать молярную теплоемкость газа, значения которой приведены во втором столбце табл. 1. [c.73]
Средние молярные теплоемкости газов в интервале 0—800° составляют (в кал град)-. [c.44]
Молярную теплоемкость газов молосновании кинетической теории, поскольку, как было по
www.chem21.info
Теплоемкость (удельная, молярная). Уравнение Майера.
Теплоемкость тела показывает, какое количество теплоты необходимо для увеличения температуры тела на 1 градус. Зависит от материала вещества и от массы тела.
Удельная теплоемкость показывает, какое количество теплоты необходимо для нагревания 1 килограмма вещества на 1 градус.
Молярная теплоемкость показывает, какое количество теплоты необходимо для нагрева 1 моля вещества на 1 градус.
Удельная и молярные теплоемкости идеального газа зависят не только от химического состава газа, но и от процесса, с помощью которого происходит изменение температуры.
Изохорный процесс – при постоянном объеме, значит, работа не совершается. Для одноатомного идеального газа
Удельная теплоемкость в этом процессе
Молярная теплоемкость
2.Изобарный процесс – процесс при постоянном давлении.
Удельная теплоемкость для изобарного процесса
Молярная теплоемкость для изобарного процесса
3.Изотермический процесс – это процесс при постоянной температуре.
так как
4.Адиабатный процесс – это процесс при отсутствии теплопередачи с системой.
Для реализации такого процесса необходимо изолировать систему от окружающей среды, или процесс должен проходить быстро, не успевая приходить в тепловое равновесие с окружающей средой.
Первый закон термодинамики для адиабатного процесса:
При адиабатном расширении температура понижается.
При адиабатном сжатии температура газа повышается.
Уравнение Майера.
Найдем связь между Ср и Сv идеального газа. Используя формулы запишем первое начало термодинамики в виде
или
Ср = Сv + R. (3.16)
Формулу (3.16) называют уравнением Майера.
Вывод: при изобарическом нагревании газа к нему подводится больше теплоты, чем при изохорическом.
Практически изобарический процесс можно осуществить, например, при нагревании или охлаждении газа в цилиндре с подвижным поршнем, на который действует постоянная сила давления.
Работу при изобарическом расширении идеального газа можно найти по формуле
(3.17)
или
(3.18)
Если при изменении температуры Ср не изменяется, то теплоту, сообщенную газу в изобарическом процессе, можно найти по формуле
(3.19)
P-V диаграмма изобарического процесса приведена на рис. 3.4, где площадь прямоугольника (заштрихованная часть рисунка) численно равна работе газа в этом процессе.
Циклические процессы. Цикл Карно. КПД цикла Карно.
Цикл Карно
Цикл Карно совершает газ, находящийся в цилиндре под поршнем. На изотермическом участке (1–2) газ приводится в тепловой контакт с горячим тепловым резервуаром (нагревателем), имеющим температуру T1. Газ изотермически расширяется, совершая работу A12, при этом к газу подводится некоторое количество теплоты Q1 = A12. Далее на адиабатическом участке (2–3) газ помещается в адиабатическую оболочку и продолжает расширяться в отсутствие теплообмена. На этом участке газ совершает работу A23 > 0. Температура газа при адиабатическом расширении падает до значения T2. На следующем изотермическом участке (3–4) газ приводится в тепловой контакт с холодным тепловым резервуаром (холодильником) при температуре T2 < T1. Происходит процесс изотермического сжатия. Газ совершает работу A34 < 0 и отдает тепло Q2 < 0, равное произведенной работе A34. Внутренняя энергия газа не изменяется. Наконец, на последнем участке адиабатического сжатия газ вновь помещается в адиабатическую оболочку. При сжатии температура газа повышается до значения T1, газ совершает работу A41 < 0. Полная работа A, совершаемая газом за цикл, равна сумме работ на отдельных участках:
A = A12 + A23 + A34 + A41
На диаграмме (p, V) эта работа равна площади цикла. Процессы на всех участках цикла Карно предполагаются квазистатическими. В частности, оба изотермических участка (1–2 и 3–4) проводятся при бесконечно малой разности температур между рабочим телом (газом) и тепловым резервуаром (нагревателем или холодильником).Как следует из первого закона термодинамики, работа газа при адиабатическом расширении (или сжатии) равна убыли ΔU его внутренней энергии. Для одного моля газа
A = –ΔU = –CV (T2 – T1),
где T1 и T2 – начальная и конечная температуры газа.
Отсюда следует, что работы, совершенные газом на двух адиабатических участках цикла Карно, одинаковы по модулю и противоположны по знакам
A23 = –A41
По определению, коэффициент полезного действия η цикла Карно есть
1.1. КПД цикла
С. Карно выразил коэффициент полезного действия цикла через температуры нагревателя T1 и холодильника T2:
Цикл Карно замечателен тем, что на всех его участках отсутствует соприкосновение тел с различными температурами. Любое состояние рабочего тела (газа) на цикле является квазиравновесным, т. е. бесконечно близким к состоянию теплового равновесия с при конечной разности температур рабочего тела и окружающей среды (термостатов), когда тепло может передаваться без совершения работы. Поэтому цикл Карно – наиболее эффективный круговой процесс из всех возможных при заданных температурах нагревателя и холодильника:
ηКарно = ηmax
infopedia.su
ОПРЕДЕЛЕНИЕ ТЕПЛОЕМКОСТИ ВОЗДУХА
⇐ ПредыдущаяСтр 5 из 6Следующая ⇒
Цель работы: познакомиться с процессом изобарического нагревания воздуха, определить молярную теплоемкость воздуха при изобарическом нагревании.
Оборудование: нагреватель, компрессор, термопара с мультиметром, блок питания, амперметр и вольтметр.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Теплоемкость – это теплофизический параметр веществ, определяемый как количество теплоты, необходимое для нагревания некоторой массы вещества на один Кельвин. Если масса вещества равна одному килограмму, то теплоемкость называется удельной теплоемкостью, если масса равна одному моль, то – молярной теплоемкостью. По определению молярная теплоемкость равна
. (1)
Здесь ν = – количество вещества в моль, m – масса, M – масса одного моль, dQ – количество теплоты, достаточной для повышения температуры на dT. Для газов, в отличие от твердых и жидких тел, теплоемкость зависит от вида происходящего с газом термодинамического процесса нагревания. Это связано с тем, что, согласно первому началу термодинамики
, (2)
теплота расходуется не только на повышение внутренней энергии dU, то есть на повышение температуры, но и на работу изменения объема газа. В отличие от твердых и жидких тел изменение объема может быть сравнительно большим и зависит от вида термодинамического процесса. Поэтому величина работы сил давления и количество теплоты, необходимое для нагревания газа, также зависит от вида процесса.
Рассмотрим нагревание идеального газа. Идеальный газ – это газ, собственный объем молекул которого ничтожно мал по сравнению с объемом сосуда, и потенциальная энергия взаимодействия молекул отсутствует. Воздух при нормальных условиях можно считать идеальным газом.
Приизохорическом нагревании газа изменения объема нет, работы нет, и теплота идет только на повышение внутренней энергии, dQ = dU. Для идеального газа, согласно молекулярно-кинетической теории, внутренняя энергия – это кинетическая энергия молекул . Откуда молярная теплоемкость при изохорическом нагревании идеального газа равна .
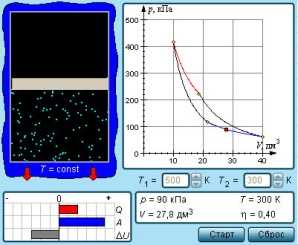
Приизобарическом нагревании газа в условиях постоянного давления дополнительно часть теплоты расходуется на работу изменения объема . Поэтому полученное количество теплоты (dQ = dU + dA) будет равно . Сравнивая с формулой (1), получим, что молярная теплоемкость при изобарическом нагревании
В формулах теплоемкости R – универсальная газовая постоянная, i – число степеней свободы молекулы газа. Это число независимых координат, необходимых для определения положения молекулы в пространстве. Или это число компонент энергии, которыми обладает молекула. Например, для одноатомной молекулы это составляющие кинетической энергии при поступательном движении относительно трех координатных осей, i = 3. Для двухатомной молекулы добавляются еще кинетические энергии вращательного движения относительно двух осей, так как относительно третьей, проходящей через оба атома, момент инерции и энергия отсутствуют. В итоге двухатомная молекула имеет 5 степеней свободы. Точно так же и для воздуха, состоящего в основном из двухатомных молекул кислорода и азота.
Экспериментальноеизмерение молярной теплоемкости воздуха производится с помощью калориметра. В калориметре воздух нагревается при постоянном давлении, равном атмосферному. Измерение температуры при нагреве производится с помощью термопары, подсоединенной к мультиметру. Для повышения точности измерений следует нагревать большую массу воздуха. Поэтому с помощью компрессора воздух непрерывной струей пропускается через калориметр (рис. 1).
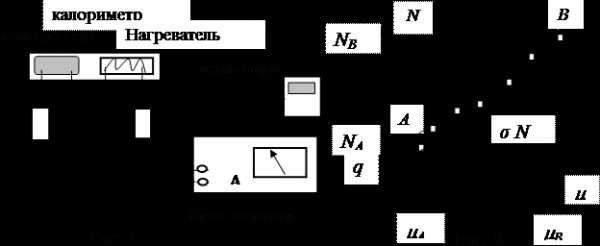 |
Нагреватель калориметра подключен к блоку питания. Потребляемая мощность определяется по показаниям вольтметра и амперметра N = J U. Когда после включения установки наступит тепловое равновесие и температура воздуха, выходящего из калориметра, перестанет изменяться, подводимая от электронагревателя тепловая мощность N расходуется на нагрев поступающего в калориметр воздуха и частично на теплопередачу q через стенки калориметра. Поэтому уравнение теплового баланса имеет вид
. (3)
Здесь m – секундный расход воздуха через калориметр, DT – повышение температуры воздуха после прохождения через калориметр.
Для исключения неизвестной мощности тепловых потерь q нужно провести опыты при разном расходе воздуха, но при одинаковом повышении температуры. При этом мощность тепловых потерь будет одинакова, потому что теплопередача через стенки пропорциональна перепаду температур. Согласно уравнению (3), подводимая к калориметру тепловая мощность, при постоянном повышении температуры воздуха Δ Т, зависит от секундного расхода воздуха линейно, и поэтому график – прямая линия. Угловой коэффициент линии равен . Его можно определить экспериментально по графику как отношение катетов прямоугольного треугольника, построенного на экспериментальной линии, по координатам его вершин А и В. Откуда получим
. (4)
ВЫПОЛНЕНИЕ РАБОТЫ
1. Измерить температуру воздуха в лаборатории термометром. Включить калориметр в сеть 220 В, установить переменным резистором компрессора сравнительно большой расход воздуха.
2. Установить переменным резистором нагревателя такую мощность, чтобы после установления теплового равновесия (3 мин) температура воздуха выходящего из калориметра повысилась бы на 30–50 К. Измерить температуру воздуха, определить по шкале резистора компрессора расход воздуха. Записать в таблицы повышение температуры, расход воздуха, показания амперметра и вольтметра.
3. Уменьшить расход воздуха примерно на одну пятую часть от начального и синхронно уменьшить мощность нагревателя так, чтобы температура воздуха на выходе из калориметра оставалась одинаковой. Эта часть работы требует терпения, плавности регулировки. Результаты измерений расхода воздуха, силы тока и напряжения записать в таблицу. Опыт провести не менее пяти раз во всем диапазоне расхода воздуха.
| Повышение температуры D Т, К | ||||||
| Расход воздуха m, г/с | ||||||
| Сила тока I, А | ||||||
| Напряжение U, В | ||||||
| Мощность N=IU, Вт |
Выключить питание мультиметров. Выключить установку.
4. Произвести расчеты. Определить мощность, потребляемую электронагревателем, N= I U. Записать в таблицу.
5. Построить график зависимости потребляемой мощности от расхода воздуха N (m). Размер графика не менее половины страницы. На осях координат нанести равномерный масштаб. Около точек провести прямую линию так, чтобы сумма отклонений точек была минимальной.
6. Построить на экспериментальной линии как на гипотенузе прямоугольный треугольник (рис. 2). Определить координаты вершин А и В треугольника. По формуле (4) рассчитать среднее значение молярной теплоемкости <CP>. Принять значение массы моля воздуха равным 28,9 10-3 кг/моль.
7. Оценить графическим методом случайную погрешность измерения молярной теплоемкости. Для этого провести на графике параллельно экспериментальной прямой две близкие линии так, чтобы все точки кроме промахов были между ними. Определить расстояние между линиями σN. Произвести расчет по формуле
. (5)
8. Записать результат в виде СР = <CP> ± d CP , P = 90%. Сравнить с теоретическим значением, рассчитанным по формуле (3), при R= 8,31 Дж/моль К, i = 5.
Сделать выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Дайте определение молярной теплоемкости вещества.
2. Сформулируйте первое начало термодинамики. Запишите формулы для теплоты, работы, внутренней энергии идеального газа.
3. Выведите формулы для молярной теплоемкости идеального газа при изохорическом и изобарическом нагревании.
4. Запишите уравнение теплового баланса для калориметра.
5. Объясните, почему тепловые потери через стенки калориметра не влияют на измерение теплоемкости.
6. Объясните, почему в установке воздух должен непрерывной струей проходить через калориметр.
Работа 16
Рекомендуемые страницы:
lektsia.com
Л.р.5 Определение отношения теплоемкостей
Цель работы: определение коэффициента Пуассона для воздуха методом адиабатического расширения.
Оборудование: стеклянный сосуд, жидкостный манометр, барометр, термометр, насос Шинца.
Вопросы теории
Теория теплоемкости идеального газа. Связь теплоемкостей с числом степеней свободы молекул газа. Адиабатический процесс и изопроцессы. Изображение газовых процессов на диаграммах (P,V), (P, T), (V, T). Применение первого начала термодинамики к процессам в идеальном газе.
Указания к теоретической подготовке
Согласно теории теплоемкости изменение внутренней энергии идеального газа зависит от числа степеней свободы молекул i и изменения температурыT:
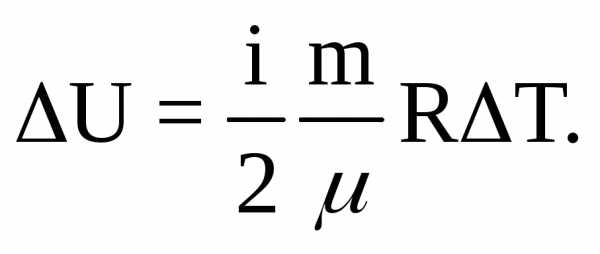
С другой стороны, по первому началу
термодинамики при изохорическом процессе
все подводимое количество теплоты 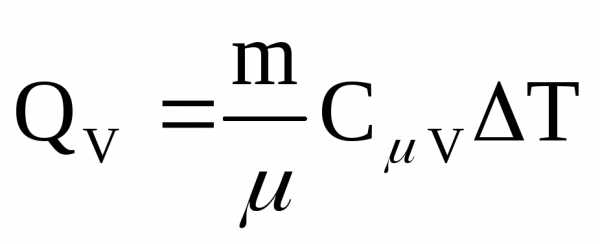 идет на приращение внутренней энергииU:
Qv=U
.
идет на приращение внутренней энергииU:
Qv=U
.
Отсюда следует, что молярная теплоемкость при постоянном объеме:
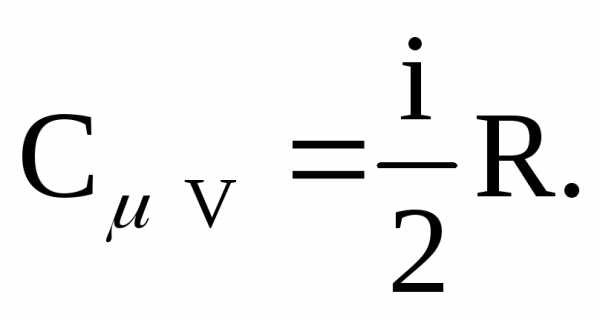
Применив первое начало к изобарическому
процессу и установив связь между
теплоемкостями С p и C v:;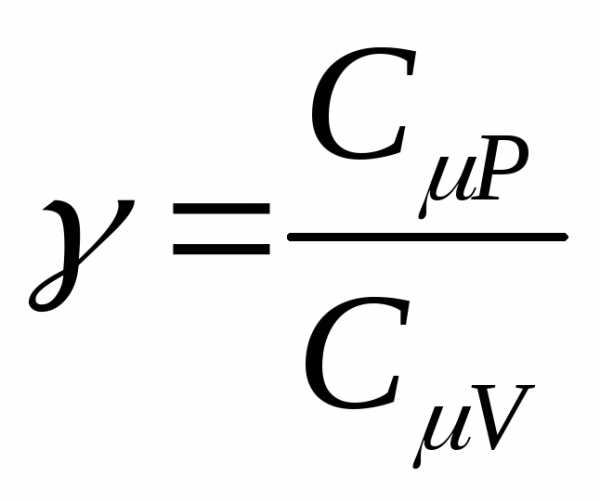 ,
,
можно найти показатель адиабаты через число степеней свободы молекул газа:
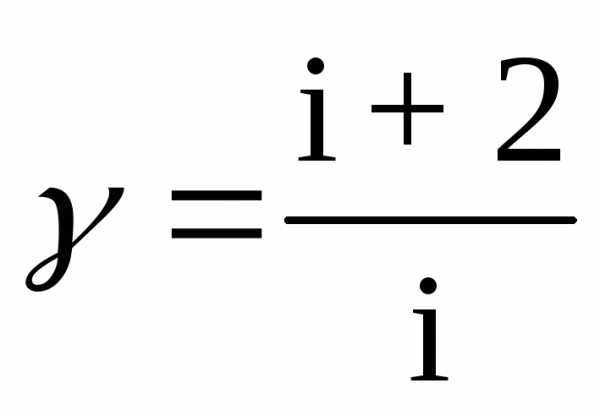 .
.
Число степеней свободы молекулы показывает, какое число координат нужно задать для однозначного определения положения молекулы в пространстве. Одноатомные свободные молекулы имеют три степени свободы, связанные с поступательным движением; жесткие двухатомные – пять степеней свободы: три поступательных и две вращательных; трехатомные – шесть: три поступательных и три вращательных. Воздух (смесь газов) состоит, в основном, из двухатомных газов, поэтому считают, что число степеней свободы воздуха равно пяти.
Описание установки и метода измерения
Установка состоит из стеклянного сосуда 1, закрытого пробкой, в которую вставлены клапан 4 и трубки для присоединения насоса и манометра.
С помощью насоса 2 в сосуде можно создать повышенное давление, измеряемое манометром 3. Через некоторое время вследствие теплообмена через стенки сосуда установится тепловое равновесие воздуха в сосуде с окружающей средой, воздух будет иметь комнатную температуру и находиться под давлением P1, превышающим атмосферное давление на величину, измеряемую манометром.
Если быстрым, кратковременным нажатием клапана дать воздуху из сосуда расшириться, то давление уменьшится до атмосферного (при этом уровни жидкости в правом и левом коленах манометра сравняются), а температура понизится. Через некоторое время из-за теплообмена с окружающей средой воздух в сосуде нагревается до комнатной температуры, давление повышается до P2.
Показания манометра перед адиабатическим расширением h1 и после изохорического нагревания h2 связаны с давлениями газа P1и P2, которые много меньше атмосферного P0, поэтому рабочую формулу можно получить в виде:
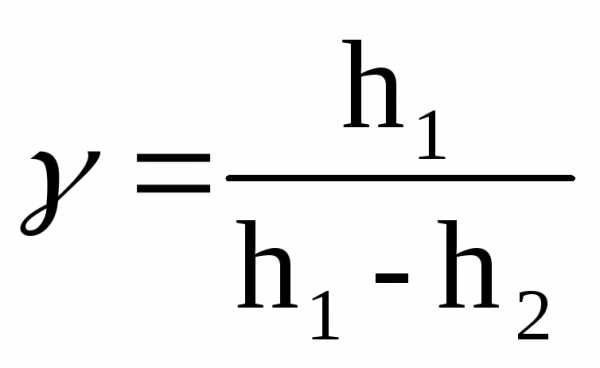
Задание 1. Экспериментальное определение показателя адиабаты
1. Накачать в сосуд воздух так, чтобы избыточное давление было не больше 25 см водяного столба. Дождаться установления теплового равновесия воздуха в сосуде с окружающей средой. Записать показания манометра h1перед адиабатным расширением.
2. Произведите быстрое расширение газа кратковременным нажатием клапана. Дождитесь установления равновесия после изохорического нагревания (в течение 5-7 минут) и запишите показание манометра h2.
3. Вычислите показатель адиабаты экс.по результатам опыта.
4. Повторите опыт 7-10 раз, для каждого опыта вычисляя экс..
5. Найдите среднее значение экс , вычислите погрешности измерений, запишите окончательный результат.
6. Вычислите значение показателя адиабаты через число степеней свободы его молекул. Сравните экситеор.
Задание 2*. Построение диаграмм процессов
1.В координатах (P,V), (P, T), (T, V) изобразите процессы, происходящие с некоторой массой воздуха в сосуде при выполнении пунктов 1, 2 задания 1.
2.Определите давление воздуха в сосуде в конце адиабатического расширения. На сколько градусов при этом понизилась температура воздуха в сосуде?
Контрольные вопросы
1. Что называют молярной теплоемкостью вещества? Удельной теплоемкостью вещества?
Молярная теплоемкость— скалярная величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1 К
где =m/М—количество вещества.
Единица молярной теплоемкости — джоуль на моль-кельвин (Дж/(моль К)).
Удельная теплоемкость вещества — скалярная величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К:
Единила удельной теплоемкости — джоуль на килограмм-кельвин (Дж/(кг К)).
2. Какая связь между Сp и Сv для идеального газа? Почему молярная теплоемкость при постоянном давлении Сp больше молярной теплоемкости при постоянном объеме Сv ?
Молярная теплоёмкость для идеального газа при постоянном давлении больше молярной теплоёмкости при постоянном объеме на величину универсальной газовой постоянной и зависит только от числа степеней свободы газа.
Т.е. для каждого идеального газа молярная теплоёмкость при постоянном объёме является величиной постоянной.
Отношение молярной теплоёмкости при постоянном давлении к молярной теплоёмкости при постоянном объёме называют показателем адиабаты – γ, или коэффициентом Пуассона.
3. Что понимают под числом степеней свободы i молекул газа? Числом степеней свободы материального объекта называют число независимых координат, которые необходимо задать, чтобы однозначно определить положение этого объекта относительно рассматриваемой системы отсчета. Например, положение материальной точки в пространстве определяется тремя координатами x, y, z, следовательно, материальная точка обладает тремя степенями свободы. Две материальные точки, находящиеся на неизменном расстоянии друг от друга (например, модель двухатомной молекулы с жесткой связью между атомами), имеют пять степеней свободы – три поступательные и две вращательные. Таким образом, двухатомная молекула может совершать пять независимых движений: три поступательных движения вдоль осей X, Y, Z и два вращения относительно осей X и Y (рис. 1). Опыт показывает, что вращение относительно оси Z, на которой лежат центры обоих атомов, может быть возбуждено только при очень высоких температурах. При обычных температурах вращение около оси Z не происходит, так же как не вращается одноатомная молекула.
4. Как связаны внутренняя энергия идеального газа и молярная теплоемкость с числом степеней свободы его молекул?
Числом степеней свободы i называют наименьшее число независимых координат, с помощью которых можно однозначно определить положение тела в пространстве.
При нагревании жидких и твердых тел их объем практически не изменяется, и работа расширения оказывается равной нулю. Поэтому все количество теплоты, полученное телом, идет на изменение его внутренней энергии. В отличие от жидкостей и твердых тел, газ в процессе теплопередачи может сильно изменять свой объем и совершать работу. Поэтому теплоемкость газообразного вещества зависит от характера термодинамического процесса. Обычно рассматриваются два значения теплоемкости газов: CV – молярная теплоемкость в изохорном процессе (V = const) и Cp – молярная теплоемкость в изобарном процессе (p = const). В процессе при постоянном объеме газ работы не совершает: A = 0. Из первого закона термодинамики для 1 моля газа следует QV = CVΔT = ΔU.
5. Какие процессы происходят с воздухом в сосуде при определении методом адиабатического расширения? Дайте определение этих процессов.
Одним из самых простых методов определения у для газов является метод адиабатического расширения (метод Клемана и Дезорма). Метод заключается в следующем. Если в некоторый сосуд, снабженный открытым манометром для измерения давления в этом сосуде и краном для соединения воздуха в сосуде с атмосферой, накачать при закрытом кране немного воздуха, то через некоторое время температура воздуха в сосуде станет равной комнатной Т01,давление p1 будет несколько выше атмосферного (первое состояние газа). Если затем открыть кран и закрыть его опять в тот момент, когда давление в сосуде станет равным атмосферному, то произойдет адиабатическое расширение оставшейся части газа в сосуде. В этом случае давление газа будет равно атмосферному р2, температура Т2 вследствие адиабатического расширения. будет ниже комнатной. Назовем это состояние газа вторым. С течением времени температура воздуха в сосуде будет повышаться и достигнет комнатной, давление повысится до значения р3, объем останется неизменным (третье состояние). Переход газа из первого состояния во второе происходит адиабатически и подчиняется уравнению Пуассона, которое в этом случае удобно записать в форме
6. Как с помощью манометра найти давление воздуха в сосуде; как перевести это давление в Паскали?
ЛИТЕРАТУРА [2, 6, 7, 8]
studfiles.net
Определение отношения теплоёмкостей воздуха. | Учителю.
Определение отношения теплоёмкостей воздуха.
ЦЕЛЬ: изучить процессы, протекающие в газе при определении отношения теплоёмкостей методом Клемана-Дезорма, и. измерить отношение Cр/Cv для воздуха.ОБОРУДОВАНИЕ: установка, состоящая из стеклянного баллона, манометра, компрессора, секундомер.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ.
Теплоемкостью вещества называется физическая величина, численно равная количеству теплоты, которое нужно ему сообщить, чтобы повысить температуру вещества на один кельвин.
Теплоемкость единицы массы называется удельной теплоемкостью, а теплоемкость одного моля вещества – молярной теплоемкостью.
где с и С – удельная и молярная теплоемкость,
– теплота, подводимая к системе,
dT – изменение температуры,
m – полная масса вещества,
– его молекулярная масса.
Величина теплоемкости для одного и того же вещества зависит как от агрегатного состояния, так и от условий его нагревания.
Нагревание вещества может происходить как при постоянном давлении, так и при постоянном объеме. Рассмотрим эти процессы.
а) P = const . Процесс изобарический.
Первое начало термодинамики для изобарического процесса имеет вид:
изменение внутренней энергии идеального газа:
Элементарная работа при равновесном изменении объема, вычисленная из уравнения состояния газа:
Из выражений (1.1), (1.2), (1.3), (1.4) получаем для молярной теплоемкости при постоянном давлении:
где: i – число степеней свободы молекул газа – это число независимых координат, определяющих положение молекулы в пространстве: i =3 для одноатомной, i=5 для двухатомной, i=6 для трёх- и многоатомной;
R = 8,31 Дж/моль. R – универсальная газовая постоянная.
б) V = const . Процесс изохорический.
Первое начало термодинамики для изохорического процесса
т.е. вся подводимая теплота идет только на изменение внутренней энергии системы. С учетом выражения (1.1) и (1.3) имеем
таким образом, теплоемкость идеального газа зависит только от рода газа ( i ) и от вида процесса.
в) В технике при анализе тепловых процессов и циклов как правило нет необходимости вычислять или экспериментально определять по отдельности теплоемкости при постоянном давлении Ср и при постоянном объеме Сv. Вычисление и измерение их связано с определенными трудностями (многокомпонентный газ, ничтожная масса газа по сравнению с сосудом, его содержащим и т.д.).
Во многих случаях достаточно знания только их отношения:
где – называют показателем адиабаты или коэффициентом Пуассона.
Адиабатическим называется процесс, протекающий без теплообмена с окружающей средой.
Из 1 начала термодинамики для адиабатического процесса следует:
т.е. газ расширяясь совершает работу против внешних сил за счет уменьшения своей внутренней энергии.
В выражении (2.7) работа выражена через изменение температуры, а так как в эксперименте измеряется давление, то произведем изменение параметров.
Из уравнения состояния имеем подставим в уравнение (2.7)
Учитывая, что и из выражения (2.3) следует:
Окончательно получаем:
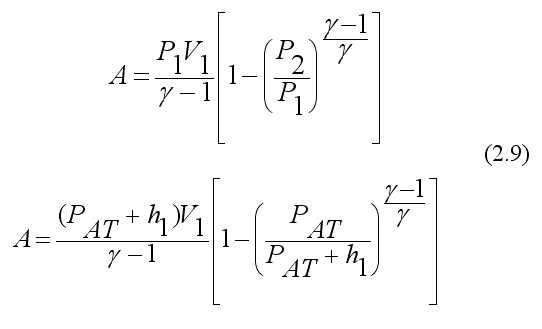
ОПИСАНИЕ УСТАНОВКИ И МЕТОДА ИЗМЕРЕНИЙ
 Измерения выполняют на установке (рис. 1), состоящей из большого стеклянного баллона Б, насоса Н и водяного манометра 1. Баллон соединяют краном К с насосом, а краном K0 – с атмосферой.
Измерения выполняют на установке (рис. 1), состоящей из большого стеклянного баллона Б, насоса Н и водяного манометра 1. Баллон соединяют краном К с насосом, а краном K0 – с атмосферой.
Метод, предложенный Клепаном и Дезормом (1819 г.), основан на изучении параметров некоторой массы газа, переходящей из одного состояния в другое двумя последовательными процессами: адиабатическим и изохорическим.
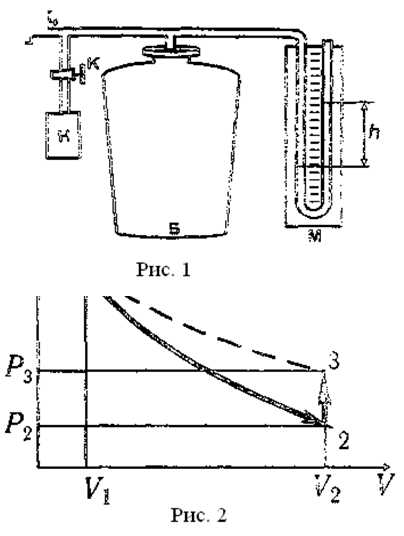
Эти процессы на диаграмме P—V (рис.1) представлены кривыми 1-2 и 2-3 соответственно. Если накачать воздух в баллон и выдержать до установления теплового равновесия с окружающей средой, то в этом начальном состоянии 1 газ имеет параметры Р1, V1, T1 причём температура газа в баллоне равна температуре окружающей среды, а давление Р1=Р0+P’ немного больше атмосферного Р0.
При открывании крана К0 воздух в баллоне перейдёт в состояние 2. Его давление снизится до атмосферного Р2=Р0. Оставшаяся масса воздуха, которая занимала в состоянии 1 часть объёма баллона, расширяясь, займёт весь объем V2. При этом температура воздуха, оставшегося в баллоне, уменьшится. При быстром расширении газа можно пренебречь его теплообменом с окружающей средой через стенки баллона и считать процесс 1-2 адиабатическим:
После закрытия крана Ко охлаждённый адиабатическим расширением воздух в баллоне будет нагреваться (процесс 2-3) до температуры окружающей среды T3=T1 при постоянном объёме V2= V3 При этом давление в баллоне возрастёт до Р3=Р2+Р”
Избыточное давление воздуха P’ и P’’ измеряют с помощью U-образного манометра по разности уровней жидкости с плотностью р:
где H и h — показания манометра в состояниях 1 и 3 соответственно.
Тогда
Состояния воздуха 1 и 3 принадлежат – изотерме, поэтому:
Исключив отношение объёмов из уравнений (7) и (9), найдём связь давлений газа:
Выразим давления P1 и P2 через P0 с учётом (8.8) к прологарифмируем:
С учётом того, что если x<<1. тс ln(1+х)= x, получим расчётную формулу в следующем виде:
Таким образом, для определения отношения теплоёмкостей воздуха достаточно осуществить процессы (1-2-3) и измерить показания манометра Н и h в состояниях газа 1 и 3 соответственно.
Но осуществить равновесный адиабатический процесс сложно: если проводить расширение газа быстро, то процесс не будет равновесным, так как температура и давление газа не успевают выравниваться по объёму. Для проведения медленного адиабатического процесса нужна тепловая изоляция баллона. 3 данной установке за время / расширения газа подводится тепло. Поэтому при последующем изохорическом нагревании давление поднимается меньше, т.е. измеряемое h’ По мере увеличения времени расширения газа значение h’ снижается, приближаясь к нулю при t → ∞ (изотермическое расширение 1-3), Опытным путем установлено, что
Логарифмируя эту функцию, получаем зависимость
где а – постоянная установки,
t – время протекания процесса, в течение которого баллон сообщается с атмосферой. График зависимости (11) конечного избыточного давления воздуха в баллоне от времени контакта его с атмосферой показан на рис. 3.
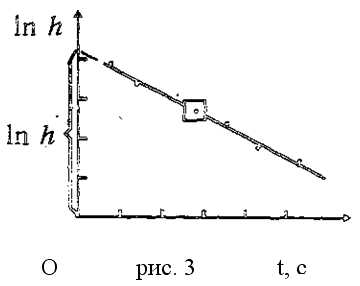
Построив по данным эксперимента такой график, можно путём экстраполяции опытной прямой до t=0 – определить значение In h, а по нему значение h, необходимое для расчёта по формуле (10).
Контрольные вопросы
1. Что называют: а) теплоёмкостью тела; б) удельной теплоёмкостью газа; в) молярной теплоёмкостью газа? В каких единицах их измеряют?
2. От чего зависят эти теплоёмкости?
3. Каковы величины молярных теплоёмкостей Ср и Сv для воздуха? Чем объясняется, что Ср> Сv?
4. Для каких теплоёмкостей справедливы соотношения Cp = C v+ R ?
5. Что называют числом степеней свободы молекулы?
6. Каковы значения показателя адиабаты а) для двухатомного; б) для трехатомного и многоатомного идеального газа?
7. Для какого газа: одноатомного ели двухатомного – график адиабаты более крутой?
8. Запишите первое начало термодинамики для адиабатического процесса.
9. Какие процессы описываются уравнениями: PV = const;
10. Как изменяется температура и давление газа: а) при адиабатическом
расширении; б) при адиабатическом сжатии?
11. В каких состояниях из указанных на диаграмме (рис. 2, с. 89) воздух в баллоне: а) имеет комнатную температуру; б) находится при атмосферном давлении?
12. Какой процесс совершается при открывании крана K2, если в баллоне было избыточное давление воздуха?
13. Какой процесс происходит после адиабатического расширения газа при проведении опыта?
14. Какие величины измеряют в работе для расчёта показателя адиабаты ?
15. По какой формуле определяют значение отношения теплоемкостей а) опытное; б) теоретическое?
testent.ru
Теплоемкость воздуха: таблица
Теплоемкость как физическая величина показывает количество тепловой энергии, которое необходимо для изменения температуры рабочего тела, в данном случае, воздуха, на один градус. Теплоемкость воздуха непосредственно зависит от температуры и давления. При этом для исследования разных видов теплоемкости могут применяться различные методы.
Математически теплоемкость воздуха выражается как отношение количества тепла к приращению его температуры. Теплоемкость тела, имеющего массу 1 кг, принято называть удельной. Молярная теплоемкость воздуха – теплоемкость одного моля вещества. Обозначается теплоемкость – Дж/К. Молярная теплоемкость соответственно Дж/(моль*К).
Теплоемкость можно считать физической характеристикой какого-либо вещества, в данном случае воздуха, в том случае, если измерение проводится в постоянных условиях. Чаще всего подобные измерения проводятся при постоянном давлении. Так определяется изобарная теплоемкость воздуха. Она возрастает с увеличение температуры и давления, а также является линейной функцией данных величин. В этом случае изменение температуры происходит при постоянном давлении. Для расчета изобарной теплоемкости необходимо определить псевдокритическую температуру и давление. Она определяется с использованием справочных данных.
Теплоемкость воздуха. Особенности
Воздух представляет собой газовую смесь. При их рассмотрении в термодинамике приняты следующие допущения. Каждый газ в составе смеси должен быть равномерно распределен по всему объемы. Таким образом, объем газа равен объему всей смеси. Каждый газ в составе смеси обладает своим парциальным давлением, которое он оказывает на стенки сосуда. Каждый из компонентов газовой смеси должен иметь температуру, равную температуре всей смеси. При этом сумма парциальных давлений всех компонентов равняется давлению смеси. Расчет теплоемкости воздуха выполняется на основе данных о составе газовой смеси и теплоемкости отдельных компонентов.
Теплоемкость неоднозначно характеризует вещество. Из первого закона термодинамики можно сделать вывод, что внутренняя энергия тела изменяется не только в зависимости от количества полученного тепла, но и от совершенной телом работы. При различных условиях протекания процесса теплопередачи, работа тела может различаться. Таким образом, одинаковое сообщенное телу количество теплоты, может вызвать различные по значению изменения температуры и внутренней энергии тела. Эта особенность характерна только для газообразных веществ. В отличие от твердых и жидких тел, газообразные вещества, могут сильно изменять объем и совершать работу. Именно поэтому теплоемкость воздуха определяет характер самого термодинамического процесса.
Однако при постоянном объеме воздух не совершает работу. Поэтому изменение внутренней энергии пропорционально изменению его температуры. Отношение теплоемкости в процессе с постоянным давлением, к теплоемкости в процессе с постоянным объемом является частью формулы адиабатного процесса. Оно обозначается греческой литерой гамма.
Из истории
Термины «теплоемкость» и «количество теплоты» не очень удачно описывают свою суть. Связано это с тем, что они пришли в современную науку из теории теплорода, которая была популярна в восемнадцатом веке. Последователи этой теории рассматривали теплоту как некое невесомое вещество, которое содержится в телах. Это вещество не может быть ни уничтожено, ни создано. Охлаждение и нагревание тел объясняли уменьшением или увеличением содержания теплорода соответственно. Со временем эта теория была признана несостоятельной. Она не могла объяснить, почему одинаковое изменение внутренней энергии какого-либо тела получается при передаче ему разного количества теплоты, а также зависит от совершаемой телом работы.
autogear.ru