Основные параметры воздуха
Состав воздуха. Атмосферный воздух представляет собой механическую смесь различных газов, составляющих сухую его часть, и некоторого количества водяных паров. Водяной пар обычно находится в ненасыщенном (перегретом) состоянии, но может переходить в насыщенное и перенасыщенное состояние (туман). Состав газов в сухой части воздуха отличается сравнительно большим постоянством.
Смесь сухой части воздуха и водяных паров называется влажным воздухом. В используемом при кондиционировании диапазоне температур и давлений влажный воздух можно рассматривать как идеальный газ, следующий законам Бойля–Мариотта, согласно которому занимаемый газом объем и его давление связаны соотношением pi/ps = Vs/Vi, и Гей-Люссака, когда объемы газов при постоянном давлении пропорциональны абсолютным температурам.
Свойства насыщенного водяного пара описываются сложными зависимостями, поэтому на практике для определения р и Т пользуются таблицами физических свойств этого пара (например, по проф. М. П. Вукаловичу).
Температура воздуха показывает степень его нагрева. В технике кондиционирования воздуха для измерения температуры воздуха пользуются термометрами, имеющими стоградусную шкалу Цельсия (t, °С) и абсолютную шкалу Кельвина (Т, К). Соотношение между этими шкалами выражается зависимостью
Т = 273,15 +t.
Давление воздуха. Согласно закону Дальтона общее давление смеси равно сумме парциальных давлений нескольких газов, образующих эту смесь, т. е.
Р = Pi + Pt + Ps + • • • + Рп = Рп-1
Так как влажный воздух представляет собой паровоздушную (бинарную) смесь, то общее давление атмосферного воздуха, или барометрическое давление, равно сумме парциальных давлений сухой его части и водяных паров:
рб = рс + Рп.
В расчетах процессов кондиционирования воздуха давление атмосферного воздуха и водяных паров обычно измеряются в миллиметрах ртутного столба.
Давление может быть выражено также высотой столба какой-либо другой жидкости, масса которой уравновешивает это давление. Одна техническая атмосфера, равная 1 кгс/см2, уравновешивается столбом ртути высотой 735,6 мм или водяным столбом высотой примерно 10 м. За нормальное атмосферное давление принята одна физическая атмосфера, равная 760 мм рт. ст. при 0°С или 10,333 м вод. ст.
Влагоемкость воздуха, г/кг–это масса водяного пара, содержащегося во влажном воздухе при полном его насыщении, отнесенная к массе сухой его части.
Относительная влажность воздуха (в технических расчетах – это отношение массы водяных паров во влажном воздухе к массе водяных паров в воздухе при той же температуре и полном насыщении. Относительную влажность обычно выражают в процентах.
Иногда относительную влажность воздуха (выражают отношением фактического (ненасыщенного) состояния парциального давления водяных паров в воздухе к парциальному давлению водяного пара в насыщенном состоянии при той же температуре:
Температура точки росы tp, или просто точка росы, – это такая температура, до которой надо охладить влажный (ненасыщенный) воздух, чтобы он стал насыщенным (tр=100%) при сохранении постоянного влагосодержания. Это наинизший предел охлаждения температуры воздуха при постоянном влагосодержании.
Температура воздуха по мокрому термометру tм–это температура насыщенного воздуха в условиях испарения воды при сохранении постоянной энтальпии, равной начальной.
Удельная или массовая, теплоемкость воздуха с – это количество тепла, потребное для нагревания 1 кг воздуха на 1 °С.
Удельная теплоемкость сухого воздуха при постоянном давлении зависит от температуры.
Для процессов, происходящих в СКВ в интервале температур от –50 до +50°С и при практически неизменяемом общем давлении влажного воздуха, удельная теплоемкость сухого воздуха может быть принята постоянной и равной Сс=0,24 ккал/(кг°С).
Удельную теплоемкость влажного воздуха следует рассматривать как теплоемкость смеси, состоящей из 1 кг сухого воздуха и 0,001d кг водяного пара. В связи с незначительной массой водяного пара, приходящейся на 1 кг сухого воздуха, удельную теплоемкость влажного воздуха в практических расчетах принимают равной удельной теплоемкости сухого воздуха = 0,24ккал/(кг°С).
Энтальпия влажного воздуха †в–это количество тепла, находящееся во влажном воздухе, сухая часть которого имеет массу 1 кг†
Масса воздуха. Плотность, или объемная масса, влажного воздуха † – это масса его в 1 м3.
†ри одном и том же барометрическом давлении объемная масса влажного воздуха меньше, чем сухого.
При температурах, обычно встречающихся в практических расчетах кондиционирования воздуха, разница в массе влажного воздуха и сухой части его незначительна (1%).
ЛЕКЦИЯ №16
1–D-ДИАГРАММА
1–d -диаграмма, разработанная проф. Л. К. Рамзиным в 1918 г., представляет собой графическую интерпретацию уравнения энтальпии влажного воздуха. Диаграмма строится в косоугольной системе координат, где ось ординат проведена вертикально, а ось абсцисс – под углом 135° к ней. По оси ординат отложены значения энтальпии, а по оси абсцисс – влагосодержания влажного воздуха d на 1 кг сухого.
Для удобства отсчета влагосодержаний и сокращения размеров диаграммы наклонная ось абсцисс на диаграмме не вычерчивается, а вместо нее через начало координат проводится вспомогательная горизонтальная линия, на которой откладываются значения влагосодержаний (в произвольном масштабе). Через полученные точки проводятся вертикали, представляющие собой линии постоянного влагосодержания d=const. На оси ординат (также в любом масштабе) откладываются значения энтальпии, причем вверх от точки О откладываются положительные, а вниз – отрицательные значения. Через полученные точки параллельно оси абсцисс проводятся линии постоянной энтальпии 1=const.
Необходимо иметь в виду, что изотермы между собой не параллельны, так как угол наклона их к горизонтальной оси различен. При низких температурах непараллельность изотерм почти незаметна.
Для построения линий φ=const на каждой изотерме определяют точки, имеющие степень насыщения воздуха φ =5, 10, 20,…, 100%. Соединяя на разных изотермах точки с одинаковой степенью насыщения, получим линии φ =const, имеющие вид расходящихся кривых. Нижняя кривая φ =100% характеризует насыщенное состояние воздуха и называется пограничной кривой.
При повышении барометрического давления линия насыщения на /–d-диаграмме смещается вверх, а при понижении – вниз. При изменениях барометрического давления в пределах ±7,5 мм рт. ст. изменения параметров воздуха будут незначительны, и их можно не учитывать. Однако при больших изменениях барометрического давления изменения параметров воздуха будут значительными.
Для построения линии парциального давления пара с правой стороны диаграммы на прямой, параллельной оси ординат, наносится шкала парциальных давлений в миллиметрах ртутного столба, начиная с рп=0 до возможного значения рп в диапазоне данной диаграммы. Масштаб этой шкалы выбирается крупнее, но с таким расчетом, чтобы линия рп не пересекалась с кривой φ =100% (1 мм=0,125–0,25мм рт.ст.).
Для построения линии парциального давления пара из точек пересечения изотерм с кривой φ =100% опускают перпендикуляры на вспомогательную горизонтальную линию. От этой линии вверх в принятом масштабе откладываются парциальные давления водяных паров, насыщающих воздух при данных температурах, которые определяют по таблицам. Через найденные точки проводится линия парциального давления водяного пара.
Условимся в дальнейшем в единицах энтальпии и влагосодержания опускать слова «сухого воздуха».
studfiles.net
Воздух сухой, физические параметры – Энциклопедия по машиностроению XXL
Воздух сухой, физические параметры 291 Воздухоподогреватели 357, [c.719]Так как в продуктах сгорания (газа) ГТУ содержится значительное количество воздуха, то физические параметры газа определяют по таблицам сухого воздуха
Физические параметры сухого воздуха и воды берут из таблиц. [c.513]
Физические параметры сухого воздух при давлении 101 320 н1м [c.544]
| Таблица 4. Физические параметры сухого воздуха при нормальном давлении | 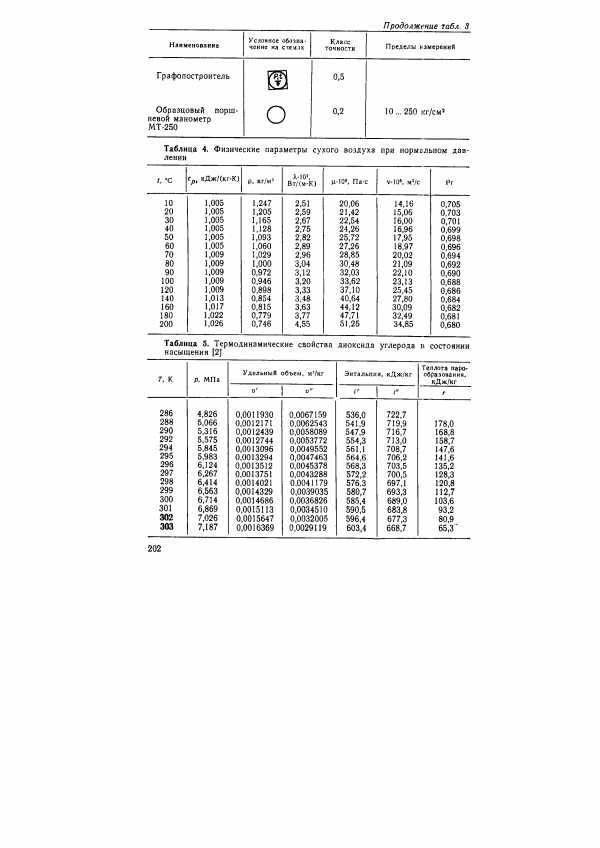 |
Физические параметры для сухого воздуха при нормальном атмосферном давлении (Р(,==Ю1,325 к1Ь [c.431]
Физические параметры сухого воздуха при постоянном давлении 980 гПа — см. также рис, 28, 29 [c.69]
Физические параметры сухого воздуха при р = I кГ[см. (коэффициенты вязкости и теплопроводность, приняты по данным ВТИ) [II] [c.212]
ПРИЛОЖЕНИЕ I Физические параметры сухого воздуха при р = 1 к.г/см [c.318]
Физические параметры сухого воздуха при р = 1 кГ/см [c.93]
ПРИЛОЖЕНИЕ V ФИЗИЧЕСКИЕ ПАРАМЕТРЫ ДЛЯ СУХОГО ВОЗДУХА ПРИ 101,3 кн м” (760 мм рт. ст.) [c.351]
Физические параметры для сухого воздуха при давлении 760 мм рт ст, [20] [c.281]Физические параметры для сухого воздуха при/> = 760 лл/ от. ст. [c.384]
Физические параметры сухого воздуха при //= 760 мм рт. ст. [c.193]
Физические параметры сухого воздуха ири давлении 101 325 н. м [c.163]
В табл. 2 приведены физические параметры сухого воздуха при давлении Н = 760 мм рт. ст. [c.32]
Воздух сжатый — Температура 2 — 57 —— сухой — Параметры физические [c.405]
Термодинамические свойства сухого воздуха и водяного пара различны, поэтому Boii xBa влажного воздуха зависят от их количественного соотношения. Физические свойства влажного воздуха характеризуются следуюши ми параметрами парциальным давлением водяного пара влагосодержанием d, абсолютной рп и относительной ф влажностью, степенью насыщения ij . удельной энтальпией г, удельной теплоемкостью с, ]]лотностью
При проведении эксперимента широко варьировались (один-два порядка) физические, гидродинамические и геометрические параметры. Так, температура воды менялась от 2,2 до 88,7°С, т. е. почти от температуры плавления — затвердевания до температуры кипения (в максимальном диапазоне). Температура входящего в аппарат воздуха или газа по сухому термометру менялась от отрицательных значений (—5,2°С) до температуры выхлопных газов дизеля 525°С температура выходящего воздуха или газов по смоченному термометру — от 4,2 до 73,6 °С. Давление менялось от сотых долей атмосферного 9 кПа (0,09 кгс/см ) до значении выше атмосферного—118 кПа (1,21 кгс/см ). Скорость газа менялась от десятых долей единицы 0,7 м/с до околозвуковой 300 м/с (число Маха 0,9). Влагосодержание газа менялось от единиц до сотен граммов на килограмм для входящего газа — от 3,6 до 46, для выходящего — от 4,3 до 401 г/кг. Отношение массовых расходов жидкости и газа (коэффициент орошения) менялось от 0,33 до 80. Внутренний диаметр и высота газонаправляющей решетки ЦТА менялись соответственно от 0,05 до 0,5 м и от 0,002 до 0,3 м. [c.79]
mash-xxl.info
Основные физические свойства воздуха — МегаЛекции
Глава I. ОСНОВЫ АЭРОДИНАМИКИ КРЫЛА
Основные параметры воздуха
В состоянии неподвижности воздух характеризуется следующими параметрами: давление (Р), температура (Т) и плотность (ρ).
Давление — сила, перпендикулярно действующая на единицу поверхности. За единицу давления принято давление, равное одному килограмму на один квадратный сантиметр (кг/см2), эта величина называется технической атмосферой.
Давление, вызываемое массой вышележащих слоев воздуха, называется атмосферным давлением и обычно измеряется в миллиметрах ртутного столба. Давление в 1 кг/см2 уравновешивается столбом ртути высотой в
735,6 мм
где β— атмосферное давление, мм рт. ст.
Температура характеризует скорость хаотического движения молекул; чем больше температура, тем быстрее движутся молекулы, и наоборот.
Измерение температуры производится по шкале Цельсия и Кельвина. За 0° по шкале Цельсия принята температура таяния льда, а за 100° — температура ки-
пения воды при давлении 760 мм рт. ст. За 0° по шкале Кельвина принята температура —273° С. При этой температуре прекращается движение молекул газа.
Температура в градусах Цельсия обозначается —
tС, а в градусах Кельвина — Т° К:
Плотность воздуха –это масса, заключенная в единице объема. Она определяется по формуле
где m — масса, кг; V — объем, м3.
Все эти параметры воздуха связаны между собой уравнением состояния газа. Для воздуха, средний молекулярный вес которого (М) равен 29, уравнение имеет такой вид:
где Р — давление, кг/м2; ρ — массовая плотность воздуха, кг•с2/м4.
Из уравнения состояния газа вытекают, как частные случаи, известные законы Бойля—Мариотта и Гей-Люс-сака, открытые в свое время опытным путем. Так, при неизменной температуре давление пропорционально плотности, то есть обратно пропорционально объему, занимаемому определенной массой газа (закон Бойля— Мариотта)!
Если нагревать газ при постоянном давлении; то про
изведение остается неизменным. Это означает, что объ
ем газа растет пропорционально абсолютной температу
ре (закон Гей-Люссака). ;
Пользуясь уравнением состояния газа, можно, зная любые два показателя (параметра), вычислить Третий. Пусть, например, температура воздуха равна 15е С, а давление 760 мм рт. ст., что соответствует 10332 кг/м2 (1 мм рт. ст. ≈ 13,6 мм вод. ст.=13,6 кг/м2). Тогда можно определить плотность газа:
Такие расчеты представляют практический интерес, так как давление и температура могут быть просто измерены приборами, в отличие от плотности.
Основные физические свойства воздуха
Воздух характеризуется следующими физическими свойствами: цвет, прозрачность, электропроводимость, звукопроводимость, инертность, вязкость, сжимаемость.
При движении крыла в воздухе возникают силы, которые называют аэродинамическими. Их образование связано с такими физическими свойствами воздуха, как инертность, сжимаемость и вязкость.
Инертностью называется стремление тела сохранять состояние покоя или прямолинейного и равномерного движения. Мерой инертности тела является масса. Инертность воздуха оценивается его массовой плотностью, с увеличением которой инертность воздуха возрастает.
Сжимаемостью называется свойство среды увеличивать свою массовую плотность при повышении давления и уменьшать плотность при его понижении. Сжимаемость характеризуется отношением изменения плотности
к изменению давления , то. есть величиной
Чем больше это отношение, тем больше сжимаемость, и
наоборот.
Вязкостью называется свойство среды сопротивляться сдвигу одних ее слоев относительно других (соседних), проявляющееся в возникновении между слоями внутреннего трения.
Вязкость присуща различным средам. Однако природа вязкости жидкости и газа различна. У жидкости вязкость обусловлена сцеплением молекул. Поэтому, например, при нагревании, когда силы сцепления ослабевают, вязкость жидкости уменьшается (скажем, вязкость масла в двигателе).
Вязкость воздуха объясняется обменом молекулами между соседними слоями. Выделим в, воздушном потоке
Рис. 1. Внутреннее трение в воздухе
два параллельных направлению движения очень тонких слоя, расстояние между серединами которых равно (рис. 1), причем средняя скорость одного из них больше средней скорости другого на величину На-
ходясь в беспорядочном движении, молекулы из слоя 1 попадают в слой 2 и, теряя там избыток скорости
, стремятся ускорить движение слоя 2, а более «медленные» молекулы из слоя 2, попадая в слой 1, притормаживают его движение. Нагрев воздуха ускоряет беспорядочное движение молекул и усиливает обмен ими между слоями, ввиду чего внутреннее трение возрастает, а не уменьшается, как в жидкости.
Если поверхность, разделяющую слои 1 и 2, пересекают только беспорядочно движущиеся молекулы, а не целые струйки, то сила внутреннего трения между этими слоями, приходящаяся на 1 м2 разделяющей поверхности, выражается следующей формулой
■ ■
где µ, — коэффициент вязкости,зависящий только от температуры воздуха; при повышении температуры от 20 до 180°С он увеличивается более чем на 30%. Отно-
шение называется градиентом скорости и характе-
ризует интенсивность изменения скорости поперек на-правления движения. Чем резче нарастает скорость от слоя к слою, тем сильнее между ними трение.
Инертность воздуха в воздушном потоке, Уравнение расхода. Закон Бернулли
Из определения термина «инертность» вытекает, что инертность воздуха, рассматриваемого как сплошная среда, может проявиться лишь в том случае, когда, его частицы; испытывают изменения величины или сопротивления скорости. При этом инертность проявляется в виде понижения или повышения давления.
Закон постоянного секундного расхода воздуха является важнейшим законом теоретической аэродинамики. Он формулируется так: при установившемся движении газа через любое поперечное сечение данной струйки за одну секунду проходит одна и та же масса газа (рис. 2).
Поскольку
но, так как мы рассматриваем уравнение при малых скоростях (дозвуковых), когда воздух несжимаем, то
Из данного уравнения вытекает очень важный практический вывод: чем меньше поперечное сечение данной струйки, тем скорость воздуха в нем больше, и наоборот, чем больше поперечное сечение струйки, тем скорость в нем меньше.
По частицы воздуха обладают инертностью (имеют массу) и, в соответствии со вторым законом Ньютона, могут получать ускорение только под действием силы, направленной в сторону движения. Значит, на рассматриваемом участке струи давление в сечении I должно быть больше, чем в II. Итак, наименьшее давление получается там, где скорость наибольшая, и наоборот. В этом состоит сущность закона Бернулли.
Если предположить, что обмена энергией между струей воздуха и окружающей средой в сечениях I и II нет, то сумма всех видов энергии воздуха в сечении I равна сумме всех видов энергии в сечении II, то есть:,.
где полная энергия — сумма кинетической и
потенциальной энергий.
При условии, что через сечения I и II проходит масса воздуха в 1 м3, кинетическую энергию
Рис. 2, К уравнению расхода: F1,F2 — поперечные сечения; ρ1 ρ2— плотность; m1, m2 — масса воздуха, проходящая через сечение за секунду
можно выразить произведением плотности (ρ) на квадрат скорости, так как масса 1 м3 воздуха есть его плотность
Потенциальная энергия состоит из энергии давления, тепловой энергии и энергии силы веса. При условии, что воздух несжимаем, между струйкой и внешней средой отсутствует теплообмен, а энергией силы веса за незначительностью ее можно пренебречь, потенциальная энергия 1 м3 воздуха будет равна статическому давлению (Рсг). Произведя соответствующую замену, мы получим уравнение Бернулли для газа и жидкости без учета сжимаемости:
Величина называется скоростным напором
Из уравнения следует, что сумма скоростного напора и статического давления одинакова во
всех сечениях потока идеального несжимаемого воздуха
и есть величина постоянная,
Уравнение Бернулли широко используется для вычисления картины распределения давления на поверхности крыла, при определении скорости полета с помощью приемников воздушного давления и при решении
других задач гидравлики, гидротехники и аэродинамики. При больших скоростях движения потока, порядка 0,6 от скорости звука и более, пользуются более сложной формулой уравнения Бернулли, учитывающей сжимаемость воздушной среды.
Краткая характеристика атмосферы Земли
Атмосфера Земли имеет сложную структуру. Основными ее слоями являются тропосфера, стратосфера и ионосфера. Это разделение основано на учете как физических свойств отдельных слоев, так и характера их изменения с высотой.
Тропосфера— ближайший к поверхности земли слой
атмосферы. Ее толщина около 8—10 км над полюсами,
16—18 км над экватором и изменяется в зависимости от
времени года, температуры и характера подстилающей
поверхности, а также от характера атмосферных про
цессов.
Все характеристики тропосферы испытывают суточные и годовые изменения, обусловленные вращением Земли вокруг оси и обращением ее вокруг Солнца. Тропосфера, особенно ее нижняя половина, является слоем, где протекают и развиваются все жизненные биологические процессы. Здесь же в основном проводится в настоящее время и работа парашютистов. В тропосфере сосредоточен почти весь водяной пар и здесь осуществляется непрерывный его круговорот (испарение, конденсация и кристаллизация с облакообразованием). Температура (t), атмосферное давление (Р) и плотность (ρ) воздуха понижаются с высотой (температура в среднем на 6,5° С на каждый километр, давление в среднем на 1мм через каждые 10 м).
Между слоями тропосферы и стратосферы лежит
тонкий слой, называемый тропопаузой.
Стратосфера— слой атмосферы над тропопаузой при
мерно до высоты 82—83 км. Характеризуется более мед
ленным изменением температуры с высотой, чем в тро
посфере. Стратосферу подразделяют на нижнюю (До
высоты 32—40 км) и верхнюю, простирающуюся от это
го уровня до 82—83 км.
Нижняя стратосфера характеризуется зимой (по
крайней мере, в средних и высоких широтах) медленным
 |
понижением температуры с высотой (2° или несколько менее на 1 км), а летом таким же медленным ее ростом. Поэтому нижнюю стратосферу рассматривают как изометрический слой.
Верхняя стратосфера более сложна по термической структуре, так как включает в себя слой с повышенным содержанием озона (03) —озоносферу, начинающуюся примерно от 17—20 км и простирающуюся до 50—55 км. Сильное поглощение озоном ультрафиолетовой радиации солнца обусловливает значительное повышение температуры, особенно в верхней ее части (примерно от 35 до 55 км) до максимального значения около 80° С на высоте приблизительно 55 км. Выше начинается постоянное понижение температуры (в среднем 4,4° С на каждый километр). В результате на высоте 82—83 км температура достигает примерно —35° С. На верхней границе этого холодного слоя плавают серебристые облака, что говорит о начале (уже в ионосфере) устойчи-вого роста температуры воздуха с высотой.
Ионосфера — слой атмосферы, расположенный на высоте примерно от 80 до 500 км и содержащий большое количество заряженных электричеством частичек, называемых ионами. Это ионизированные молекулы и атомы атмосферных газов и свободные электроны. Они создают очень высокую проводимость воздуха, что ведет к преломлению, отражению, поглощению и поляризации радиоволн. В частности, это обусловливает слышимость радиосигналов даже незначительной мощности на большие расстояния.
В ионосфере наблюдаются полярные сияния, свечения ночного неба, а также магнитные бури.
Температура в ионосфере растет с высотой до очень больших значений, что обусловлено высокими скоростями движения ионизированных молекул и атомов атмосферных газов и свободных электронов (кинетическая температура). Ниже приводится схема строения атмосферы Земли с кривыми изменения температуры (t°С), давления (Рст), направления и скорости перемещения воздушных масс (рис. 3).
Рис. 3. Схема строения атмосферы Земли
Стандартная атмосфера
Температура и давление, а следовательно, и плотность воздуха, окружающего земной шар, зависят от ряда факторов.
Чем больше высота, тем меньше вес столба выше расположенного воздуха, а значит, меньше давление. Это обстоятельство используется при измерении в полете высоты барометрическим высотомером: та или иная высота соответствует определенному давлению воздуха.
Уменьшение давления сопровождается и уменьшением плотности (Р = 286 ρТ), причем темпы снижения этих показателей по мере увеличения высоты не совпадают, потому что одновременно изменяется и температура воздуха. Температура и давление воздуха на данной высоте зависят от географических координат, времени года и суток, от погоды. В результате многочисленных наблюдений и исследований установлены некоторые средние значения изменения с высотой температуры и давления воздуха, а следовательно, и его плотности, которые приняты в качестве стандартных. Соответствующие данные в виде таблицы стандартной атмосферы широко используются при аэродинамических расчетах, градуировке авиационных приборов и т. д.
Таблица стандартной атмосферы
| Бы- | Температура | Массовая плотность | Давление Р, кг-с2 | Относительное давле- | Относительная плот- | Скорое ка на высоте | гь зву-данной а |
| та | |||||||
| Я, и | t C | м4 | ние | ность | |||
| ха, ρ, кг/м2 | Р/Ро | ρ/ρо | м/с | ||||
| 15,00 | 0,1249 | 1,000 | 1,000 | 340,4 | |||
| 11,75 | 0.1190 | 0,942 | 0,953 | 338,5 | |||
| 8,50 | 0,1134 | 0,887 | 0,907 | 336,6 | |||
| 5,25 | 0,1079 | 0,835 | 0,864 | 334,6 | |||
| 2,00 | 0,1026 | 0,785 | 0,882 | 332,7 | |||
| —1,25 | 0,0976 | 0,737 | 0,781 | 330,7 | |||
| —4,50 | 0,0927 | 0,692 | 0,742 | 328,7 | |||
| —7,75 | 0,0880 | 0,649 | 0,705 | 326,7 | |||
| —11,00 | 628S | 0,0835 | 0,608 | 0,669 | 324,7 | ||
| — 14,25 | 0,0792 | 0,570 | 0,634 | 322,7 | |||
| — 17,50 | 0,0751 | 0,533 | 0,601 | 320,7 | |||
| —20,75 | 0,0711 | 0,498 | 0,569 | 318,6 |
| —24,00 | 0,0673 | 0,466 | 0,539 | 316,6 | |||
| —27, 25 | 0,0636 | 0,435 | 0,509 | 314,5 | |||
| —30,50 | 0,0601 | 0,405 | 0,481 | 312,4 | |||
| -33,75 | 0,0568 | 0,378 | 0,454 | 310,3 | |||
| 8ООО | —37,00 | 0,0536 | 0,351 | 0,429 | 308,2 | ||
| —40,25 | 0,0505 | 0,327 | 0,404 | 306,1 | |||
| —43,50 | 0,0476 | 0,303 | 0,381 | 303,9 | |||
| (1500 | —46,75 | 0,0448 | 0,282 | 0,358 | 301,8 | ||
| —50,00 | 0,0421 | 0,261 | 0,337 | 299,6 | |||
| —53,25 | 0,0395 | 0,242 | 0,317 | 297,4 | |||
| —56,50 | 0,0371 | 0,223 | 0,297 | 295,2 | |||
| —56,50 | 0,0343 | 0,206 | 0,275 | 295,2 | |||
| —56,50 | 0,0317 | 0,191 | 0,254 | 296,2 | |||
| —56,50 | 0,0293 | 0,176 | 0,235 | 295,2 | |||
| —56,50 | 0,0271 | 0,163 | 0,217 | 295,2 | |||
| —56,50 | 0,0250 | 0,151 | 0,200 | 295,2 1 | |||
| 14 ООО | —56,50 | 0,0231 | 0,139 | 0,185 | 295,2 . | ||
| 14 500 | —56,50 | 0,0214 | 0,129 | 0,171 | 295,2 | ||
| —56,50 | 0,0197 | 0,119 | 0,158 | 295,2 | |||
| . —56,50 | 0,0183 | 0,110 | 0,146 | 295,2 | |||
| —56,50 | 0,0169 | 0,102 | 0,135 | 295,2 . | |||
| —56,50 | 0,0156 | 0,094 | 0,125 | 295,2 | |||
| —56,50 | 0,0144 | 0,087 | 0,115 | 295,2 | |||
| —56,50 | 0,0133 | 0,080 | 0,107 | 295,2 | |||
| —56,50 | 0,0123 | 0,074 | 0,099 | 295,2 | |||
| ! 8500 | —56,50 | 0,0114 | 0,068 | 0,091 | 295,2 | ||
| —56,50 | 0,0105 | 0,063 | 0,084 | 295,2 | |||
| —56,50 | 0,0097 | 0,058 | 0,078 | 295,2 | |||
| —56,50 | 0,0097 | 0,054 | 0,072 | 295,2 | |||
| —56,50 | 0,0077 | 0,046 | 0,061 | 295,2 | |||
| —56,50 | 0,0065 | 0,039 | 0,052 | 295,2 | |||
| —56,50 | 0,0056 | 0,034 | 0,045 | 295,2 | |||
| —56,50 | 0,0048 | 0,029 | 0,038 | 295,2 | |||
| —56,50 | 0,0041 | 0,025 | 0,033 | 295,2 |
Как видно из таблицы, на уровне моря (или у поверхности земли) стандартными атмосферными условиями являются: температура t = + l5°С (Т=288 абс), барометрическое давление Р= 10332 кг/м2 и плотность воздуха ρ≈ 0,125 кг-с2/м4. В нижнем слое земной атмосферы—тропосфере, которая в стандартных условиях простирается, до высоты //=11 км, температура по мере подъема уменьшается па 6,5° С на каждый километр высоты. Выше, где начинается стратосфера, температура до высоты 25—30 ‘км считается постоянной . и равной —56,5° С. Стандартные характеристики атмосферы для больших высот в нашем случае не нужны. Но следует упомянуть, что согласно
данным исследований атмосферы с высоты 25—30 км температура начинает возрастать, достигая на высотах около 50 км величины, близкой к 0°С. Далее начинается новое понижение температуры, и на высоте 70—90 км она равна приблизительно —75° С. Выше 90 км температура опять начинает повышаться, становясь на высоте 200 км более +500° С.
Уменьшение плотности воздуха с высотой означает увеличение средней длины свободного пробега молекул, У земли эта длина составляет около 0,1 микрона, а на высоте 200 км выражается сотнями метров.
Если для высот, исчисляемых немногими десятками километров, длины свободного пробега молекул настолько малы, что можно рассматривать воздух как сплошную среду, то на высотах более 100 км эти длины становятся соизмеримыми с длиной летательного аппарата или даже могут быть значительно больше. В таких условиях воздушная среда практически состоит из свободных молекул, то есть таких, воздействие которых на летательный аппарат почти не связано с их взаимодействием между собой. Как показали теоретические исследования, некоторые особенности аэродинамики, связанные с увеличением длины свободного пробега молекул, могут проявляться уже при полетах на высотах более 40 км.
Г л а в а II.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
| Приложение Физические свойства сухого воздуха при рв – 760 мм рт. ст. Таблица 4.
Цель работы. Определение экспериментальным путем на виртуальной имитационной компьютерной модели лабораторной «установки» коэффициента теплоотдачи при свободной конвекции в неограниченном пространстве. Изучение методики обработки экспериментальных данных с применением теории подобия и составления критериального уравнения по результатам эксперимента. КРАТКИЕ СВЕДЕНИЯ Этот вид конвективного переноса теплоты играет преимущественную роль в процессах отопления жилых и производственных помещений и имеет значение в различных областях техники. Например, нагревание комнатного воздуха отопительными приборами, а также нагревание и охлаждение ограждающих конструкций помещений (стены, окна, двери и пр.) осуществляется в основном в условиях естественной конвекции или, так называемого, свободного потока. Естественная конвекция возникает в неравномерно нагретом газе или жидкости, находящихся в ограниченном или неограниченном пространстве, и может влиять на конвективный перенос теплоты в вынужденном потоке среды. В больших масштабах свободное перемещение масс подвижной среды (воздушных и водных масс), вызванное различием их плотностей в отдельных местах пространства, осуществляется в атмосфере земли, водных пространствах океанов и морей и т. д. К настоящему времени достаточно полно изучен естественный конвективный теплообмен для тел канонических форм (плита, цилиндр, шар), находящихся в различных подвижных средах, заполняющих пространство больших размеров по сравнению с размерами самого тела. Как показывает опыт, характер свободного течения среды относительно поверхности нагретого тела бывает как ламинарным, так частично или полностью турбулентным (ламинарный и турбулентный пограничные слои). теплоотдачи в условиях естественной конвекции у вертикального цилиндра большой высоты. На нижнем участке трубы наблюдается ламинарное течение воздуха вверх (ламинарный пограничный слой). На некотором расстоянии от нижнего конца трубы перемещение слоев воздуха теряет ламинарный характер, возникают отдельные локонообразные потоки массы, появляются искривленные струйки, которые далее дробятся на более мелкие, и восходящий поток воздуха у нагретой трубы приобретает турбулентный характер с ламинарным пристенным подслоем (турбулентный пограничный слой). Рис. 1 является хорошей иллюстрацией развития и перехода ламинарного пограничного слоя в турбулентный. Экспериментально коэффициент теплоотдачи может быть определен из основного уравнения теплоотдачи Ньютона-Рихмана 13. Ривкин С.Л. Термодинамические свойства газов. – М.: Энергоатомиздат, 1987. – 288 с. ОГЛАВЛЕНИЕ Схема и описание установки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 Расчетные формулы и расчеты . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 Порядок выполнения работы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .10 Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 Содержание отчета . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .14 Библиографический список . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .14 Приложение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .16 СОДЕРЖАНИЕ ОТЧЕТА 1. Формулировку цели работы. 2. Краткие теоретические сведения. 3. Принципиальную схему экспериментальной установки и ее описание. 4. Порядок выполнения работы. 5. Таблицы замеренных и вычисленных величин. 6. Количественное сравнение коэффициентов теплоотдачи, полученных экспериментальными и расчетным способами. 7. Выводы. Библиографический список 2. Мазур Л. Техническая термодинамика и теплотехника. – М.: ГЭОЭР-МЕД, 2003. -350 с. 3. Теория тепломассообмена. Учебник для технических университетов и вузов / С.И. Исаев, И.А. Кожинов, В.И. Кофанов и др.; Под ред. А.И. Леонтьева – 2-е изд., испр. и доп. – М.: Изд-во МГТУ им. Н.Э. Баумана, 1997. – 683 с. 4. Кудинов В.А., Карташов Э.М. Техническая термодинамика. – М.: Высшая школа, 2003. – 261 с. 5. Исаченко В.П., Осипова В.А., Сукомел А.С. Теплопередача. – М.: Энергоиздат, 1981. – 486 с. 6. Михеев М.А., Михеева И.М. Основы теплопередачи. – М.: Энергия, 1977. – 319 с. 7. Мухачев Г.А., Щукин В.К. Термодинамика и теплопередача. – М.: Высшая школа, 1991. – 479 с. 8. Нащокин В.В. Техническая термодинамика и теплопередача. М.: Высшая школа, 1980. – 261 с. 9. Осипова В.А. Экспериментальное исследование процессов теплообмена. – М.: Энергия, 1979. – 319 с. 10. Задачник по технической термодинамике и теории тепломасообмена / Под ред. В. Крутова, Г. Петражицкого. – М.: Высшая школа, 1986. – 383 с. 11. Краснощеков Е.А., Сукомел А.С. Задачник по теплопередаче. – М.: Энергия, 1980. – 288 с. откуда , (1) где – тепловой поток, передаваемый свободной конвекцией от поверхности твердого тела в подвижную окружающую среду; – теплоотдающая поверхность; – температурный напор между поверхностью тела и окружающей подвижной средой. Свободный конвективный теплообмен тел в средах, находящихся в неограниченном пространстве, экспериментально изучался различными исследователями. Опыты проводились с телами канонических форм (плиты, цилиндры, шары) с размерами от 15 мк (диаметры проволоки) и до 16 м (диаметры сфер шаров) в различных средах (различные газы и жидкости). Согласно теории подобия, результаты исследований обобщались с помощью характерных для этого явления критериев Nu, Gr и Рг. Результаты, полученные экспериментальным путем, находятся в полном соответствии и с аналитическими решениями этих задач. Влияние изменения физических параметров на теплообмен в пограничном слое удается учесть введением отношения критериев , представляющего относительное изменение параметров переноса (кинематическая вязкость ) и (температуропроводность) в пределах изменения температуры среды: − температура потока окружающей среды вдали от стенки, − температура среды на границе со стенкой. Академиком М. А. Михеевым, на основании обобщения результатов экспериментального исследования, рекомендуются следующие формулы для расчета средних коэффициентов теплоотдачи в свободном потоке. Для горизонтальных труб в диапазоне изменения числа () от 103до 108 , где − средний критерий Нуссельта, − критерий Грасгофа; − критерий Прандтля при температуре потока окружающей среды; − критерий Прандтля жидкости при температуре среды на границе со стенкой. Для вертикальных труб и плит в диапазоне изменения числа () от 103 до 109, что отвечает ламинарному течению среды около поверхности, , и в диапазоне изменения числа , что отвечает турбулентному течению около поверхности , где h – высота теплоотдающей поверхности. Для газов число мало зависит от температуры и его можно принять за 1. Для тонких проволок малого размера, для которых выполняется условие , критерий конвективного теплообмена имеет постоянное число . Это предельное наименьшее значение критерия Nu отвечают неподвижному пограничному слою, когда теплоотдачу можно вычислить непосредственно по формулам теплопроводности. Между этим предельным состоянием полностью заторможенной среды в пограничном слое и рассмотренным режимом свободной конвекции, при которой в пограничном слое осуществляется течение среды с участием инерционных сил и сил внутреннего вязкостного трения, существует режим свободной конвекции с ползущим течением в пограничном слое. |
zakon.znate.ru
Физические параметры сухого воздуха при 1 атм
Влажный газ является смесью сухого газа и водяного пара . В дальнейшем под влажным газом будет подразумеваться только влажный воздух, учитывая, что физические свойства топочных газов и влажного воздуха отличаются лишь количественно. Влажный воздух как влаго- и теплоноситель характеризуется следующими основными параметрами абсолютной и относительной влажностью, влагосодержанием и энтальпией (теплосодержанием). [c.584]ПРИЛОЖЕНИЕ 2 Физические параметры сухого воздуха при I атм [443] [c.617]
Физические параметры сухого воздуха при атмосферном давлении [c.447]
Физические параметры сухого воздуха [c.105]
ФИЗИЧЕСКИЕ ПАРАМЕТРЫ СУХОГО ВОЗДУХА ПРИ В = 760 мм. рт. ст [c.323]
Физические параметры сухого воздуха принимаются по табл. 6. Коэффициент теплопроводности воздуха А,=0,02715 ккал/м-час-град. [c.105]
Физические параметры сухого воздуха при постоянном давлении 980 гПа — см. также рис, 28, 29 [c.69]
Рг—критерий Прандтля, характеризующи физические параметры сухого газа или воздуха [c.250]
Физические параметры сухого воздуха при р = кГ/см [71] [c.716]
Физические параметры для сухого воздуха при Р-1 кг/сл [c.94]
Физические параметры сухого воздуха при В = 76Э мм рт. ст. [c.157]
Основные физические параметры сухого воздуха и воды приведены в приложении. [c.49]
Сухой воздух состоит в основном из азота и кислорода. В сухих топочных газах, полученных при полном сгорании топлива, содержится, кроме того, определенное количество двуокиси углерода, а также летучей золы. Из всех физических параметров сухого газа и воздуха различаться будут только величины плот- [c.11]
Физическое состояние атмосферного воздуха, или, как его чаще называют, влажного воздуха, характеризуется рядом параметров температурой по сухому термометру, относительной влажностью, влагосодержанием, барометрическим давлением, парциальным давлением водяных паров, энтальпией. [c.185]
В табл. А.З и А.4 приведены физические параметры воды на линии насыщения и сухого воздуха при давлении р=10 Па. [c.69]
www.chem21.info
Физические свойства воздуха – Энциклопедия по машиностроению XXL
При температуре набегающего потока /о=Ю°С физические свойства воздуха v= 14,16-10- м /с Л = 2,5Ы0-2 Вт/(м-°С). [c.62]Прн температуре набегающего потока о = 20°С физические свойства воздуха следующие [c.64]
При Jfi = 90 мм /, 11 = 20+14,9-90-С и при этой температуре физические свойства воздуха следующие [c.121]
При температуре /ж = 20° С физические свойства воздуха следующие v = 15,06-10-е mV X, = 2,59-10-2 Вт/(м.°С). [c.135]
Физические свойства воздуха при температуре /,, =20°С Уж = = 15,06-10- mV Я, = 2,59-10-2 Вт/(м-°С). [c.137]
При 1к=20°С физические свойства воздуха следующие [c.150]
При — 100° С физические свойства воздуха определяем по таблицам Приложения [c.229]
Физические свойства воздуха = 5,74-10 Вт/ [c.260]
Температура и давление окружающей среды равны —Зб С и 2530 Па соответственно. Физические свойства воздуха- [c.261]
Данные о физических свойствах воздуха [c.261]
Физические свойства воздуха при температуре 0,5 ([c.285]
Физические свойства воздуха берутся из таблиц Приложения, [c.337]
Значения физических свойств воздуха при fiK = 300° Хж=0,046 Вт/ м- С) и V =48,33-10- м /с [c.102]
Значения физических свойств воздуха при 7 = 300°С [c.109]
Физические свойства воздуха как рабочего тела [c.171]
Международная станда.рт-ная атмосфера — принятый закон изменения физических свойств воздуха с высотой, который близок к средним действительным закономерностям. Таким образом появляется возможность сравнения испытаний, проведённых в различных условиях. [c.387]
Уравнения (12-9) и (12-10) при этом упрощаются до обыкновенных дифференциальных уравнений. В расчетах использованы также следующие температурные зависимости физических свойств (аппроксимирующие изменение физических свойств воздуха в диапазоне температур от 300 до 1 300 °С) [c.321]
| Рис. А-1. Физические свойства воздуха при атмосферном давлении. | 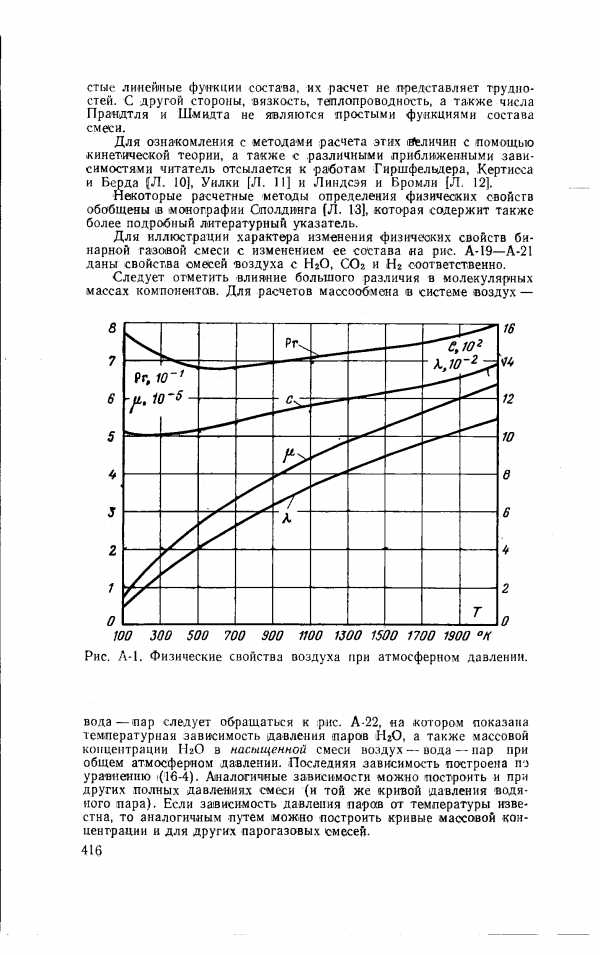 |
Скорости, при которых на физические свойства воздуха за скачком уплотнения начинает влиять возбуждение внутренних степеней свободы молекул воздуха, называются гиперзвуковыми скоростями. Так, например, гиперзвуковым называется снаряд, который летит со скоростью, превышающей число Маха, равное примерно 5. [c.461]
Физические свойства воздуха и дымовых газов (при среднем содержании по объему СОг ==13% Н20=11%) [c.349]
Все физические свойства воздуха берутся из таблицы, приводимой в приложении (см.. табл. П10) для определяющей температуры н,1==20°С 1=0,026 Вт/(м-К) Р1=1,205 кг/м Ц1=18,1 X [c.250]
Толщина гидродинамического пограничного слоя, как правило, мала по сравнению с расстоянием х. Например, для потока воздуха с дао=3 м/с и /о=20°С (температура набегающего потока, по которой из таблиц выбираются физические свойства воздуха р и .1) величина 6=10,4 мм при х=1 м. [c.253]
Решение. Определяющая температура равна 10 С. Физические свойства воздуха берем для этой температуры из табл. П10 р=1,247 кг/мЗ ц=17,6-10- Н-с/м Я,=0,0251 Вт/(м-К). [c.264]
Графики на рис, 9-5 иллюстрируют влияние переменных физических свойств воздуха на распределение по радиусу трубы температуры, скорости, массовой скорости и плотности теплового потока. Обращает [c.186]
По сравнению с гидравлическими пневматические приводы имеют большие скорости срабатывания и более простые конструкции. У пневматических приводов значительно короче возвратные линии к ним предъявляют меньшие требования в отношении герметичности. В силу особенностей физических свойств воздуха работа пневматической системы в меньшей степени зависит от колебаний температуры, чем у гидравлических систем. [c.21]
При очень высоких скоростях полета значительное повышение температуры за ударной волной изменяет физические свойства воздуха. В частности, он г ерестает быть прозрачным и поэтому становится источником радиационного теплового потока к поверхности. Непрозрачность воздуха обусловлена главным образом значительным повышением концентрации в нем окиси азота при высоких температурах. [c.702]
В термодинамическом цикле ГТУ с подводом теплоты при р = onst (рис. 11.7) известны следующие параметры = 17 °С pjpi — 3,5 1з = 650 °С. Определить удельные индикаторный и эффективный расходы топлива в установке, если теплотворная способность топлива Qp = = 41 ООО кДж/кг, расход воздуха = 5000 кг/ч, относительный индикаторный (внутренний) к. п. д. установки Tioi 0,73, механический к. п. д. т] = 0,88. При расчете пренебречь разницей в физических свойствах воздуха и продуктов сгорания топлива, а также количеством теплоты, [c.130]
Найти средний коэффициент теплоотдачи от воздушного потока к плоской пластине длиной I = 200 мм, обтекаемой в продольном направлении. Скорость потока 1000 м/с. Температура поверхности пластины 227° С. Статическое давление и температура потока равны 500 Па и —65° С. Физические свойства воздуха = 0,04 Вт/(м-К) М.т = 2,67.10- Па-с – 1,21-10-” Па-с Ргст -= 0,68. [c.256]
С и 32,2 кПа. Крыло обтекается под нулевым углом атаки. Режим течения в пограничном слое турбулентнь й. Физические свойства воздуха Х.ст=0,03 Вт/(м-К.) (Хст = = 2,07-10- Па-с РГст = 0,7. [c.257]
При расчете теплоотдачи учесть влияние на теплообмен продольного градиента давления, числа М , изменения температуры вдоль поверхности профиля, изменения физических свойств воздуха с температурой, а также основное влияние диссоциации. Считать, чтои изменяются с высотой в соответствии с таблицами международной стандартной атмосферы [171. [c.264]
Задача сводится к отысканию Сип (см. пример 2.6 из 2.3). Показатель степени п находится как тангенс угла наклона прямой линии, усредняющей опытные точки, нанесенные на график с логарифмическими координатами. Значение С определяется по значениям Ыпоо и Ре в какой-либо произвольной точке, принадлежащей прямой. Пр и вычислении чисел подобия физические свойства воздуха. следует выбирать по среднеарифметической температуре, равной 0,5(г ж1+ 2). [c.170]
Наиболее широко применяется карта режимов для го ризонтального течения Бейкера [5.5]. Для определения границ областей режимов им введены параметры, которые включают физические свойства. Диаграмма Бейкера, представленная на рис. 5.1, построена в координатах (без учета постоянных коэффициентов) 4,882GJ p/A, — ЯгрСпр/0″р, в которых G”p и Gjjp — массовые скорости соответственно жидкой и газообразных фаз, кг/м -час, а параметры Я, и i ) — нормирующие коэффициенты для физических свойств фаз, определяемые отношением физических свойств фаз данной системы к физическим свойствам воздуха (Л) и воды (IF), при нормальных условиях [c.121]
Физические свойства воздуха выбирайте при температуре 260 С и считайте 1постоя1тыми. [c.181]
К сожалению, опытные данные, которые позволили бы разрешить это противоречие, отсутствуют. Если провести тот же расчет по методу определяющей температуры, предложенному Эккертом, то при использовании физических свойств воздуха при умеренных температурах получим п = —0,19, т = —0,27. Однако метод расчета Эккерта не имеет достаточного физического обоснования. Поэтому можно сделать лишь тот вывод, что при То1Тос1 отсутствуют как опытные данные, так и аналитические расчеты. Однако некоторые выводы можно сделать на основании косвенных данных. Согласно большинству опытных данных для турбулентного течения в трубах наиболее вероятное значение п = —0,5. Трудно представить себе, что соответствующее значение п для турбулентного внешнего пограничного слоя значительно отличается от этой величины. Кроме того, в следующей главе будет показано, что число Маха влияет на теплообмен и сопротивление через изменение физических свойств с температурой. Согласно аналитическим и экспериментальным данным для турбулентных высокоскоростных потоков значения лит лежат в диапазоне от —0,5 до —0,6. [c.324]
Сравиите схемы расчета коэффициентов теплоотдачи и трения для ламинарного иолраничного слоя с постоянной скоростью на внешней границе при нагревании и охлаждении по определяющей температуре и по фактору свойства , используя табличные зяаче-ния физических свойств воздуха. [c.326]
Топки с кипящим слоем. В кипящем слое частицы мелкозернистого материала под действием аэродинамических сил потока воздуха переходят в подвижное состояние и еовершают беспорядочное циркуляционное движение в некотором объеме над колосниковой решеткой [Л. 17]. Скорость воздуха в межкусковых каналах слоя, при которой начинается кипение , называется критической скоростью слоя (Шкр)- Она определяется размером, формой и плотностью частиц, а также физическими свойствами воздуха (газа). Чем выше скорость потока сверх критической, тем больше разбухает слой (т. е. увеличивается по высоте). Устойчивое состояние его наблюдается до определенной скорости, называемой предельной (Шкр), при которой все частицы материала уносятся потоком. [c.38]
Важнейшей особенностью характеристик компрессора является их зависимость от параметров и физических свойств воздуха. Изменение его температуры вызывает изменение плотности и, следовательно, массового расхода. В меньшей мере на плотность воздуха влияет изменение его давления и влажности. Происходят также изменения числа Маха и показателя изоэнтро-пы, что влечет за собой изменение характеристик компрессора. Следует помнить, что рабочим телом в компрессоре энергетической ГТУ является забираемый из атмосферы воздух, поэтому установка реагирует на изменения параметров воздуха. [c.51]
Все физические свойства воздуха и Ср, Л, р, X до 700° К и ц до 1 100° К для водорода были приняты по данным [Л. 5]. Значения X для водорода при Т от 1 200 до 2 000° К рассчитывались по эмпирическому уравнению, предложенному в (Л. 6], а при Т от ТОО до 1 200° К находились путем графической интерполяции. Значения ц для водорода при Г=1 100-7-2 000° К были рассчитаны теоретически с использованием модифицированного потенциала Букингема. [c.186]
mash-xxl.info
Плотность сухого воздуха – Энциклопедия по машиностроению XXL
Поскольку масса влажного воздуха состоит из массы сухой его части Ш(. и массы водяных паров т , то плотность воздуха рассматривается как сумма плотностей сухого воздуха (рс) и водяного пара (р ) [c.145]Первое слагаемое выражения (15.18) представляет собой плотность сухого воздуха при барометрическом давлении (р = = 1,276 кг/м при Ро = 1000 гПа = 750 мм рт. ст.). [c.145]
Состояние атмосферного воздуха определяется следующими параметрами барометрическим давлением р = = 10 Па, температурой t= 15 °С, парциальным давлением водяного пара по психрометру = 1 70 Па. Определить относительную влажность ср абсолютную влажность р плотность сухого воздуха плотность смеси пара и воздуха р температуру точки росы газовую постоянную влажного воздуха R влагосодержание воздуха d и энтальпию воздуха i. [c.68]
Па (кгс/м ), определяют по средней для данного участка скорости потока и температуре и по плотности сухого воздуха при давлении в 0,1 МПа (760 мм рт. ст.), а в конце расчета вводят поправку на действительную плотность дымовых газов. Скорости потока и температуры (средние) принимают из теплового расчета. [c.346]
В связи с этим порядок расчета газового тракта таков. Сначала рассчитываются все сопротивления по плотности сухого воздуха, затем рассчитывается самотяга по отдельным участкам тракта. Сопротивления суммируются с внесением всех необходимых поправок, отдельно суммируется самотяга, обычно без поправок, и, наконец, по величине алгебраической разности сопротивлений и само-тяги определяется перепад полных давлений [c.24]
Для парогазовой смеси, когда подъемная сила определяется не только разностью температур, но и разностью влагосодержаний (плотность влажного воздуха меньше, чем плотность сухого воздуха), критерий Ог должен быть заменен критерием Ат. [c.107]
Решение. Дано ) + D( = 0,0445 ж >=0,0383 м. Плотность сухого воздуха принимаем равной 1,024 к.г1м . [c.289]
Массовый и объемный состав сухого воздуха приведен в табл. 8. Плотность сухого воздуха при нормальных физических условиях (0° С и 760 мм рт. ст., или примерно 1,01 бар) равна 1,293 [c.60]
Плотность сухого воздуха при нормальных условиях Р = 0,001293 г смК [c.570]
Плотность сухого воздуха Pj.g и его удельный объём можно определить из уравнения Клапейрона Рс.в Рс в/(- с в с в) с.в — VP .b [c.37]
В табл. 2.3 приведены значения плотности сухого воздуха для различных значений температур и давлений, вычисленные по уравнению Клапейрона. [c.37]
Плотность сухого воздуха [c.37]
Плотность сухого воздуха в помещении [c.43]
Пример 4.1. Влажный воздух массой твл.в = 3,2 кг содержит влагу массой вл = 0,1 кг. Определить массовую концентрацию влагосодержание d, массу сухого воздуха тпс , плотность влажного воздуха Рвл.в и его удельные объёмы Увл.в и V. Плотность сухого воздуха рс.в =1,128 кг/м . [c.79]
Перепады давлений рассчитывают по плотности сухого воздуха при нормальных условиях и по скорости газов или воздуха при этих же условиях. В конце расчета необходимо внести поправки на разницу плотностей газов и воздуха по отношению к принятой (нормальной) на запыленность и отличие среднего эффективного давления в тракте от ранее принятого. [c.87]
Плотность сухого воздуха при тех же давлении и температуре [c.269]
Ус — плотность сухого воздуха [c.56]
Из уравнения (39) видно, что при равном общем давлении и температуре плотность влажного воздуха ув ниже плотности сухого воздуха ус. [c.56]
Плотность влажного воздуха р складывается из плотностей сухого воздуха Ре и пара р или р”, т. е. [c.79]
При известных значениях температуры воздуха и парциального давления пара р определяется по таблицам перегретого водяного пара, ар” — по таблицам насыщенного пара. Если при этом известно давление влажного воздуха, то парциальное давление сухого воздуха рд также известно, и тогда плотность сухого воздуха определяется или по таблицам для воздуха, или по уравнению состояния идеального газа. [c.79]
Если известны температура, давление и относительная влажность воздуха, то плотность влажного воздуха может быть определена следующим образом. Плотность сухого воздуха [c.79]
Рн° = 22° 22 4 плотность сухого воздуха [c.37]
Влагосодержание. Влагосодержанием й влажного воздуха называется отношение массы водяного пара /Пп, содержащегося в смеси, к массе сухого воздуха Шв или, что то же, отношение плотности водяного пара Рп к плотности сухого воздуха рв, взятых при их парциальных давлениях и при температуре влажного воздуха [c.165]
Плотность сухого воздуха при нормальных условиях равна 1,293 кг/мз. При давлении Р, мм рт. ст., и температуре Т, °С, плотность воздуха может быть рассчитана по формуле [c.312]
Ув— плотность сухого воздуха 7в 1,29 кг/м — теплоемкость воздуха при постоянном [c.343]
Плотность сухого воздуха о, кг/деЗ [c.123]
Экспериментальным путем найдено ), что при 0° С и давлении, создаваемом (в Париже) 760 мм Hg при 0°С, плотность сухого воздуха равна 0,0012933 г см- . Если мы примем плотность ртути при 0° равной 13,5953 2) и 980,939, то мы имеем в абсолютных единицах [c.28]
Весовая плотность сухого воздуха при стандартном давлении и температуре равна 1,2255 кт/лг , а это означает, что 1 л воздуха при этих условиях весит 1,2255 кг. [c.9]
На графике (рис. 3) представлено изменение плотности сухого воздуха в зависимости от давления и температуры. [c.9]
Плотность сухого воздуха при различной темпера- [c.179]
Влажный воздух при данном давлении и температуре может содержать разное количество водяного пара. Смесь, состоящую из сухого воздуха и насыщенного водяного пара, называют насыщенным влажным воздухом. Парциальное давление водяного пара в этой смеси равно давлению насыщения при данной температуре. Количество пара в каждом кубическом метре такого воздуха численно равно плотности сухого насыщенного пара р” кг/м ). [c.236]
Масса пара в 1 м влажного воздуха, численно равная плотности пара Рп при парциальном давлении ри, называется абсолютной влажностью. Если при постоянной температуре t увеличивать влажность воздуха, то плотность водяного пара будет возрастать. Если же температура влажного воздуха будет ниже температуры насыщения водяного пара при давлении смеси, то предельной плотностью водяного пара будет плотность сухого насыщенного пара при парциальном давлении его, меньшем, чем давление смеси. В этом предельном состоянии влажный воздух будет представлять собой смесь сухого воздуха и сухого насыщенного водяного пара. [c.236]
Влажный воздух, который не содержит при данном давлении и температуре максимально возможное количество водяного пара, называют ненасыщенным. Ненасыщенный влажный воздух представляет собой смесь сухого воздуха и перегретого пара, что видно из ри-диаграммы (см. рис. 15-1). Парциальное давление перегретого пара в смеси будет меньше давления насыщения при данной температуре. Количество перегретого пара в 1 воздуха численно равно плотности перегретого пара, но меньше численной величины плотности сухого насыщенного пара. Охлаждая воздух, а следовательно, и перегретый пар при каком-либо постоянном давлении р, например, по линии 7-8, можно довести перегретый пар до состояния насыщения, характеризуемой точкой 8. Это будет тогда, когда температура воздуха станет равной температуре насыщения при данном парциальном давлении водяного пара. Эту температуру называют температурой точки росы. [c.238]
Плотность влажного воздуха равна сумме плотностей пара и сухого воздуха, взятых при своем парциальном давлении и при температуре смеси [c.240]
В интервале температур кондиционирования воздуха разница в плотностях влажного воздуха и сухой его части незначительна и можно считать л р . [c.48]
Относительной влажностью воздуха плотности водяного пара при его парциальном давлении и температуре смеси к плотности сухого насыщенного пара при той же температуре [c.90]
Максимально возможное содержание водяного пара в воздухе при температуре 1 будет в том случае, когда парциальное давление пара рп равно рп.и (точка 2). Очевидно, оно будет равно плотности сухого насыщенного пара р”=1/о” с давлением Рп.н и температурой fi. В этом случае влажный воздух представляет собой смесь воздуха и сухого насыщенного пара. Такой воздух называется насыщенным. С повышением температуры насыщенного влажного воздуха парциальное давление пара в нем возрастает, и при 1п р) состояние насыщения достигается в том случае, если сухого воздуха в смеси не будет вообще. Например, влажный воздух, находящийся при давлении ро = 0,1 МПа и температуре л 100°С, при любом парциальном давлении пара ри[c.152]
Значения плотности сухого воздуха, кг/м , в зависимости от давления Р) и темпера1уры (г) [c.82]
Плотность сухого воздуха при нормальных крмединамических условиях равна 1,293 кг/м . При,давлении р, Па, и температуре Т, К, плот-Ho f (в кг/м”) воздуха [c.16]
Плотность, газовая постоянная и средняя молекулярная масса влажного воздуха. Для решения различных инженерных задач часто нёобходимо внать плотность р влажного воздуха, которая равна сумме плотностей сухого воздуха ри и водяного пара р [c.337]
Плотность сухого воздуха при 760 мм рт. ст. и 0°С 1,293 кг1м = 1,293 г/дм . Плотность ртути при 0 С 13,59509 кг дм . [c.449]
Отметим теперь, что О- Величина ВК11 ) равна плотности сухого воздуха при барометрическом давлении. Тогда из формулы (1.46) следует вывод плотность влажного воздуха меньще, чем плотность сухого воздуха при том же (обычно барометрическом) давлении. Правда, разница плотностей невелика, поэтому в технических расчетах обьино принимают р Б = Рсв, хотя при необходимости более точные расчеты можно выполнять с использованием формулы (1.46). [c.35]
Задача 1.57. Определить массу продуктов сгорания, получаемых при полном сгорании 1 м природного газа Ставропольского месторождения состава С02 = 0,2% СН4 = 98,2% С2Нб = 0,4% СзН8 = 0,1% С4Ню = 0,1% N2=1,0%, если известно, что плотность сухого газа р = 0,728 кг/м . Коэффициент избытка воздуха в топке 0 = 1,15. [c.26]
mash-xxl.info