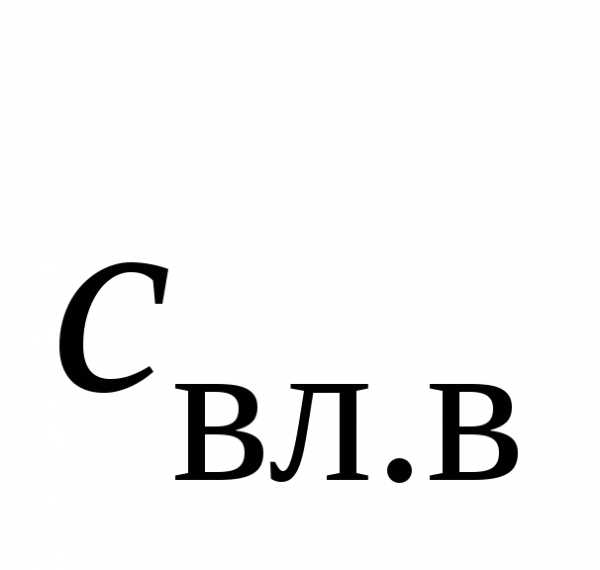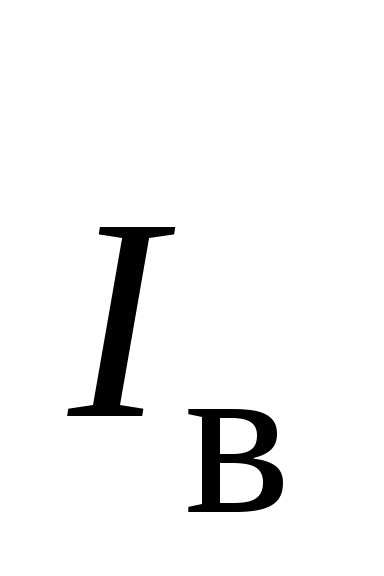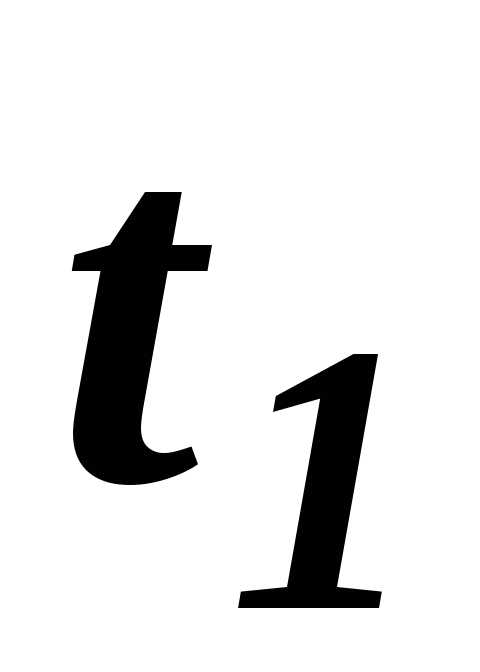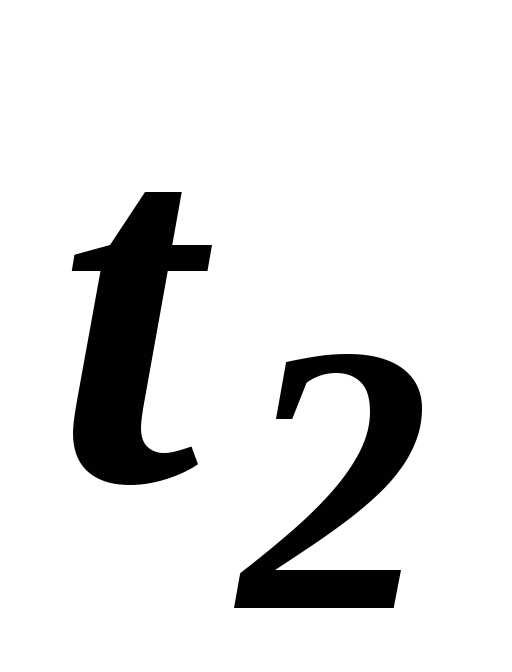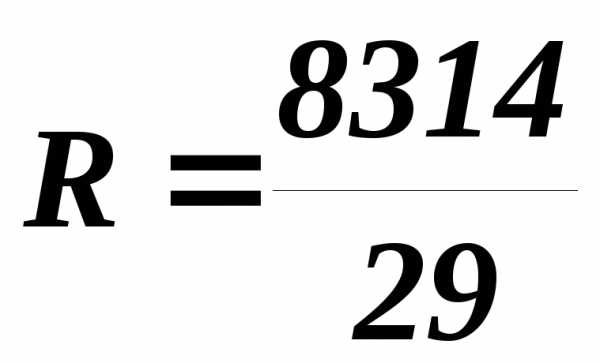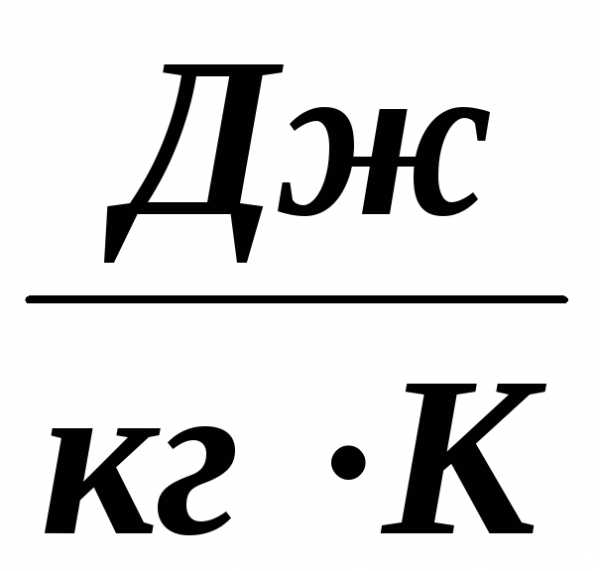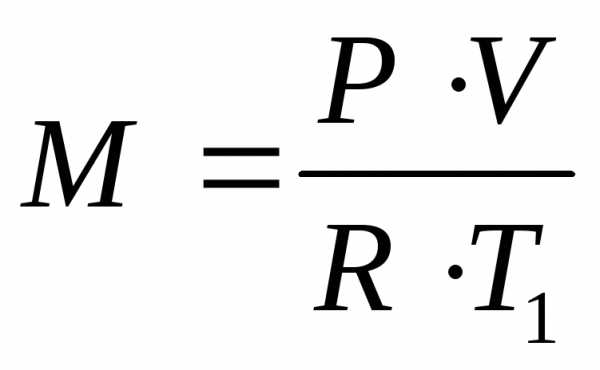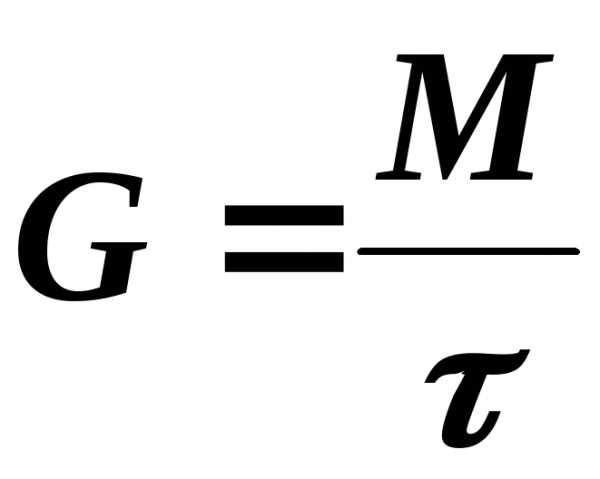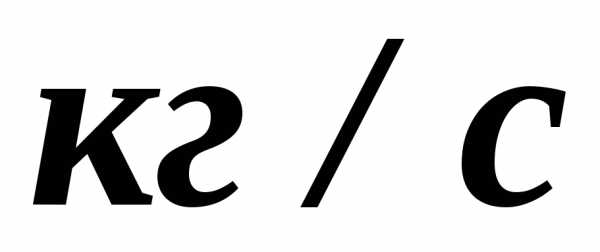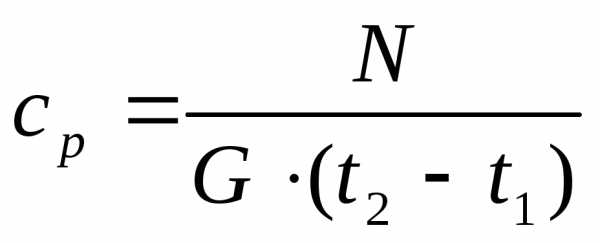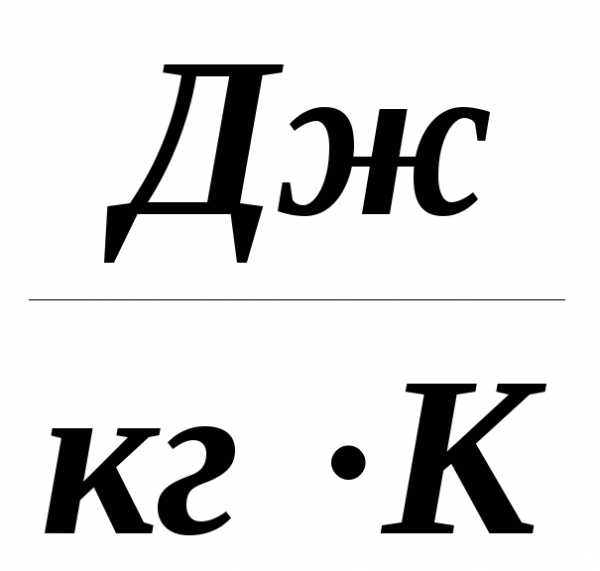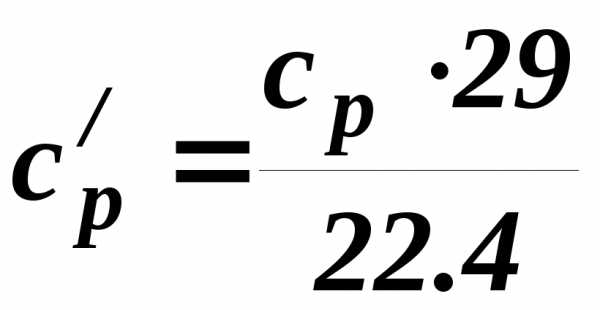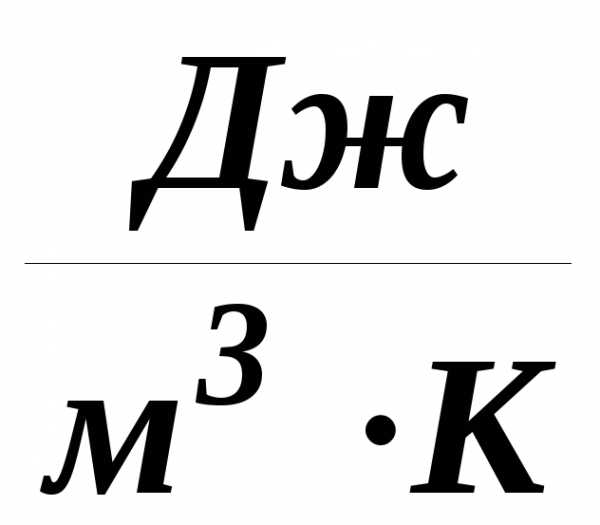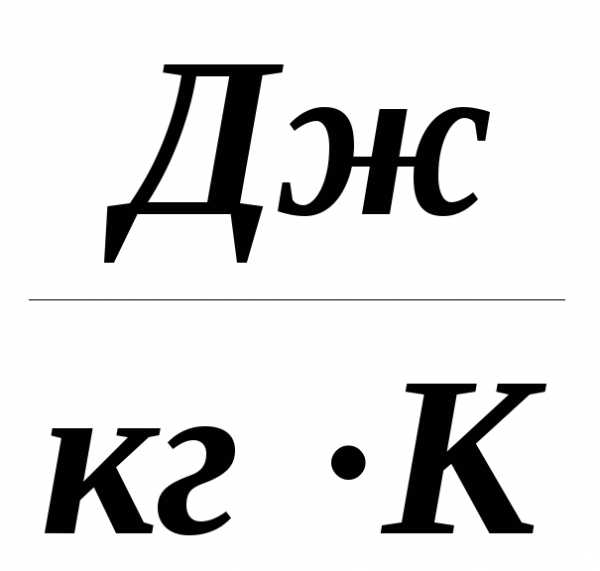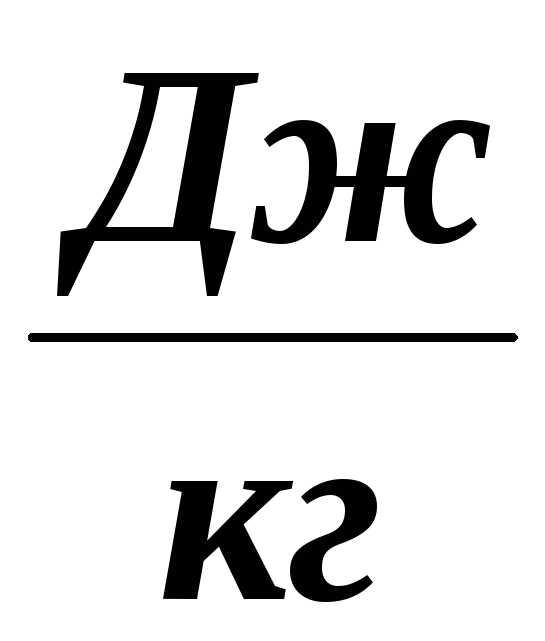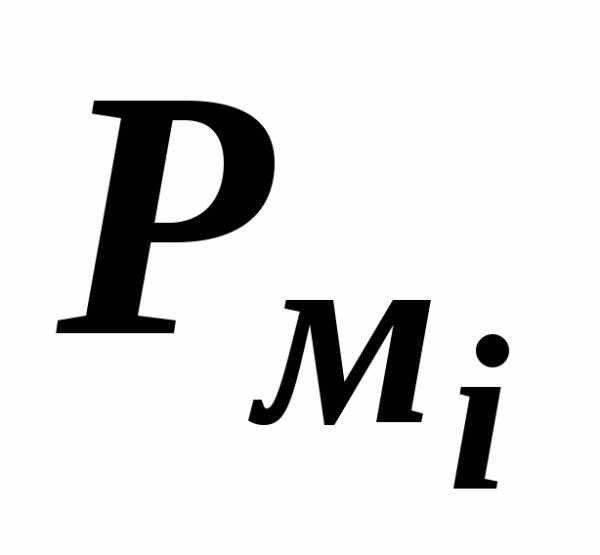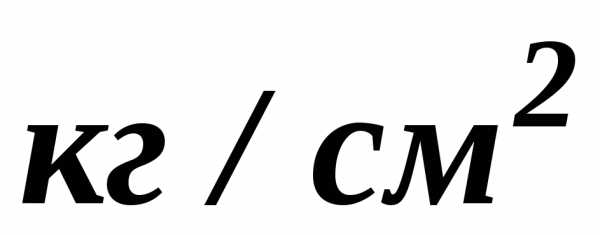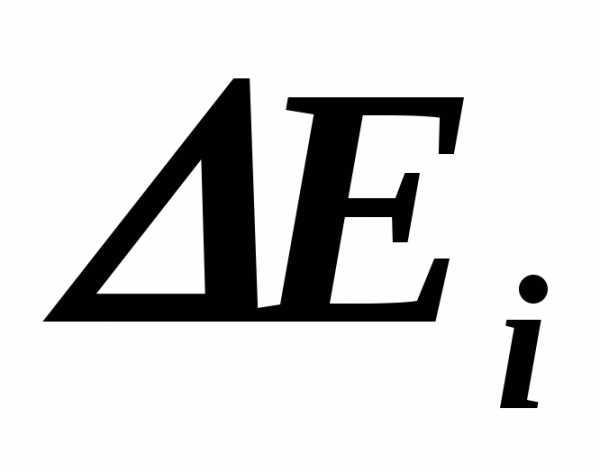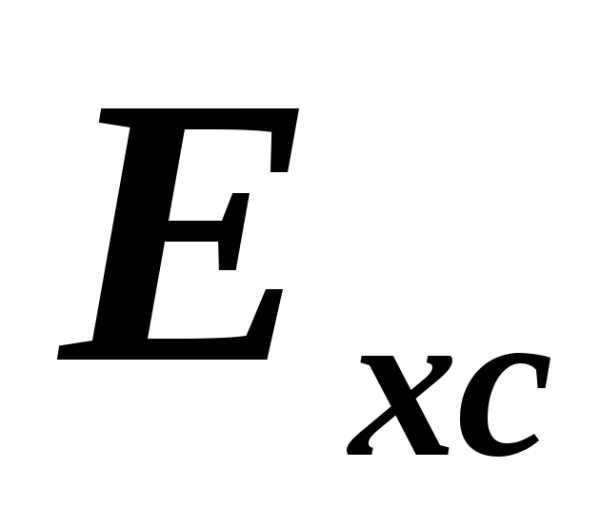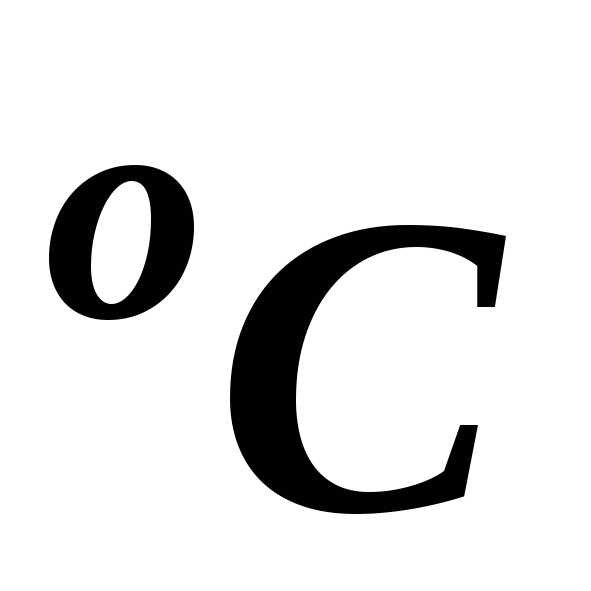Плотность воздуха, его удельная теплоемкость, вязкость и другие физические свойства: таблицы при различных температурах
Рассмотрены основные физические свойства воздуха: плотность воздуха, его динамическая и кинематическая вязкость, удельная теплоемкость, теплопроводность, температуропроводность, число Прандтля и энтропия. Свойства воздуха даны в таблицах в зависимости от температуры при нормальном атмосферном давлении.
Плотность воздуха в зависимости от температуры
Представлена подробная таблица значений плотности воздуха в сухом состоянии при различных температурах и нормальном атмосферном давлении. Чему равна плотность воздуха? Аналитически определить плотность воздуха можно, если разделить его массу на объем, который он занимает при заданных условиях (давление, температура и влажность). Также можно вычислить его плотность по формуле уравнения состояния идеального газа. Для этого необходимо знать абсолютное давление и температуру воздуха, а также его газовую постоянную и молярный объем. Это уравнение позволяет вычислить плотность воздуха в сухом состоянии.
На практике, чтобы узнать какова плотность воздуха при различных температурах
| t, °С | ρ, кг/м3 | t, °С | ρ, кг/м3 | t, °С | ρ, кг/м3 | t, °С | ρ, кг/м3 |
|---|---|---|---|---|---|---|---|
| -50 | 1,584 | 20 | 1,205 | 150 | 0,835 | 600 | 0,404 |
| -45 | 1,549 | 30 | 1,165 | 160 | 0,815 | 650 | 0,383 |
| -40 | 1,515 | 40 | 1,128 | 170 | 0,797 | 700 | 0,362 |
| -35 | 1,484 | 50 | 1,093 | 180 | 0,779 | 750 | 0,346 |
| -30 | 1,453 | 60 | 1,06 | 190 | 0,763 | 800 | 0,329 |
| -25 | 1,424 | 70 | 1,029 | 200 | 0,746 | 850 | 0,315 |
| -20 | 1,395 | 80 | 1 | 250 | 0,674 | 900 | 0,301 |
| -15 | 1,369 | 90 | 0,972 | 300 | 0,615 | 950 | 0,289 |
| -10 | 1,342 | 100 | 0,946 | 350 | 0,566 | 1000 | 0,277 |
| -5 | 1,318 | 110 | 0,922 | 400 | 0,524 | 1050 | 0,267 |
| 0 | 1,293 | 120 | 0,898 | 450 | 0,49 | 1100 | 0,257 |
| 10 | 1,247 | 130 | 0,876 | 500 | 0,456 | 1150 | 0,248 |
| 15 | 1,226 | 140 | 0,854 | 550 | 0,43 | 1200 | 0,239 |
При 25°С воздух имеет плотность 1,185 кг/м3. При нагревании плотность воздуха снижается — воздух расширяется (его удельный объем увеличивается). С ростом температуры, например до 1200°С, достигается очень низкая плотность воздуха, равная 0,239 кг/м3, что в 5 раз меньше ее значения при комнатной температуре. В общем случае, снижение плотности газов при нагреве позволяет проходить такому процессу, как естественная конвекция и применяется, например, в воздухоплавании.
Если сравнить плотность воздуха относительно плотности воды, то воздух легче на три порядка — при температуре 4°С плотность воды равна 1000 кг/м 3, а плотность воздуха составляет 1,27 кг/м3. Необходимо также отметить значение плотности воздуха при нормальных условиях. Нормальными условиями для газов являются такие, при которых их температура равна 0°С, а давление равно нормальному атмосферному. Таким образом, согласно таблице, плотность воздуха при нормальных условиях (при НУ) равна 1,293 кг/м3.
Динамическая и кинематическая вязкость воздуха при различных температурах
При выполнении тепловых расчетов необходимо знать значение вязкости воздуха (коэффициента вязкости) при различной температуре. Эта величина требуется для вычисления числа Рейнольдса, Грасгофа, Релея, значения которых определяют режим течения этого газа. В таблице даны значения коэффициентов динамической μ и кинематической ν вязкости воздуха в диапазоне температуры от -50 до 1200°С при атмосферном давлении.
Коэффициент вязкости воздуха с ростом его температуры значительно увеличивается.
При нагревании воздуха увеличиваются значения как кинематической, так и динамической вязкости. Эти две величины связаны между собой через величину плотности воздуха, значение которой уменьшается при нагревании этого газа. Увеличение кинематической и динамической вязкости воздуха (как и других газов) при нагреве связано с более интенсивным колебанием молекул воздуха вокруг их равновесного состояния (согласно МКТ).
| t, °С | μ·106, Па·с | ν·106, м2/с | t, °С | μ·106, Па·с | ν·106, м2/с | t, °С | μ·106, Па·с | ν·106, м2/с |
|---|---|---|---|---|---|---|---|---|
| -50 | 14,6 | 9,23 | 70 | 20,6 | 20,02 | 350 | 31,4 | 55,46 |
| -45 | 14,9 | 9,64 | 80 | 21,1 | 21,09 | 400 | 33 | 63,09 |
| -40 | 15,2 | 10,04 | 90 | 21,5 | 22,1 | 450 | 34,6 | 69,28 |
| -35 | 15,5 | 10,42 | 100 | 21,9 | 23,13 | 500 | 36,2 | 79,38 |
| -30 | 15,7 | 10,8 | 110 | 22,4 | 24,3 | 550 | 37,7 | 88,14 |
| -25 | 16 | 11,21 | 120 | 22,8 | 25,45 | 600 | 39,1 | 96,89 |
| -20 | 16,2 | 130 | 23,3 | 26,63 | 650 | 40,5 | 106,15 | |
| -15 | 16,5 | 12,02 | 140 | 23,7 | 27,8 | 700 | 41,8 | 115,4 |
| -10 | 16,7 | 12,43 | 150 | 24,1 | 28,95 | 750 | 43,1 | 125,1 |
| -5 | 17 | 12,86 | 160 | 24,5 | 30,09 | 800 | 44,3 | 134,8 |
| 0 | 17,2 | 13,28 | 170 | 24,9 | 31,29 | 850 | 45,5 | 145 |
| 10 | 17,6 | 14,16 | 180 | 25,3 | 32,49 | 900 | 46,7 | 155,1 |
| 15 | 17,9 | 14,61 | 190 | 25,7 | 33,67 | 950 | 47,9 | 166,1 |
| 20 | 18,1 | 15,06 | 200 | 26 | 34,85 | 1000 | 49 | 177,1 |
| 30 | 18,6 | 16 | 225 | 26,7 | 37,73 | 1050 | 50,1 | 188,2 |
| 40 | 19,1 | 16,96 | 250 | 27,4 | 40,61 | 1100 | 51,2 | 199,3 |
| 50 | 19,6 | 17,95 | 300 | 29,7 | 48,33 | 1150 | 52,4 | 216,5 |
| 60 | 20,1 | 18,97 | 325 | 30,6 | 51,9 | 1200 | 53,5 | 233,7 |
Примечание: Будьте внимательны! Вязкость воздуха дана в степени 106.
Удельная теплоемкость воздуха при температуре от -50 до 1200°С
Представлена таблица удельной теплоемкости воздуха при различных температурах. Теплоемкость в таблице дана при постоянном давлении (изобарная теплоемкость воздуха) в интервале температуры от минус 50 до 1200°С для воздуха в сухом состоянии. Чему равна удельная теплоемкость воздуха? Величина удельной теплоемкости определяет количество тепла, которое необходимо подвести к одному килограмму воздуха при постоянном давлении для увеличения его температуры на 1 градус. Например, при 20°С для нагревания 1 кг этого газа на 1°С в изобарном процессе, требуется подвести 1005 Дж тепла.
Удельная теплоемкость воздуха увеличивается с ростом его температуры. Однако, зависимость массовой теплоемкости воздуха от температуры не линейная. В интервале от -50 до 120°С ее величина практически не меняется — в этих условиях средняя теплоемкость воздуха равна 1010 Дж/(кг·град). По данным таблицы видно, что значительное влияние температура начинает оказывать со значения 130°С. Однако, температура воздуха влияет на его удельную теплоемкость намного слабее, чем на вязкость. Так, при нагреве с 0 до 1200°С теплоемкость воздуха увеличивается лишь в 1,2 раза – с 1005 до 1210 Дж/(кг·град).
Следует отметить, что теплоемкость влажного воздуха выше, чем сухого. Если сравнить теплоемкость воды и воздуха, то очевидно, что вода обладает более высоким ее значением и содержание воды в воздухе приводит к увеличению удельной теплоемкости.| t, °С | Cp, Дж/(кг·град) | t, °С | Cp, Дж/(кг·град) | t, °С | Cp, Дж/(кг·град) | t, °С | Cp, Дж/(кг·град) |
|---|---|---|---|---|---|---|---|
| -50 | 1013 | 20 | 1005 | 150 | 1015 | 600 | 1114 |
| -45 | 1013 | 30 | 1005 | 160 | 1017 | 650 | 1125 |
| -40 | 1013 | 40 | 1005 | 170 | 1020 | 700 | 1135 |
| -35 | 1013 | 50 | 1005 | 180 | 1022 | 1146 | |
| -30 | 1013 | 60 | 1005 | 190 | 1024 | 800 | 1156 |
| -25 | 1011 | 70 | 1009 | 200 | 1026 | 850 | 1164 |
| -20 | 1009 | 80 | 1009 | 250 | 1037 | 900 | 1172 |
| -15 | 1009 | 90 | 1009 | 300 | 1047 | 950 | 1179 |
| -10 | 1009 | 100 | 1009 | 350 | 1058 | 1000 | 1185 |
| -5 | 1007 | 110 | 1009 | 400 | 1068 | 1050 | 1191 |
| 0 | 1005 | 120 | 1009 | 450 | 1081 | 1100 | 1197 |
| 10 | 1005 | 130 | 1011 | 500 | 1093 | 1150 | 1204 |
| 15 | 1005 | 140 | 1013 | 550 | 1104 | 1200 | 1210 |
Теплопроводность, температуропроводность, число Прандтля воздуха
В таблице представлены такие физические свойства атмосферного воздуха, как теплопроводность, температуропроводность и его число Прандтля в зависимости от температуры. Теплофизические свойства воздуха даны в интервале от -50 до 1200°С для сухого воздуха. По данным таблицы видно, что указанные свойства воздуха существенно зависят от температуры и температурная зависимость рассмотренных свойств этого газа различна.
Теплопроводность воздуха λ при повышении температуры увеличивается во всем диапазоне, достигая при 1200°С величины 0,0915 Вт/(м·град). Другие теплофизические свойства воздуха такие, как его температуропроводность a и число Прандтля Pr, по-разному реагируют на изменение температуры. Температуропроводность, как и вязкость воздуха сильно зависит от температуры и при нагревании, например с 0 до 1200°С, ее значение увеличивается почти в 17 раз.
Число Прандтля воздуха слабо зависит от температуры и при нагревании этого газа его величина сначала снижается до величины 0,674, а затем начинает расти, и при температуре 1200°С достигает значения 0,724.
| t, °С | λ·102, Вт/(м·град) | а·106, м2/с | Pr | t, °С | λ·102, Вт/(м·град) | а·106, м2/с | Pr |
|---|---|---|---|---|---|---|---|
| -50 | 2,04 | 12,7 | 0,728 | 170 | 3,71 | 45,7 | 0,682 |
| -40 | 2,12 | 13,8 | 0,728 | 180 | 3,78 | 47,5 | 0,681 |
| -30 | 2,2 | 14,9 | 0,723 | 190 | 3,86 | 49,5 | 0,681 |
| -20 | 2,28 | 16,2 | 0,716 | 200 | 3,93 | 51,4 | 0,68 |
| -10 | 2,36 | 17,4 | 0,712 | 250 | 4,27 | 61 | 0,677 |
| 0 | 2,44 | 18,8 | 0,707 | 300 | 4,6 | 71,6 | 0,674 |
| 10 | 2,51 | 20 | 0,705 | 350 | 4,91 | 81,9 | 0,676 |
| 20 | 2,59 | 21,4 | 0,703 | 400 | 5,21 | 93,1 | 0,678 |
| 30 | 2,67 | 22,9 | 0,701 | 450 | 5,48 | 104,2 | 0,683 |
| 40 | 2,76 | 24,3 | 0,699 | 500 | 5,74 | 115,3 | 0,687 |
| 50 | 2,83 | 25,7 | 0,698 | 550 | 5,98 | 126,8 | 0,693 |
| 60 | 2,9 | 27,2 | 0,696 | 600 | 6,22 | 138,3 | 0,699 |
| 70 | 2,96 | 28,6 | 0,694 | 650 | 6,47 | 150,9 | 0,703 |
| 80 | 3,05 | 30,2 | 0,692 | 700 | 6,71 | 163,4 | 0,706 |
| 90 | 3,13 | 31,9 | 0,69 | 750 | 6,95 | 176,1 | 0,71 |
| 100 | 3,21 | 33,6 | 0,688 | 800 | 7,18 | 188,8 | 0,713 |
| 110 | 3,28 | 35,2 | 0,687 | 850 | 7,41 | 202,5 | 0,715 |
| 120 | 3,34 | 36,8 | 0,686 | 900 | 7,63 | 216,2 | 0,717 |
| 130 | 3,42 | 38,6 | 0,685 | 950 | 7,85 | 231,1 | 0,718 |
| 140 | 3,49 | 40,3 | 0,684 | 1000 | 8,07 | 245,9 | 0,719 |
| 150 | 3,57 | 42,1 | 0,683 | 1100 | 8,5 | 276,2 | 0,722 |
| 160 | 3,64 | 43,9 | 0,682 | 1200 | 9,15 | 316,5 | 0,724 |
Будьте внимательны! Теплопроводность воздуха в таблице указана в степени 102. Не забудьте разделить на 100! Температуропроводность воздуха указана в степени 106. Допускается интерполяция значений физических свойств воздуха в приведенных таблицах.
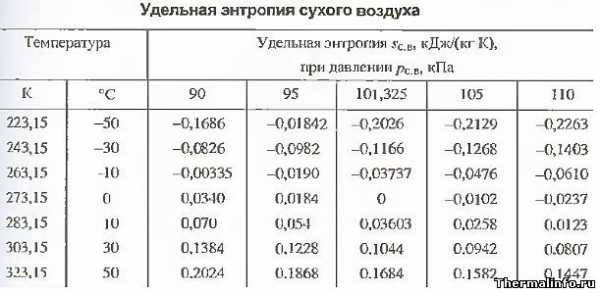
Энтропия сухого воздуха
В таблице представлены значения такого теплофизического свойства воздуха, как удельная энтропия. Значения энтропии даны для сухого воздуха в размерности кДж/(кг·град) в зависимости от температуры и давления. Удельная энтропия указана в таблице в интервале температуры от -50 до 50°С при давлении воздуха от 90 до 110 кПа. Следует отметить, что при нормальном атмосферном давлении (101,325 кПа) и температуре, например 30°С, удельная энтропия воздуха равна 0,1044 кДж/(кг·град).
 Источники:
Источники:
- Михеев М.А., Михеева И.М. Основы теплопередачи.
- Богданов С.Н., Бурцев С.И., Иванов О.П., Куприянова А.В. Холодильная теника. Кондиционирование воздуха. Свойства веществ: Справ./ Под ред. С.Н. Богданова. 4-е изд., перераб. и доп. — СПб.: СПбГАХПТ, 1999.- 320 с.
thermalinfo.ru
Средние изобарные объемные теплоемкости воздуха и газов
|
| |||||
СО2 | N2 | О2 | Н2О | сухой воздух | влажный воздух (d = 0,01) | |
0 | 1,5998 | 1,2946 | 1,3059 | 1,4943 | 1,2971 | 1,3188 |
100 | 1,7003 | 1,2958 | 1,3176 | 1,5062 | 1,3004 | 1,3243 |
200 | 1,7873 | 1,2996 | 1,3352 | 1,5223 | 1,3071 | 1,3318 |
300 | 1,8627 | 1,3067 | 1,3561 | 1,5224 | 1,3172 | 1,3423 |
400 | 1,9297 | 1,3168 | 1,3775 | 1,5664 | 1,3289 | 1,3544 |
500 | 1,9887 | 1,3276 | 1,3980 | 1,5897 | 1,3427 | 1,3682 |
600 | 2,0411 | 1,3402 | 1,4168 | 1,6148 | 1,3565 | 1,3829 |
700 | 2,0884 | 1,3536 | 1,4344 | 1,6412 | 1,3708 | 1,3976 |
800 | 2,1311 | 1,3670 | 1,4499 | 1,6680 | 1,3842 | 1,4114 |
900 | 2,1692 | 1,3796 | 1,4645 | 1,6957 | 1,3976 | 1,4248 |
1000 | 2,2035 | 1,3917 | 1,4775 | 1,7229 | 1,4097 | 1,4373 |
1100 | 2,2349 | 1,4034 | 1,4892 | 1,7501 | 1,4214 | 1,4499 |
1200 | 2,2638 | 1,4143 | 1,5005 | 1,7769 | 1,4327 | 1,4612 |
1300 | 2,2898 | 1,4252 | 1,5106 | 1,8028 | 1,4432 | 1,4725 |
1400 | 2,3136 | 1,4348 | 1,5202 | 1,8280 | 1,4528 | 1,4830 |
1500 | 2,3354 | 1,4440 | 1,5294 | 1,8527 | 1,4620 | 1,4926 |
1600 | 2,3555 | 1,4528 | 1,5378 | 1,8761 | 1,4708 | 1,5018 |
1700 | 2,3743 | 1,4612 | 1,5462 | 1,8996 | 1,4788 | 1,5102 |
1800 | 2,3915 | 1,4687 | 1,5541 | 1,9213 | 1,4967 | 1,5177 |
1900 | 2,4074 | 1,4758 | 1,5617 | 1,9423 | 1,4939 | 1,5257 |
2000 | 2,4221 | 1,4825 | 1,5692 | 1,9628 | 1,5010 | 1,5328 |
2100 | 2,4359 | 1,4892 | 1,5759 | 1,9825 | 1,5072 | 1,5399 |
2200 | 2,4484 | 1,4951 | 1,5830 | 2,0009 | 1,5135 | 1,5462 |
Таблица 3.3
К определению энтальпии продуктов сгорания
|
|
|
| ||||
|
|
|
|
| |||
0 | |||||||
200 | |||||||
… | |||||||
2000 | |||||||
|
|
|
|
| |||
|
| ||||||
0 | |||||||
200 | |||||||
… | |||||||
2000 | |||||||
п. 48.
Диаметр 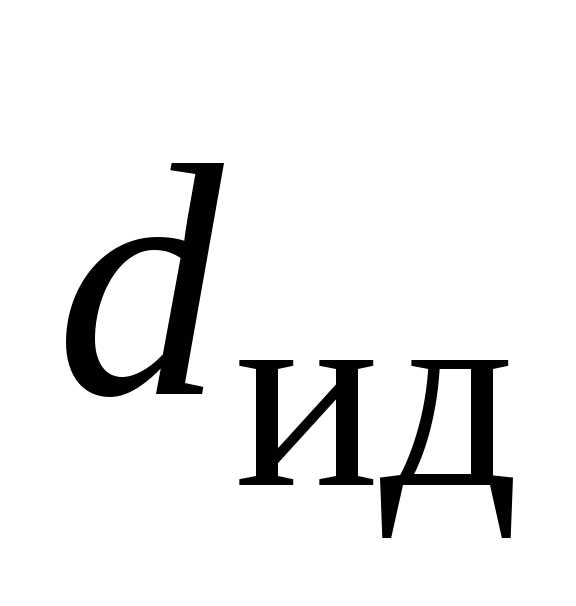 идеализированной топки следует
использовать при ее компоновке и
построении эскиза трубной части котла.
Форма труб и взаимное расположение
коллекторов должны соответствовать
аналогичным характеристикам котла,
изображенного на рис. 3.14. При построении
эскиза нужно стремиться к тому, чтобы
площадь фронта топки на эскизе была бы
равной
идеализированной топки следует
использовать при ее компоновке и
построении эскиза трубной части котла.
Форма труб и взаимное расположение
коллекторов должны соответствовать
аналогичным характеристикам котла,
изображенного на рис. 3.14. При построении
эскиза нужно стремиться к тому, чтобы
площадь фронта топки на эскизе была бы
равной  .
Масштаб 1:10.
.
Масштаб 1:10.
п. 49, 50. Эти геометрические характеристики топки определяют непосредственным измерением с эскиза котла, учитывая его масштаб. Эскиз котла следует выполнить на миллиметровой бумаге формата N11.
п. 54. Коэффициент экранирования топки котлов типа КАВ составляет 0,6 – 0,75.
п. 58.
Теоретическую температуру 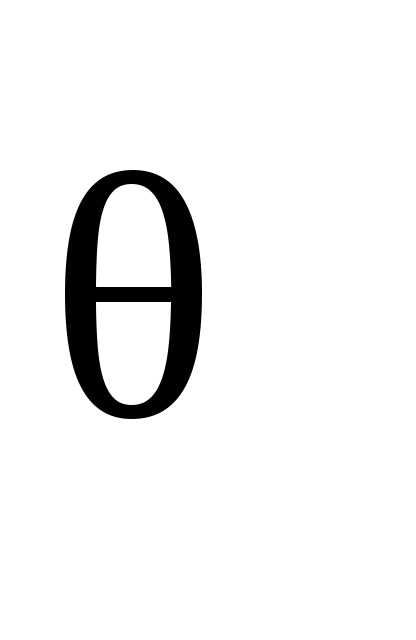 газов в топке определяют по предварительно
построенной диаграмме
газов в топке определяют по предварительно
построенной диаграмме  в зависимости от вычисленной в п. 57
энтальпии газов
в зависимости от вычисленной в п. 57
энтальпии газов 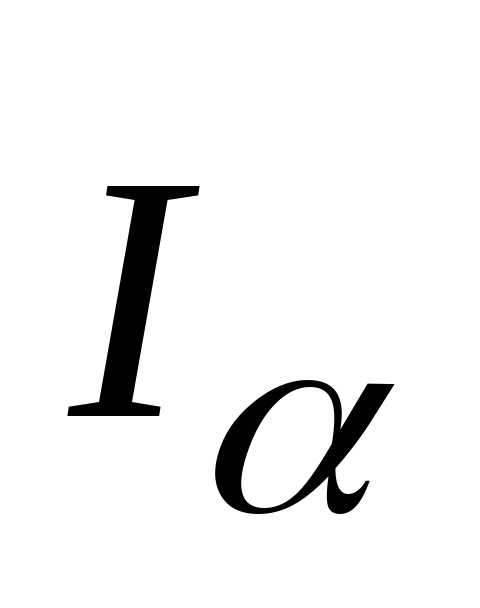 .
.
п. 65.
Расчетное значение 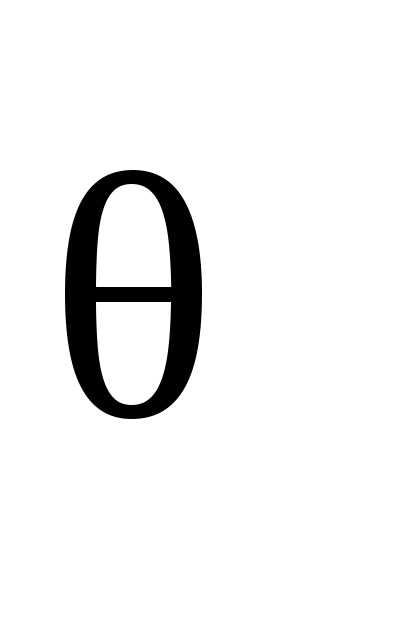 сравниваем с предварительно принятым.
Если |
сравниваем с предварительно принятым.
Если |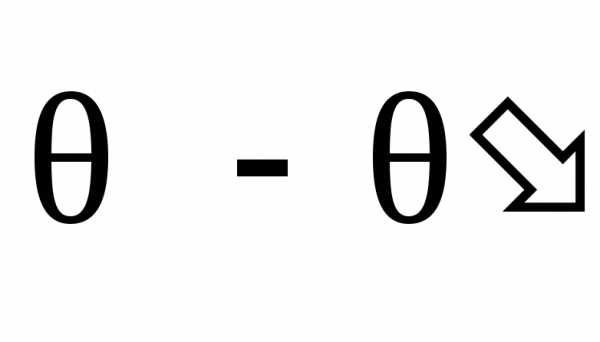 |
| 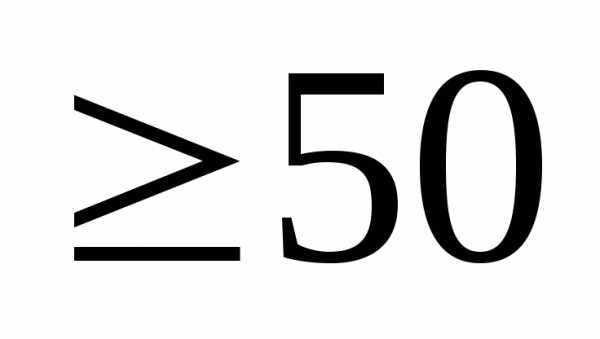 К, то принимаем
К, то принимаем 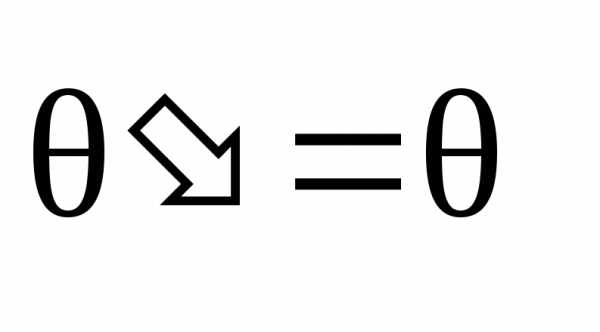 и проводим расчет вновь, начиная с п.
59.
и проводим расчет вновь, начиная с п.
59.
п. 69 – 71. Строение трубного пучка выбирают коридорное или шахматное; толщина стенки труб 2 и 2,5 мм; шаги труб в пучке выбирают такими, чтобы минимальное расстояние между кромками соседних отверстий было больше 8–10 мм.
п. 75. Расчетная длина труб пучка определяется по осевой линии средней трубки в пучке (см. рис. 3.14).
п. 97.
Если число рядов пучка 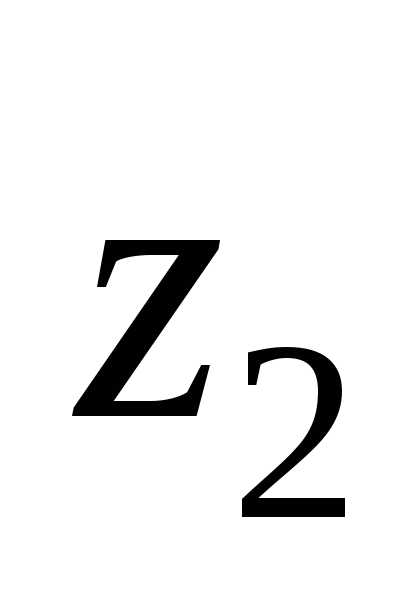 ,
полученное
расчетным путем, отличается от ранее
принятого
,
полученное
расчетным путем, отличается от ранее
принятого 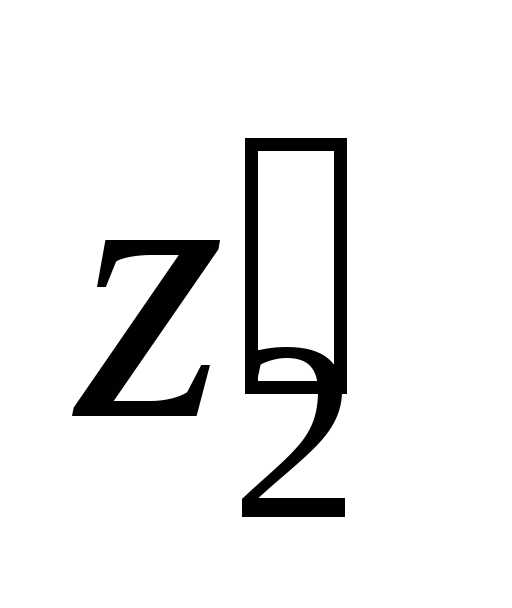 (п. 74), то разрешается расчет не повторять.
(п. 74), то разрешается расчет не повторять.
studfiles.net
26. Чем отличаются объемные и мольные теплоемкости воздуха?
Объемная теплоемкость- это количество теплоты , которую необходимо подвести к 1 м3 вещества ,чтобы нагреть его на 1 С,измеряется в (Дж/м3 К)
Мольная теплоемкость- это количество теплоты, которую необходимо подвести к 1молю вещества, чтобы нагреть его на 1 С, измеряется в (Дж/моль К)
27. Как определить теплоемкости газа – объемные, мольные, при постоянном объеме, при постоянном давлении?
μСр- средняя мольная теплоемкость при постоянном давлении.
μСv- средняя мольная теплоемкость при постоянном объеме.
μСр= μСv+μR, кДж/(кмоль∙град)
теплоемкость газов зависит от их температуры. Приближенно можно считать:
μСv=а+вТ,
где коэффициенты а и в для каждого газа имеют свои значения.
28. Чем объяснить, что при увеличении коэффициента наполнения цилиндра мощность двигателя возрастает?
Для увеличения мощности применяют наддув. При наддуве повышается наполнение цилиндра свежим зарядом и тем самым увеличивается давление у всасывающих клапанов что способствует возрастанию мощности. Мощность повышается пропорционально степени наддува.
При наддуве мощность увеличивается в 20…30% без изменения конструкции двигателя.
29. Выведите аналитического выражения для определения коэффициента наполнения.
Для сравнения ДВС с различными рабочими объемами используют коэффициент наполнения, представляющий отношение количества воздуха, фактически поступившего в цилиндр двигателя, к количеству воздуха, которое могло бы заполнить его рабочий объем Vh при температуре и давлении окружающей среды
Ма=Мо+Мr,
где Ma– количество молей рабочей смеси в точке «а»;
Мо– количество молей свежего заряда;
Mr– количество молей остаточных газов.
Вынося Моза скобки и обозначивМr/Mo=r(коэффициент остаточных газов), получаем:
Ма=Мо(1+r). Т.к.paVa=MaRTa*; иpoVo=MoRTo, то:
.
Подставив вместо Vo=vVh, получим:
Учтя, что 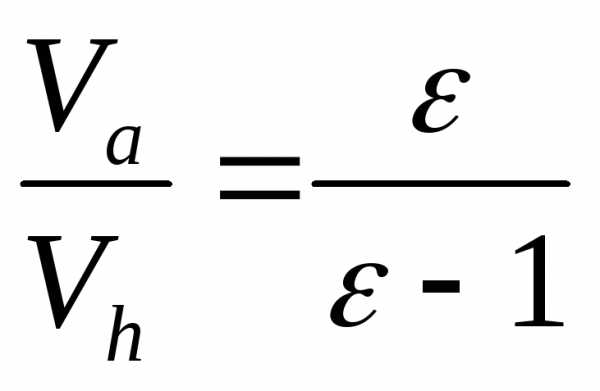 ,
запишем:
,
запишем:
. (4)
С учетом ранее полученного значения Таможно записать и такое выражение для определения коэффициента наполнения:
, (5)
В этих формулах: роиТо– давление и температура (в ДВС без наддува – окружающей среды, а с наддувом – после компрессора).
Отсюда следует, что на vвлияют подогрев зарядаtcm, температура Тои давлениероокружающей среды. Влияют на него такжеиr.
С увеличением tcm, т.е. степени подогрева смеси, v уменьшается. Так, увеличение ее от 5 до 20° снижает в некоторых двигателях v с 0,88 до 0,8 (почти на 10%).
30. Что из себя представляет круговые диаграммы фаз газораспределения двигателя?
Периоды
выраженные в градусах поворота коленчатого
вала в течение которых клапаны открыты,
называют фазами газораспределения. При
правильном выборе фаз не только улучшается
очистка цилиндров от продуктов сгорания
и заполнение его свежим зарядом, но и
может несколько сократиться затрата
энергии на газообмен, которая
пропорциональна разности давлений в
цилиндре в течение процессов выпуска
и впуска. 
studfiles.net
Определение изобарной теплоемкости воздуха
цель работы
Усвоение и закрепление теоретического материала по разделу технической термодинамики “Теплоемкость газов”, а также овладение одним из способов экспериментального определения теплоемкости воздуха.
Задание
Изучить схему экспериментальной установки, включить ее и вывести на заданный стационарный режим.
Провести опыт в соответствии с методическими указаниями, заполнить таблицу измерений.
Определить массовую изобарную среднюю теплоемкость воздуха.
Найти справочное значение массовой изобарной средней теплоемкости воздуха на заданном интервале температур.
Вычислить погрешность найденного значения массовой изобарной средней теплоемкости по отношению к табличному.
Сделать выводы по работе.
Методические указания
Удельной теплоемкостью называется количество тепла, которое необходимо подвести к единице количества вещества ( 1 кг , 1 моль , 1 м3 ), чтобы изменить его температуру на 1 градус. В связи с этим различают массовую с, кДж/(кг·град), мольную μc, кДж/(кмоль·град) и объемную с’, кДж/(м3·град) теплоемкости, которые связаны соотношениями:
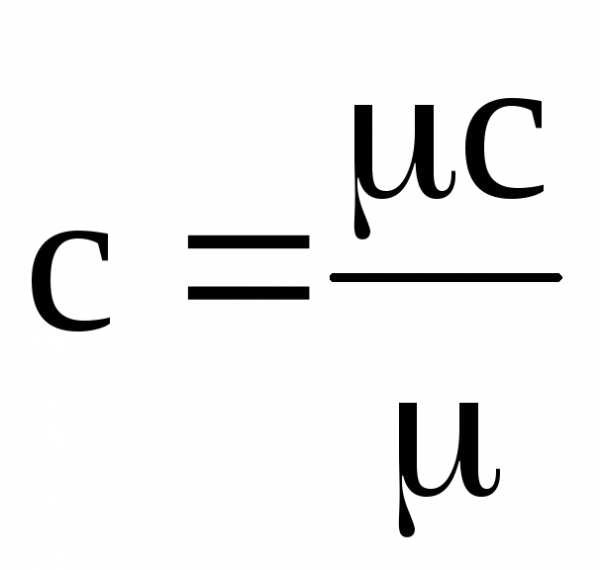 ;
;
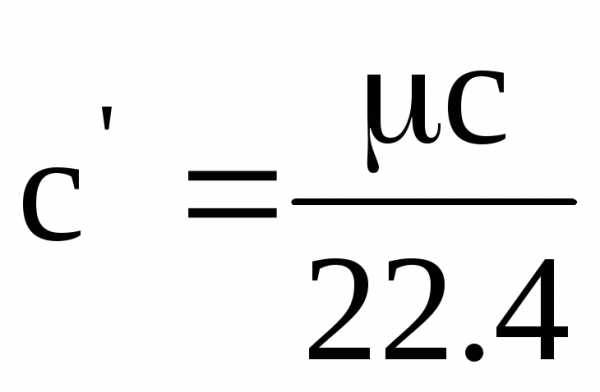 ;
(1)
;
(1)
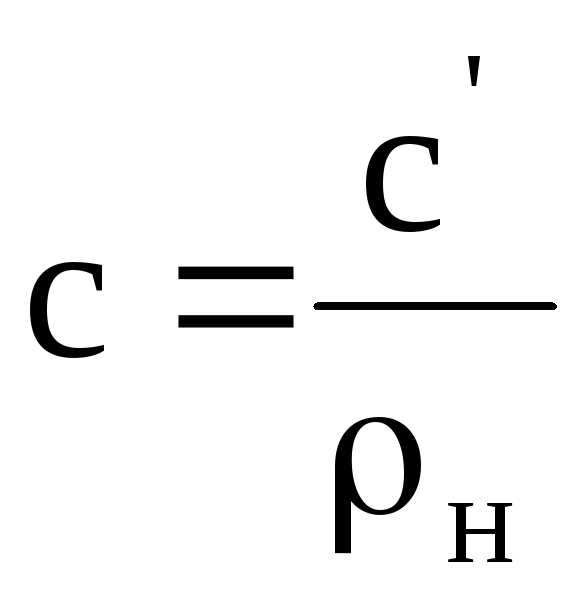 ,
,
где μ – молекулярная масса вещества, кг/моль;
ρн – плотность вещества при нормальных условиях ( t = 0 ˚С ,
p = 760 мм.рт.ст), кг/м3.
Поскольку подводимая к телу теплота зависит от характера процесса, теплоемкость будет свойством системы лишь в том случае, если процесс осуществляется при фиксированном значении какого-либо параметра системы:
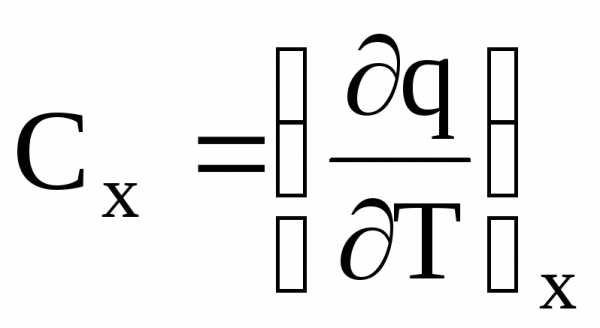 (2)
(2)
Теплоемкость при x = V = const называется изохорной (Cv), а при x = p = const – изобарной (Cp). Эти теплоемкости для идеальных газов связаны соотношением:
Cp –Cv = R , (3)
называемым уравнением Майера.
Определяемая выражением (2) теплоемкость при данной температуре называется истинной.
Если в процессе нагрева (охлаждения) при постоянном давлении участвует М кг газа, средняя массовая изобарная теплоемкость (Дж/(кг · град)) определяется по формуле
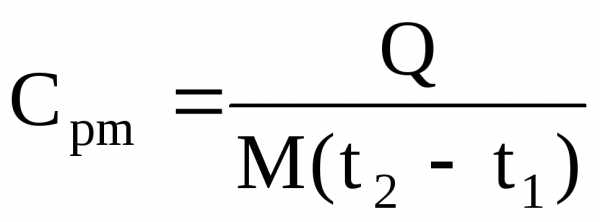 ,
,
где Q – количество теплоты, Дж;
( t2 – t1 ) – интервал температур, °С.
Данная формула положена в основу экспериментального определения изобарной теплоемкости воздуха.
Экспериментальная установка
2 5 1
Рисунок. Схема экспериментальной установки
Экспериментальная установка (рисунок) состоит из калориметрической стеклянной трубки 3, снабженной электронагревателем 4 и наружной теплоизолирующей оболочкой 5. Воздух вентилятором 10 продувается через калориметрическую стеклянную трубку 3. Расход воздуха регулируется автотрансформатором 9 и измеряется ротаметром 11. Мощность нагревателя регулируется автотрансформатором 8 и определяется по показателям амперметра 6 и вольтметра 7. Температура воздуха на входе и выходе из трубки измеряется термометрами 1 и 2, а абсолютное давление определяется по показаниям U-образного водяного манометра 12 и барометра 13.
studfiles.net
Определение изобарной теплоемкости воздуха
цель работы
Усвоение и закрепление теоретического материала по разделу технической термодинамики “Теплоемкость газов”, а также овладение одним из способов экспериментального определения теплоемкости воздуха.
Задание
Изучить схему экспериментальной установки, включить ее и вывести на заданный стационарный режим.
Провести опыт в соответствии с методическими указаниями, заполнить таблицу измерений.
Определить массовую изобарную среднюю теплоемкость воздуха.
Найти справочное значение массовой изобарной средней теплоемкости воздуха на заданном интервале температур.
Вычислить погрешность найденного значения массовой изобарной средней теплоемкости по отношению к табличному.
Сделать выводы по работе.
Методические указания
Удельной теплоемкостью называется количество тепла, которое необходимо подвести к единице количества вещества ( 1 кг , 1 моль , 1 м3 ), чтобы изменить его температуру на 1 градус. В связи с этим различают массовую с, кДж/(кг·град), мольную μc, кДж/(кмоль·град) и объемную с’, кДж/(м3·град) теплоемкости, которые связаны соотношениями:
;
; (1)
,
где μ – молекулярная масса вещества, кг/моль;
ρн – плотность вещества при нормальных условиях ( t = 0 ˚С, p = 760 мм.рт.ст), кг/м3.
Поскольку подводимая к телу теплота зависит от характера процесса, теплоемкость будет свойством системы лишь в том случае, если процесс осуществляется при фиксированном значении какого-либо параметра системы:
(2)
Теплоемкость при x = V = const называется изохорной (Cv), а при x = p = const – изобарной (Cp). Эти теплоемкости для идеальных газов связаны соотношением:
Cp –Cv = R , (3)
называемым уравнением Майера.
Определяемая выражением (2) теплоемкость при данной температуре называется истинной.
Если в процессе нагрева (охлаждения) при постоянном давлении участвует М кг газа, средняя массовая изобарная теплоемкость (Дж/(кг · град)) определяется по формуле
,
где Q – количество теплоты, Дж;
( t2 – t1 ) – интервал температур, °С.
Данная формула положена в основу экспериментального определения изобарной теплоемкости воздуха.
Экспериментальная установка
2 5 1
Рисунок. Схема экспериментальной установки
Экспериментальная установка (рисунок) состоит из калориметрической стеклянной трубки 3, снабженной электронагревателем 4 и наружной теплоизолирующей оболочкой 5. Воздух вентилятором 10 продувается через калориметрическую стеклянную трубку 3. Расход воздуха регулируется автотрансформатором 9 и измеряется ротаметром 11. Мощность нагревателя регулируется автотрансформатором 8 и определяется по показателям амперметра 6 и вольтметра 7. Температура воздуха на входе и выходе из трубки измеряется термометрами 1 и 2, а абсолютное давление определяется по показаниям U-образного водяного манометра 12 и барометра 13.
studfiles.net
Лабораторная работа № 2 Определение теплоёмкости воздуха при атмосферном давлении.
Цель
работы – определение изобарной
теплоёмкости воздуха 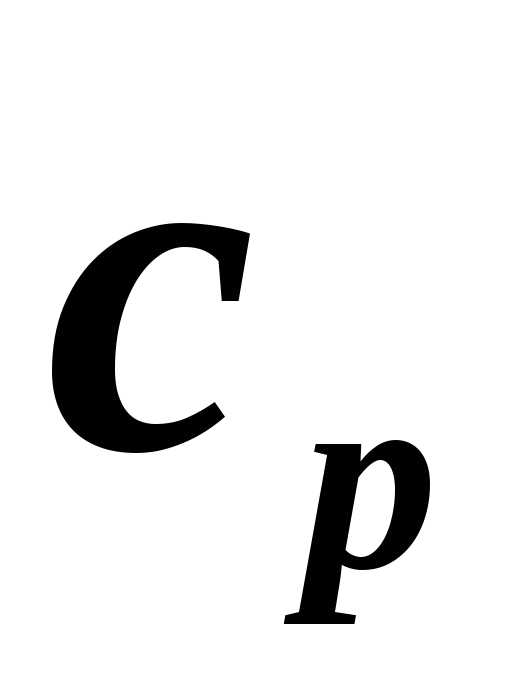 при атмосферном давлении и температуре,
близкой к комнатной. Определения проводят
методом протока. Теплоёмкость газов и
паров
при атмосферном давлении и температуре,
близкой к комнатной. Определения проводят
методом протока. Теплоёмкость газов и
паров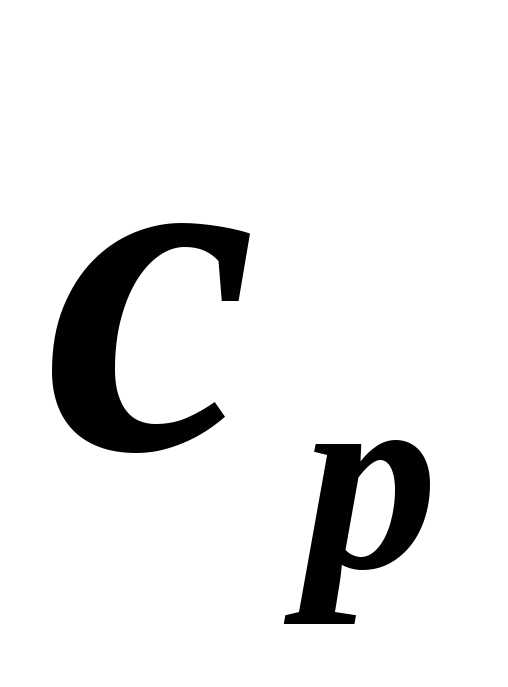 почти всегда определяют в проточном
калориметре. Для этого пропускают через
него газ , а в калориметре к газу подводят
теплоту. Схема калориметра показана на
рис.14
почти всегда определяют в проточном
калориметре. Для этого пропускают через
него газ , а в калориметре к газу подводят
теплоту. Схема калориметра показана на
рис.14
Рис.14
Для сечений 1 и 2 калориметра запишем полное уравнение первого закона термодинамики для потока (поток стационарный):
, (2.1)
где  – теплота, подведенная электронагревателем
к 1кг газа, который проходит через
калориметр;
– теплота, подведенная электронагревателем
к 1кг газа, который проходит через
калориметр; – тепловые потери в окружающую среду в
расчёте на 1кг газа.
– тепловые потери в окружающую среду в
расчёте на 1кг газа.
Так
как скорости газа 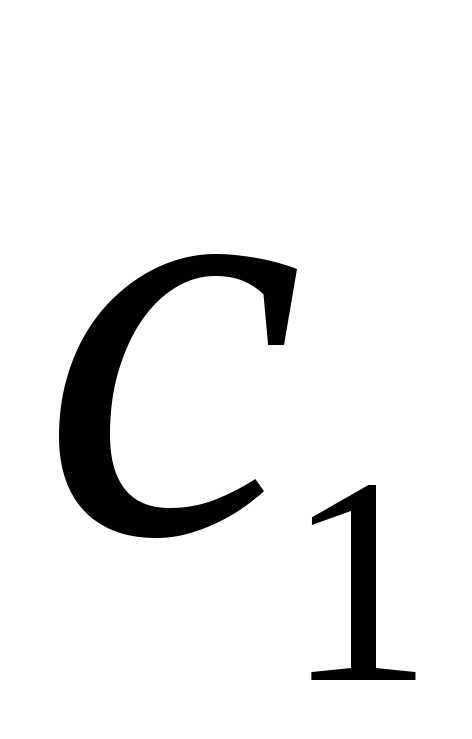 и
и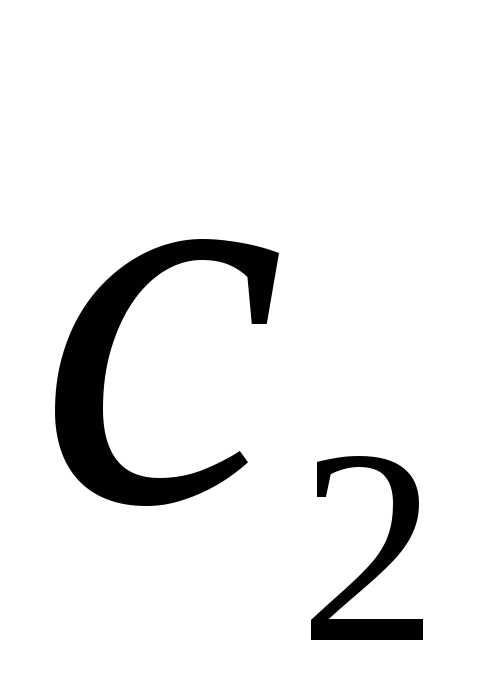 мало отличаются друг от друга, то
техническая работа не выполняется
мало отличаются друг от друга, то
техническая работа не выполняется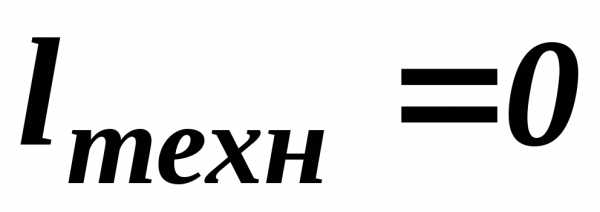 ,
разницейможно пренебрегать, так как,
соответственные члены из уравнения
(2.1) выпадают и остаётся
,
разницейможно пренебрегать, так как,
соответственные члены из уравнения
(2.1) выпадают и остаётся
. (2.2)
Воздух при атмосферном давлении по своим особенностям очень близок к идеальному газу, а энтальпия идеального газа зависит только от температуры, итак:

 .
(2.3)
.
(2.3)
Таким образом, для конечного повышения температуры
, (2.4)
где 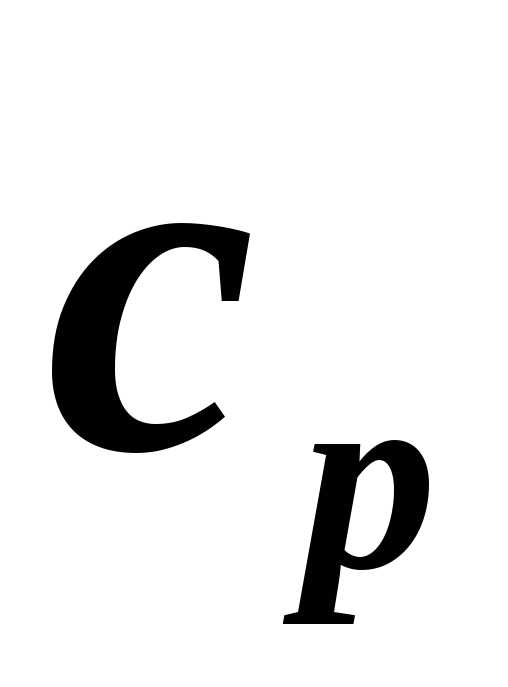 – средняя теплоёмкость в данном интервале
температур.
– средняя теплоёмкость в данном интервале
температур.
Подставляя разницу энтальпий из (2.4) в (2.2), получаем
(2.5)
Величины  и
и рассчитаны на 1кг газа. ДляМ кг газа,
теплота подведенная от нагревателя и
потери теплоты соответственно составляют:
рассчитаны на 1кг газа. ДляМ кг газа,
теплота подведенная от нагревателя и
потери теплоты соответственно составляют:
Вт; ,Вт;
и формула (2.5) принимает вид , (2.6)
Отсюда средняя массовая теплоёмкость при постоянном давлении составляет
(2.7)
Описание установки
Схема
установки для определения теплоёмкости
изображена на рис.15. Главный элемент
установки – проточный калориметр 2,
сделанный в виде стеклянной трубы с
двойными стенками, покрытыми серебром.
Пространство между оболочкой 3 и
внутренней трубой 2 вакуумизируют, что
позволяет свести к минимуму потери
теплоты в окружающую среду 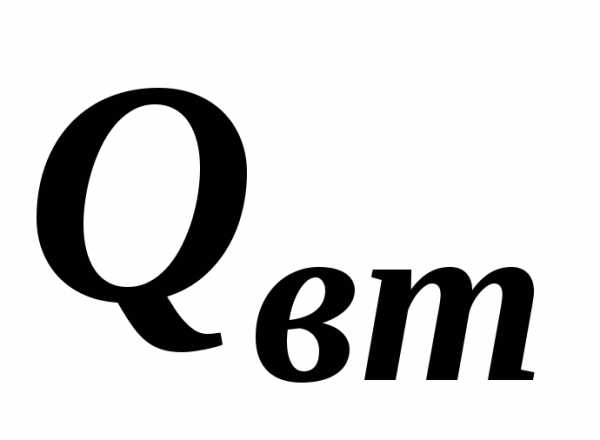 и не учитывать их при определении
теплоёмкости. Тогда.
Если мощность нагревателя равна
и не учитывать их при определении
теплоёмкости. Тогда.
Если мощность нагревателя равна ,Вт то
за час
,Вт то
за час  секунд количество
теплоты, отданной нагревателем,
составляет:
секунд количество
теплоты, отданной нагревателем,
составляет:
(2.8)
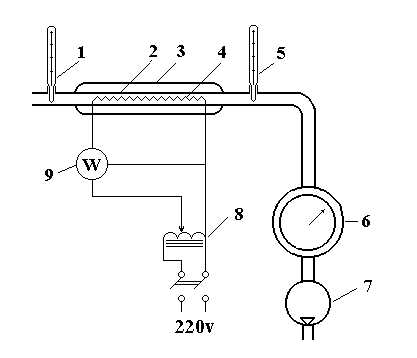
Рис.15 Схема исследовательской установки для определения изобарной теплоёмкости
Электронагреватель
4 (спираль), расположенный в середине
калориметра, и потребляет переменный
ток. Мощность нагревателя регулируется
путём изменения напряжения с помощью
автотрансформатора 8 и измеряется
ваттметром 9. Воздух в калориметр подаётся
вентилятором 7, температуры воздуха при
выходе t2 и на
входе t1 измеряются
термометрами 1,5. Объём воздуха, который
проходит через калориметр 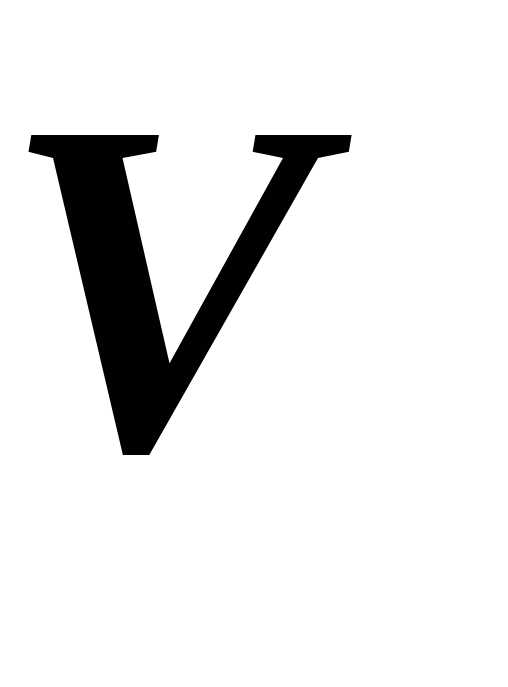 измеряют
счётчиком 6, время
измеряют
счётчиком 6, время  ,
за которое проходит измеренный объём
,
за которое проходит измеренный объём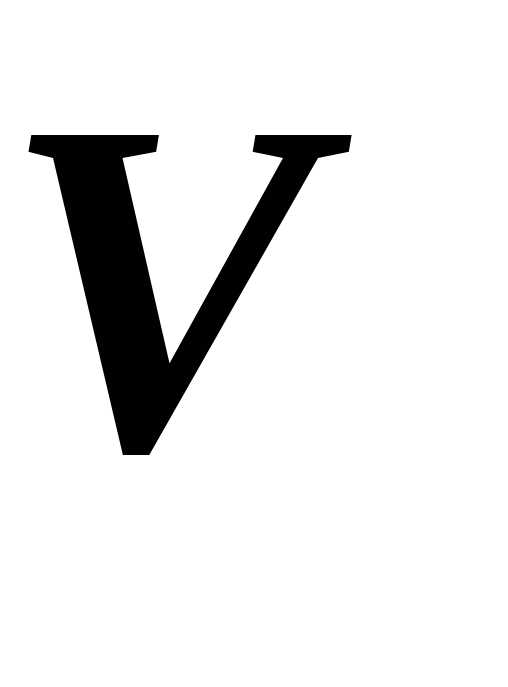 , измеряют
секундомером.
, измеряют
секундомером.
Выполнение работы и обработка её результатов.
В начале опыта необходимо включить вентилятор и установить определённый расход воздуха через калориметр. Затем включить нагреватель и, регулируя его мощность автотрансформатором, установить на выходе из калориметра постоянную температуру в пределах 35…40 С
После достижения стационарного режима, 3-4 раза с интервалом в 2 минуты выполнить запись параметров всех устройств. Следует считать, что стационарный режим будет достигнут тогда, когда температура на выходе из калориметра станет постоянной. Опыты проводят при разных мощностях нагревателя. После завершения опыта надо выключить нагреватель, вентилятор и измерить давление воздуха Р барометром, который есть в лаборатории.
Во всех дальнейших расчётах используют среднее во время опыта значение параметров, которое определяют как среднеарифметическое из записанных показателей данного устройства.
Масса воздуха М рассчитывается по объёму V, померенному измерителем по уравнению Менделеева-Клапейрона
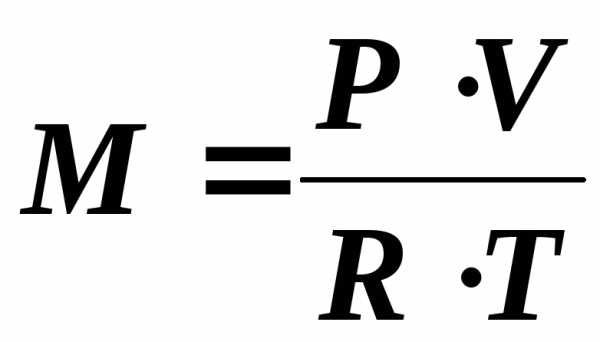 ‚
кг/с , (2.9)
‚
кг/с , (2.9)
где Р – атмосферное давление, Па, которое
измеряется барометром; 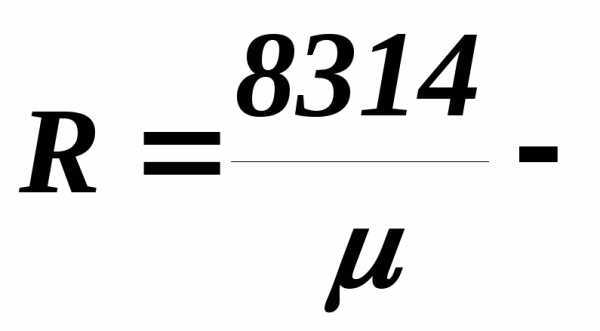 газовая
постоянная воздуха,Дж/
кг К;
газовая
постоянная воздуха,Дж/
кг К;
T– температура воздуха в лаборатории равна температуре при входе в калориметр, К.
Расход воздуха через калориметр составляют:
. (2.10)
Учитывая выражения (2.8) и (2.10) формула для определения средней массовой изобарной теплоёмкости (2.7) принимает вид:
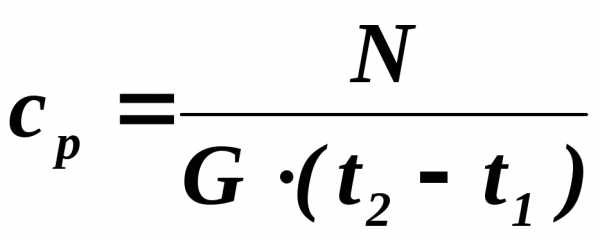 ‚ Дж/кг
К (2.11)
‚ Дж/кг
К (2.11)
где N– мощность нагревателя.
Объёмная изобарная теплоёмкость определяется по формуле:
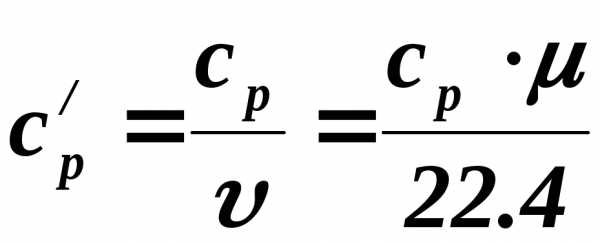 ,Дж/м3 К (2.12)
,Дж/м3 К (2.12)
где 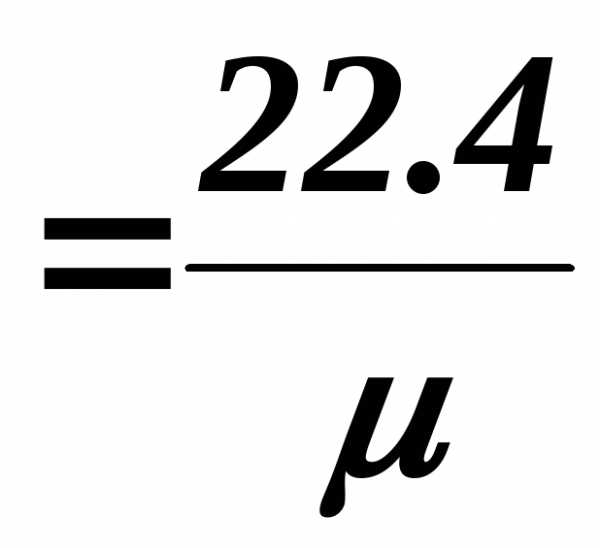 – удельный объём воздуха при н.у., м3/кг
– удельный объём воздуха при н.у., м3/кг
studfiles.net
Изохорная массовая теплоёмкость воздуха по уравнения Майера составляет
,Дж/кг К (2.13)
Экспериментальное исследование теплоёмкости газа даёт возможность на основании полученных данных вычислить его энтальпию и внутреннюю энергию.
Таблица 2.
№ п/п | Наименование | Формула | Розмер-ность | Численное значение | |||
1 | Объём воздуха по показанию счётчика | | |||||
2 | Время по показанию секундомера |
| С | ||||
3 | Мощность нагревателя | | Вт | ||||
4 | Температура на входе до калориметра | | оС | ||||
5 | Температура на выходе из калориметра | | оС | ||||
6 | Атмосферное давление | Р | мм рт. ст. | ||||
Па | |||||||
7 | Газовая постоянная воздуха | | | ||||
8 | Масса воздуха,имеющего объём, V | | кг | ||||
9 | Массовыйрасход воздуха |
| | ||||
10 | Массоваяизобарная теплоёмкость | | | ||||
11 | Объёмная изобарная теплоёмкость | | | ||||
12 | Массоваяизохорнаятеплоёмкость | | |||||
13 | Энтальпия воздуха | | | ||||
Если начало отсчёта энтальпии, то есть i= 0, взять при t = О °С, то значение энтальпии идеального газа можно вычислить в кДж/кг по формуле
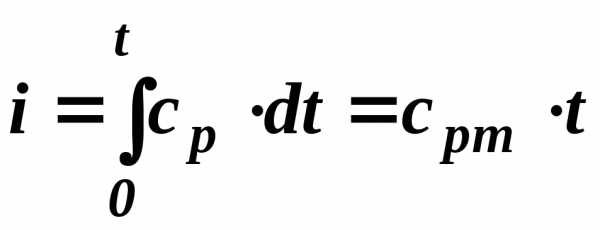 (2.14)
(2.14)
По
этому уравнению можно вычислить энтальпию
воздуха при температуре 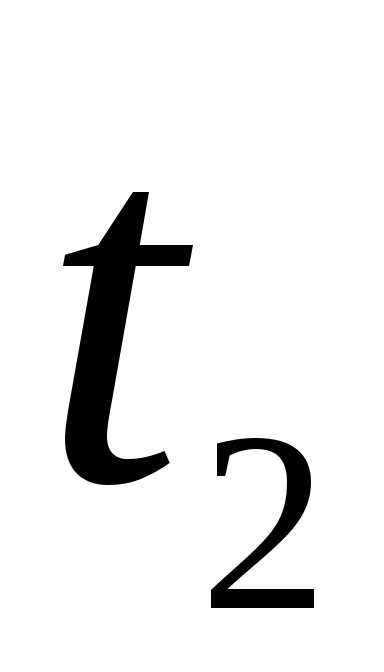 на выходе из калориметра во время опыта.
При этом следует учитывать, что
теплоёмкостьСр не зависит от температуры. Результаты
измерений вносят в табл.2
на выходе из калориметра во время опыта.
При этом следует учитывать, что
теплоёмкостьСр не зависит от температуры. Результаты
измерений вносят в табл.2
Контрольные вопросы
1. Определение теплоёмкости.
2. Какие различают теплоёмкости?
3. От чего зависит теплоёмкость?
4. Как определить теплоту процесса, если известна теплоёмкость?
5. Определить теплоту, которую надо подвести к воде в чайнике, чтобы довести её до кипения.
6.
Почему 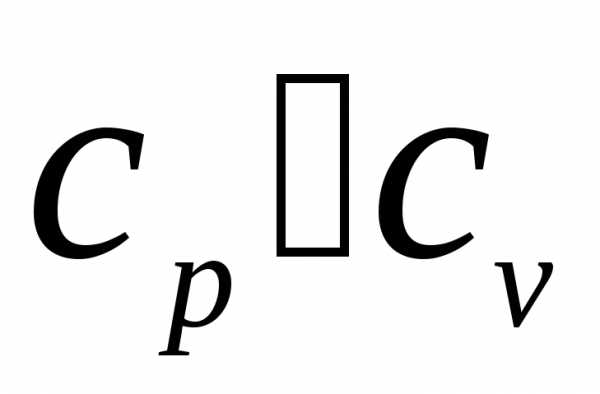 ?
?
7. В каких процессах ?
8. Как зависит теплоёмкость идеального газа от показателя политропа?
9. Изобразить на диаграммах в P– и T–s координатах процесс, который происходит в калориметре.
Лабораторная работа №3 Исследование изохорного процесса
Процесс, который происходит при постоянном объёме, называется изохорным. Математическая связь между параметрами в изохорном процессе определяется законом Шарля:
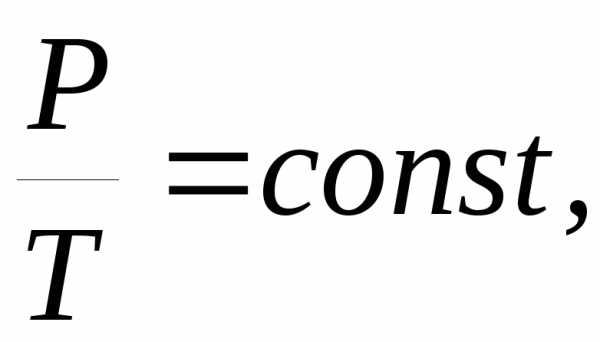 или
или 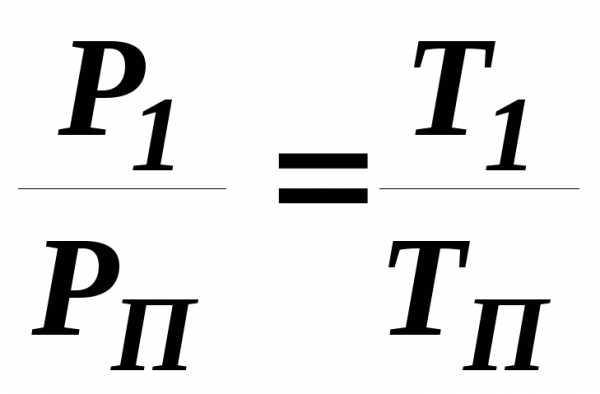 (3.1)
(3.1)
т.е.
при постоянном объёме давление газа
изменяется прямопропорционально его
абсолютной температуре, изохоры показаны
на диаграммах рис.16. Процесс П-1 – изохорный подвод теплоты, П-2 – изохорный отвод теплоты. Уравнение
первого закона термодинамики для
изохорного процесса имеет вид (работа
не выполняется 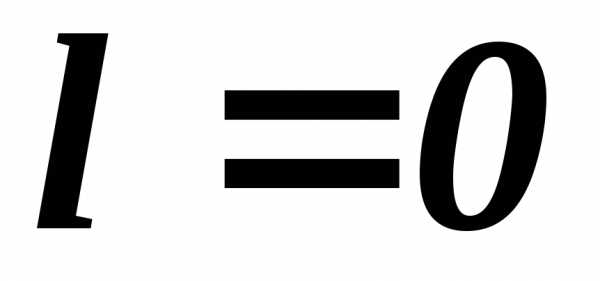 )
)
 (3.2)
(3.2)
Количество теплоты и изменение внутренней энергии в изохорном процессе определяется по формуле ( при CV=const )
(3.3)
Рис.16
Таким
образом, вся полученная теплота в
изохорном процессе расходуется только
на изменение внутренней энергии. В T-s диаграмме
площадь под процессом П
–1 равна
теплоте процесса (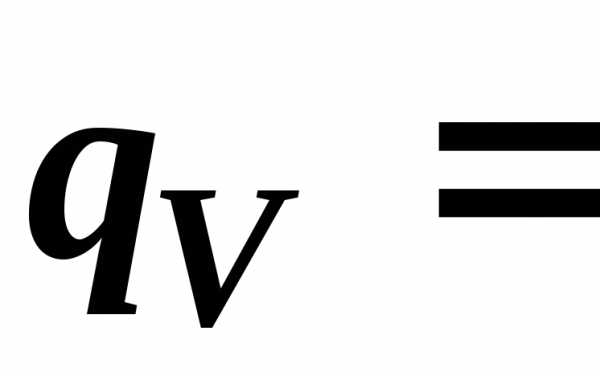 пл
П-1-3-4 ). При
незначительных изменениях температур,
которые имеют место в опытах, зависимостью
теплоёмкости от температуры можно
пренебрегать, среднюю изохорную
теплоёмкость воздуха можно считать
постоянной
пл
П-1-3-4 ). При
незначительных изменениях температур,
которые имеют место в опытах, зависимостью
теплоёмкости от температуры можно
пренебрегать, среднюю изохорную
теплоёмкость воздуха можно считать
постоянной
кДж/кгK (3.4)
Описание установки
Схема установки для проведения опытов показана на рис.17. Опыт проводится с воздухом, который находится в середине герметичной посудины 7. Посудина 7 погружена в воду, которая налита в термостат 12. Температура воды в термостате увеличивается электронагревателем 9. Значение температуры воды задаётся электроконтактным термометром 10. При достижении заданной температуры воды, нагреватель выключается, сигнальная лампочка 11 гаснет. Равномерность температуры воды обеспечивается электромешалкой 6. Избыточное (манометрическое) давление измеряется манометром 5. Температура воздуха определяется с помощью термопары, горячий спай 7 которой расположен в середине герметичной посудины, а холодный 2 – в пробирке с маслом 1. Показания термопары измеряется цифровым вольтметром 4. Температуру холодного спая 2 измеряют термометром 3.
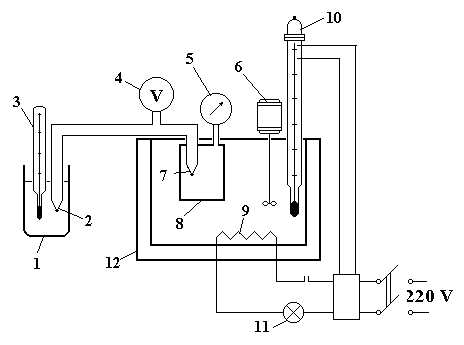
Рис.17 Схема установки для исследования изохорного процесса.
Выполнение работы.
1. Первый отсчёт выполняют при выключенном электронагревателе термостата. При этом фиксируют показания манометра 5 Рман, давление окружающей среды Ратм – барометром, ЭДС термопары – вольтметром. ЭДС позволяет определить температуру воздуха в посудине.
2. Устанавливают на электроконтактном термометре 10 температуру на 5оС больше, чем предыдущую, включают нагреватель термостата 9. Когда температура воды достигает заданной, гаснет сигнальная лампочка 11. После этого начинают фиксировать показания термопары вольтметром через каждые две минуты. Окончательное значение показаний вольтметра и манометра фиксируют тогда, когда предыдущие и дальнейшие показания термопары будут одинаковыми.
3. Устанавливают на электроконтактном термометре последовательно ещё 4 значения температур через каждые 5оС и измеряют ЭДС термопары и избыточное давление.
Обработка результатов работы
1. Результаты измерений и расчётов заносят в таблицу 3
Таблица 3
№ п/п | Наименование | Формула | Размерность | Числовые значения | ||||
1 | Избыточное давление | | | |||||
| ||||||||
2 | Атмосферное давление | Ратм | | |||||
мм рт. ст. | ||||||||
3 | Абсолютное давление | | ||||||
4 | ЭДС термопары | | | |||||
5 | ЭДС холодного спая | | ||||||
6 | ЭДС гарячего спая | |||||||
7 | Температура воздуха | | | |||||
| ||||||||
8 | Внутренняя энергия | | ||||||
2. На графике в T–P координатах наносят полученные точки и строят прямую T = a P, коэффициент а определяют по методу наименьших квадратов.
3. Пользуясь значением средней теплоёмкости, по формуле (3.4) считают величину внутренней энергии для каждого опыта. На начало отсчёта внутренней энергии принимают u0=0 при t = 0 0C .
4. Строят график
5. Рассчитывают изменение внутренней энергии для отдельных процессов.
studfiles.net
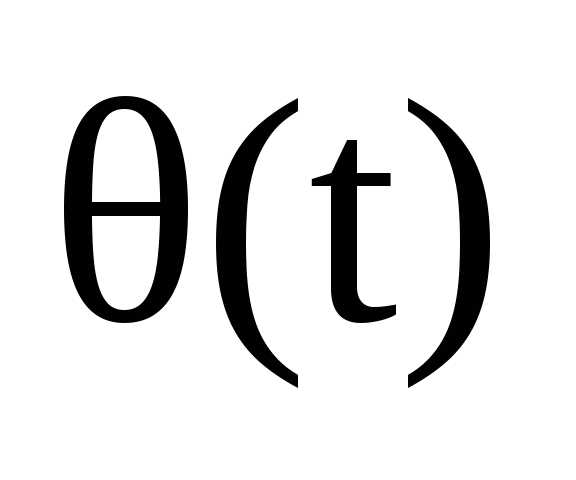 °С
°С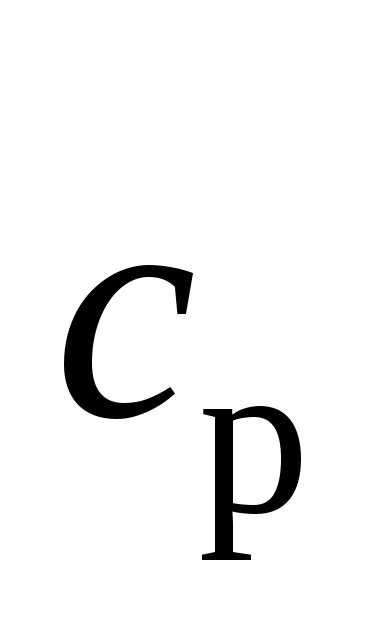 ,
кДж/(м3∙°С)
,
кДж/(м3∙°С) ,
°С
,
°С =…м2/кг
=…м2/кг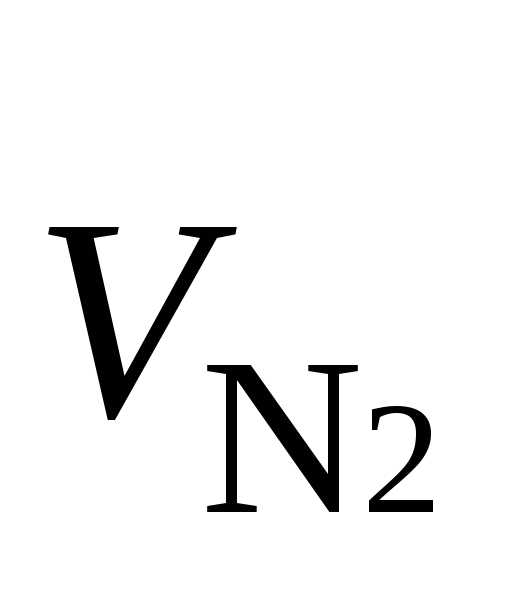 =…м2/кг
=…м2/кг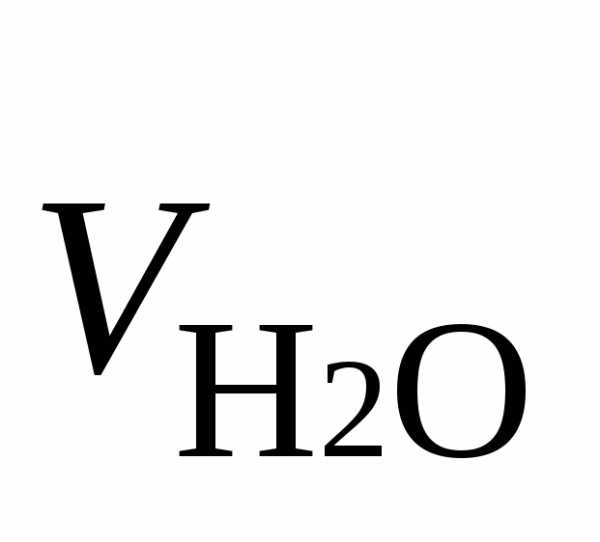 =…м2/кг
=…м2/кг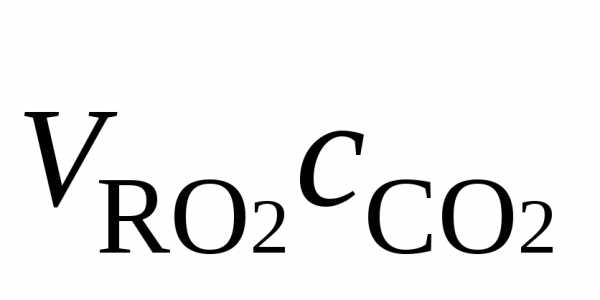
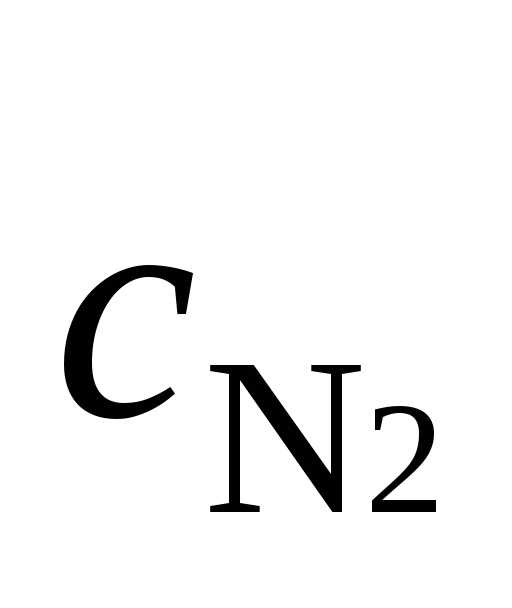
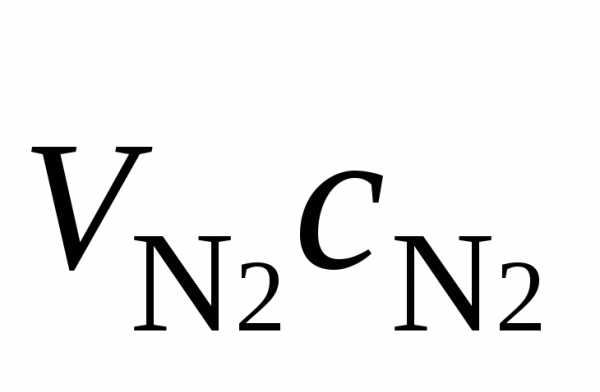
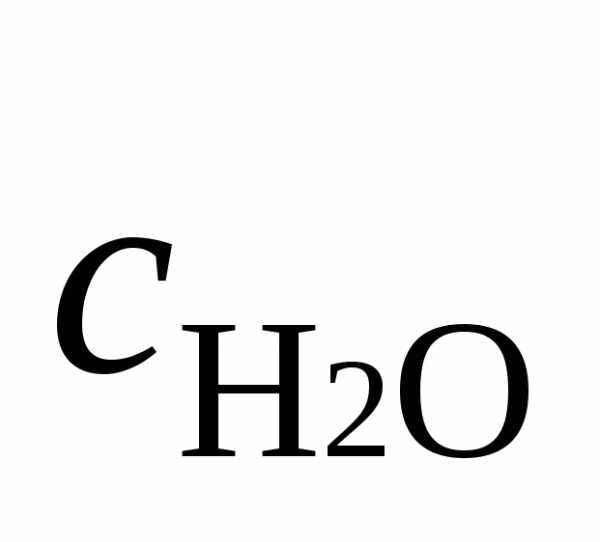
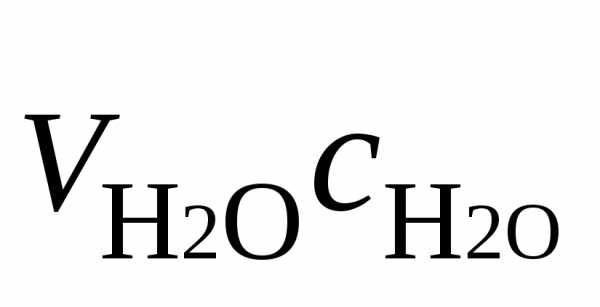
 ,
°С
,
°С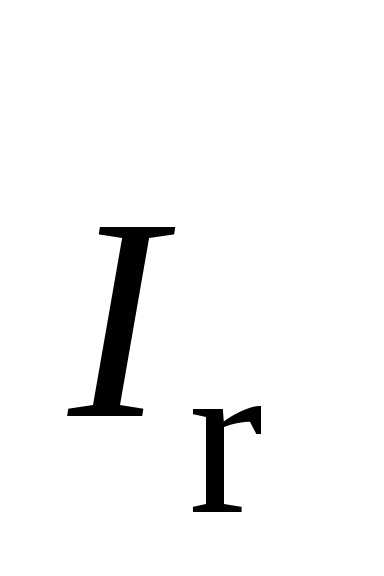 ,
МДж/кг
,
МДж/кг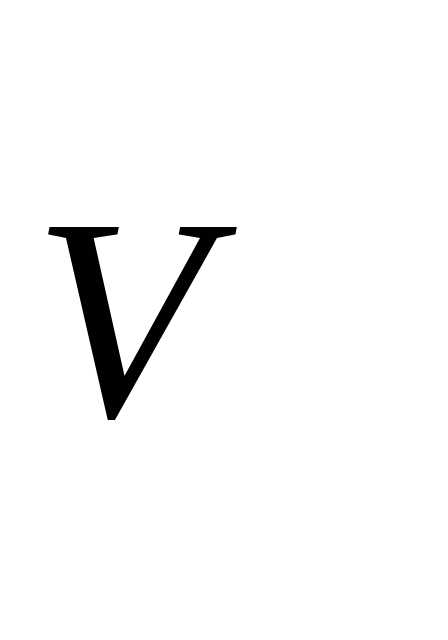 =…м2/кг
=…м2/кг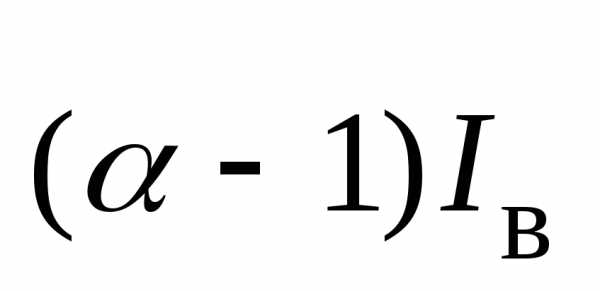 ,
МДж/кг
,
МДж/кг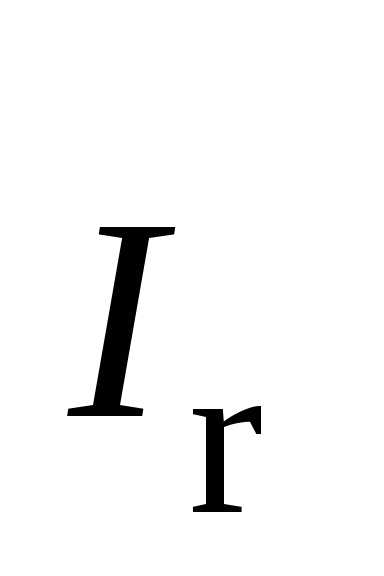 ,
МДж/кг
,
МДж/кг