Тепловая скорость – частица – Большая Энциклопедия Нефти и Газа, статья, страница 1
Тепловая скорость – частица
Cтраница 1
Тепловые скорости частиц в плоскости ( х, у) в этой модели учитываются косвенно тем, что диску приписывается распределение поверхностной плотности, совпадающее с распределением1 объемной плотности р0 ( г) в исходной стационарной модели. Предполагаем, что диски все время остаются ориентированными параллельно-плоскости ( х, у) и свободно проходят один сквозь другой. [1]
Заметим, что собственные тепловые скорости частиц, которые с точностью до численного коэффициента всегда совпадают со скоростью звука. [2]
Для того чтобы учесть влияние тепловых скоростей частиц и столкновений, рассмотрим моменты функции распределения в сопутствующей системе координат. [4]
В рассматриваемом случае, когда дрейфовая скорость иона много
Как видно, скорость звука в газе УуТ / М оказывается порядка тепловой скорости частиц. [6]
В плазме существуют колебания, фазовая скорость к-рых намного меньше скорости света и даже тепловой скорости частиц; к их числу относятся ленгмюровские колебания, ионно-звуковые и альфеновские волны и др. Такие волны легко возбуждаются нерелятивистскими пучками заряж. Но, обладая малыми фазовыми скоростями, такие волны заперты в плазме, не излучаются, а со пременем диссипируют, поглощаясь частицами плазмы. Именно поэтому возбуждение медленных волн в плазме нерелятивистскими пучками заряж. [7]
При взаимодействии магнитного поля Земли с солнечным ветром возникает стоячая ударная волна, ибо направленная скорость плазмы превышает тепловую скорость частиц – скорость звука. [8]
Вычислим коэффициент диффузии в двух предельных случаях – в одном из них дрейфовая скорость иона мала по сравнению с тепловой скоростью частиц газа, в другом выполняется обратное соотношение. При этом мы воспользуемся тем, что ширина функции распределения по скоростям мала по сравнению с характерными значениями скорости. [9]
Займемся теперь изучением тех последствий, которые вызывает инжекция в плазму моноэнергетического или холодного пучка электронов малой плотности, движущегося через плазму со скоростью v0t много большей тепловой скорости частиц плазмы. [10]
Задача 4.18. Ионы, масса которых совпадает с массой частиц газа, движутся в сильном электрическом поле, так что дрейфовая скорость иона значительно превышает
В случае, если масса иона значительно превышает массу частицы газа, то энергия движения частиц поперек поля не зависит от напряженности поля, пока дрейфовая скорость иона много меньше тепловой скорости частиц газа. При высоких напряжен-ностях электрического поля средняя кинетическая энергия иона обусловлена его движением в направлении поля. [12]
Мы уже видели при рассмотрении продольных колебаний электронной плазмы, что мнимая часть диэлектрической проницаемости мала ( а поэтому сравнительно невелико поглощение волн), если фазовая скорость значительно превышает тепловую скорость частиц. [13]
Дрейфовая скорость иона значительно превышает тепловую скорость частиц газа. [14]Строго говоря, параболическое уравнение лишь приближенно описывает процесс теплопроводности. На самом деле скорость распространения тепла конечна и не превышает ( при молекулярной или электронной теплопроводности) тепловой скорости частиц. [15]
Страницы: 1 2
www.ngpedia.ru
Роль быстрых молекул
При любой температуре имеется некоторое количество молекул, скорости которых, а значит, и кинетические энергии, заметно превышают средние.
Известно,
что многие химические реакции, например
горение обычных видов топлива (дрова,
уголь и т. д.), начинаются только при
определенной, достаточно высокой
температуре. Энергия, необходимая для
начала процесса окисления топлива, т.
е. горения (ее называют энергией
активации), имеет порядок 10
Испарение жидкости также определяется быстрыми молекулами правого «хвоста» максвелловского распределения. Энергия связи молекул воды при комнатной температуре значительно больше kT. Тем не менее испарение происходит за счет небольшого числа быстрых молекул, у которых кинетическая энергия превышает kT.
Максвелл открыл новый тип физического закона — статистический и нашел распределение молекул по скоростям. Он отчетливо понимал значение своего открытия. В докладе Кембриджскому философскому обществу Максвелл сказал: «Я считаю, что наиболее важное значение для развития наших методов мышления молекулярные теории имеют потому, что они заставляют делать различие между двумя методами познания, которые мы можем назвать динамическим и статистическим».
§ 4.7. Измерение скоростей молекул газа
Основное уравнение молекулярно-кинетической теории газов (4.4.9) было получено на основе модели идеального газа. При этом было сделано несколько упрощающих реальную картину предположений. Чтобы убедиться в допустимости сделанных предположений, нужно проверить экспериментально вытекающие из уравнения
Средняя скорость теплового движения молекул
Из сопоставления уравнения (4.4.9) с термодинамическим уравнением состояния идеального газа было получено выражение (4.5.5) для средней кинетической энергии поступательного движения молекул:
Отсюда средний квадрат скорости поступательного движения равен:
(4.7.1)
Квадратный корень из этой величины называется средней квадратичной скоростью:
(4.7.2)
Средняя
квадратичная скорость мало отличается
от наиболее вероятной скорости,
определяемой выражением (4.6.9). Так как
постоянная Больцмана равна отношению
универсальной газовой постоянной к
постоянной Авогадро 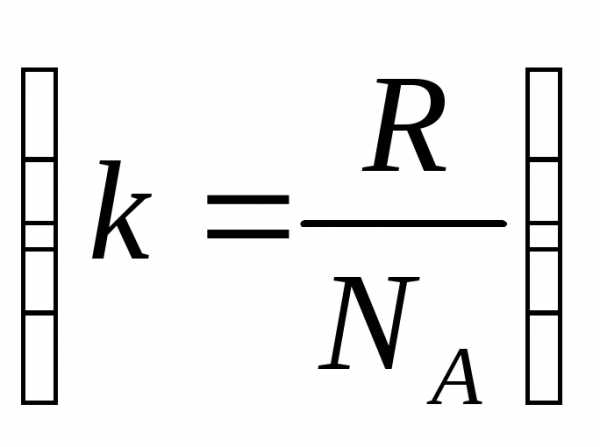
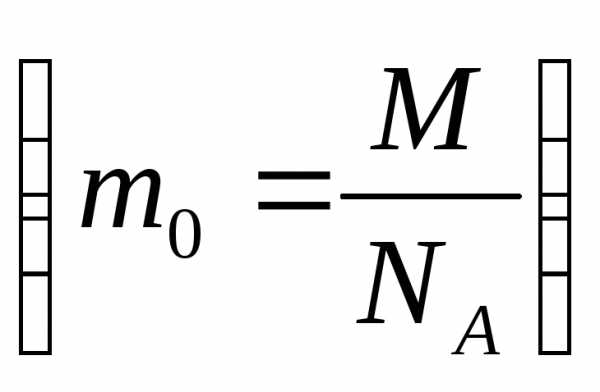 ,
то из формулы (4.7.2) получается:
,
то из формулы (4.7.2) получается:(4.7.3)
Вычисленные
по этой формуле скорости  для
различных газов при t = 0
°С (Т =
273 К) приведены в таблице 1.
для
различных газов при t = 0
°С (Т =
273 К) приведены в таблице 1.
Таблица 1
Газ | | Газ | |
Водород Азот | 1838 493 | Кислород Углекислый газ | 641 393 |
Как видно из таблицы, скорости молекул очень велики — порядка скорости артиллерийских снарядов — и несколько больше скорости звука в соответствующем газе. На первых порах такой результат вызвал замешательство среди физиков. Ведь если скорости молекул столь велики, то как объяснить, например, что запах духов, пролитых в комнате, распространяется довольно медленно; должно пройти несколько секунд, чтобы запах распространился по всей комнате. Однако объяснить этот факт оказалось довольно просто. Молекулы газа, несмотря на свои малые размеры, непрерывно сталкиваются друг с другом. Из-за большой скорости движения молекул число столкновений молекул воздуха в 1 с при нормальных атмосферных условиях достигает нескольких миллиардов.
Средняя длина свободного пробега молекулы оказывается равной 10-4—10-5см. Поэтому траектория каждой молекулы представляет собой очень запутанную ломаную линию (рис. 4.14). Большие скорости молекула имеет на прямолинейных отрезках ломаной. Перемещение же молекулы в каком-либо направлении в среднем невелико даже за время порядка нескольких секунд. При перемещении молекулы из точки А в точку В пройденный ею путь оказывается гораздо больше расстояния АВ.
Рис. 4.14
studfiles.net
Тепловая скорость — Википедия. Что такое Тепловая скорость
Материал из Википедии — свободной энциклопедииЕсли распределение частиц по скоростям задано некоторой функцией f(v){\displaystyle f(v)}, то тепловая скорость определяется как:
- vT=[∫0∞v2f(v)dv]1/2{\displaystyle v_{T}=\left[\int \limits _{0}^{\infty }v^{2}f(v)dv\right]^{1/2}}
В случае максвелловского распределения по скоростям, определяемого температурой T, тепловая скорость равна:
- vT=3kTm{\displaystyle v_{T}={\sqrt {\frac {3kT}{m}}}}
где k — постоянная Больцмана, m — масса частиц. Таким образом, тепловая скорость частиц и температура вещества однозначно связаны между собой.
Тепловая скорость характеризует среднюю кинетическую энергию частиц вещества:
- <Ek>=mvT22{\displaystyle <E_{k}>={\frac {mv_{T}^{2}}{2}}}
Таким образом, тепловая скорость также характеризует и внутреннюю энергию вещества, связанную с поступательным движением составляющих его частиц.
Литература
- Сивухин Д. В. Общий курс физики. — Т. II. Термодинамика и молекулярная физика. — С. 193—196.
wiki.sc
Тепловая скорость — Википедия
Материал из Википедии — свободной энциклопедии
Теплова́я ско́рость — значение среднеквадратичной скорости теплового движения частиц.
Если распределение частиц по скоростям задано некоторой функцией f(v){\displaystyle f(v)}, то тепловая скорость определяется как:
- vT=[∫0∞v2f(v)dv]1/2{\displaystyle v_{T}=\left[\int \limits _{0}^{\infty }v^{2}f(v)dv\right]^{1/2}}
В случае максвелловского распределения по скоростям, определяемого температурой T, тепловая скорость равна:
- vT=3kTm{\displaystyle v_{T}={\sqrt {\frac {3kT}{m}}}}
где k — постоянная Больцмана, m — масса частиц. Таким образом, тепловая скорость частиц и температура вещества однозначно связаны между собой.
Тепловая скорость характеризует среднюю кинетическую энергию частиц вещества:
- <Ek>=mvT22{\displaystyle <E_{k}>={\frac {mv_{T}^{2}}{2}}}
Таким образом, тепловая скорость также характеризует и внутреннюю энергию вещества, связанную с поступательным движением составляющих его частиц.
Литература
- Сивухин Д. В. Общий курс физики. — Т. II. Термодинамика и молекулярная физика. — С. 193—196.
wiki2.red
Тепловая скорость – Энциклопедия по машиностроению XXL
При достаточно высоких частотах акустическая длина волны становится настолько малой, что начинает приближаться к длине свободного пробега молекул газа. В этом случае основное уравнение для с (3.36) и уравнения для ак-г и ао перестают выполняться, так как все они получены в предположении, что газ представляет собой непрерывную среду. Согласно кинетической теории, тепловая скорость молекул в газе имеет тот же порядок, что и скорость звука. Таким образом, если длина звуковой волны по порядку величины приближается к средней длине свободного пробега, то звуковая частота должна приближаться к частоте соударений между молекулами. Это очень высокая частота порядка 10 Гц, так как средняя длина свободного пробега при комнатной температуре составляет величину порядка 100 нм. В акустической термометрии столь высокие частоты никогда не применяются, самая высокая частота, на [c.105]Воспользовавшись выражением для расчета тепловой скорости молекул [c.151]
При наложении электрического поля возникают силы, заставляющие электроны дрейфовать — двигаться вдоль поля на хаотическое тепловое движение накладывается упорядоченное движение со скоростью дрейфа. Пользуясь законами классической физики, можно оценить ее порядок по сравнению с тепловой скоростью. [c.33]
Рост температуры металла ведет к увеличению тепловой скорости электрона, а увеличение амплитуды колебаний ионов в узлах решетки уменьшает пробег X электрона, поэтому у металлов с увеличением температуры и пластической деформации проводимость уменьшается. [c.34]
Теплопроводность плазмы также обусловлена движением частиц. Главную роль в переносе теплоты от более горячих участков плазмы к холодным играют электроны (благодаря большей тепловой скорости). Если вдоль некоторого направления существует перепад температур, то электроны с большими энергиями идут в одну сторону, а с меньшими — в другую. [c.57]
Продольное поле. При наложении продольного поля направления магнитного и электрического полей совпадают, поэтому на дрейфовое движение заряженных частиц магнитное поле влиять не будет. Однако электроны и ионы обладают еще тепловой скоростью хаотического движения и скоростью амбиполярной диффузии. [c.84]
Полезно обратить внимание на то, что скорость звука в газе порядка величины средней тепловой скорости молекул. [c.353]
Эта формула применима постольку, поскольку определяемый ею коэффициент поглощения мал должно быть мало относительное убывание амплитуды на расстояниях порядка длины волны (т. е. должно быть ус/ш диссипацию энергии с помощью незатухающего выражения для звуковой волны. Для газов это условие фактически всегда выполнено. Рассмотрим, например, первый член в (79,6). Условие ус/ кинетической теории газов, коэффициент вязкости v газа — порядка величины произведения длины свободного пробега / иа среднюю тепловую скорость молекул последняя совпадает по порядку величины со скоростью звука в газе, так что v 1с. Поэтому имеем [c.424]
Формула (93,12) применима количественно только при достаточно малых разностя.ч pj — р. Однако качественно мы можем применить формулу (93,13) для определения порядка величины ширины ударной волны и в тех случаях, когда разность р 2 Р порядка величины самих давлений pi, рг- Скорость звука в газе — порядка величины тепловой скорости v молекул. Кинематическая лкинетической теории газов, V Iv 1с, гле / — длина свободного пробега молекул. Поэтому а 1/с (оценка члена с теплопроводностью лает то же самое). Наконец, d V/dp )s К/р и pf с- Внося эти выражения в (93,13), получаем [c.493]
Обычная температуропроводность газа—-порядка величины произведения длины свободного пробега молекул на их тепловую скорость, или, что то же, произведения времени свободного пробега Tea на квадрат скорости. Имея в виду, что тепловая скорость молекул совпадает по порядку величины со скоростью звука, найдем [c.664]
В слабых полях t dнапряженности поля, вследствие чего не зависит от S и подвижность. Поскольку концентрация электронов также не зависит от поля, электропроводность является величиной постоянной. [c.256]
По мере увеличения напряженности поля S возрастает скорость дрейфа. Когда становится сравнимой с тепловой скоростью, результирующая скорость начинает зависеть от S. Это приводит к зависимости подвижности и электропроводности от S , т. е. к отклонению от закона Ома. [c.256]
Тепловое движение электронов в проводниках, замыкающих анодную цепь, является одной из причин флуктуаций измеряемого тока (тепловой шум). Металлический проводник характеризуется большой плотностью электронов проводимости и малой длиной их свободного пробега, в них происходит частый обмен энергией между частицами. Поэтому тепловые скорости электронов могут во много раз превосходить их направленную скорость, обусловленную внешним полем. Собственное тепловое движение электронов можно считать не зависящим от приложенного поля. [c.176]
Величину Ui = Кг — V назовем диффузионной или средней тепловой скоростью i-ro компонента. Вектор плотности массового потока i-ro компонента определяется выражением [c.7]
Коэффициенты X и D зависят от физических свойств среды и температуры. Из молекулярной физики известно, что для газов все коэффициенты переноса (ц, к и D) возрастают вместе со средней тепловой скоростью молекул, т. е. с абсолютной температурой среды. [c.14]
Тепловой скоростью называют скорость двин ения молекулы а относительно системы координат, движущейся со среднемассовой скоростью [c.20]
Среднее значение тепловой скорости [c.50]
В отсутствие внешнего поля свободные электроны и дырки находятся в равновесном состоянии и совершают (при температуре ТфО К) хаотическое движение в объеме полупроводника, средняя тепловая скорость носителей заряда и велика (например, при Т = 300 К1) м/с). [c.59]
Установим физический смысл отношения а/тд. Если бы потенциальный барьер между атомами решетки отсутствовал (f7 = 0) и около атомов всегда сушествовали вакансии, так чтобы на их образование не требовалось затрачивать энергию (f/ш = 0), то атомы двигались бы в решетке со средней тепловой скоростью Vq У /гТ/т 10 м/с подобно молекулам газа. Из (1.14) следует, что при U = = О, [c.25]
Действительно, в уравнении Больцмана приравниваются две операции над функцией распределения молекул по тепловым скоростям. С помощью первой операции подсчитывается за единицу времени изменение функции по времени, координатам и скоростям. Если принять массы всех молекул равными, то это изменение можно записать так [c.37]
Изучим м( тод Чепмена—Энскога на примере решгния этого уравнения. Введем характерные масштабы процессов. Пусть Тг — характерное гидродинамическое времн течения — характерная длина dgl, — характерные линейные размеры упругого и неупругого столкновения соответственно. Вообще говоря, скорости упругих и неупругих процессов могут различаться, что приводит к целому спектру характерных масштабов Однако мы будем предполагать здесь, что неупругим процессам можно сопоставить один характерный линейный масштаб Если частицы не стишком сильно различаются по массам и отсутствуют сильные внешние поля, влияющие на движение заряженных чгстиц в смеси газов, то можно использовать и один масштаб скорости V — среднюю тепловую скорость молекул. [c.104]
Цянь-Сюэ-Сэнь выделяет различные режимы теченгй, основываясь на значениях числа Кнудсена Кп = где I — длина свободного пробега молекул, а — характерный размер области течения. Используя выражение (2.6.12) для средней тепловой скорости и (3.2.13) для т], получаем следующее выражение для числа Кнудсена [c.201]
Для большинства чистых металлов распространение теила, обуслоп.лсннос колебаниями решетки, можно считать пренебрежимо малым по сраниению е переносом. за счет движения свободных электронов. Тепловая скорость движения этих электронов очень велика. Поэтому металлы являются лучшими проводниками тепла по сравнению с другими телами. Различные металлы различно проводят тепло. [c.30]
Если изменение абсолютного значения скорости свободного носителя заряда за счет внешнего поля на среднем пути между соударениями сравнимо с тепловой скоростью, то подвижность носителей заряда будет зависеть от электрического поля, причем она может как увеличиваться, так и уменьшаться в зависимости от температу-окружаю1цей среды. [c.274]
Зависимость проводимости от напряженности поля. При возрастании напряженности поля проводимость остается (рис. 13.2, б) неизменной только в области слабых полей. Это такие значения Е добавочная скорость электрона, сообщаемая полем, мала по сравнению с его тепловой скоростью. При более сильных полях (участок 2) увеличивается вероятность теплового розбуждення электронов и -проводимость начинает возрастать по закону Пуля [c.175]
Впоследствии был разработан метод, получивший название нулевого основанный на том, что при переходе от слабого к сильному полю отдельные подуровни могут пересекаться и поэтому регистрируемая приемником интенсивность пучка дает при возрастании поля максимумы. Таким образом, по отклонению атомных пучков в неоднородном магнитном поле оказалось возможным определить значение ядерных моментов / и величину расщепления нормального терма — последнюю в некоторых случаях с точностью, превышающей спектроскопическую. Это обусловлено тем, что флуктуации тепловых скоростей в меньшей степени влияют на резкость атомных пучков, чем на резкость спектральных линий, так как с увеличением температуры возрастает скорость частиц v и, следовательно, уменьшается время их пролета в поле i ]. [c.567]
Поток г ара, проходящий через внешнюю границу кнудсеновского слоя по направлению к по1верхности жидкости, равен ГППяСуа, от жидкости В пар — тПпочСуаон, где iy — нормальная к поверхности жидкости составляющая средней тепловой скорости молекул п — счетная концентрация молекул, м т — масса молекулы. Результирующий по. ок массы /, отнесенный к единице поверхности, можно представить в первом приб ижении в виде [c.19]
Если через Wix, ly, Wn, обозначить компоненты скорогти молекул первого типа, а через W y, —молекул второго типа до столкновения их, то меру вероятности их сближения можно будет положить равной Индексы указывают, от каких компонент тепловых скоростей следует брать функцию распределения. [c.37]
Представим, что газ, определяемый (1-5-57) — равновесный, но его статистическое состояние неизотропно, т. е. тепловые скорости аюмов или молекул [c.42]
Скорость звука в газах имеет п )имерно тот же порядок, что и средняя тепловая скорость молекул. [c.252]
mash-xxl.info
Скорость средняя тепловая – Энциклопедия по машиностроению XXL
Полагаем, что движение электрона, как частицы с массой Ше и зарядом е, под действием поля Е и ускоряющей силы еЕ происходит в течение времени т = “к/, где v — средняя квадратичная скорость электрона (тепловая, так как скоростью дрейфа пренебрегаем из-за сравнительной малости), а “к — средняя длина свободного пробега электрона (пробег). Движение с ускорением еЕ/т за время т разгонит электрон до скорости дрейфа [c.33]Полезно обратить внимание на то, что скорость звука в газе порядка величины средней тепловой скорости молекул. [c.353]
Эта формула применима постольку, поскольку определяемый ею коэффициент поглощения мал должно быть мало относительное убывание амплитуды на расстояниях порядка длины волны (т. е. должно быть ус/ш диссипацию энергии с помощью незатухающего выражения для звуковой волны. Для газов это условие фактически всегда выполнено. Рассмотрим, например, первый член в (79,6). Условие ус/ кинетической теории газов, коэффициент вязкости v газа — порядка величины произведения длины свободного пробега / иа среднюю тепловую скорость молекул последняя совпадает по порядку величины со скоростью звука в газе, так что v 1с. Поэтому имеем [c.424]
При этом в связи с малостью среднего свободного пути для тепловых нейтронов выполняется условие применимости диффузионного приближения — малость изменения плотности нейтронов на протяжении Is. Наконец, скорость движения тепловых нейтронов можно считать постоянной [c.312]
Величину Ui = Кг — V назовем диффузионной или средней тепловой скоростью i-ro компонента. Вектор плотности массового потока i-ro компонента определяется выражением [c.7]
Коэффициенты X и D зависят от физических свойств среды и температуры. Из молекулярной физики известно, что для газов все коэффициенты переноса (ц, к и D) возрастают вместе со средней тепловой скоростью молекул, т. е. с абсолютной температурой среды. [c.14]
По определению средней тепловой (диффузионной) скорости имеем [c.117]
В отсутствие внешнего поля свободные электроны и дырки находятся в равновесном состоянии и совершают (при температуре ТфО К) хаотическое движение в объеме полупроводника, средняя тепловая скорость носителей заряда и велика (например, при Т = 300 К1) м/с). [c.59]
Процессы средней скорости (например, тепловые деформации), как правило, характеризуются случайными величинами и функциями, что связано с многообразием параметров, определяющих протекание данного процесса. [c.35]
Установим физический смысл отношения а/тд. Если бы потенциальный барьер между атомами решетки отсутствовал (f7 = 0) и около атомов всегда сушествовали вакансии, так чтобы на их образование не требовалось затрачивать энергию (f/ш = 0), то атомы двигались бы в решетке со средней тепловой скоростью Vq У /гТ/т 10 м/с подобно молекулам газа. Из (1.14) следует, что при U = = О, [c.25]
Здесь число Ре определено по скорости набегающего потока и наружному диаметру труб, коэффициент теплоотдачи рассчитывается по среднему тепловому потоку и среднему температурному напору. [c.98]
Б указанных формулах q — тепловой источник Ре = 2гф F/a — число Пекле, относится к телу, где скорость перемещения теплового источника И / — коэффициент трения скольжения, — скорость скольжения Р — среднее напряжение сжатия / ф – радиус фактического пятна касания. В случае гладких тел и при упругих деформациях в контакте вместо г ф следует подставлять полуширину площади касания (по Герцу) для тел с начальным касанием по линии и радиус касания (при круговой площадке контакта) -в случае точечного первоначального касания. Для расчета температурной вспышки в контакте твердых тел можно воспользоваться полученными зависимостями и граничными условиями. В случае движения теплового источника относительно тел с малыми скоростями Pei [c.177]
Из соотношения (1) следует, что для постоянства коэффициента теплоотдачи по длине необходимо и достаточно, чтобы на всем рассматриваемом участке отношение скорости изменения тепловой нагрузки по длине к скорости изменения температурного напора сохранялось постоянным. Температура жидкости в этом соотношении — средняя калориметрическая в данном сечении. Связывая ее с нагрузкой уравнением теплового баланса, можно получить дифференциальные уравнения для различных практически важных случаев и проанализировать решения. [c.60]
Методика проведения экспериментов была следующей. При постоянных значениях давления, массовой скорости и средней температуре (или недогреве) жидкости в опытном элементе, изменяя плотность теплового потока в каждом опыте, определяли зависимость гидравлического сопротивления от тепловой нагрузки. От опыта к опыту изменялись значения давления, массовой скорости, средней температуры жидкости, эквивалентного диаметра канала или величины части периметра с основным тепловыделением. [c.44]
Скорость теплоносителя, м/с Температурный напор, С Средний тепловой поток, Вт/м -Ю- [c.9]
Горячие носители — электроны (дырки) полупроводника, средняя юитетическая энергия которых во внешнем электрическом ноле npeubiinaei среднюю тепловую кТ). в Групповая скорость — кваптово-механичсская скорость квазичастицы, равная [c.280]
Изучим м( тод Чепмена—Энскога на примере решгния этого уравнения. Введем характерные масштабы процессов. Пусть Тг — характерное гидродинамическое времн течения — характерная длина dgl, — характерные линейные размеры упругого и неупругого столкновения соответственно. Вообще говоря, скорости упругих и неупругих процессов могут различаться, что приводит к целому спектру характерных масштабов Однако мы будем предполагать здесь, что неупругим процессам можно сопоставить один характерный линейный масштаб Если частицы не стишком сильно различаются по массам и отсутствуют сильные внешние поля, влияющие на движение заряженных чгстиц в смеси газов, то можно использовать и один масштаб скорости V — среднюю тепловую скорость молекул. [c.104]
Цянь-Сюэ-Сэнь выделяет различные режимы теченгй, основываясь на значениях числа Кнудсена Кп = где I — длина свободного пробега молекул, а — характерный размер области течения. Используя выражение (2.6.12) для средней тепловой скорости и (3.2.13) для т], получаем следующее выражение для числа Кнудсена [c.201]
Произведем для газов непосредственный статистико-механический расчет, который основан на законе распределения молекул по скоростям их теплового движения (распределение Максвелла — Больцмана), и получим зависимость между средней кинетической энергией молекул газа и температурой [c.212]
В связи с тем что в последующем нас будет интересовать главным образом структура уравнения и влияние на искомую температуру таких параметров, как нагрузки, скорости, коэффициент трения, твердости поверхностей и теплофизические характеристики материалов тел, будем пользоваться средними значениями интенсивности нагрузки на фактическом пятне касания. Так, для фрикционного контакта в случае преобладания пластических деформаций неровностей средний радиус пятна касания (г ф) можно оценить по формуле [8] Гф= (NfP nY /2, где N – нагрузка Рф = сОрР = НВ В – твердость по Бринеллю п – количество пятен, составляющих фактическую площадь касания тел с – коэффициент. Получим уравнения для определения температур при наиболее характерных, малых и больишх скоростях перемещения тепловых источников. Подставляем величину радиуса в формулу, например для определения температурной вспышки при высоких скоростях перемещения тел [c.177]
Поток г ара, проходящий через внешнюю границу кнудсеновского слоя по направлению к по1верхности жидкости, равен ГППяСуа, от жидкости В пар — тПпочСуаон, где iy — нормальная к поверхности жидкости составляющая средней тепловой скорости молекул п — счетная концентрация молекул, м т — масса молекулы. Результирующий по. ок массы /, отнесенный к единице поверхности, можно представить в первом приб ижении в виде [c.19]
Скорость звука в газах имеет п )имерно тот же порядок, что и средняя тепловая скорость молекул. [c.252]
Ралеевская линия рассеянного в газе света уширена из-за связанного с движением частиц доплеровского эффекта. Ушнрение зависит от угла рассеяния 0 и, согласно (4), его величина порядка Део ш(и/с)зт6/2, где V — средняя тепловая скорость молекул. Следует отметить, что спектр рассеянного вперед света не уширен, а ширина спектра, рассеянного назад,— порядка доплеровской ширины атомной линии поглощения. [c.281]
В идеальном газе с = УуР/р — УуДТ/р, где й = = 8,31 Дж/моль-К — универсальная газовая постоянная, Т — абс. темп-ра, р. — молекулярная. масса газа. Это т. н. л а п л а с о в а С. з. В газе она совпадает по порядку величины со средней тепловой скоростью движения молекул. Величину с = УР/р называют ньютоновой С. 3., она определяет С. з. при изотермич. процессе распространения, к-рый может иметь место на очень низких частотах. В большинстве случаев С. з. соответствует лапласову значению. [c.546]
Рассмотрение этого вопроса ограничивается экспериментальными исследованиями гидродинамики дифе-нильной смеси, проведенными на полупромышленных опытных установках. На описанном выше замкнутом контуре с естественной циркуляцией С. М. Лукомским, А. В. Чечеткиным и И. Я. Шерстнееым были проведены опыты о гидродинамике кипяш,ей дифенильной смеси в диапазоне изменений давления пара в системе 3— 8 ага, средних тепловых потоков обогреваемого участка контура 9ср от 28 800 до 98 600 ккал/м” – ч и скоростей циркуляции от 0,15 до 1,8 м1сек. В интервале изменений [c.285]
Но так как тлСт, т. е. средняя скорость молекулы легкого газа при данной температуре будет больше средней скорости молекулы тяжелого газа. По формуле (8.1) средняя скорость с теплового движения молекулы газа, имеющего массу т, может быть выражена так =Y kTlm. При постоянной температуре средняя скорость молекул газа обратно пропорциональна корню квадратному из его молекулярной массы. Например, для азота при 760 мм рт. ст. ( 0,1 МПа) и температуре 20°С (293 К) с=470 м/с, для водорода в тех же условиях 1800 м/с. [c.260]
Здесь йзф — коэффициент аккомодации энергии молекул газа на конкретной поверхности — множитель, зависящий от структуры молекул газа Y = Ср/Сц — отношение изобарной и изохорной теплоемкостей V Т) —средняя тепловая скорость молекул газа. Сомножитель А в (7.33) является геометрическим фактором температурного скачка и равен А = 2/8д -4 = (/ ] + г2)1[г г2 п с121с1 ). [c.423]
Теплопроводность, обусловленная переносом. тепла электронами v.e — tle evH/Ъ, где Се—теплоемкость на один электрон и — средняя тепловая скорость электронов ПеСе=С —электронная доля молекулярной теплоемкости Пе — число электронов в единице объема. [c.281]
mash-xxl.info
ТЕПЛОВАЯ СКОРОСТЬ И СКОРОСТЬ ДРЕЙФА
ПРИНЦИПЫ ЛАЗЕРОВ
Как уже отмечалось в предыдущих разделах, именно электроны ответственны за процессы, происходящие в газовых разрядах. Они получают энергию от приложенного электрического поля, а затем отдают ее или обмениваются ей в следующих процессах.
1. Неупругие столкновения с атомами или молекулами газовой смеси, в результате которых эти частицы либо забрасываются в возбужденные состояния, либо ионизуются. Возбуждение электронным ударом или ударная ионизация являются, пожалуй, наиболее важными процессами с точки зрения накачки лазерных сред, и поэтому подробно рассматриваются здесь.
2. Упругие столкновения с атомами. Если предположить, что атом перед столкновением находится в состоянии покоя (действительно, средняя скорость у атомов много меньше, чем у электронов), то электрон потеряет энергию в результате столкновения. Непосредственное рассмотрение процесса упругого столкновения показывает, что при случайных направлениях рассеяния электронов доля начальной энергии, потерянная ими, в среднем составляет величину 2(т/М), где т — масса электрона, а М — масса атома. Отметим, что из-за малости отношения т/М эта величина очень незначительна (например, т/М = 1,3 • 10-5 для атомов Аг).
3. Электрон-электронные столкновения. Даже в газе с умеренной степенью ионизации частота этих столкновений обычно велика, поскольку обе частицы заряжены и взаимодействуют друг с другом на значительных расстояниях. Более того, поскольку сталкивающиеся частицы имеют одинаковую массу, то обмен энергией при таких столкновениях может быть существенен.
В результате перечисленных столкновительных процессов и вследствие того, что электроны в разряде ускоряются электрическим полем, электронный газ в плазме приобретает некоторое распределение по скоростям. Его можно описать, введя функцию распределения электронов по скоростям /(и*, иу, и2), смысл которой заключается в том, что величина /(их, иу9 и2)с11)хс11)ус1и2 определяет вероятность найти электрон с компонентами скорости, попадающими в объем (1)х(11)у(11)г пространства скоростей вблизи точки иу9 иг). При известной функции распределения можно определить тепловую ско-
Рость электронов как
Где усреднение производится как раз по распределению скоростей. Аналогичным образом, можно определить скорость дрейфа электронов ианп как среднюю скорость вдоль направления поля, т. е.
(6.4.11)
Где ось г выбрана вдоль поля, а усреднение снова производится по распределению скоростей электронов.
Для того чтобы грубо оценить величины как так и сделаем упрощающее предположение, что при каждом столкновении теряется некоторая постоянная часть б кинетической энергии электрона. Тогда первое уравнение
V! s-^drift может быть получено из условия сохранения энергии: средняя энергия, теряемая электроном в единицу времени, должна равняться средней мощности, переданной электрону внешний электрическим полем. Отметим, что средняя кинетическая энергия электрона равна mvfh /2, тогда как средняя частота его столкновений равна vth/l, где I — средняя длина свободного пробега электрона. Таким образом, теряемая электроном в единицу времени средняя энергия составляет &(vth/l)(mv? h /2), и эта величина должна равняться мощности, переданной электрическим полем £, а именно, eЈvdrift. Следовательно,
Рис. 6.24 Определение скорости дрейфа, возникающей за счет ускорения электронов внешним электрическим полем между двумя последовательными столкновениями |
Adrift = b(vth /l)(mvfh /2). (6.4.12)
Второе уравнение может быть получено из требования сохранения среднего импульса между двумя последовательными столкновениями. Предположим, что после каждого столкновения электрон рассеивается в произвольном направлении; таким образом, теряется приобретенная скорость дрейфа. В изображении на рис. 6.24 предполагается, что скорость электрона в точке 1, после первого столкновения, имеет величину, равную тепловой скорости vth9 и направление, составляющее некоторый угол 0 с напряженностью поля. За время свободного движения между точками 1 и 2 электрон ускоряется электрическим полем. К следующему столкновению в точке 2 он приобретет дополнительную скорость вдоль поля, в направлении, противоположном вектору напряженности; предположим, что величина этой скорости равна vdrift. Импульс, переданный электрону соответствующей силой, будет равен – eЈl/vth, где I — расстояние между точками 1 и 2 (которое в среднем предполагается равным средней длине свободного пробега электрона). Этот импульс можно теперь приравнять изменению импульса, т. е. разности (mvr – mvth) = mvdrift. Для амплитуд импульсов можно тогда записать уравнение
EЈl = mvthvdrift, (6.4.13)
Которое вместе с уравнением (6.4.12) и составляет искомую пару. Из этих уравнений находим:
Vth = {2/3)1^(е£1/т)1/2 (6.4.14)
Vdrift = (S/2)1/4(eЈ7/m)1/2. (6.4.15)
Отметим, что, используя отношение левых и правых частей (6.4.15) и (6.4.14), можно получить:
(vdrift/vth) = ($/2)1/2. (6.4.16)
Ранее уже отмечалось, что после упругого столкновения с атомом электрон теряет долю своей кинетической энергии, в среднем равную 2(т/М). Если теперь предположить, что 8 = 2(т/М)9 то из (6.4.16) получим, что (vdrift/vth) = (rn/M)1/2 = 10~2. Таким образом, скорость дрейфа составляет весь
ма малую долю тепловой скорости, так что движение электронов в газе можно рассматривать скорее как медленно дрейфующее облако хаотически движущихся частиц, чем как поток частиц.
Соотношение (6.4.16) является достаточно грубым, поскольку его вывод предполагает, что электроны при каждом столкновении теряют постоянную долю б своей энергии. Хотя это и справедливо для упругих столкновений с атомами, очевидно, что такое предположение не подходит для неупругих столкновений, в которых потери энергии сравнимы с энергией возбуждения атомов. Отметим, что хотя упругие столкновения обычно происходят более часто, чем неупругие, однако энергия, теряемая электроном в результате упругого столкновения, очень мала. Таким образом, если бы упругие столкновения были доминирующим процессом, то разряд не являлся бы особо эффективным способом накачки активной среды лазеров; большая часть вложенной в разряд энергии уходила бы фактически на нагрев атомов, а не на возбуждение их переходов. Отметим также, что электрон-электронные столкновения не дают вклад в уравнение баланса энергии (6.4.12), поскольку они просто перераспределяют скорости электронов, не изменяя их средней энергии.
Гравировка по металлу проводится на профессиональном оборудовании. Гравировка с высокой детализацией применяется для оформления подарков, памятных вещей.
В данном разделе приводится краткое описание когерентных свойств света, который излучается обычной лампой (лампой накаливания или газонаполненной лампой). Поскольку свет в этом случае обусловлен спонтанным излучением многих атомов, по существу …
В результате соударений частиц с электронами в объеме электрического разряда происходит постоянное образование электронов и ионов. Ударная ионизация осуществляется присутствующими в разряде горячими электронами, т. е. теми, энергия которых больше …
msd.com.ua
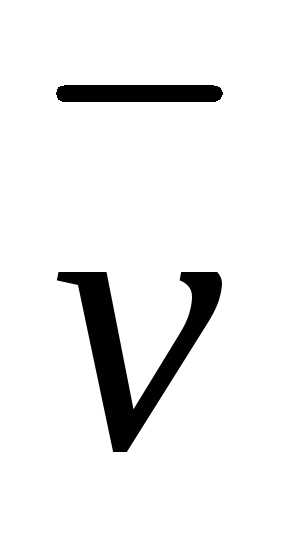 ,
м/с
,
м/с , м/с
, м/с