Учебник по термодинамике – Термодинамика, Новиков И.И., 1984

учебник по термодинамике и молекулярной : Физика

malykh89 писал(а):

вуз уровня МГУ, МФТИ. классические учебники имеют св-во устаревать. вот, к примеру, мне гораздо больше нравится учебник МГУ по механике Диденко, вышедший не так давно, чем книга Сивухина по этой теме.

И имеют, и не имеют. Смотря какие учебники. Просто иногда бывает настолько ценен сам стиль, что ну никак нельзя от такого учебника отказаться. Яркий пример – учебник Ландсберга по оптике (извините, что не в ту степь, но уж очень яркий пример). Ну нет таких учебников больше. Хотя, конечно, по содержанию-то он устарел – последняя модернизация была в 1976 году, а прижизненная так вообще в 50-х, если мне память не изменяет. Вот современный учебник по физической оптике, который был выпущен в серии “Классический учебник МГУ” ну такое убожество. Или вот никто не может отказаться от Борна и Вольфа. Хотя тоже старая книжка

Насчет учебников Сивухина могу сказать следующее. Математика у него простовата. Часто он вообще ограничивается разбором частных случаев (в том числе и с физической точки зрения), а затем, вроде как, перекидывает все это на общий. Но я не могу сказать, что его учебник по т/д и МФ мне не нравится – достаточно обстоятельная книга с физической точки зрения. Берклиевский курс вам тем более не понравится, ибо а) очень старый и б) маловато математики будет.

Есть еще разные спец. книги, но я думаю, что за них браться на начальных этапах совсем не стоит.

malykh89 писал(а):

Хорошо бы и сматематической, и с физической, поскольку для того, чтобы решать задачи надо понимать физику процесса для начала, потом уже – умение применять формулы

Согласен с вами. По-моему курс А.Н.Матвеева будет очень даже ничего для вас. Недавно как раз переиздали его молекулярную физику. Только, наверное, тут нужно дополнение вроде того же Сивухина, т.к. Матвеев имеет особенность затягивать в математическую сторону, что для физика не всегда хорошо. У него вообще такой курс с прицелом на теоретическую физику, в принципе. Очень глубокий и очень солидный.

ing писал(а):

Я много чего не знаю, но пусть это вас не беспокоит.

Это я уже понял по теме про скачки уплотнения, в которой вы так и не осилили правильного написания слова скачок . Так что уже давно не беспокоюсь.

ing писал(а):

быть может сервер на ночь выключают7

Я еще днем пробовал. Если выключают, то на выходные и причем часов в 12 в пятницу

dxdy.ru

Учебное пособие по термодинамике – fiziku5.ru

Введение

Термодинамика является научным фундаментом энергетики, в том числе всех типов поршневых и реактивных двигателей, паровых и газовых турбин. Она является одной из базовых дисциплин при подготовке специалистов в различных областях техники и, прежде всего, в области авиационных и ракетных двигателей.

Термодинамика – это наука об энергии и ее свойствах, наука о взаимопревращениях различных видов энергии (тепловой, механической, химической и др.). Для ее изучения необходимы знания математики, физики и химии.

Термодинамика базируется на трех основных законах термодинамики.

Первый закон термодинамики – это закон сохранения и превращения энергии применительно к термодинамическим процессам.

Второй закон термодинамики характеризует направление протекания реальных термодинамических процессов и условия превращения теплоты в работу. Он состоит из двух принципов: существования энтропии и ее возрастания. Все реальные процессы направлены в сторону возрастания энтропии.

Превращение теплоты в работу возможно только при наличии в ТС двух источников теплоты с различной температурой (горячего и холодного тел), причем вся подведенная теплота не может быть превращена в работу. Часть теплоты должна быть отдана холодному телу.

Третий закон термодинамики объясняет поведение термодинамических систем при абсолютной температуре, стремящейся к нулю (Т→ОК), и может быть сформулирован как принцип недостижимости абсолютного нуля температур (Нернст, 1906год). Согласно этому закону при Т→ОК равновесные процессы идут без изменения энтропии (∆

S→0), а энтропия конденсированных веществ стремится к постоянному значению S→S0=const (Планк предложил считать S0=0). Третий закон термодинамики позволяет найти энтропийные и химические константы веществ, участвующих в химических реакциях.

Термодинамика изучает общие свойства равновесных физических систем на базе трех законов термодинамики и не использует в явном виде представления о молекулярном строении вещества. В термодинамике используется феноменологический (макрофизический) метод изучения равновесных физических систем. Результаты, полученные этим методом, могут обосновываться с помощью молекулярно-кинетической теории, которая опирается на молекулярные представления о строении физических систем, применяя методы математической теории вероятностей. Таким образом, термодинамика и статистическая физика, как науки о свойствах вещества и энергии взаимно дополняют друг друга.

Условно термодинамика подразделяется на техническую термодинамику, изучающую законы взаимопревращения теплоты и механической работы применительно к тепловым двигателям и машинам, химическую термодинамику, изучающую законы взаимопревращения различных видов энергии при изменении химического состава тел, участвующих в процессах обмена энергией, и физическую (общую) термодинамику, изучающую свойства твердых, жидких и газообразных тел, электрические и магнитные явления и излучение на основе общих термодинамических положений.

Особенностью данного курса лекций является изложение перечисленных разделов как единого целого под общим названием: «Термодинамика»

Методы термодинамики применимы только к термодинамическим системам, состоящим из большого числа частиц, что является нижней границей размеров системы, и не применимы к системам бесконечных размеров, например, к Вселенной, что является верхней границей размеров термодинамической системы, т. е. исходные положения термодинамики устанавливаются для термодинамических систем конечных размеров с большим числом частиц.

При решении физических задач в термодинамике нами будут применяться два метода исследования: метод круговых процессов и метод термодинамических потенциалов. Метод круговых процессов состоит в том, что для изучения какого-либо явления подбирается подходящий обратимый цикл, к которому применяются 1-ый и 2-ой законы термодинамики и определяются величины, входящие в эти законы. Этот метод используется для расчета идеальных циклов поршневых и реактивных двигателей. Метод термодинамических потенциалов базируется на использовании объединенных выражений для 1-го и 2-го законов термодинамики, которые позволяют при определенных условиях сопряжения системы с окружающей средой ввести функции состояния – термодинамические потенциалы, обладающие особыми свойствами. Этот метод используется студентами для расчета термодинамических свойств химически реагирующих систем при переходе их в равновесное состояние в курсовой работе применительно к расчету параметров жидкостного ракетного двигателя.

Исторически термодинамика возникла из потребностей теплотехники. Широкое применение паровой машины привело в начале XIX века к необходимости разработки теоретических основ для расчета тепловых машин и повышения их коэффициента полезного действия. Такое исследование было выполнено в 1824 году французским инженером Сади Карно (1796-1832) в работе «Размышления о движущей силе огня и о машинах, способных развивать эту силу». На базе этого исследования в последствие был сформулирован 2-ой закон термодинамики.

В 40-х годах XIX века в результате исследований Майера (1842г), Джоуля (1840г.) Гесса (1840г.) и Гельмгольца получил общее признание закон сохранения и превращения энергии. Этот закон является развитием всеобщего закона сохранения движения материи, установленного в 1746г. М. В. Ломоносовым.

На основе этих исследований был установлен тепловой эквивалент работы и окончательно сформулирован 1-ый закон термодинамики или первое начало термодинамики.

В 50-х годах XIX века Томсоном-Кельвиным введено понятие и создана абсолютная термодинамическая шкала температур.

Клаузиусом (1822-1888гг.) введены понятия внутренней энергии и энтропии, получено уравнение первого закона термодинамики и сформулированы принципы существования и возрастания энтропии.

На базе этих работ термодинамика оформилась как научная система, как самостоятельная отрасль науки.

Большой вклад в развитие термодинамики внесли русские ученые:
— М. В. Ломоносов в 1746г. установил законы сохранения вещества и движения материи;

— Д. И. Менделеев в 1861г. установил критическое состояние вещества, при котором поверхностное натяжение стремится к нулю и пропадает различие между свойствами жидкости и пара;

— М. П. Авенариус и др. определили критические параметры различных веществ. В конце XIX века созданы теория истечения жидкостей и газов, теория паровых машин и двигателей внутреннего сгорания. Развитие термодинамики продолжается в направлении изыскания методов и путей повышения интенсивности и экономичности двигателей и энергетических установок.

Глава 1. Основные понятия и определения термодинамики

1.1.  Формы движения материи, виды энергии, работа и теплообмен

В природе существуют различные формы движения материи: механическая, тепловая, химическая, электрическая, магнитная и др. Так, механическая форма движения состоит в изменении пространственного расположения макроскопических тел, а тепловая форма движения представляет собой хаотическое механическое движение большой совокупности микрочастиц, составляющих макроскопические тела. При передаче движения от одних тел к другим уменьшение движения рассматриваемой формы в одном теле сопровождается эквивалентным увеличением движения той же или иной формы в другом теле в соответствии с принципами сохранения и превращения движения. В случае изменения формы движения наблюдается их количественная эквивалентность. Количественной мерой для всех форм движения материи, способных превращаться одна в другую, является энергия. В природе существует множество видов энергии: кинетическая, химическая, тепловая, гравитационная, электрическая и др. При передаче движения материи с превращением его форм энергия не может быть ни уничтожена, ни создана. Передача движения и энергии от одних тел к другим телам происходит в результате взаимодействия этих тел. Современная физика различает четыре основных вида взаимодействия между элементарными частицами:

— сильное (ядерные реакции) с радиусом взаимодействия 10-13см;

— электромагнитное;

— гравитационное;

— слабое (с радиусом взаимодействия ~2×10-16см).

На микроскопическом уровне проявляются лишь электромагнитные взаимодействия, которые имеют разнообразные проявления для различных макропроцессов. Так, если явления упругости связаны с взаимодействием между одноименно заряженными электронными оболочками соседних атомов твердого тела, то электромагнитное излучение нагретого тела связано с электромагнитным взаимодействием между ядрами и электронными оболочками. Что касается химических реакций, то они связаны с электромагнитным взаимодействием ядер и электронных оболочек различных химических элементов, участвующих в реакции.

Все виды термодинамического взаимодействия (все способы обмена энергией) можно свести к двум принципиально различным способам: совершению работы и теплообмену.

Работа – это передача энергии в результате макроскопического, упорядоченного, организованного, направленного движения тел. Количество передаваемой при этом энергии называют работой или работой процесса. Работа является функцией процесса, т. к. зависит от пути, по которому шел процесс. Это макроскопическая форма передачи энергии.

Различают следующие виды работ:

— механическая работа, совершаемая механической силой по перемещению тел в пространстве;

— работы немеханического характера (электрическая работа перенесения заряда в электрическом поле, магнитная работа, химическая работа и др.).

Теплообмен – это передача энергии под воздействием хаотического, теплового движения микрочастиц, составляющих макроскопические тела, при наличии разности температур соприкасающихся тел. В этом случае количество передаваемой энергии называют теплотой или теплотой процесса. Теплота является функцией процесса, так как зависит от пути процесса. Теплота – это микроскопическая форма передачи энергии.

fiziku5.ru

О построении в учебниках общих курсов по термодинамике

Рассматривая особенности учебников данного периода, следует сказать, что учебник Погодина занимает среди них особое положение в нем общие основы теории термодинамики и другие темы значительно сужены и рассматриваются лишь в той своей части и в том масштабе, которые требуются для изучения тепловых машин. Э о направление в построении курса термодинамики в 20-х — начале 30-х годов получило значительное развитие особенно в небольших учебниках. Оно сохраняется и в настоящее время в учебниках по теплотехнике, в которых в одном из первых разделов приводятся некоторые сведения по термодинамике, необходимые для изложения теплотехники. Стоит также сказать, что в последний год рассматри-вае.мого периода был издан первый небольшой систематический и довольно обстоятельный учебник по технической термодинамике, изложенной без применения высшей математики  [c.96]
В приложении к первой части учебника излагается общая кинетическая теория газов (15 страниц). В этом разделе, построенном на уровне курса физики, рассматриваются вопросы скорость молекул закон Максвелла давление газа законы Авогадро, Гей-Люссака п Дальтона теплоемкость газов число столкновений п средняя свободная длина пути молекул теплопроводность газов внутреннее тре-Н1 е газов величина и число молекул. Принимая во внимание, что курс физики предшествует курсу термодинамики, можно было бы в учебнике по термодина ике этих данных не приводить, тем более в конце учебника.  [c.201]

В некоторых высших школах этот метод получил при.менение и развитие, особенно при создании курсов сравнительно новых научных дисциплин, а также при построении некоторых разделов курса технической термодинамики (например, общая теория водяного пара). Это значительно упрощало учебники и позволяло излагать на лекциях курс термодинамики за. меньшее число часов. Пожалуй, на русском языке первым учебником, в котором был применен этот  [c.222]

Прн такой постановке отпала необходимость изложения в учебниках общей теории дифференциальных уравнений термодинамики и применения основанного на данных этой теории общего термодинамического метода исследования. Это мероприятие, исключавшее из курса термодинамики ценную и принципиальную часть, коренным образом изменяло содержание и построение учебников ио термодинамике. Этот метод построения курса технической термодинамики получил применение и во многих учебниках, изданных в 20—30-х годах.  [c.223]

Как видим, в учебнике отсутствуют общая теория дифференциальных уравнений термодинамики и обилие следствия ее. Это обстоятельство определяет особенности построения и изложения в учебнике курса термодинамики.  [c.230]

Переходя к общему построению учебников, которое обеспечивает в них последовательное развитие теории, надо сказать, что эта задача в отдельных учебниках разрешается различно, что и создает их индивидуальные особенности. В этой части в учебниках не может быть единства, да и стремление к нему было бы неправильным, так как в построении учебников в целом и нх отдельных частей отражаются понимания автора и его опыт, накопленный в результате преподавания термодинамики. Анализ структуры существующих учебников убеждает в том, что одни и те же разделы курса излагаются в них очень разнообразно.  [c.290]

Значительно влияет на построение всего курса термодинамики расположение в нем разделов, посвященных первому и второму законам термодинамики. Во многих учебниках, в том числе и в большинстве классических, особенно по общей термодинамике, первый и второй законы рассматриваются в начале учебника, а затем уже рассматривается общая теория термодинамики. Подобное построение курса имеет многие положительные особенности.  [c.293]

Третье издание учебника имеет следующее построение курса. Часть первая Основные законы термодинамики . Гл, 1 Введение гл, 2 Первое начало термодинамики гл. 3 Второе начало термодинамики (сущность второго начала термодинамики интегрирующий делитель для выражения элементарного количества тепла энтропия аналитическое выражение второго начала термодинамики полезная внешняя работа термодинамические потенциалы и характеристические функции тепловая теорема Нернста дифференциальные уравнения термодинамики в частных производных статистическое толкование второго начала термодинамики) гл. 4 Термодинамическое равновесие гл. 5 Термодинамические процессы гл. 6 Газы и их смеси гл. 7 Насыщенные влажные и перегретые пары гл. 8 Течение газов и паров гл. 9 Общий термодинамический метод анализа циклов тепловых двигателей . Часть вторая Рабочие циклы тепловых двигателей . Гл. 10 Сжатие газов и паров гл. 11 Циклы поршневых двигателей внутреннего сгорания гл. 12 Циклы газотурбинных установок и реактивных двигателей гл. 13 Циклы паросиловых установок гл. 14 Циклы холодильных машин гл. 15 Термодинамические принципы получения теплоты гл. 16 Термодинамика химических реакций .  [c.349]

Заметим, что учебник Грузинцева после учебников Радцига п Саткевича является третьим чебником, в котором общим вопросам методики тер.модинамики было уделено большое внимание. Надо сказать, что эти вопросы в учебниках XIX столетия не ставились и открыто в них о методике построения курса термодинамики и его изложения не говорилось, и только в начале XX столетия в учебнике Радцига, а затем в учебниках Саткевича и Грузинцева впервые появились такие выражения, как метод доказательства , метод обоснования, метод построения и пр. В постановке вопросов методики и отведении им при построении и изложении курса термодинамики большого значения состоит огромная заслуга авторов этих учебников. Радциг, Саткевич и Грузинцев, можно сказать, являются пионерами в постановке в учебниках вопросов методики термодинамики. Их благотворное начало в последующие годы и особенно после Великой Социалистической октябрьской революции получило огромное развитие.  [c.155]

Из этих учебников особенно яркими по своему содержанию, построению и методам изложения являются учебники Радцига, Мерцалова, Грузинцева и Брандта. Это лучшие учебники по термодинамике начала XX в. В учебнике Грузинцева были блестяще изложены основы теории термодинамики и их приложение к исследованию некоторых физических и химических процессов, в учебниках же Рад-.цига, Мерцалова и Брандта хорошо изложены общие курсы технической термодинамики, содержавшие тщательно методически отработанные и развитые по своей тематике теоретические основы термодинамики и их приложения к тепловым машинам. Особенно развитой теоретическая часть курса термодинамики была в учебнике Брандта она значительно выходила за рамки теоретической части обычных курсов термодинамики.  [c.97]

К недостаткам книги надо отнести также некоторую многословность изложения, обилие второстепенных данных, перегружающих курс и отвлекающих внимание от основной темы, а также некоторую отвлеченность в постановке и изложении отдельных положений курса, без указания их практического значения. Доказательства п отдельные выводы являются довольно сложными, но это является общим недостатком многих сочинений того времени. Особенно слож-ны.м в учебнике Саткевича являются построение теории дифференциальных уравнений термодинамики и применение их при исследовании отдельных явлений и процессов. К недостаткам учебника приходится отнести также очень бедное графическое оформление в не.м содержится всего 28 рисунков, к тому же очень плохо выполненны.х.  [c.142]

Последние два сочинения являются фундаментальными, современными и тщательно отработанными учебниками, в которых наряду с общим курсом физической химии весьма полно и обстоятельно излагаются начала термодинамики и основные положения ее теории. Лица, интересующиеся термодинамикой и термохимией, найдут в этих двух хорошо написанных учебниках много ценного и интересного как в содержании, построении теории всего курса в целом, а также и отдельных разделов, так и в методах обосновани и доказательств.  [c.338]

---

mash-xxl.info

Молекулярная физика и основы термодинамики электронный учебник по физике кгту-кхти. Кафедра физики. Поливанов М. А., Старостина И. А., Кондратьева О. И – Учебник

МОЛЕКУЛЯРНАЯ ФИЗИКА И ОСНОВЫ ТЕРМОДИНАМИКИ

Электронный учебник по физике

КГТУ-КХТИ. Кафедра физики. Поливанов М.А., Старостина И.А., Кондратьева О.И.

Для перемещения по тексту электронного учебника можно использовать:

1- нажатие клавиш PgDn, PgUp,,  для перемещения по страницам и строкам;

2- нажатие левой клавиши «мыши» по выделенному тексту для перехода в требуемый раздел;

3- нажатие левой клавиши «мыши» по выделенному значку @ для перехода в оглавление.

ОГЛАВЛЕНИЕ

Введение

1. Молекулярно-кинетическая теория идеальных газов

1.1 Термодинамические параметры

1.2. Уравнение состояния идеального газа

1.3. Основное уравнение молекулярно-кинетической теории идеальных газов и его следствия

1.4. Барометрическая формула

1.5. Закон Больцмана о распределении частиц во внешнем потенциальном поле.

1.6.  Распределение Максвелла молекул идеального газа по скоростям

2. Основы термодинамики

2.1. Внутренняя энергия

2.2. Первое начало термодинамики

2.3. Теплоемкость

2.4. Применение первого начала термодинамики к изопроцессам

2.5. Второе начало термодинамики

2.6. Энтропия

3. Явления переноса

3.1. Теплопроводность

3.2. Внутреннее трение (вязкость)

3.3. Диффузия

4. Реальные газы
4.1. Понятие фазы и фазовых переходов

4.2. Уравнение Ван-дер-Ваальса

4.3. Изотермы реальных газов

5. Жидкости

5.1. Свойства и строение жидкостей

5.2. Поверхностное натяжение жидкостей

5.3. Смачивание. Краевой угол

5.4. Поверхностное испарение и кипение жидкостей

5.5. Жидкие растворы

6. Особенности твердого состояния вещества

6.1. Структура твердых тел

6.2. Физические типы кристаллических решеток

6.3. Теплоемкость кристаллов

6.4. Плавление и кристаллизация

ВВЕДЕНИЕ. @

Молекулярная физика – раздел физики, в котором изучаются свойства тел в различных агрегатных состояниях на основе рассмотрения их молекулярного строения. Физические свойства макроскопических систем (т.е. систем, состоящих из очень большого числа частиц) изучаются двумя разными, но взаимно дополняющими друг друга методами – статистическим и термодинамическим.

Статистический метод основан на использовании теории вероятностей. В этом методе свойства макроскопической системы определяются усредненными значениями скорости частиц, их энергии и других динамических характеристик. Например, температура тела определяется скоростью хаотического движения его молекул, но так как в любой момент времени различные молекулы имеют разные скорости, то температура может быть выражена только через среднее значение скорости движения. Нельзя говорить о температуре одной молекулы.

Термодинамический метод основан на анализе законов и условий, характеризующих, происходящие в системе изменения макропараметров типа давления, энергии, энтропии и др. В этом методе не рассматривается внутреннее микроскопическое строение изучаемых тел и их изменения. Раздел теоретической физики, в котором изучаются свойства макроскопических систем и энергетика различных физических и химических процессов, называется термодинамикой. В основе термодинамики лежит несколько фундаментальных законов (начал), которые являются обобщением многочисленных наблюдений.

1.  МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ИДЕАЛЬНЫХ ГАЗОВ

1.1.  Термодинамические параметры. @

Мысленно выделенная макроскопическая система, рассматриваемая методами термодинамики, называется термодинамической системой. Все тела, не включенные в состав исследуемой системы, называются внешней средой. Состояние системы задается термодинамическими параметрами (или, по-другому, параметрами состояния) – совокупностью физических величин, характеризующих свойства системы. Обычно в качестве основных параметров выбирают давление р, температуру Т и удельный объем v. Различают два типа термодинамических параметров: экстенсивные и интенсивные. Экстенсивные параметры пропорциональны количеству вещества в системе, а интенсивные не зависят от количества вещества и массы системы. Интенсивными параметрами являются давление, температура, удельный объем и др., а экстенсивными – объем, энергия, энтропия.

Объем пропорционален количеству вещества в системе. При расчетах удобнее оперировать с удельным объемом v – это величина, равная отношению объема к массе системы, то есть объем единицы массы v = V/m = 1/ρ, где ρ – плотность вещества.

Давлением называется физическая величина 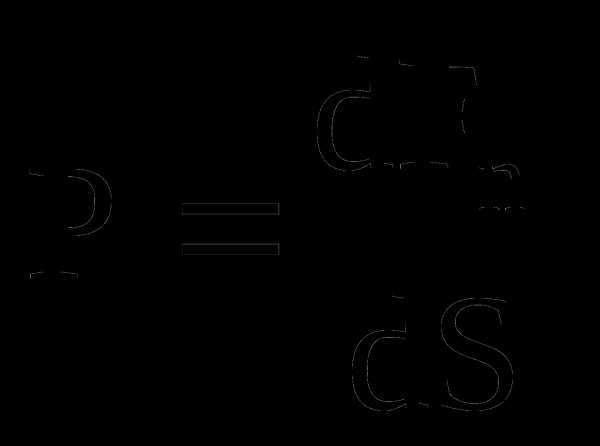где dF_n– проекция силы на нормаль к поверхности площадью_dS.

Температура – это физическая величина, характеризующая энергию макроскопической системы, находящейся в состоянии термодинамического равновесия. Температура системы является мерой интенсивности теплового движения и взаимодействия частиц, образующих систему. В этом состоит молекулярно-кинетический смысл температуры. В настоящее время существует две температурных шкалы – термодинамическая (градуированная в Кельвинах (К)) и Международная практическая (градуированная в градусах Цельсия (˚С)). 1˚С = 1К. Связь между термодинамической температурой Т и температурой по Международной практической шкале имеет вид: Т = t + 273,15˚С.

Всякое изменение состояния термодинамической системы, характеризующееся изменением ее параметров, называется термодинамическим процессом. Термодинамический процесс называется равновесным, если при этом система проходит ряд бесконечно близких равновесных состояний. Равновесное состояние – это такое состояние, в которое система приходит в конце концов при неизменных внешних условиях и дальше остается в этом состоянии сколь угодно долго. Реальный процесс изменения состояния системы будет тем ближе к равновесному, чем медленнее он совершается.

1. 2. Уравнение состояния идеального газа. @

В молекулярно-кинетической теории широко используется физическая модель идеального газа. Это вещество, находящееся в газообразном состоянии, для которого выполняются следующие условия:

1. Собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда.

2. Между молекулами газа отсутствуют взаимодействия, кроме случайных столкновений.

3. Столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.

Модель идеального газа можно использовать при изучении реальных газов, т.к. они при условиях, близких к нормальным (давление р₀ = 1,013∙10⁵Па, температура Т₀=273,15К) ведут себя аналогично идеальному газу. Например, воздух при Т=230К и р= р₀/50 по всем трем критериям подобен модели идеального газа.

Поведение идеальных газов описывается рядом законов.

Закон Авогадро: моли любых газов при одинаковых температуре и давлении занимают одинаковые объемы. При нормальных условиях этот объем равен V_M=22,4∙10^-3м³/моль. В одном моле различных веществ содержится одно и то же число молекул, называемое числом Авогадро N_A= 6,022∙10²³моль^-1 .

Закон Бойля – Мариотта: для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная pV = const при Т = const и m = const.

Закон Шарля: давление данной массы газа при постоянном объеме изменяется линейно с температурой р=р₀(1+αt) при V = const и m = const.

Закон Гей-Люссака: объем данной массы газа при постоянном давлении изменяется линейно с температурой V = V₀(1+αt) при р = const и m = const. В этих уравнениях t – температура по шкале Цельсия, р₀ и_{V0 -давление и объем при 0°С, коэффициент α =1/273,15 К^-1.}

Французский физик и инженер Б.Клапейрон и русский ученый Д.И.Менделеев, объединив закон Авогадро и законы идеальных газов Бойля – Мариотта, Шарля и Гей – Люссака, вывели уравнение состояния идеального газа – уравнение, связывающее вместе все три термодинамических параметра системы: для одного моля газа рV_М= RT и для произвольной массы газа

г
де V_{М –} молярный объем, т.е. объем одного моля газа, R – молярная газовая постоянная, равная 8,31Дж/(моль·К), М – молярная масса, V= V_М· m/M – объем всей массы газа,  = m/M – количество вещества в молях. Это уравнение называется уравнением Менделеева– Клапейрона.

Существует еще одна форма записи данного уравнения:

Е
е можно получить, если учесть, что k =R/N_{A= 1,38∙10^-23 Дж/К – это постоянная Больцмана, а n =NA/VМ – это концентрация молекул газа.}

Для расчета давления в смеси разных газов применяется закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов: р =р₁ + р₂ + … + p_n . Парциальное давление – это такое давление, которое производил бы газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре. Для расчета парциального давления идеального газа используют уравнение Менделеева– Клапейрона.

1. 3. Основное уравнение молекулярно – кинетической теории идеальных газов и его следствия. @

Рассмотрим одноатомный идеальный газ, занимающий некоторый объем V (рис.1.1.) Пусть число столкновений между молекулами пренебрежимо мало по сравнению с числом столкновений со стенками сосуда. В

Рис.1.1. К выводу основного уравнения молекулярно-кине­тической теории.

ыделим на стенке сосуда некоторую элементарную площадку ΔS и вычислим давление, оказываемое на эту площадку. При каждом соударении молекула, массой m₀, движущаяся перпендикулярно площадке со скоростью υ, передает ей импульс, который представляет собой разницу импульсов молекулы до и после соударения:

m₀υ -(-m₀υ) = 2m₀υ.

За время Δt площадки ΔS достигнут только те молекулы, которые заключены в объеме цилиндра с основанием ΔS и длиной υΔt. Это число молекул будет nυΔSΔt, где n – концентрация молекул. Необходимо, однако, учитывать, что реально молекулы движутся к площадке под разными углами и имеют различные скорости, причем скорость молекул при каждом соударении меняется. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных координатных осей, так что в любой момент времени вдоль каждого из них движется 1/3 молекул, причем половина – 1/6 – движется в одну сторону, половина – в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку ΔS будет nυΔSΔt /6. При столкновении с площадкой эти молекулы передадут ей импульс

.

В данном случае, когда сила, действующая на единицу площади, постоянна, для давления газа на стенку сосуда мы можем записать р = F/ΔS = ΔP/ΔSΔt = = nm₀υ²/3. Молекулы в сосуде движутся с самыми различными скоростями υ_1,υ_2….υ_n, общее число их – N. Поэтому необходимо рассматривать среднюю квадратичную скорость, которая характеризует всю совокупность молекул:

Т
аким образом, давление газа, оказываемое им на стенку сосуда, будет равно

П
риведенное выше уравнение и есть основное уравнение молекулярно-кинетической теории идеальных газов. Поскольку m₀‹υ_кв›²/2 – это средняя энергия поступательного движения молекулы ‹ ε_пост›, уравнение можно переписать в виде:

С
ледствия:

1. Учитывая, что концентрация n = N/V, получаем

г
де E – суммарная кинетическая энергия поступательного движения всех молекул газа. Таким образом, давление равно двум третям энергии поступательного движения молекул, содержащихся в единице объема газа.

2. Для вывода второго следствия воспользуемся первым следствием и уравнением Менделеева-Клапейрона:

Энергия молекул Е в веществе пропорциональна количеству вещества в системе и температуре.

4. Н
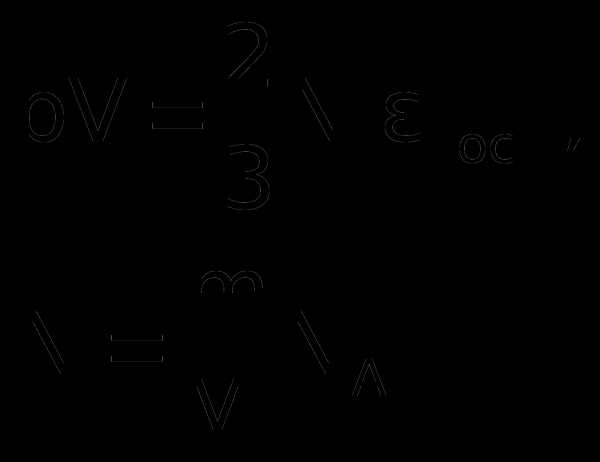
   айдем еще кинетическую энергию поступательного движения одной молекулы ‹ ε_пост›, учитывая

k =R/N_A получим:

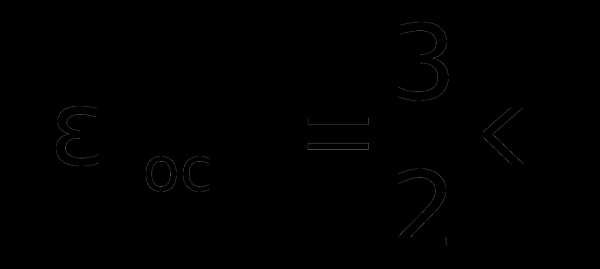
Отсюда следует, что средняя кинетическая энергия хаотического поступательного движения молекул идеального газа пропорциональна его абсолютной температуре и зависит только от нее, т.е. температура есть количественная мера энергии теплового движения молекул. При одинаковой температуре средние кинетические энергии молекул любого газа одинаковы. При Т=0К ‹ε_пост› = 0 и поступательное движение молекул газа прекращается, однако анализ различных процессов показывает, что Т = 0К – недостижимая температура.

4. Учитывая, что  ‹ε_пост› = 3kT/2, р = 2n‹ ε_пост›/3, получим отсюда: р = nkT.

Мы получили уже знакомый нам вариант уравнения Менделеева-Клапейрона, выведенный в данном случае из понятий молекулярно-кинетической теории статистическим методом. Последнее уравнение означает, что при одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул.

1. 4. Барометрическая формула. @

При выводе основного уравнения молекулярно-кинетической теории предполагалось, что если на молекулы газа не действуют внешние силы, то молекулы равномерно распределены по объему. Однако молекулы любого газа находятся в потенциальном поле тяготения Земли. Тяготение, с одной стороны, и тепловое движение молекул, с другой, приводят к некоторому стационарному состоянию газа, при котором концентрация молекул газа и его давление с высотой убывают. Выведем закон изменения давления газа с высотой, предполагая при этом, что поле тяготения однородно, температура постоянна и масса всех молекул одинакова. Если атмосферное давление на высоте h равно р, то на высоте h+dh оно равно р + dp (рис.1.2). При dh > 0, dр < 0, т.к. давление с высотой убывает. Разность давлений р и (р + dр) равна гидростатическому давлению столба газа авсd, заключенного в объеме цилиндра высотой dh и площадью с основанием равным единице. Это запишется в следующем виде: p- (p+dp) = gρdh, – dp = gρdh или dp =  gρdh, где ρ – плотность газа на высоте h. Воспользуемся уравнением состояния идеального газа рV = mRT/M и выразим плотность ρ=m/V=pM/RT. Подставим это выражение в формулу для dр:

dp = – pMgdh/RT или dp/p = – Mgdh/RT

Интегрирование данного уравнения дает следующий результат: Здесь С – константа и в данном случае удобно обозначить постоянную интегрирования через lnC. Потенцируя полученное выражение, находим, что

При условии h=0 получим, что С=р₀, где р₀-давление на высоте h=0.

Д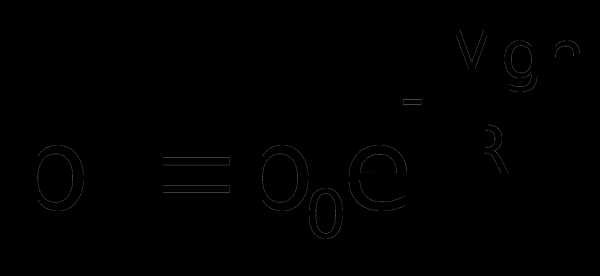
анное выражение называется барометрической формулой. Она позволяет найти атмосферное давление в зависимости от высоты, или высоту, если известно давление.

Зависимость давления от высоты демонстрирует рисунок 1.3. Прибор для определения высоты над уровнем моря называется высотомером или альтиметром. Он представляет собой барометр, проградуированный в значениях высоты.

1. 5. Закон Больцмана о распределении частиц во внешнем потенциальном поле. @

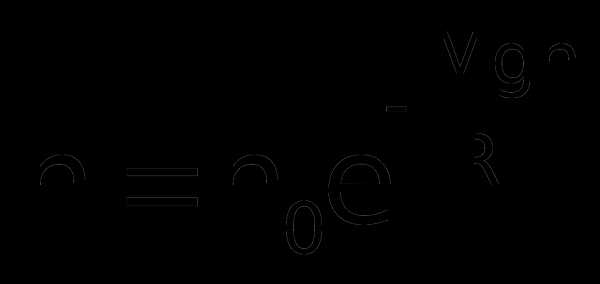
Если воспользоваться выражением р = nkT, то можно привести барометрическую формулу к виду:

з
десь n – концентрация молекул на высоте h, n₀ – то же у поверхности Земли. Так как М = m₀N_{A, где m0 – масса одной молекулы, а R = k NA, то мы получим П = m0gh – это потенциальная энергия одной молекулы в поле тяготения. Поскольку kT~‹εпост›, то концентрация молекул на определенной высоте зависит от соотношения П и ‹εпост›}

Полученное выражение называется распределением Больцмана для внешнего потенциального поля. Из него следует, что при постоянной температуре плотность газа (с которой связана концентрация) больше там, где меньше потенциальная энергия его молекул.

1. 6. Распределение Максвелла молекул идеального газа по скоростям. @

При выводе основного уравнения молекулярно-кинетической теории отмечалось, что молекулы имеют различные скорости. В результате многократных соударений скорость каждой молекулы меняется со временем по модулю и по направлению. Из-за хаотичности теплового движения молекул все направления являются равновероятными, а средняя квадратичная скорость остается постоянной. Мы можем записать

П
остоянство ‹υ_кв› объясняется тем, что в газе устанавливается стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется определенному статистическому закону. Этот закон теоретически был выведен Д.К.Максвеллом. Он рассчитал функцию f(), называемую функцией распределения молекул по скоростям. Если разбить диапазон всех возможных скоростей молекул на малые интервалы, равные d, то на каждый интервал скорости будет приходиться некоторое число молекул dN(), имеющих скорость, заключенную в этом интервале (Рис.1.4.).

Функция f(v) определяет относительное число молекул, скорости которых лежат в интервале от  до + d. Это число – dN()/N= f()d. Применяя методы теории вероятностей, Максвелл нашел вид для функции f()

Д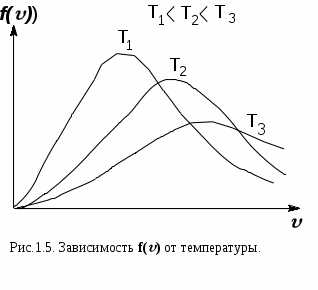анное выражение – это закон о распределении молекул идеального газа по скоростям. Конкретный вид функции зависит от рода газа, массы его молекул и температуры (рис.1.5). Функция f()=0 при =0 и достигает максимума при некотором значении _в, а затем асимптотически стремится к нулю. Кривая несимметрична относительно максимума. Относительное число молекул dN()/N, скорости которых лежат в интервале d и равное f()d, находится как площадь заштрихованной полоски основанием dv и высотой f(), показанной на рис.1.4. Вся площадь, ограниченная кривой f() и осью абсцисс равна единице, потому что, если просуммировать все доли молекул, имеющих всевозможные значения скорости, то получается единица. Как показано на рис.1.5, с ростом температуры кривая распределения смещается вправо, т.е. растет число быстрых молекул, но площадь под кривой остается постоянной, т.к. N = const.

Скорость _в, при которой функция f() достигает максимума, называется наиболее вероятной скоростью. Из условия равенства нулю первой производной функции f(v) ′ = 0 следует, что

Н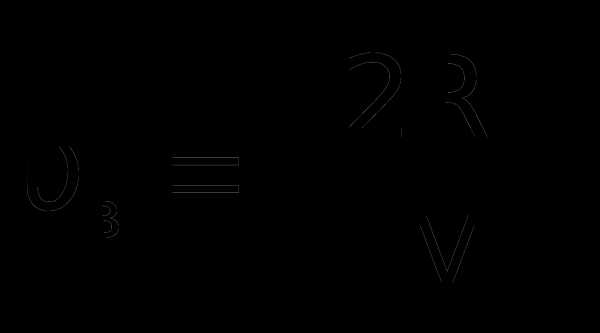
а рисунке 1.4. отмечена еще одна характеристика – средняя арифметическая скорость молекулы. Она определяется по формуле:

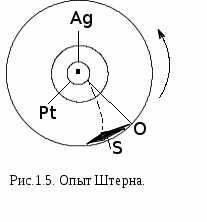Опыт, проведенный немецким физиком О.Штерном, экспериментально подтвердил справедливость распределения Максвелла (рисунок 1.5.). Прибор Штерна состоит из двух коаксиальных цилиндров. Вдоль оси внутреннего цилиндра со щелью проходит платиновая проволока, покрытая слоем серебра. Если пропустить по проволоке ток,она нагревается и серебро испаряется. Атомы серебра, вылетая через щель, попадают на внутреннюю поверхность второго цилиндра. Если прибор будет вращаться, то атомы серебра осядут не против щели, а сместятся от точки О на некоторое расстояние. Исследование количество осадка позволяет оценить распределение молекул по скоростям. Оказалось, что распределение соответствует максвелловскому.

2. ОСНОВЫ ТЕРМОДИНАМИКИ

2.1. Внутренняя энергия. @

Важной характеристикой любой термодинамической системы является ее внутренняя энергия – энергия хаотического теплового движения частиц системы – молекул, атомов и энергия их взаимодействия. К внутренней энергии не относится кинетическая энергия движения системы как целого и потенциальная энергия системы во внешних полях. Внутренняя энергия системы в определенном состоянии не зависит от того, как система пришла в это состояние (т.е. от пути перехода), а определяется только значениями термодинамических параметров в этих состояниях. В термодинамике имеются и другие функции, удовлетворяющие этим условиям, их называют функциями состояния системы. Таким образом, внутренняя энергия – это функция состояния.

Для дальнейших рассуждений нам понадобится понятие числа степеней свободы – это число независимых переменных (координат), полностью определяющих положение системы в пространстве. Например, молекулу одноатомного газа можно рассматривать как материальную точку, обладающую тремя степенями свободы поступательного движения (координаты x,y,z) (рис.2.1. а). Молекула двухатомного газа, рассматриваемая в классической механике как совокупность двух материальных точек, жестко связанных между собой, имеет уже 5 степеней свободы. У нее имеется 3 степени свободы поступательного движения центра масс и 2 степени вращательного, связанного с поворотами на углы  и  (рис. 2.1. б). Эти углы   полярный угол θ и азимутальный угол φ, определяют ориентацию оси молекулы. В данном случае, на первый взгляд кажется, что необходимо также задавать угол поворота ψ молекулы относительно собственной оси. Но вращение двухатомной молекулы вокруг своей собственной оси ничего не меняет в положении молекулы, так как структуры у материальных точек атомов нет и, поэтому, этот угол не нужен для задания положения такой молекулы в пространстве. Трехатомные молекулы (рис. 2.1.в), в которых атомы связаны жестко между собой, имеют 6 степеней свободы, так как здесь уже необходим дополнительный угол ψ.

Если расстояния между атомами меняются, т.е. атомы в молекуле колеблются, то для задания этих расстояний необходимы дополнительные координаты – колебательные степени свободы и общее число степеней свободы будет больше 6. Для много-атомных молекул число степеней может быть намного больше 6.

Р

Рис.2.1. Степени свободы: а) одноатомной молекулы;б) двухатомной молекулы;в) трех- и многоатомной молекулы.

анее мы получили формулу для средней кинетической энергии поступательного движения одно-атомной молекулы идеального газа следующее выражение: ‹ε₀› = 3kT/2. Но у одно-атомной молекулы имеется 3 степени свободы поступательного движения и ни одна не имеет преимущества перед другими. Поэтому на каждую степень в среднем должна приходиться одинаковая энергия, равная 1/3 общей: ‹ε₁› = kT/2. Так как, очевидно, что все степени свободы равноценны, то в классической статистической физике существует закон Больцмана о равномерном распределении энергии по степеням свободы. Он формулируется так: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная кТ/2, а на каждую колебательную степень свободы – кТ. Колебательная степень свободы обладает вдвое большей энергией, так как на нее приходится не только кинетическая, но и потенциальная энергия взаимодействия. Таким образом, средняя энергия любой молекулы ‹ε› = ikT/2, где i – это сумма поступательных, вращательных и удвоенного числа колебательных степеней свободы.

Из этого закона получаем, что внутренняя энергия U_М одного моля идеального газа равна U_М=ikTN_A/2 = iRT/2, а внутренняя энергия U газа массы m равна U = ikTN/2 = iRTm/2M (здесь мы учитываем, что потенциальная энергия взаимодействия молекул равна 0, общее число молекул в одном моле равно N_A, N= mN_A/M и kN_A=R).

2.2.  Первое начало термодинамики. @

Обмен энергией между термодинамической системой и внешней средой может осуществляться двумя качественно различными способами: путем совершения работы и путем теплообмена.

Изменение энергии системы, происходящее под действием сил измеряется работой. Если термодинамическая система совершает работу против внешних сил, то работа считается положительной (А>0). Если работу над системой совершают внешние силы, то она считается отрицательной (А< 0).

Изменение энергии системы, происходящее в результате теплообмена, определяется количеством переданной или отнятой теплоты Q. При теплообмене тела систем должны находится в тепловом контакте, т.е. молекулы этих систем должны иметь возможность сталкиваться при своем движении и обмениваться своей кинетической энергией. Если энергия (теплота) передается системе, то Q>0, если она от системы отнимается, то Q<0. Итак, работа и теплота – это две формы передачи энергии от одних тел другим. Поскольку внутренняя энергия – это механическая энергия всех молекул, то при всех ее изменениях должен соблюдаться закон сохранения энергии. Применительно к термодинамическим процессам этим законом является первое начало термодинамики, установленное в результате обобщения опытных данных. Опыт показал, что при любом способе перехода системы из состояния 1 в состояние 2 изменение внутренней энергии системы ΔU = U₁ – U₂ определяется количеством теплоты Q, полученной системой, и работой А, совершенной системой против внешних сил (получаемое тепло увеличивает энергию системы, а работа системы над внешней средой уменьшает ее) :

ΔU = Q – A или Q = ΔU + A

В дифференциальной форме (для малых изменений величин) это запишется следующим образом:

refdb.ru