А.А. Мальшин Определение удельной теплоемкости воздуха при постоянном давлении
МИНИСТЕРСТВООБРАЗОВАНИЯРОССИЙСКОЙФЕДЕРАЦИИ ГОСУДАРСТВЕННОЕУЧРЕЖДЕНИЕ
КУЗБАССКИЙГОСУДАРСТВЕННЫЙТЕХНИЧЕСКИЙУНИВЕРСИТЕТ КАФЕДРА ФИЗИКИ
ОПРЕДЕЛЕНИЕ УДЕЛЬНОЙ ТЕПЛОЕМКОСТИ ВОЗДУХА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
Методические указания к лабораторной работе № 303 по курсу общей физики для подготовки студентов по всем направлениям
Составители А. А. Мальшин В. П. Корчуганов
Утверждены на заседании кафедры Протокол №1 от 30.08.01 Рекомендованы к печати методической комиссией направления 550600 Протокол №3 от 2.10.01 Электронная копия находится в
библиотеке главного корпуса ГУ КузГТУ
Кемерово 2002
1
ОПРЕДЕЛЕНИЕ УДЕЛЬНОЙ ТЕПЛОЕМКОСТИ ВОЗДУХА ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
Данная лабораторная работа относится к разделу «Молекулярная физика и термодинамика», тема «Законы термодинамики».
Перед занятием студент обязан самостоятельно подготовиться к лабораторной работе (см. п. 3). На выполнение и защиту данной работы отводится 2 часа аудиторных занятий.
1.ЦЕЛИ РАБОТЫ:
1)освоить принципы определения удельной теплоемкости при постоянном давлении методом протока;
2)определить удельную теплоемкость воздуха при постоянном давлении;
3)изучить методы измерения разности температур и расхода воздуха.
2.ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ:
установка для определения удельной теплоемкости при постоянном давлении.
3.ПОДГОТОВКА К РАБОТЕ:
1)изучить теоретические положения, касающиеся данного явления по литературным источникам [1-3];
2)изучить данные методические указания;
3)ответить на контрольные вопросы на с. 10.
4.ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Передача энергии от одного тела к другому может быть осуществлена двумя способами: первый способ – посредством механического взаимодействия, когда совершается работа; второй способ – посредством теплового взаимодействия, когда энергия передается хаотическим движением молекул за счет теплопроводности или теплового излучения. Количество энергии, передаваемое при тепловом взаимодействии тел, называется количеством теплоты.
Первое начало термодинамики говорит о том, что теплота, сооб-
щаемая телу, расходуется на изменение внутренней энергии системы и на совершение телом работы против внешних сил:
2
Одним из основных тепловых свойств тел, широко используемых в термодинамическом методе исследования, является теплоемкость.
Теплоемкостью тела называется физическая величина, численно равная отношению теплоты, сообщаемой телу, к изменению температуры тела Т в рассматриваемом термодинамическом процессе:
Теплоемкость тела зависит от его химического состава, массы тела и его термодинамического состояния, а также от вида процесса изменения состояния тела, в котором поступает теплота ∂Q.
Тепловые свойства однородных тел характеризуются понятиями удельной Сm и молярной теплоемкости CM
Удельной теплоемкостью называется физическая величина, равная теплоте, необходимой для нагревания одного килограмма вещества на один кельвин:
Cm = m∂dQT,
где m – масса тела.
Молярной теплоемкостью называется ная теплоте, необходимой для нагревания один кельвин:
СM= M ∂Q m d T
физическая величина, раводного моля вещества на
,
где М – молярная масса вещества. Связь между теплоемкостями:
Тогда можно записать количество теплоты в виде:
∂Q= C d T= m Cm d T= Mm CM d T.
Так как ∂Q по формуле (1) определяется изменением внутренней энергии dU и работой расширения∂A, то теплоемкость также зависит от изменения объема. Для твердых тел и жидкостей изменение объема при нагревании относительно невелико, поэтому для них зависимостью теплоемкости от изменения объема обычно пренебрегают. Для газов, объем которых сильно меняется с температурой, пренебрегать зависи-
3
мостью ∂Q и теплоемкости от изменения объема нельзя.
Применим уравнение (1) к различным изопроцессам идеальных газов:
а) при изохорном процессе (V = const) газ не совершает работу. По первому началу термодинамики вся теплота, сообщаемая газу в изохорном процессе, идет на изменение его внутренней энергии.
∂Q= d U= | m | CMv d T, | ∂A =0, | (4) |
| ||||
| M |
|
| |
где CMV – молярная теплоемкость газа при постоянном объеме;
б) при изобарном процессе (p = соnst) уравнение первого начала термодинамики можно записать в виде:
m | CMp d T= | m | CMv d T+ p d V, | (5) |
| ||||
| M |
| ||
где СMP – молярная теплоемкость газа при постоянном давлении. Выразим элементарную работу из уравнения Менделеева – Кла-
пейрона:
∂A= p d V= | m | R d T . | (6) |
| |||
| M |
| |
Для установления связи между молярными теплоемкостями СМP и СMV подставим (6) в (5). Получаем:
СM P−CM V= R .
Это соотношение называется уравнением Майера. Для удельных теплоемкостей Сmp и Cmv оно имеет вид:
Cmp−Cmv= MR .
Физический смысл уравнения Майера заключается в том, что при изобарном нагревании газа к нему должна быть подведена большая теплота, чем для изохорного нагревания в одном и том же диапазоне температур;
в) при изотермическом процессе (T = const) внутренняя энергия идеального газа не изменяется и вся теплота, сообщаемая газу, расходуется на совершение газом работы против внешних сил (V2 > V1 – расширение).
∂Q = ∂A , или | Q | = A | = | m | RT ln | V2 | , d U= 0, | (7) |
|
| |||||||
| 12 | 12 |
| M |
| V1 |
|
|
|
|
|
|
|
|
|
так как dT = 0, следовательно, теплоемкость равна бесконечности;
4
г) для адиабатного процесса∂Q = 0 и С = Cm = CM = 0.
Теория теплоемкостей газов, которую называют классической, в отличие от квантовой, была разработана Больцманом и Максвеллом.
Эта теория основывается на законе о равномерном распределении энер-
гии по степеням свободы молекул. Молекула одноатомного газа имеет три степени свободы поступательного движения относительно трех координатных осей. На каждую степень свободы приходится энергия:
Ei = 12 k T.
В общем случае для моля многоатомного идеального газа:
EM = NA Ei = 2i NA k T= 2i R T,
отсюда мольная теплоемкость для идеального газа:
CMV= | i | R , | СMP= CMV+ R = ( | i | +1) R. |
|
| ||||
2 |
| 2 |
| ||
Определение теплоемкости тел обычно производится в калориметрах, т.е. в сосудах, обеспечивающих теплоизоляцию исследуемого тела от внешней среды. При этом регистрируется теплота ∆Q, получаемая телом, и изменение температуры тела∆T. Теплоемкость тела находится как частное от деления∆Q на∆Т:
С = ∆∆QT.
Надежность измерения определяется в основном, качеством калориметра. Необходимо, чтобы количество теплоты, затрачиваемое на нагревание исследуемого тела, было существенно больше теплоты, расходуемой на нагревание калориметра и на потери, связанные с утечкой теплоты из установки. При измерении теплоемкости воздуха эти требования выполнить очень трудно, так как масса воздуха, заключенного в калориметре, и, следовательно, количество теплоты, идущей на его нагревание, очень малы.
Чтобы увеличить количество воздуха при неизменных размерах установки, в данной работе воздух продувается сквозь калориметр, внутри которого установлен нагреватель. Определяются количество теплоты ∂Q, отдаваемое нагревателем, масса m протекающего воздуха и изменение его температуры∆Т. Удельная теплоемкость воздуха при постоянном давлении находится по определению:
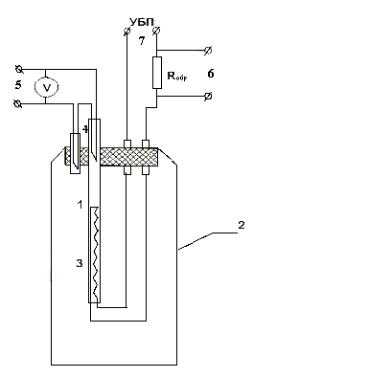
| 5 |
| |
Сmp= |
| ∆Q | (8) |
| m ∆T | ||
|
|
| |
5.УСТРОЙСТВО, ПРИНЦИП РАБОТЫ УСТАНОВКИ И МЕТОДИКА ИЗМЕРЕНИЙ
Принципиальная схема установки показана на рис.1. Воздух прокачивается компрессором через трубку 1, размещенную в теплоизолирующей оболочке 2.
Измерение расхода воздуха производится по перепаду давлений на капилляре, который вместе с трубой образует единую проточную магистраль. Протекая через трубку, воздух нагревается электрической спиралью 3. Разность температур на входе и выходе трубки измеряется дифференциальной термопарой 4. ЭДС термопары измеряется вольтметром, подключаемым к ней через разъем 5. Электрический нагреватель
3 питается постоянным током от | Рис. 1. Схема установки |
блока питания УБП, подключенно- |
го к нагревателю через соответствующие разъемы. Напряжение на нагревателе измеряется вольтметром, подключаемым через разъемы 7. Ток в нагревателе определяется по измеренному вольтметром, подключаемым к разъемам 6, напряжению UR на образцовом сопротивлении
Rобр = 0,1 Ом:
Iн= | UR |
| (9) | |
Rобр. | ||||
|
| |||
Определяем количество теплоты, отдаваемое нагревателем возду- | ||||
ху за время t, по закону Джоуля-Ленца: |
| |||
∆Q = Iн Uн t | (10) | |||
Массовый расход воздуха z через трубку, определяемый как масса воздуха, протекающего через поперечное сечение трубки в единицу времени
|
|
|
| 6 |
|
|
|
|
|
|
|
|
| z = | m |
|
|
| (11) | ||
находим по формуле Пуазейля: | t |
|
| |||||||
|
|
|
|
|
| |||||
π r4 |
|
|
|
|
|
| ||||
|
|
| ρ ∆P t |
|
|
| ||||
|
| η = |
| 0 |
|
|
| , |
| |
| m |
| 8 l V |
| ||||||
|
|
|
|
|
| |||||
где объем V = | , откуда |
|
|
|
|
|
|
|
| |
ρ |
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| |
|
|
|
| π r4 ρ ∆p |
| |||||
|
| z = |
| 0 |
|
|
| (12) | ||
|
|
| 8 l η |
|
| |||||
|
|
|
|
|
|
|
| |||
где радиус капилляра – r0 = 4,5 10−4 м, длина капилляра -l = 6 10−2 м , коэффициент внутреннего трения воздуха при данной температуре –
η = 1,810-5 мкгс, перепад давлений на концах капилляра -∆р =ρжgh, где
плотность воды ρж =103 кг/м3, перепад уровней жидкости в манометре – h , плотность воздуха -ρ = 1,29 кг/м3.
Перепад температур на концах трубки определяем по измеренной термо ЭДС ε из формулы
где коэффициент α = 0,00671 В/град для данной термопары. Подставляя (9), (10), (11), (12), (13) в уравнение (8), получаем ра-
бочую формулу
Cmp= B | Uн U |
| |
R | , | (14) | |
| |||
| h ε |
| |
где B – постоянная для данной установки:
B = | 8 l α η | = 0,356 | Дж м | . |
π g Rобр ρж ρ r04 |
| |||
|
| кг К В | ||
7
6.ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
6.1.Присоединить гибкий шланг к воздушным штуцерам на обоих модулях (см. рис. 2).
6.2.Соединить проводами клеммы источника питания на измерительном модуле и клеммы «Ист. пит.» на модуле стенда.
6.3.Соединить проводами клеммы «Вольтм.» модуля стенда и
клеммы « » и «U» мультиметра измерительного стенда.
6.4.Вывести регулятор напряжения источника питания на измерительном стенде в крайнее положение, вращая ручку против часовой стрелки. На переключателе пределов мультиметра (левый вертикальный ряд кнопок) установить предел напряжения 20В, для этого нажать кнопку «20В». Все остальные кнопки переключателя пределов должны быть отжаты.
6.5.На измерительном стенде включить тумблеры «Сеть», «Источник питания», «Компрессор», а также движок выключателя мультиметра (он находится справа вверху на панели мультиметра).
6.6.Нажмите клапан «Напуск» на модуле стенда и добейтесь, чтобы разность уровней жидкости h в U-образномманометре составила
50-100мм.
6.7.Нажать кнопку RА на модуле стенда и с индикатора мультиметра произвести отсчёт напряжения UН на нагревателе, при этом величина этого напряжения устанавливается поворотом ручки регулятора напряжения источника питания по часовой стрелке.
6.8.Нажать кнопку RБ на модуле стенда и с индикатора мультиметра произвести отсчёт напряжения UR на образцовом сопротивлении, для этого переключить предел измерения мультиметра на 200 мВ (нажать кнопку «200mV» на переключателе пределов мультиметра).
6.9.Нажать кнопку на модуле стенда и снять отсчет напряжения на термопаре по индикатору мультиметра в момент, когда показания мультиметра перестанут изменяться (примерно через 5 минут при постоянной разности уровней h), после чего перейти на предел измерения
«20 V».
6.10.Пункты 6.7 – 6.9 повторить для следующих четырёх значений напряжения UН на нагревателе (6 В, 8 В, 10 В, 12 В). Результаты
измерений занести в таблицу. Рассчитать Cmp по формуле (14).
Рис.2. Блок-схемаустановки.
Слева показан измерительный модуль, справа – модуль стенда
9
6.11. Рассчитать удельную теплоемкость для воздуха по формуле
i |
| R |
| ||
Cmp= |
| + 2 |
| , взять i = 5, M = 0,029 кг/моль. Сравнить полученное | |
2 | M | ||||
|
|
| |||
значение со средней удельной теплоемкостью при постоянном давлении, определенное по данным лабораторной работы.
Измеряемые параметры и рассчитанная удельная теплоемкость при постоянном давлении
№ | Uн | h | ε | UR |
| Cmp | |
опыта | B | м | В | В |
| Дж |
|
| кг К | ||||||
|
|
|
|
|
| ||
1 | 2 |
|
|
|
|
|
|
2 | 4 |
|
|
|
|
|
|
3 | 6 |
|
|
|
|
|
|
4 | 8 |
|
|
|
|
|
|
5 | 10 |
|
|
|
|
|
|
7. ИССЛЕДОВАТЕЛЬСКОЕ ЗАДАНИЕ
Оценить величину тепловых потерь, считая, что потери тепла зависят только от распределения температур вдоль стенок, а значит, перепада температур на спаях термопары, и не зависят от мощности нагревателя и потока воздуха. Это позволяет экспериментальным путем найти и исключить потери тепла в калориметре. Тогда:
Сmp= | ∆Q | = | IHVH− N | , | |
m ∆T | m ∆T | ||||
|
|
|
где IHVH – мощность, выделяемая нагревателем; N – мощность тепловых потерь; m – масса воздуха, проходящего через калориметр за единицу времени;∆Q – теплота;∆Т – разность температур.
1. По полученным результатам для всех измерений постройте графики, откладывая по оси абсцисс мощность нагревателя IHVH , а по оси ординат – величину m∆T; угол наклона прямой, проведенной через точки графика, определяет искомую теплоемкость воздуха при посто-
studfiles.net
Теплоемкость воздуха при постоянном давлении
Пример 1.14. Вычислить среднюю теплоемкость воздуха при постоянном давлении в пределах 200—800 °С, считая зависимость теплоемкости от температуры нелинейной. [c.44]Ср— удельная теплоемкость воздуха при постоянном давлении (в кал/г) [c.317] Ср — теплоемкость воздуха при постоянном давлении (0,23 ккалЫг X [c.496]
Приводятся значения удельной теплоемкости воздуха при постоянном давлении Ср, кДж/(кг К). [c.719]
ПРИЛОЖЕНИЕ 1 Плотность и теплоемкость воздуха при постоянном давлении [c.239]
Пример 2. Пользуясь табличными данными, подсчитать а) истинную молекулярную теплоемкость воздуха при постоянном давлении [c.125]
Стандартная теплоемкость воздуха при постоянном давлении иТ = 21,1°С по данным Шу и Сейджа [4]. [c.77]
В сороковых годах XIX в. станет ясно, что открытие этоги закона могло произойти в любое время после 1823 г. Уравнение состояния газа было установлено. Гей-Люссак провел свой опыт. Деларош и Берар измерили теплоемкость воздуха при постоянном давлении. Пуассон вывел уравнение для отношения ср/с ,. Дезорм и Клеман провели свой опыт. Лаплас правильно объяснил опыт Дезорма и Клемана. Вычисление (dPIdv) по уравнению Пуассона стало возможным. Вся подготовительная работа для открытия закона была выполнена. Нехватало только одного—понимг -пия смысла полученных результатов. [c.73]
Э—теплоемкость воздуха при постоянном давлении, ккал/(м °С) [c.82]
Для последующих вычислений необходимо знать энтальпию влажного воздуха. Если удельное влагосодержание ие превышает предела насыщения, антальпия влажного воздуха слагается из энтальпии сухого воздуха и энтальпии водяного пара. О-бозиачим удельную теплоемкость воздуха при постоянном давлении через с-ра, тогда энтальпия сухого воздуха будет равна 1а = Сра(. Энтальпию водяного пара V при низкой температуре можно выразить следующим образом [c.539]
Пример 1. Компрессор засасывает 800 м /час воздуха и сжимает его в 3 ступенях от 1 до 40 ата. Температура поступающего в компрессор воздуха 22° С отношение теплоемкости воздуха при постоянном давлении к теплоемкости при постоянном давлении v. = 1,40. Подсчитать а) объем и температуру воздуха после 3-й ступени, если бы он после 1-й и 2-й ступеней не охлаждался б) как распределится повышение температуры после каждой ступени, если 1-я ступень сжимает его до 3 ата, 2-я—до 10 ата, 3-я — до 40 ата (при этом после каждой ступени воздух проходит холодильники, охлаждаясь в них до своей первоначальной температуры (22° С), т. е. температура поступающего в каждую ступень воздуха одна и та же) [c.171]
Ср г = 0,24 ккал/(кг-°С) —удельная теплоемкость воздуха при постоянном давлении [c.97]
Здесь о — массовый расход воздуха, кг/с с — средняя теплоемкость воздуха (при постоянном давлении), Дж/(кг-К). [c.135]
Ср — весовая теплоемкость воздуха при постоянном давлении, ккал кг-град [c.10]
Пример 2. Энтальпия жидкого воздуха, кипящего при абсолютном давлении 1 кгс/слА, условно принята равной 22,5 ккал/кг. Из табл. 2.1 видно, что температура кипения воздуха при 1 кгс/см в конце испарения равна —191,8 °С, а теплота парообразования (испарения) составляет 49,07 ккал/кг. Примем теплоемкость воздуха при постоянном давлении Ср 0,24 ккал/(кг-град). Тогда энтальпия воздуха, например, при +20 °С составит [c.43]
Температурная зависимость истинной мольной теплоемкости воздуха выражается упрощенным уравнением = (6,50 + 0,001 Т) 4,19. Вычислить а) истинную мольную и удельную теплоемкости воздуха при постоянном давлении и постоянном объеме при 400°С, [c.62]
Вычислить а) истинную мольную и удельную теплоемкости воздуха при постоянных давлении й объеме при 400° С, если соотношение ср/с для воздуха равно 1,4 [c.49]
В сороковых годах XIX в. станет ясно, что открытие первого начала могло произойти в любое время после 1823 г. Уравн
www.chem21.info
Экспериментальное определение теплоёмкости воздуха при постоянном давлении методом протока
1. Цель работы:экспериментальное определение теплоёмкости воздуха при постоянном давлении методом протока. Изучение метода измерения разности температур.
2. Теоретические основы работы.
Теплоёмкостью называется отношение количества теплоты, полученного телом (веществом) при бесконечно малом изменении его состояния, к вызванному этим изменением приращению температуры. Удельная теплоёмкость – теплоёмкость единицы массы вещества. Таким образом:
Здесь δQ – элементарное количество теплоты, полученное телом, dT — элементарное изменение температуры тела, m – масса тела. Теплоёмкость одного моля вещества равна:
(2.2)
где μ – молярная масса вещества.
Теплоёмкость идеального газа зависит от вида процесса, в результате которого к телу подводится теплота. Для расчёта теплоёмкости одного моля идеального газа следует воспользоваться первым началом термодинамики для элементарного квазистатического процесса. Квазистатический термодинамический процесс – процесс, происходящий настолько медленно, что термодинамическая система в течение всего процесса остаётся близкой к состоянию равновесия.
δQ = dU + pdV (2.3)
здесь dU – элементарное изменение внутренней энергии газа,
р – давление газа,
dV – элементарное изменение объёма.
Для вычисления молярной теплоёмкости необходимо знать термическое и калориметрическое уравнение состояния идеального газа. Для одного моля газа уравнение Клайперона имеет вид:
pV = RT (2.4)
Выражение для внутренней энергии:
где R – универсальная газовая постоянная,
i – число степеней свободы молекулы газа.
Из (2.1) – (2.5) получим соотношение для молярных теплоёмкостей идеального газа в изохорном и изобарном процессах:
Cμ,v= ( )v= R (2.6)
Для воздуха эффективная молярная масса μэфф= 0,029 кг/моль, число степеней свободы молекулы (азот и кислород – двухатомные газы) i=5. Отсюда теоретическое значение удельной теплоёмкости воздуха при постоянном давлении равно:
Ср = 7R/2mэфф = 1003 Дж/кг*К (2.8)
Воздух считается идеальным газом.
3. Описание установки. Вывод расчётных формул.
Экспериментальная установка состоит из функционального модуля № 7 и приборного модуля № 1, содержащего источник питания ИП , мультиметр mV и компрессор, прокачивающий воздух через пневмопровод функционального модуля (рис. 3.1).
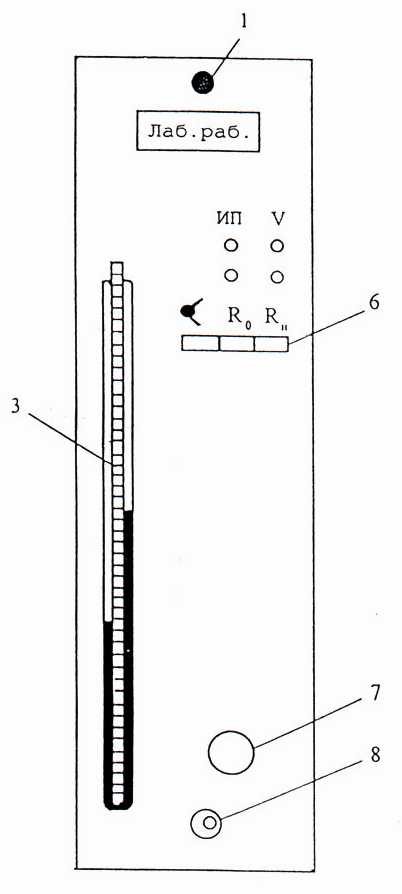
На передней панели функционального модуля №7 расположены крепёжный винт 1, табличка с названием работы 2, водяной манометр с измерительной линейкой 3, гнёзда 4, 5 для подключения источника питания и мультиметра (вольтметра) mV, трехгрупповой переключатель 6 для последовательного подключения мультиметра (вольтметра) к термопаре, балластному сопротивлению и нагревателю, клапан 7 и штуцер 8 пневмопривода для подачи воздуха. Схема экспериментальной установки показана на рис 3.2.
Воздух прокачивается компрессором через трубку
9, размещённую в теплоизолирующей оболочке (сосуде Дьюара) 10. Измерение
массового расхода воздуха производится по
перепаду давления на капилляре 11, который вместе с трубкой 9, образует единую
проточную магистраль. Протекая через трубку 9, воздух нагревается электрической
спиралью 12. Разность температур воздуха, на входе и на выходе сосуда Дьюара
измеряется дифференциальной термопарой 13. Электрический нагреватель 12
питается постоянным током от блока питания приборного модуля №1, подключенного
к клеммам 4 модуля №7. Для определения значения электрического тока в
нагревателе последовательно с ним включено балластное сопротивление R0 ТермоЭДС термопары,
напряжение на балластном сопротивлении напряжение на нагревателе измеряются
мультиметром, подключенным с помощью соединительных проводов к клеммам 5
кнопочного переключателя 6. Массовый расход воздуха в сосуде Дьюара измеряется
с помощью водяного U-манометра по перепаду давления на капилляре. В работе
определяется количество тепла, отдаваемое нагревателем воздуха в единицу
времени ΔQ = Iн*Uн, массовый расход воздуха m, разность температур воздуха, ΔQ на входе и
выходе сосуда Дьюара. Удельная теплоёмкость воздуха определяется из соотношения
Ср = Q/qm = Iн*Uн/qm (2.9)
где:
– ток в нагревателе, рассчитывается по измеренному мультиметром напряжению на образцовом сопротивлении, А;
U0 – напряжение на балластном сопротивлении, В,
R0 – номинальное значение балластного сопротивления, Ом;
m – массовый расход воздуха, кг/с.
4.Порядок выполнения работы.
1. Соединить источник питания приборного модуля с помощью проводов с гнёздами 4 нагревателя модуля № 7.
2. Соединить мультиметр (вольтметр) приборного модуля с помощью проводов с гнёздами 5 кнопочного переключателя объектов измерений модуля №7.
3. Соединить штуцер 8 пневмопровода модуля №7 со штуцером компрессора приборного модуля с помощью резинового шланга.
4. Включить электропитание приборного модуля, компрессора, источник питания, мультиметр (вольтметр).
5. Убедиться в том, что на выходе источника питания отсутствует напряжение. При этом регулятор напряжения необходимо повернуть против часовой стрелки до упора.
6. Установить предел измерения напряжения мультиметра (вольтметра) 20 В.
7. Нажать кнопку Rн кнопочного переключателя модуля №7 для измерения напряжения на нагревателе Uн.
vunivere.ru
§ 5.6. Теплоемкости газа при постоянном объеме и постоянном давлении
При введении понятия теплоемкости мы не обращали внимание на одно существенное обстоятельство: теплоемкости зависят не только от свойств вещества, но и от процесса, при котором осуществляется теплопередача.
Если нагревать тело при постоянном давлении, то оно будет расширяться и совершать работу. Для нагревания тела на 1 К при постоянном давлении ему нужно передать большее количество теплоты, чем при таком же нагревании при постоянном объеме.
Жидкие и твердые тела расширяются при нагревании незначительно, и их теплоемкости при постоянном объеме и постоянном давлении мало различаются. Но для газов это различие существенно. С помощью первого закона термодинамики можно найти связь между теплоемкостями газа при постоянном объеме и постоянном давлении.
Теплоемкость газа при постоянном объеме Найдем молярную теплоемкость газа при постоянном объеме. Согласно определению теплоемкости
где ΔT — изменение температуры. Если процесс происходит при постоянном объеме, то эту теплоемкость обозначим через Cv. Тогда
(5.6.1)
При постоянном объеме работа не совершается. Поэтому первый закон термодинамики запишется так:
(5.6.2)
Изменение
энергии одного моля достаточно
разреженного (идеального) одноатомного
газа равно: 
(см.
§ 4.8).
Следовательно, молярная теплоемкость при постоянном объеме одноатомного газа равна:
(5.6.3)
Теплоемкость газа при постоянном давлении
Согласно определению теплоемкости при постоянном давлении Ср
(5.6.4)
Работа, которую совершит 1 моль идеального газа, расширяющегося при постоянном давлении, равна:
(5.6.5)
* Из формулы (5.6.5) видно, что универсальная газовая постоянная численно равна работе, которую совершает 1 моль идеального газа при постоянном давлении, если температура его увеличивается на 1К.
Это следует из выражения для работы газа при постоянном давлении А’ = pΔV и уравнения состояния (для одного моля) идеального газа pV = RT.
Внутренняя энергия идеального газа от объема не зависит. Поэтому и при постоянном давлении изменение внутренней энергии ΔU = CVΔT, как и при постоянном объеме. Применяя первый закон термодинамики, получим:
(5.6.6)
Следовательно, молярные теплоемкости идеального газа связаны соотношением
(5.6.7)
Впервые эта формула была получена Р. Майером и носит его имя.
В случае идеального одноатомного газа
(5.6.8)
Теплоемкость идеального газа при изотермическом процессе
Можно формально ввести понятие теплоемкости и при изотермическом процессе. Так как при этом процессе внутренняя энергия идеального газа не меняется, какое бы количество теплоты ему ни было передано, то теплоемкость бесконечна.
Молярная теплоемкость идеального газа при постоянном давлении больше теплоемкости при постоянном объеме на величину универсальной газовой постоянной R.
§ 5.7. Адиабатный процесс
Мы рассмотрели изотермический, изобарный и изохорный процессы. После ознакомления с первым законом термодинамики появляется возможность изучить еще один процесс, — это процесс, протекающий в системе при отсутствии теплообмена с окружающими телами. (Но работу над окружающими телами система может совершать.)
Процесс в теплоизолированной системе называют адиабатным.
При адиабатном процессе Q = 0 и согласно закону (5.5.3) изменение внутренней энергии происходит только за счет совершения работы:
(5.7.1)
Конечно, нельзя окружить систему оболочкой, абсолютно исключающей теплообмен. Но в ряде случаев реальные процессы очень близки к адиабатным. Существуют оболочки, обладающие малой теплопроводностью, например двойные стенки с вакуумом между ними. Так изготовляются термосы.
Процесс можно считать адиабатным даже без теплоизолирующей оболочки, если он происходит достаточно быстро, т. е. так, чтобы за время процесса не происходило заметного теплообмена между системой и окружающими телами.
Согласно выражению (5.7.1) при совершении над системой положительной работы, например при сжатии газа, внутренняя энергия его увеличивается; газ нагревается. Наоборот, при расширении газ сам совершает положительную работу (А’ > 0), но А < 0 и внутренняя энергия его уменьшается; газ охлаждается.
Зависимость давления газа от его объема при адиабатном процессе изображается кривой, называемой адиабатой (рис. 5.9). Адиабата обязательно идет круче изотермы. Ведь при адиабатном процессе давление газа уменьшается не только за счет увеличения объема, как при изотермическом процессе, но и за счет уменьшения его температуры.
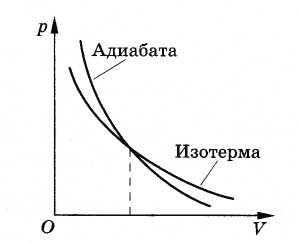
Рис. 5.9
Адиабатные процессы широко используются в технике. Они играют немалую роль в природе.
Нагревание воздуха при быстром сжатии нашло применение в двигателях Дизеля. В этих двигателях отсутствуют системы приготовления и зажигания горючей смеси, необходимые для обычных бензиновых двигателей внутреннего сгорания. В цилиндр засасывается не горючая смесь, а атмосферный воздух. К концу такта сжатия в цилиндр с помощью специальной форсунки впрыскивается жидкое топливо (рис. 5.10). К этому моменту температура сжатого воздуха так велика, что горючее воспламеняется.
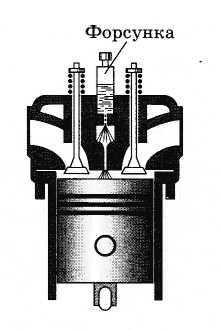
Рис. 5.10
Так как в двигателе Дизеля сжимается не горючая смесь, а воздух, то степень сжатия у этого двигателя больше, а значит, коэффициент полезного действия (КПД) двигателей Дизеля выше, чем у обычных двигателей внутреннего сгорания. Кроме того, они могут работать на более дешевом низкосортном топливе. Есть, однако, у двигателя Дизеля и недостатки: необходимость высоких степеней сжатия и большое рабочее давление делают эти двигатели массивными и вследствие этого более инерционными — они медленнее набирают мощность. Двигатели Дизеля более сложны в изготовлении и эксплуатации, тем не менее они постепенно вытесняют обычные бензиновые двигатели, используемые в автомобилях.
Охлаждение газа при адиабатном расширении происходит в грандиозных масштабах в атмосфере Земли. Нагретый воздух поднимается вверх и расширяется, так как атмосферное давление падает с высотой. Это расширение сопровождается значительным охлаждением. В результате водяные пары конденсируются и образуются облака.
studfiles.net
Лабораторная работа № 11 Определение удельной теплоемкости воздуха при постоянном давлении.
СОДЕРЖАНИЕ
Лабораторная работа № 11 Определение удельной теплоемкости воздуха при постоянном давлении. | 4 |
Лабораторная работа № 12 Определение отношения теплоемкостей воздуха Сp/Сv методом Клемана – Дезорма. | 11 |
Лабораторная работа № 13 Определение удельной теплоты кристаллизации и измерения энтропии при охлаждении олова. | 18 |
Лабораторная работа № 14 Измерение коэффициента теплопроводности воздуха методом нагретой нити. | 24 |
Лабораторная работа № 15 Измерение коэффициента внутреннего трения воздуха и длинны свободного пробега молекул воздуха. | 31 |
Лабораторная работа №16 Определение коэффициента внутреннего трения по методу Стокса. | 36 |
Лабораторная работа № 17 Определение теплового значения и тепловых потерь калориметрического сосуда. | 41 |
Лабораторная работа № 18 Проверка абсолютной шкалы температур Кельвина газовым термометром постоянного объёма. | 48 |
Лабораторная работа № 19 Изучение эффекта Джоуля-Томсона. | 51 |
Лабораторная работа № 20 Изучение распределения электронов по энергиям. | 57 |
Приложение | 63 |
Описание установки: На передней панели модуля расположены крепежный винт 1 , табличка с названием работы 2 , водяной U-манометр с измерительной линейкой 3, гнезда 4 и 5 для подключения источника питания и мультиметра (вольтметра), трехгрупповой переключатель 6 для последовательного подключения мультиметра (вольтметра) к термопаре, балластному сопротивлению и нагревателю, клапан 7 для подачи воздуха в установку. На модуле, входящем в модификацию 1 дополнительно расположен штуцер 8 пневмопровода.
Воздух прокачивается компрессором через трубку 9 (Рис.2), размещенную в теплоизолирующей оболочке (сосуде Дьюара) 13. Измерение массового расхода воздуха производится по перепаду давления на капилляре 12, который вместе с трубкой 9 образует единую проточную магистраль. Протекая через трубку 9 , воздух нагревается электрической спиралью 10. Разность температур воздуха на входе и выходе сосуда Дьюара измеряется дифференциальной термопарой 11. Электрический нагреватель 10 питается постоянным током от блока питания приборного модуля №10, подключенного к клеммам 4 модуля №1 (Рис. 1) . Для определения значения электрического тока в нагревателе последовательно с ним включено балластное сопротивление R0. Термо-э.д.с. термопары, напряжение на балластном сопротивлении и напряжение на нагревателе измеряется мультиметром (вольтметром) приборного модуля, подключенным с помощью соединительных проводов к клеммам 5 кнопочного переключателя 6 . Массовый расход воздуха в сосуде Дьюара измеряется с помощью водяного U-манометра по перепаду давления на капилляре.
В работе определяется количество тепла, отдаваемое нагревателем воздуха в единицу времени Q = IHUH, массовый расход воздуха m, разность температур воздуха Т на входе и выходе сосуда Дьюара. Теплоемкость воздуха определяется из соотношения
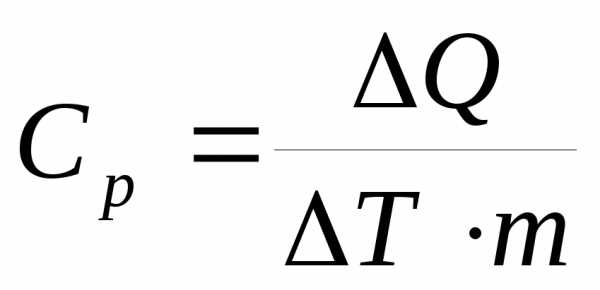(1)
где:
–
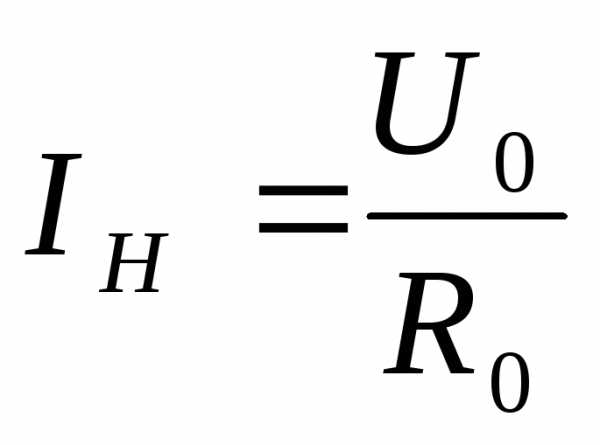ток в нагревателе, А;
U0 – напряжение на балластном сопротивлении, В;
R0 – номинальное значение балластного сопротивления, Ом;
m – массовый расход воздуха, кг ∙ с-1.
Порядок выполнения работы.
1.Соединить источник питания приборного модуля с помощью проводов с гнездами 4 нагревателя модуля № 1.
2. Соединить мультиметр (вольтметр) приборного модуля с помощью проводов с гнездами 5 кнопочного переключателя объектов измерений модуля № 1.
3. В модификации 1 соединить штуцер 8 пневмопровода модуля № 1 со штуцером компрессора приборного модуля с помощью резинового шланга.
4. Включить электропитание приборного модуля, компрессор источник питания, мультиметр (вольтметр). Установить предел измерения напряжений мультиметра (вольтметра) 20 В.
5. Убедиться в том, что на выходе источника питание отсутствует напряжение. При этом регулятор напряжения необходимо повернуть против часовой стрелки до упора.
6. Нажать кнопку RH кнопочного переключателя модуля N 1 для измерения напряжения на нагревателе.
7. Регулятором напряжения источника питания установить первое из заданных значений напряжения на нагревателе: UH1=2В, UH2=4В, UH3=6В. UH4= 8 В, UH5=10В.
Произвести отсчет и записать измеренное значение в таблицу 5.
8. Нажать кнопку 7 клапана пневмопровода для подачи воздуха в сосуд Дьюара и удерживать ее до окончания операций, указанных в пунктах 9, 10.
9. Нажать кнопку “<” переключателя модуля № 1, переключить предел измерения мультиметра (вольтметра) на 200 mВ.
10. Наблюдать за показаниями мультиметра (вольтметра), измеряющего термо-э.д.с. термопары, до тех пор пока прибор не будет регистрировать постоянное во времени значение термо-э.д.с. (примерно через 3 – 5 минут после открытия клапана пневмопровода). Произвести отсчет и записать измеренное значение в таблицу 5.
11. Нажать кнопку R6 кнопочного переключателя модуля № 1 и произвести отсчет напряжения на балластном сопротивлении. Результат записать в таблицу 5.
12. Произвести отсчет разности уровней жидкости в U-манометре и определить перепад давлений на концах капилляра по формуле:
P=gh (2)
где:
- плотность жидкости, 1000 кг ∙ м-3,
h – перепад уровней, м.
13. Определить расход воздуха в установке, используя соотношение Пуазейля
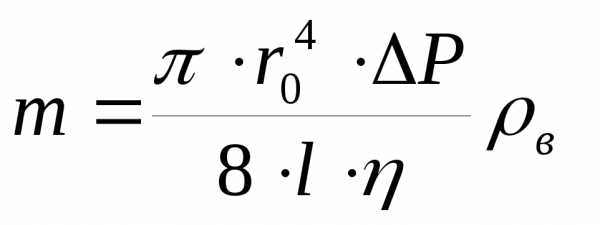(3)
где:
r0 – радиус капилляра, м;
l – длина капилляра, м;
– коэффициент внутреннего трения воздуха при данной температуре. Па
ρв – плотность воздуха,1.2 кг/м3.
14. Пункты 6…12. повторить для следующих четырех значений напряжения на нагревателе (п. 7).
Данные установки и таблица результатов измерений.
Радиус капилляра r0 = 0.5 мм;
Длина капилляра l = 37 мм;
Балластное сопротивление R0= 0.1 Ом
Коэффициент внутреннего трения воздуха ( 20оС) = 1.812*10-5 кг*м-1с-1
Таблица 5
№ п/п | Un, B | UR, mB | h, м | ∆ | Q, Дж/с | ∆T, K |
1. | ||||||
2. | ||||||
… |
ε,
mBОбработка результатов измерений.
1) Определить по ртутному термометру температуру воздуха в лаборатории и принять ее равной температуре воздуха на входе в калориметра Твх.
2) По табл.6 определить термо-э.д.с. Е хромель-копелевой термопары, соответствующую Твх.
3) Прибавляя к каждому измеренному значению Е, значение Евх определить по таблице б температуру воздуха на выходе из калориметр Твых.
4) Рассчитать разность температур воздуха на выходе и входе калориметра = Твых – Твх.
5) По полученным данным построить график линейной зависимости IHUH = f(). График должен иметь вид, изображенный на рис.5.
6) Провести оптимальную прямую через набор экспериментальных точек. Ограничить полосу, в которой находятся экспериментальные точки прямыми, параллельными оптимальной линии и проходящими через наиболее удаленные от оптимальной прямой точки (на рис.3 это пунктирные линии)
7) Определить тангенс угла наклона оптимальной прямой по формуле
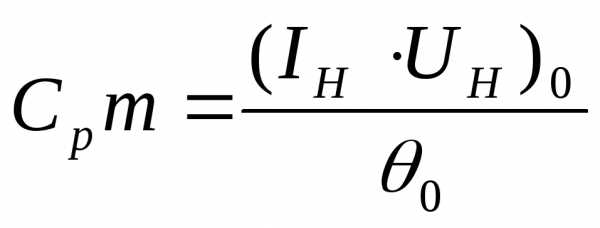(4)
Значения (IHUH) и 0 берут близкими к значениям для последнего опыта (см. рис. 5).
8) Рассчитать удельную теплоемкость воздуха при постоянном давлении:
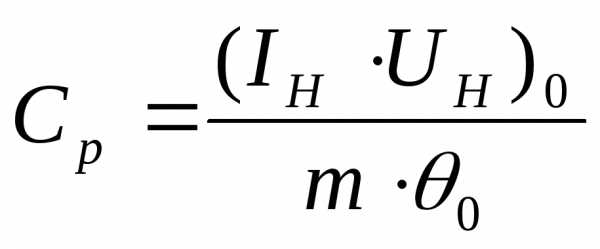(5)
Погрешность Ср рассчитать по формуле:
(6)
Абсолютные погрешности для разности температур 0 и мощности (IHUH) определяются из графика (рис.3).
Градуировочная характеристика хромель-копелевой термопары (по СТ СЭВ 1059-78)
Таблица 1.
t,0C | Термодвижущая сила, mB | |||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
0 | 0.00 | 0.06 | 0.12 | 0.19 | 0.25 | 0.32 | 0.38 | 0.45 | 0.51 | 0.58 |
10 | 0.64 | 0.71 | 0.77 | 0.84 | 0.90 | 0.97 | 1.03 | 1.10 | 1.17 | 1.23 |
20 | 1.30 | 1.37 | 1.43 | 1.50 | 1.57 | 1.63 | 1.70 | 1.77 | 1.84 | 1.90 |
30 | 1.97 | 2.04 | 2.11 | 2.18 | 2.24 | 2.31 | 2.38 | 2.45 | 2.52 | 2.58 |
40 | 2.65 | 2.72 | 2.79 | 2.86 | 2.93 | 3.00 | 3.07 | 3.14 | 3.21 | 3.28 |
50 | 3.35 | 3.35 | 3.42 | 3.49 | 3.56 | 3.63 | 3.70 | 3.84 | 3.91 | 3.98 |
60 | 4.05 | 4.12 | 4.19 | 4.26 | 4.33 | 4.40 | 4.47 | 4.54 | 4.61 | 4.68 |
70 | 4.76 | 4.83 | 4.90 | 4.97 | 5.04 | 5.11 | 5.18 | 5.25 | 5.32 | 5.39 |
80 | 5.46 | 5.54 | 5.61 | 5.68 | 5.75 | 5.82 | 5.89 | 5.96 | 6.03 | 6.10 |
90 | 6.17 | 6.25 | 6.32 | 6.39 | 6.46 | 6.53 | 6.61 | 6.68 | 6.75 | 6.82 |
100 | 6.89 | 6.97 | 7.04 | 7.11 | 7.18 | 7.25 | 7.33 | 7.40 | 7.48 | 7.55 |
110 | 7.62 | 7.70 | 7.77 | 7.84 | 7.92 | 7.99 | 8/07 | 8.14 | 8.21 | 8.29 |
120 | 8.36 | 8.44 | 8.51 | 8.59 | 8.66 | 8.74 | 8.81 | 8.89 | 8.98 | 9.04 |
130 | 9.11 | 9.19 | 9.26 | 9.34 | 9.41 | 9.49 | 9.56 | 9.64 | 9.71 | 9.79 |
140 | 9.86 | 9.94 | 10.01 | 10.09 | 10.16 | 10.24 | 10.32 | 10.39 | 10.47 | 10.56 |
150 | 10.62 | 10.70 | 10.77 | 10.85 | 10.93 | 11.00 | 11.08 | 11.16 | 11.23 | 11.31 |
160 | 11.39 | 11.47 | 11.54 | 11.62 | 11.70 | 11.78 | 11.86 | 11.93 | 12.01 | 12.09 |
170 | 12.17 | 12.25 | 12.32 | 12.40 | 12.48 | 12.56 | 12.64 | 12.72 | 12.80 | 12.88 |
180 | 12.96 | 13.04 | 13.12 | 13.20 | 13.28 | 13.36 | 13.44 | 13.52 | 13.60 | 13.68 |
190 | 13.76 | 13.84 | 13.92 | 14.00 | 14.08 | 14.16 | 14.24 | 14.32 | 14.40 | 14.48 |
200 | 14.57 | 14.65 | 14.73 | 14.81 | 14.89 | 14.97 | 15.05 | 15.13 | 15.21 | 15.29 |
210 | 15.38 | 15.46 | 15.51 | 15.62 | 15.70 | 15.79 | 15.87 | 15.95 | 16.03 | 16.11 |
220 | 16.20 | 16.28 | 16.36 | 16.44 | 16.53 | 16.61 | 16.69 | 16.78 | 16.86 | 16.94 |
230 | 17.03 | 17.11 | 17.19 | 17.27 | 17.36 | 17.44 | 17.52 | 17.61 | 17.69 | 17.77 |
№1 №10
Рис.1.
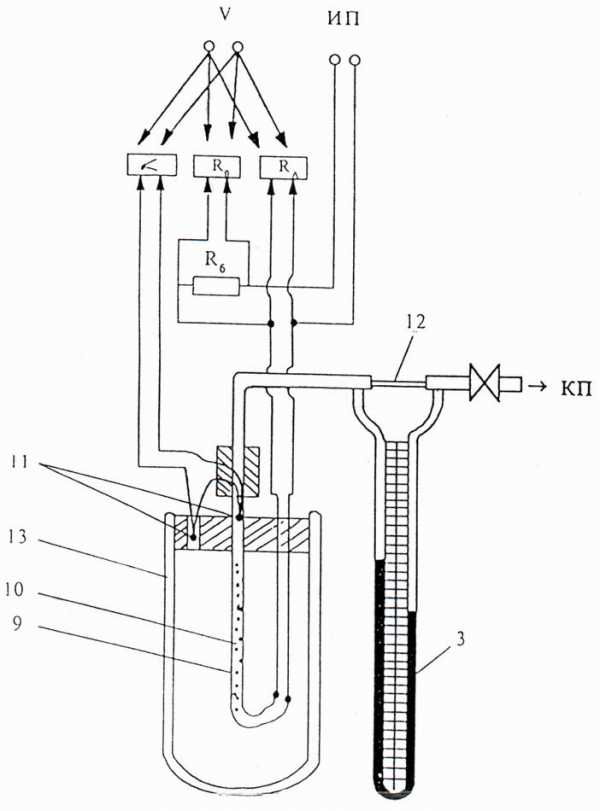
Рис.2.
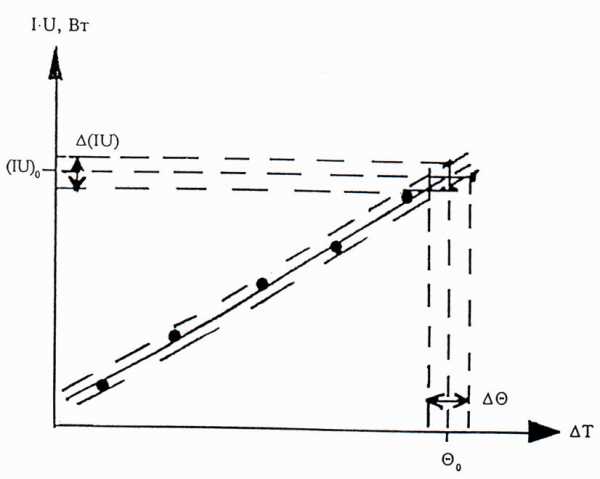
Рис.3.
Контрольные вопросы.
Дайте определение теплоёмкости.
Запишите формулу Пуазеля. Получить массовый расход воздуха.
Получить формулу для определения удельной теплоёмкости воздуха.
Связь Ср и Сv.
Объясните суть метода определения удельной теплоёмкости воздуха.
Лабораторная работа № 12
Определение отношения теплоемкостей воздуха Cp/Cv методом Клемана-Дезорма.
Описание установки:
На передней панели модуля расположены крепежный винт 1 , табличка с названием работы 2 , водяной U-манометр с измерительной линейкой 3 , вентиль напуска воздуха 4, вентиль сброса давления 5 На модуле, входящем в модификацию 1, дополнительно расположен штуцер пневмопровода 6.
Модуль содержит металлический баллон 7 (Рис.4), внутренняя поверхность которого покрыта теплоизолирующей мастикой и наполнена воздухом. Баллон соединен с водяным U-манометром З и компрессором с помощью резиновых пневмопроводов. Быстрое изменение давления в баллоне происходит практически без теплообмена с окружающей средой. Поэтому процесс, происходящий при открывании клапана 5, с достаточной точностью можно считать адиабатным. С помощью компрессора в баллон накачивают воздух, затем закрывают кран баллона 4. Через несколько минут температура воздуха в баллоне станет равной температуре в лаборатории. Обозначим эту температуру It (Рис.7). Давление воздуха в баллоне р при этом равно
Pt= Р0 + Р’, (2)
где: рв– атмосферное давление,
р’- избыточное давление воздуха, которое можно определить по показаниям манометра. Выбирается мысленно в баллоне объем V вдали от клапана. Считается, что число молекул в этом объеме неизменно. Начальное состояние воздуха в объеме характеризуется параметрами p1, T1, V1 . Если открыть на короткое время клапан, часть воздуха выйдет из баллона, давление станет равным р2=р0, выбранный объем увеличится до значения V2. Температура воздуха понизится, так как при вытекании из баллона воздух совершает работу против атмосферного давления (Т2 <T1). В момент времени, когда клапан закрывают, состояние выбранного объема характеризуется параметрами р2 , Т2., V2. Считая переход из состояния 1 в состояние 2 адиабатным процессом, получим:
P1V1γ = p2V2γ (3)
После того как клапан закрыли, происходит изохорный процесс теплообмена с окружающей средой; температура воздуха приближается к температуре в лаборатории T1, давление воздуха по окончании этого процесса равно:
Р3 = р0 + р“ (4)
где: р” измеряется по манометру. Параметры воздуха после окончания изохорного процесса р3, Т1, V3. Причем V3=V2. Так как температура воздуха в первом и третьем состоянии одинаковы, а число молекул в выбранном нами объеме постоянно (объем V выбран вдали от клапана), то для состояний 1 и 3 по закону Бойля – Мариотта
P1∙V1 = p3∙V3 = p2∙V2 (5)
Решая систему уравнении (3) и (5), получается:
(P3/P1)
=P2/P1 (6)
Прологарифмировав это соотношение, находятся
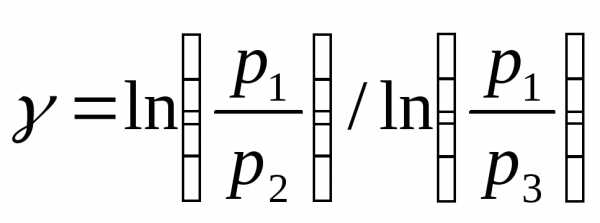
(7)
Используя соотношения (2) и (4), получается
(8)
Так как избыточные давления р’ и р’’ весьма малы по сравнению с атмосферным давлением р0, используется разложение функции типа ln(1+x) в ряд, ограничиваясь первым членом разложения (при « 1). При этом ln(1+х)≈ х. Отсюда из (8) получается:
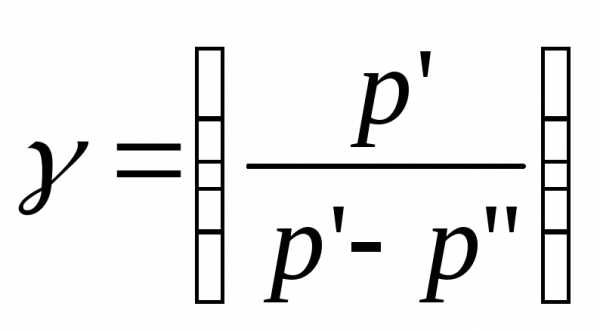(9)
Избыточное давление, определяемое по манометру, можно выразить соотношением:
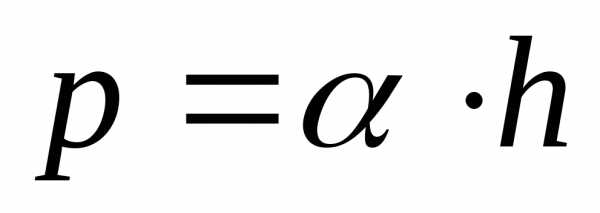
, (10)
где:
h – разность уровней жидкости в манометре,
α- постоянный для данного манометра коэффициент, зависящий от плотности жидкости. Из (9) и (10) получается:
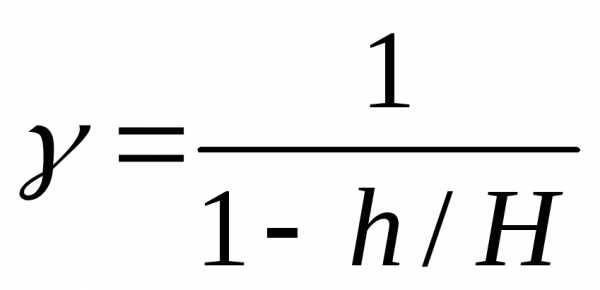, (11)
где:
H и h – разности уровней жидкости в манометре в первом и третьем состояниях.
Необходимо
учесть, что значение h0 соответствует
условию, что клапан закрыли точно в
момент окончания адиабатного процесса.
Если закрыть клапан раньше (до выравнивания
давлений) или спустя некоторое время
после адиабатного процесса, то результат
вычислений по формуле (11) даст в первом
случае завышенное, а во втором случае
заниженное значение
.Для
получения наиболее точного экспериментального
значения необходимо закрыть клапан
точно в момент окончания адиабатного
процесса. Так как время протекания
адиабатного процесса неизвестно,
значение разности уровнейh0 определяется косвенным графическим
методом (Рис.
8).
Функциональный модуль №2 (рис. 4,7).
1. В модификации 2 соединить штуцер пневмопровода модуля №2 со штуцером компрессора приборного модуля с помощью резинового шланга.
2. Включить электропитание приборного модуля, компрессор.
3. Нажать клавишу 4 клапана “Напуск” и накачать в баллон воздух так, чтобы разность уровней жидкости в манометре стала равно) 250-300 мм
4. Отпустить клавишу 4 клапана “Напуск”, выждать 2-3 минут: до тех пор, пока температура воздуха в баллоне не станет равной температуре окружающей среды.
Произвести дополнительную регулировку разностей уровней (в дальнейших опытах начальную разность уровней нужно поддерживать постоянной). По нижнему уровню мениска определить уровни жидкости L1 и L2 в коленах манометра. Записать значения L1, L2, Н = L1 – L2 в таблицу 2.
5.
Резко нажать на клапан сброса 5, соединив
баллон с атмосферой. Одновременно
включить секундомер. Выдержать клапан
открытым течение заданного времени ;
после этого отпустить клапан. Через 3
минуты (после того, как уровни жидкости
в манометре стабилизируются), определить
уровни L1(
) и L2(
), записать значения L1(
), L2(
), в таблицу 2.
6.
Повторить опыты (пункты 3 … 5) не менее
пяти раз для разных значений 
:
10, 15, 20, 25, 30, 35 секунд. Следить за тем,
чтобы начальная разность уровней Н была
постоянной. Примечание: накачивать
воздух в баллон нужно медленно (чтобы
избежать значительного повышения
температуры воздуха в баллоне) и осторожно
(чтобы нижний уровень жидкости не достиг
колена манометра).
Таблица 2
№ опыта | τ , с | L1 | L2 | |
1 2 … |
7. Обработка результатов измерений.
1) Рассчитать значения ln h и ln (τ + 1) для всех значений τ.
2) Нанести полученные экспериментальные точки на график (рис. 8), где по оси абсцисс отложено время ln (τ + 1), по оси ординат – значения ln h.
Примечание. Масштаб графика согласовывать с преподавателем.
3) Аппроксимировать полученную зависимость прямой линией, экстраполировав ее до пересечения с осью ординат. Точка пересечения имеет координату In h .
4)
Определить значение h0.
5)
По формуле (11) определить экспериментальное
значение 
.
6)
Для оценки погрешности необходимо
сделать следующее: для каждой
экспериментальной точки вверх и вниз
отложить на графике значения ln(h+∆h) и ln(h-∆h).
Полученные таким образом точки образуют
полосу. Обозначим через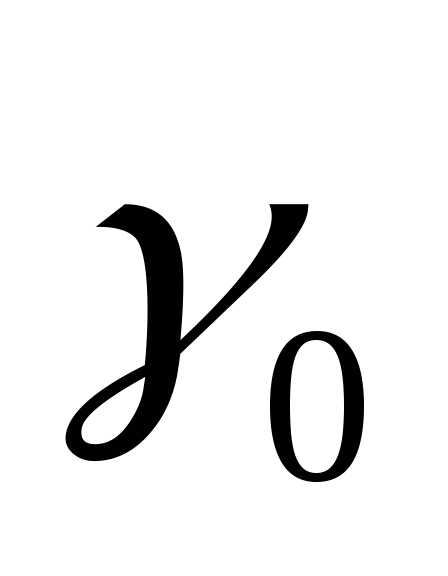 
расстояние
между точками пересечения прямых,
ограничивающих полосу с осью ординат.
Тогда:
(65)
Учитывая,
что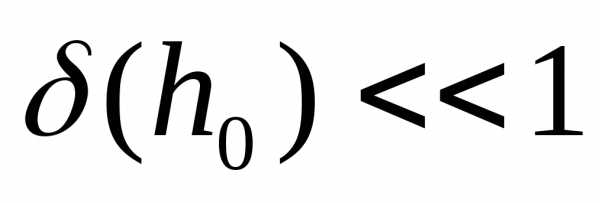 
,
разложим (70 ) в ряд Маклорена, ограничившись
первыми двумя членами разложения. Отсюда
получится
; .
Таким образом,
Окончательно получаем соотношение для погрешности косвенного измерения :
(66)
7) Записать результат с учетом погрешности измерения.
8) Сравнить экспериментальное значение Y с теоретическим значением (воздух считать двухатомным идеальным газом).
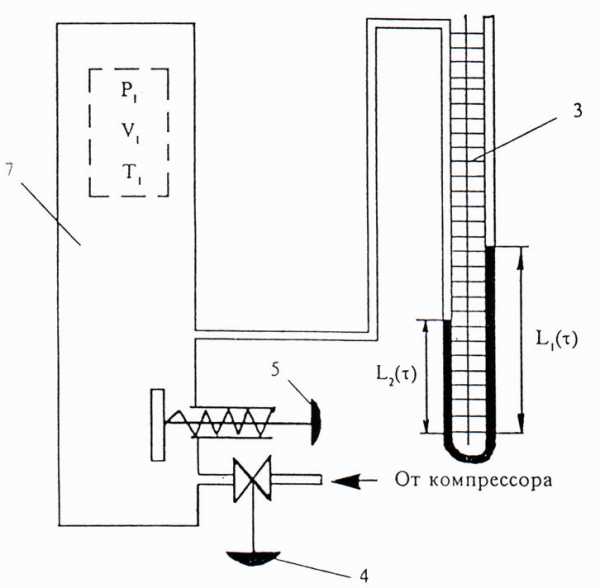
Рис.4.
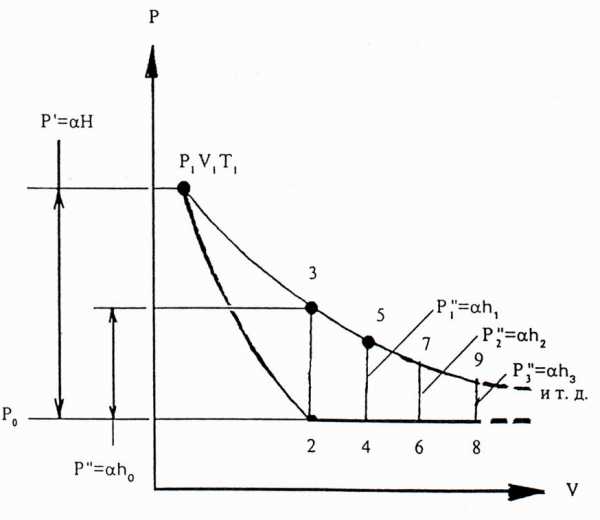
Рис.5.
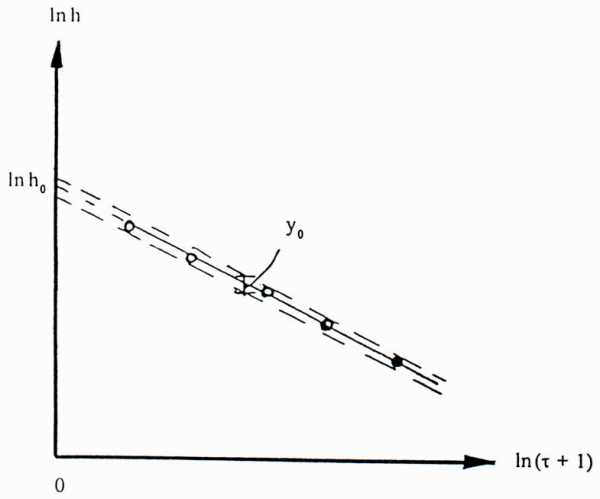
Рис.6.
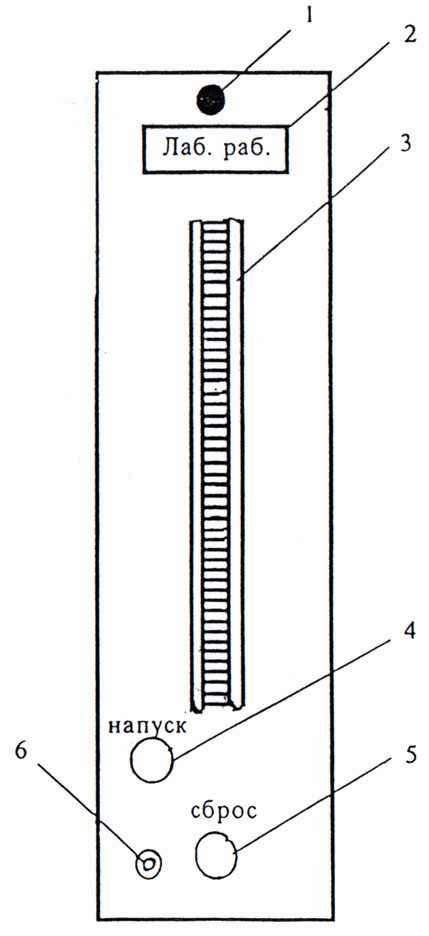
Рис.7.
studfiles.net
Определение удельной теплоёмкости воздуха при постоянном давлении
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального
образования
ФИЛИАЛ
Дальневосточного Федерального университета
(ДВПИ имени Куйбышева)
в г. Петропавловске
– Камчатском
Отчет
по
лабораторной работе
Тема:
Определение удельной
теплоёмкости воздуха
при постоянном давлении
Выполнили: Студенты группы ЭУД-10
Исаченко А. И.
Давыдова Ю. Р.
«____»__________20___г
Проверил:
Малкин Е.И.
«____»__________20___г
г. Петропавловск-Камчатский
2011 г.
Цели
и задачи лабораторной
работы: В соответствии с порядком проведения
эксперимента выполнить измерения; построить
график зависимости; экспериментально
определить удельную теплоёмкость воздуха
при постоянном давлении; на основании
результатов вычислить абсолютную и относительную
погрешности измерения.
Краткие теоретические сведения:
- Теплоёмкость – физическая величина, описывающая связь между подведённой в термодинамическую систему (соответственно отведенной из неё) теплотой и произошедшим изменением температуры.
- Теплоёмкость – отношение бесконечно малого количества теплоты, полученного телом, соответствующему приращению его температуры.
- Определение теплоёмкости тел обычно производится в калориметрах, то есть в сосудах, обеспечивающих теплоизоляцию исследуемого тела от внешней среды.
- Удельная теплоёмкость – физическая величина, определяющая, какое количество теплоты должно получить или отдать тело весом 1 кг, чтобы его температура изменилась на 1 градус Кельвина.
- Из всех существующих в природе жидкостей вода имеет наибольшую удельную теплоёмкость.
Схема
экспериментальной
установки: Калориметр представляет
собой стеклянную трубку с вакуумной теплоизолирующей
оболочкой. 1)Компрессор служит для подачи
воздуха в калориметр; 2)Измерение подачи
воздуха осуществляется с помощью ротаметра;
3)Нагреватель, закрепленный в калориметре,
сделан в виде спирали; 4)Для измерения
температуры применяются хромель-копелевые
термопары, расположенные на входе в калориметр
и на выходе нагревателя.
Порядок
выполнения эксперимента:
- Подсоединить мультиметр с помощью проводов к разъёмам на передней панели установки.
- Включить питание установки тумблером «Сеть», измеритель температуры тумблером, компрессор тумблером.
- Включить питание нагревателя кнопочным выключателем источника питания и установить первое значение напряжения Uн = 3 В.
- Включить мультиметр и измерить точное значение Uн и Uо, переключая тумблер в соответствующие положения.
- Через 4-5 минут (по достижении стационарного режима) произвести отсчёт температур Т1 и Т2 по измерителю 2ТРМО и объёмного расхода воздуха G по ротаметру.
- Пункты 3-5 повторить для следующих значений напряжения на нагревателе: Uн = 4; 5; 6; 7 В.
Расчетные
формулы.
Так как то .
Особое
значение имеют теплоёмкости при
постоянном объёме CV и постоянном
давлении CP.
Если V=const, то dV=0 и, следовательно
Если
же постоянным является давление, то отношение переходит в частную производную , в этом случае .
На основании
определения энтальпии можно переписать .
По закону
Джоуля , а из уравнения Клапейрона – Менделеева .
Учитывая
выше сказанное, получаем: , или . Это соотношение называется уравнением
Роберта Майера.
Таблица.
| № п/п | t1 | t2 | t | Uн, B | U0, мB | I, A | Q, Bт | G, м3/с | Cp |
| 1 | 24.8 | 32.7 | 7.9 | 3 | 0.02 | 0.2 | 0.6 | 7.78E-05 | 976.49 |
| 2 | 25 | 38.3 | 13.3 | 4 | 0.025 | 0.25 | 1 | 7.78E-05 | 966.70 |
| 3 | 25.2 | 44.7 | 19.5 | 5 | 0.032 | 0.32 | 1.6 | 7.78E-05 | 1054.95 |
| 4 | 25.3 | 52.1 | 26.8 | 6 | 0.039 | 0.39 | 2.34 | 7.78E-05 | 1122.60 |
| 5 | 25.5 | 63.2 | 37.7 | 7 | 0.045 | 0.45 | 3.15 | 7.78E-05 | 1074.27 |
| Ср= | 1039.00 |
Вычисление
абсолютной и относительной
погрешностей.
Абсолютная погрешность:Δ=
Относительная
погрешность: =2,86%
Вывод: Рассчитывая удельную теплоёмкость воздуха при постоянном давлении, мы получили среднее значение равное 1039.00, при этом были использованы результаты проведённого эксперимента и градуировка шкалы ротаметра. На основании результатов получили абсолютную погрешность равную 29,68302 и относительную погрешность равную 2,86%
stud24.ru
Удельная теплоемкость при постоянном давлении
Ср—удельная теплоемкость при постоянном давлении. [c.16]Ср, Си — удельные теплоемкости при постоянном давлении и при постоянном объеме, ктл/кг °С к — показатель адиабаты [c.5]
Показатель политропы сжатия или расширения т зависит от степени подогрева или охлаждения газа в процессе сжатия. Для идеального случая изменения состояния без теплообмена и без потерь показатель политропы т равен отношению значений удельной теплоемкости при постоянном давлении и при постоянном объеме, т. е. показателю адиабаты к = [c.32]
Ср — удельная теплоемкость при постоянном давлении, Дж/(кг К) [c.4]
Ср — удельная теплоемкость при постоянном давлении, Дж/(кг К) р — плотность, кг/м . [c.8]
Поскольку стационарные течения, при описании которых целесообразнее использовать с , а ие с , преобладают на практике, то иногда обозначение с применяется без индекса при этом имеется в виду удельная теплоемкость при постоянном давлении с . [c.15]
В идеальных газах разность между удельными теплоемкостями при постоянном давлении Ср и при постоянном объеме Сг,, кДж/(кмоль К), [c.155]
Сол—коэффициент сопротивления для ускоряющихся частиц Ср— удельная теплоемкость при постоянном давлении Со— удельная теплоемкость при постоянном объеме [c.14]
Пример VI. 1. Определить коэффициент теплопроводности сухого воздуха при атмосферном давлении и температуре 80° С, если его удельная теплоемкость при постоянном давлении равна Ср = 0,244 ккал [кг-град) и динамическая вязкость [1 = 0,021 спз. [c.146]Используем уравнение (VII,34) для расчета коэффициента теплоотдачи а, внутренней пленки жидкости, имеющей следующие свойства удельная теплоемкость при постоянном давлении Ср = 2500 Дж/(кг К) коэффициент [c.137]
Ср — средняя удельная теплоемкость при постоянном давлении, кДж/(кг К) [c.8]
Проверить правило Дюлонга и Пти для меди, цинка и кадмия при 17° С. Даны истинные удельные теплоемкости при постоянном давлении [c.17]
Какое количество теплоты потребуется для нагревания 1 воздуха от О до ГС при постоянном объеме и начальном давлении Р= 1,013-10 Па Плотность воздуха при нормальных условиях 1,29 кг/м , удельная теплоемкость при постоянном давлении Ср= 1,01 Дж/(г-К). [c.11]
Система (6.7.7) —(6.7.10) отличается от системы (6.1.15), (6.1.16) данной главы наличием в уравнении вихря величин, зависящих от температуры и концентрации (подъемные силы), и двух дополнительных уравнений, относящихся к типу уравнение переноса с диссипацией (см. гл. 4). Диссипативными коэффициентами здесь являются — коэффициент теплопроводности, О — коэффициент диффузии. Коэффициент Ср в (6.7.9) — удельная теплоемкость при постоянном давлении. Граничные условия, для этой системы включают граничные условия для ноля скорости, рассматривавшиеся выше в 6.1, и граничные условия для температуры и ноля концентрации. Последние могут быть трех основных типов [c.205]
В зависимости от процесса, в котором сообщается тепло, различают для газов и паров удельную теплоемкость при постоянном давлении и теплоемкость при постоянном объеме. Для жидкостей это различие, как незначительное, не проводится. [c.584]
В этих уравнениях Я —коэффициент теплопроводности при давлении р и температуре ккал[М ч- град-, Яо — коэффициент теплопроводности при давлении 1 кГ/см и температуре ккал/м-наград Укр —удельный объем в критической точке, м 1кг V — удельный объем газа при давлении р и температуре t, м /кг-, Аср — прирост удельной теплоемкости при постоянном давлении от давления в 1 кГ/см до давления р при постоянной температуре ккал/кг град. [c.174]
Истинные и средние значения удельных теплоемкостей при постоянном давлении и постоянном объеме для газовых фаз некоторых углеводородов приведены в табл. 1-8. Удельная массовая теплоемкость при конкретных температурах для жидкой фазы приведена ниже. [c.25]
П — объем выпускаемой продукции, или ирои.чводительиосгь ироиесса. ср — удельная теплоемкость при постоянном давлении, [c.11]
Идеальные газы. Удельная теплоемкость идеальных газон близка к удельной теплоемкости реальных газон н области низких (принедепн1>1х) данлений и нисокнх (приведенных) температур. Эта область примерно ограничена значениями 7 >2 для рг4 для />гУдельная теплоемкость при постоянном давлении Ср составляет 30 кДж/(кмоль-К), причем она возрастает с ростом температуры. [c.155]
Тпблццл 3. Зависимость удельной теплое
www.chem21.info