Расчет потерь давления на местные сопротивления вентиляция формулы: Расчет потерь давления на местные сопротивления вентиляция формулы

Расчет потерь давления на местные сопротивления вентиляция формулы

Главная » Блог » Расчет потерь давления на местные сопротивления вентиляция формулы

Расчет потери давления в воздуховодах в системе вентиляции

Вентиляция › Услуги по вентиляции › Проектирование вентиляции ›

Когда известны параметры воздуховодов (их длина, сечение, коэффициент трения воздуха о поверхность), можно рассчитать потери давления в системе при проектируемом расходе воздуха.

Общие потери давления (в кг/кв.м.) рассчитываются по формуле:

P = R*l + z,

где R – потери давления на трение в расчете на 1 погонный метр воздуховода, l – длина воздуховода в метрах, z – потери давления на местные сопротивления (при переменном сечении).

1. Потери на трение:

В круглом воздуховоде потери давления на трение P тр считаются так:

Pтр = (x*l/d) * (v*v*y)/2g,

где x – коэффициент сопротивления трения, l – длина воздуховода в метрах, d – диаметр воздуховода в метрах, v – скорость течения воздуха в м/с, y – плотность воздуха в кг/куб. м., g – ускорение свободного падения (9,8 м/с2).

• Замечание: Если воздуховод имеет не круглое, а прямоугольное сечение, в формулу надо подставлять эквивалентный диаметр, который для воздуховода со сторонами А и В равен: dэкв = 2АВ/(А + В)

2. Потери на местные сопротивления:

Потери давления на местные сопротивления считаются по формуле:

z = Q* (v*v*y)/2g,

где Q – сумма коэффициентов местных сопротивлений на участке воздуховода, для которого производят расчет, v – скорость течения воздуха в м/с, y – плотность воздуха в кг/куб.м., g – ускорение свободного падения (9,8 м/с2). Значения Q содержатся в табличном виде.

Метод допустимых скоростей

При расчете сети воздуховодов по методу допустимых скоростей за исходные данные принимают оптимальную скорость воздуха (см. таблицу). Затем считают нужное сечение воздуховода и потери давления в нем.

Порядок действий при аэродинамическом расчете воздуховодов по методу допустимых скоростей:

• Начертить схему воздухораспределительной системы. Для каждого участка воздуховода указать длину и количество воздуха, проходящего за 1 час.
• Расчет начинаем с самых дальних от вентилятора и самых нагруженных участков.
• Зная оптимальную скорость воздуха для данного помещения и объем воздуха, проходящего через воздуховод за 1 час, определим подходящий диаметр (или сечение) воздуховода.
• Вычисляем потери давления на трение P тр.
• По табличным данным определяем сумму местных сопротивлений Q и рассчитываем потери давления на местные сопротивления z.
• Располагаемое давление для следующих ветвлений воздухораспределительной сети определяется как сумма потерь давления на участках, расположенных до данного ветвления.

В процессе расчета нужно последовательно увязать все ветви сети, приравняв сопротивление каждой ветви к сопротивлению самой нагруженной ветви. Это делают с помощью диафрагм. Их устанавливают на слабо нагруженные участки воздуховодов, повышая сопротивление.

Таблица максимальной скорости воздуха в зависимости от требований к воздуховоду

Назначение	Основное требование
Бесшумность	Мин. потери напора
Магистральные каналы	Главные каналы	Ответвления
Приток	Вытяжка	Приток	Вытяжка
Жилые помещения	3	5	4	3	3
Гостиницы	5	7.5	6.5	6	5
Учреждения	6	8	6.5	6	5
Рестораны	7	9	7	7	6
Магазины	8	9	7	7	6

Примечание: скорость воздушного потока в таблице дана в метрах в секунду

Метод постоянной потери напора

Данный метод предполагает постоянную потерю напора на 1 погонный метр воздуховода.

На основе этого определяются размеры сети воздуховодов. Метод постоянной потери напора достаточно прост и применяется на стадии технико-экономического обоснования систем вентиляции:

• В зависимости от назначения помещения по таблице допустимых скоростей воздуха выбирают скорость на магистральном участке воздуховода.
• По определенной в п.1 скорости и на основании проектного расхода воздуха находят начальную потерю напора (на 1 м длины воздуховода). Для этого служит нижеприведенная диаграмма.
• Определяют самую нагруженную ветвь, и ее длину принимают за эквивалентную длину воздухораспределительной системы. Чаще всего это расстояние до самого дальнего диффузора.
• Умножают эквивалентную длину системы на потерю напора из п.2. К полученному значению прибавляют потерю напора на диффузорах.

Теперь по приведенной ниже диаграмме определяют диаметр начального воздуховода, идущего от вентилятора, а затем диаметры остальных участков сети по соответствующим расходам воздуха.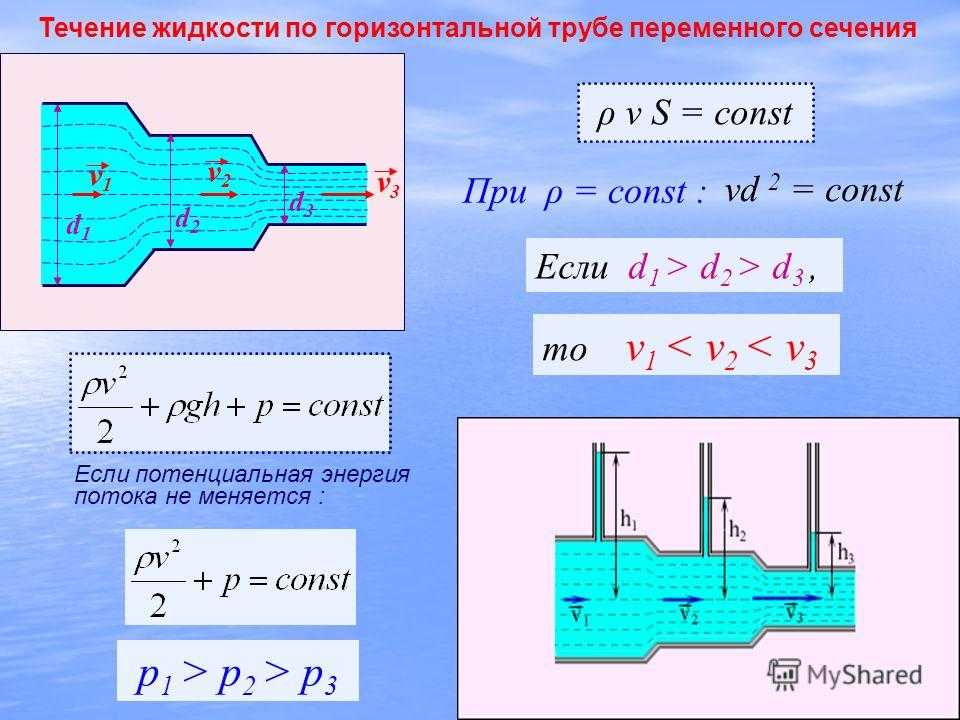

При этом принимают постоянной начальную потерю напора.

Диаграмма определения потерь напора и диаметра воздуховодов

Использование прямоугольных воздуховодов

В диаграмме потерь напора указаны диаметры круглых воздуховодов. Если вместо них используются воздуховоды прямоугольного сечения, то необходимо найти их эквивалентные диаметры с помощью приведенной ниже таблицы.

Примечания:

• Если позволяет пространство, лучше выбирать круглые или квадратные воздуховоды;
• Если места недостаточно (например, при реконструкции), выбирают прямоугольные воздуховоды. Как правило, ширина воздуховода в 2 раза больше высоты).

В таблице по горизонтальной указана высота воздуховода в мм, по вертикальной – его ширина, а в ячейках таблицы содержатся эквивалентные диаметры воздуховодов в мм.

Таблица эквивалентных диаметров воздуховодов

Размеры	150	200	250	300	350	400	450	500
250	210	245	275
300	230	265	300	330
350	245	285	325	355	380
400	260	305	345	370	410	440
450	275	320	365	400	435	465	490
500	290	340	380	425	455	490	520	545
550	300	350	400	440	475	515	545	575
600	310	365	415	460	495	535	565	600
650	320	380	430	475	515	555	590	625
700		390	445	490	535	575	610	645
750		400	455	505	550	590	630	665
800		415	470	520	565	610	650	685
850			480	535	580	625	670	710
900			495	550	600	645	685	725
950			505	560	615	660	705	745
1000			520	575	625	675	720	760
1200				620	680	730	780	830
1400					725	780	835	880
1600						830	885	940
1800						870	935	990

Получите коммерческое предложение на email:

Нужна консультация? Звоните:

8(495) 118-27-34

Информация, размещенная на сайте, носит ознакомительный характер и ни при каких условиях не является публичной офертой.

Расчет потери напора воздуха в системе вентиляции

Назначение	Основное требование
Бесшумность	Мин. потери напора
Магистральные каналы	Главные каналы	Ответвления
Приток	Вытяжка	Приток	Вытяжка
Жилые помещения	3	5	4	3	3
Гостиницы	5	7.5	6.5	6	5
Учреждения	6	8	6.5	6	5
Рестораны	7	9	7	7	6
Магазины	8	9	7	7	6

Исходя из этих значений следует рассчитывать линейные параметры воздуховодов.

Расчет нужно начинать с составления схемы системы вентиляции с обязательным указанием пространственного расположения воздуховодов, длины каждого участка, вентиляционных решеток, дополнительного оборудования для очистки воздуха, технической арматуры и вентиляторов. Потери определяются вначале по каждой отдельной линии, а потом суммируются. По отдельному технологическому участку потери определяются с помощью формулы P = L×R+Z, где P – потери воздушного давления на расчетном участке, R – потери на погонном метре участка, L – общая длина воздуховодов на участке, Z – потери в дополнительной арматуре системы вентиляции.

Для расчета потерь давления в круглом воздуховоде используется формула Pтр. = (L/d×X) × (Y×V)/2g. X – табличный коэффициент трения воздуха, зависит от материала изготовления воздуховода, L – длина расчетного участка, d – диаметр воздуховода, V – требуемая скорость воздушного потока, Y – плотность воздуха с учетом температуры, g – ускорение падения (свободного). Если система вентиляции имеет квадратные воздуховоды, то для перевода круглых значений в квадратные следует пользоваться таблицей № 2.

Табл. № 2. Эквивалентные диаметры круглых воздуховодов для квадратных

Размеры	150	200	250	300	350	400	450	500
250	210	245	275
300	230	265	300	330
350	245	285	325	355	380
400	260	305	345	370	410	440
450	275	320	365	400	435	465	490
500	290	340	380	425	455	490	520	545
550	300	350	400	440	475	515	545	575
600	310	365	415	460	495	535	565	600
650	320	380	430	475	515	555	590	625
700		390	445	490	535	575	610	645
750		400	455	505	550	590	630	665
800		415	470	520	565	610	650	685
850			480	535	580	625	670	710
900			495	550	600	645	685	725
950			505	560	615	660	705	745
1000			520	575	625	675	720	760
1200				620	680	730	780	830
1400					725	780	835	880
1600						830	885	940
1800						870	935	990

По горизонтали указана высота квадратного воздуховода, а по вертикали ширина. Эквивалентное значение круглого сечения находится на пересечении линий.

Потери давления воздуха в изгибах берутся из таблицы № 3.

Табл. № 3. Потери давления на изгибах

Для определения потерь давления в диффузорах используются данные из таблицы № 4.

Табл. № 4. Потери давления в диффузорах

В таблице № 5 дается общая диаграмма потерь на прямолинейном участке.

Табл. № 5. Диаграмма потерь давления воздуха в прямолинейных воздуховодах

Все отдельные потери на данном участке воздуховода суммируются и корректируются с таблицей № 6. Табл. № 6. Расчет понижения давления потока в системах вентиляции

Во время проектирования и расчетов существующие нормативные акты рекомендуют, чтобы разница в величине потерь давления между отдельными участками не превышала 10%. Вентилятор нужно устанавливать в участке системы вентиляции с наиболее высоким сопротивлением, самые удаленные воздуховоды должны иметь минимальное сопротивление. Если эти условия не выполняются, то необходимо изменять план размещения воздуховодов и дополнительного оборудования с учетом требований положений.

Калькулятор

Порядок расчета потерь давления в воздуховодах

Комментариев:

Рейтинг: 30

Сердцем любой вентиляционной системы с механическим побуждением воздушного потока является вентилятор, который создает этот поток в воздуховодах. Мощность вентилятора напрямую зависит от напора, который необходимо создать на выходе из него, а для того, чтобы определить величину этого давления, требуется произвести расчет сопротивления всей системы каналов.

Для расчета потерь давления нужна схема и размеры воздуховода и дополнительного оборудования.

Исходные данные для вычислений

Когда известна схема вентиляционной системы, размеры всех воздухопроводов подобраны и определено дополнительное оборудование, схему изображают во фронтальной изометрической проекции, то есть аксонометрии. Если ее выполнить в соответствии с действующими стандартами, то на чертежах (или эскизах) будет видна вся информация, необходимая для расчета.

Аэродинамическая характеристика по вентилятора.

1. С помощью поэтажных планировок можно определить длины горизонтальных участков воздухопроводов. Если же на аксонометрической схеме проставлены отметки высот, на которых проходят каналы, то протяженность горизонтальных участков тоже станет известна. В противном случае потребуются разрезы здания с проложенными трассами воздухопроводов. И в крайнем случае, когда информации недостаточно, эти длины придется определять с помощью замеров по месту прокладки.
2. На схеме должно быть изображено с помощью условных обозначений все дополнительное оборудование, установленное в каналах. Это могут быть диафрагмы, заслонки с электроприводом, противопожарные клапаны, а также устройства для раздачи или вытяжки воздуха (решетки, панели, зонты, диффузоры). Каждая единица этого оборудования создает сопротивление на пути воздушного потока, которое необходимо учитывать при расчете.
3. В соответствии с нормативами на схеме возле условных изображений воздуховодов должны быть проставлены расходы воздуха и размеры каналов. Это определяющие параметры для вычислений.
4. Все фасонные и разветвляющие элементы тоже должны быть отражены на схеме.

Если такой схемы на бумаге или в электронном виде не существует, то придется ее начертить хотя бы в черновом варианте, при вычислениях без нее не обойтись.

Вернуться к оглавлению

Диаграмма потери напора на каждый метр воздуховода.

Очень часто приходится сталкиваться с достаточно простыми схемами вентиляции, в которых присутствует воздухопровод одного диаметра и нет никакого дополнительного оборудования. Такие схемы просчитываются достаточно просто, но что делать, если схема сложная с множеством ответвлений? Согласно методике просчета потерь давления в воздуховодах, которая изложена во многих справочных изданиях, нужно определить самую длинную ветвь системы либо ветку с наибольшим сопротивлением. Выяснить таковую по сопротивлению на глаз удается редко, поэтому принято вести расчет по самой протяженной ветви. После этого пользуясь величинами расходов воздуха, проставленных на схеме, всю ветку делят на участки по этому признаку. Как правило, расходы меняются после разветвлений (тройников) и при делении лучше всего ориентироваться на них. Бывают и другие варианты, например, приточные или вытяжные решетки, встроенные прямо в магистральный воздуховод. Если на схеме это не показано, а такая решетка имеется, потребуется расход после нее высчитать. Участки нумеруют начиная от самого удаленного от вентилятора.

Вернуться к оглавлению

Таблица максимальной скорости воздуха.

Общая формула расчета потерь давления в воздуховодах для всей вентиляционной системы выглядит следующим образом:

HB = ∑(Rl + Z), где:

• HB — потери давления во всей системе воздуховодов, кгс/м²;
• R — сопротивление трению 1 м воздухопровода эквивалентного сечения, кгс/м²;
• l — протяженность участка, м;
• Z — величина давления, теряемого воздушным потоком в местных сопротивлениях (фасонных элементах и дополнительном оборудовании).

Примечание: значение площади поперечного сечения воздуховода, участвующее в расчете, принимается изначально как для круглой формы канала. Сопротивление трению для каналов прямоугольной формы определяется по площади сечения, эквивалентному круглому.

Расчет начинают от самого отдаленного участка №1, затем переходят ко второму участку и так далее. Результаты вычислений по каждому участку складываются, о чем и говорит математический знак суммирования в расчетной формуле. Параметр R зависит от диаметра канала (d) и динамического давления в нем (Рд), а последнее, в свою очередь, зависит от скорости движения воздушного потока. Коэффициент абсолютной шероховатости стенок (λ) традиционно принимается как для воздухопровода из оцинкованной стали и составляет 0,1 мм:

R = (λ / d) Рд.

Диаграмма определения потерь напора и диаметра воздуховодов.

Пользоваться этой формулой в процессе расчета потерь давления не имеет смысла, так как значения R для различных скоростей воздуха и диаметров уже просчитаны и являются справочными величинами (Р. В. Щекин, И.Г. Староверов — справочники). Поэтому просто необходимо найти эти значения в соответствии с конкретными условиями перемещения воздушных масс и подставить их в формулу. Еще один показатель, динамическое давление Рд, который связан с параметром R и участвует в дальнейшем подсчете местных сопротивлений, тоже величина справочная. Учитывая эту связь между двумя параметрами, в справочных таблицах они приводятся совместно.

Значение Z потерь давления в местных сопротивлениях рассчитывают по формуле:

Z = ∑ξ Рд.

Знак суммирования обозначает, что нужно сложить результаты расчета по каждому из местных сопротивлений на заданном участке. Кроме уже известных параметров, в формуле присутствует коэффициент ξ. Его величина безразмерна и зависит от вида местного сопротивления. Значения параметра для многих элементов вентиляционных систем посчитаны либо определены опытным путем, поэтому находятся в справочной литературе. Коэффициенты местного сопротивления вентиляционного оборудования зачастую указывают сами производители, определив их значения опытным путем на производстве или в лаборатории.

Таблица эквивалентных диаметров воздуховодов.

Вычислив длину участка №1, количество и вид местных сопротивлений, следует правильно определить все параметры и подставить их в расчетные формулы. Получив результат, переходить ко второму участку и далее, до самого вентилятора. При этом не следует забывать о том участке воздухопровода, который расположен уже за вентиляционной установкой, ведь напора вентилятора должно хватить и на преодоление его сопротивления.

Закончив расчеты по самой протяженной ветви, производят такие же по соседней ветке, потом по следующей и так до самого конца. Обычно эти все ветви имеют много общих участков, поэтому вычисления пойдут быстрее. Целью определения потерь давления на всех ветвях есть их общая увязка, ведь вентилятор должен распределить свой расход равномерно по всей системе. То есть в идеале потери давления в одной ветви должны отличаться от другой не более чем на 10%. Простыми словами, это значит, что самое ближнее к вентилятору ответвление должно иметь самое высокое сопротивление, а дальнее — самое низкое. Если это не так, рекомендуется вернуться к пересчету диаметров воздуховодов и скоростей движения воздуха в них.

Когда по какой-либо причине увязать ветви невозможно, в них устанавливают дополнительные искусственные сопротивления — диафрагмы, которые следует подбирать. Для упрощения процесса вместо диафрагм устанавливают дроссель — клапаны, с их помощью можно сопротивление ветви регулировать, перекрывая поток заслонкой.

Как показывает практика, правильно просчитанная и отрегулированная после монтажа вентиляционная система работает безупречно.

Расчет сопротивления воздуховода калькулятор. Расчет давления в воздуховодах

Когда известны параметры воздуховодов (их длина, сечение, коэффициент трения воздуха о поверхность), можно рассчитать потери давления в системе при проектируемом расходе воздуха.

Общие потери давления (в кг/кв.м.) рассчитываются по формуле:

где R – потери давления на трение в расчете на 1 погонный метр воздуховода, l – длина воздуховода в метрах, z – потери давления на местные сопротивления (при переменном сечении).

1. Потери на трение:

В круглом воздуховоде потери давления на трение P тр считаются так:

Pтр = (x*l/d) * (v*v*y)/2g,

где x – коэффициент сопротивления трения, l – длина воздуховода в метрах, d – диаметр воздуховода в метрах, v – скорость течения воздуха в м/с, y – плотность воздуха в кг/куб.м., g – ускорение свободного падения (9,8 м/с2).

Замечание: Если воздуховод имеет не круглое, а прямоугольное сечение, в формулу надо подставлять эквивалентный диаметр, который для воздуховода со сторонами А и В равен: dэкв = 2АВ/(А + В)

2. Потери на местные сопротивления:

Потери давления на местные сопротивления считаются по формуле:

z = Q* (v*v*y)/2g,

где Q – сумма коэффициентов местных сопротивлений на участке воздуховода, для которого производят расчет, v – скорость течения воздуха в м/с, y – плотность воздуха в кг/куб.м., g – ускорение свободного падения (9,8 м/с2). Значения Q содержатся в табличном виде.

Метод допустимых скоростей

При расчете сети воздуховодов по методу допустимых скоростей за исходные данные принимают оптимальную скорость воздуха (см. таблицу). Затем считают нужное сечение воздуховода и потери давления в нем.

Порядок действий при аэродинамическом расчете воздуховодов по методу допустимых скоростей:

Начертить схему воздухораспределительной системы. Для каждого участка воздуховода указать длину и количество воздуха, проходящего за 1 час.

Расчет начинаем с самых дальних от вентилятора и самых нагруженных участков.

Зная оптимальную скорость воздуха для данного помещения и объем воздуха, проходящего через воздуховод за 1 час, определим подходящий диаметр (или сечение) воздуховода.

Вычисляем потери давления на трение P тр.

По табличным данным определяем сумму местных сопротивлений Q и рассчитываем потери давления на местные сопротивления z.

Располагаемое давление для следующих ветвлений воздухораспределительной сети определяется как сумма потерь давления на участках, расположенных до данного ветвления.

В процессе расчета нужно последовательно увязать все ветви сети, приравняв сопротивление каждой ветви к сопротивлению самой нагруженной ветви. Это делают с помощью диафрагм. Их устанавливают на слабо нагруженные участки воздуховодов, повышая сопротивление.

Таблица максимальной скорости воздуха в зависимости от требований к воздуховоду

Метод постоянной потери напора

Данный метод предполагает постоянную потерю напора на 1 погонный метр воздуховода. На основе этого определяются размеры сети воздуховодов. Метод постоянной потери напора достаточно прост и применяется на стадии технико-экономического обоснования систем вентиляции:

В зависимости от назначения помещения по таблице допустимых скоростей воздуха выбирают скорость на магистральном участке воздуховода.

По определенной в п.1 скорости и на основании проектного расхода воздуха находят начальную потерю напора (на 1 м длины воздуховода). Для этого служит нижеприведенная диаграмма.

Определяют самую нагруженную ветвь, и ее длину принимают за эквивалентную длину воздухораспределительной системы. Чаще всего это расстояние до самого дальнего диффузора.

Умножают эквивалентную длину системы на потерю напора из п.2. К полученному значению прибавляют потерю напора на диффузорах.

Теперь по приведенной ниже диаграмме определяют диаметр начального воздуховода, идущего от вентилятора, а затем диаметры остальных участков сети по соответствующим расходам воздуха. При этом принимают постоянной начальную потерю напора.

Диаграмма определения потерь напора и диаметра воздуховодов

В диаграмме потерь напора указаны диаметры круглых воздуховодов. Если вместо них используются воздуховоды прямоугольного сечения, то необходимо найти их эквивалентные диаметры с помощью приведенной ниже таблицы.

Примечания:

Если позволяет пространство, лучше выбирать круглые или квадратные воздуховоды;

Если места недостаточно (например, при реконструкции), выбирают прямоугольные воздуховоды. Как правило, ширина воздуховода в 2 раза больше высоты).

В таблице по горизонтальной указана высота воздуховода в мм, по вертикальной – его ширина, а в ячейках таблицы содержатся эквивалентные диаметры воздуховодов в мм.

Этим материалом редакция журнала „Мир Климата“ продолжает публикацию глав из книги „Системы вентиляции и кондиционирования. Рекомендации по проектированию для произ- водственных и общественных зданий“. Автор Краснов Ю.С.

Аэродинамический расчет воздуховодов начинают с вычерчивания аксонометрической схемы (М 1: 100), проставления номеров участков, их нагрузок L (м 3 /ч) и длин I (м). Определяют направление аэродинамического расчета — от наиболее удаленного и нагруженного участка до вентилятора. При сомнениях при определении направления рассчитывают все возможные варианты.

Расчет начинают с удаленного участка: определяют диаметр D (м) круглого или площадь F (м 2) поперечного сечения прямоугольного воздуховода:

Скорость растет по мере приближения к вентилятору.

По приложению Н из принимают ближайшие стандартные значения: D CT или (а х b) ст (м).

Гидравлический радиус прямоугольных воздуховодов (м):

где — сумма коэффициентов местных сопротивлений на участке воздуховодов.

Местные сопротивления на границе двух участков (тройники, крестовины) относят к участку с меньшим расходом.

Коэффициенты местных сопротивлений даны в приложениях.

Схема приточной системы вентиляции, обслуживающей 3-этажное административное здание

Пример расчета

Исходные данные:

№ участков	подача L, м 3 /ч	длина L, м	υ рек, м/с	сечение а × b, м	υ ф, м/с	D l ,м	Re	λ	Kmc	потери на участке Δр, па
решетка рр на выходе	0,2 × 0,4	3,1	—	—	—	1,8	10,4
1	720	4,2	4	0,2 × 0,25	4,0	0,222	56900	0,0205	0,48	8,4
2	1030	3,0	5	0,25× 0,25	4,6	0,25	73700	0,0195	0,4	8,1
3	2130	2,7	6	0,4 × 0,25	5,92	0,308	116900	0,0180	0,48	13,4
4	3480	14,8	7	0,4 × 0,4	6,04	0,40	154900	0,0172	1,44	45,5
5	6830	1,2	8	0,5 × 0,5	7,6	0,50	234000	0,0159	0,2	8,3
6	10420	6,4	10	0,6 × 0,5	9,65	0,545	337000	0,0151	0,64	45,7
6а	10420	0,8	ю.	Ø0,64	8,99	0,64	369000	0,0149	0	0,9
7	10420	3,2	5	0,53 × 1,06	5,15	0,707	234000	0,0312 ×n	2,5	44,2
Суммарные потери: 185
Таблица 1. Аэродинамический расчет

Воздуховоды изготовлены из оцинкованной тонколистовой стали, толщина и размер которой соответствуют прил. Н из . Материал воздухозаборной шахты — кирпич. В качестве воздухораспределителей применены решетки регулируемые типа РР с возможными сечениями: 100 х 200; 200 х 200; 400 х 200 и 600 х 200 мм, коэффициентом затенения 0,8 и максимальной скоростью воздуха на выходе до 3 м/с.

Сопротивление приемного утепленного клапана с полностью открытыми лопастями 10 Па. Гидравлическое сопротивление калориферной установки 100 Па (по отдельному расчету). Сопротивление фильтра G-4 250 Па. Гидравлическое сопротивление глушителя 36 Па (по акустическому расчету). Исходя из архитектурных требований проектируют воздуховоды прямоугольного сечения.

Сечения кирпичных каналов принимают по табл. 22.7 .

Коэффициенты местных сопротивлений

Участок 1. Решетка РР на выходе сечением 200×400 мм (рассчитывают отдельно):

№ участков	Вид местного сопротивления	Эскиз	Угол α, град.	Отношение	Обоснование	КМС
F 0 /F 1	L 0 /L ст	f прох /f ств
1	Диффузор		20	0,62	—	—	Табл. 25.1	0,09
	Отвод		90	—	—	—	Табл. 25.11	0,19
	Тройник-проход		—	—	0,3	0,8	Прил.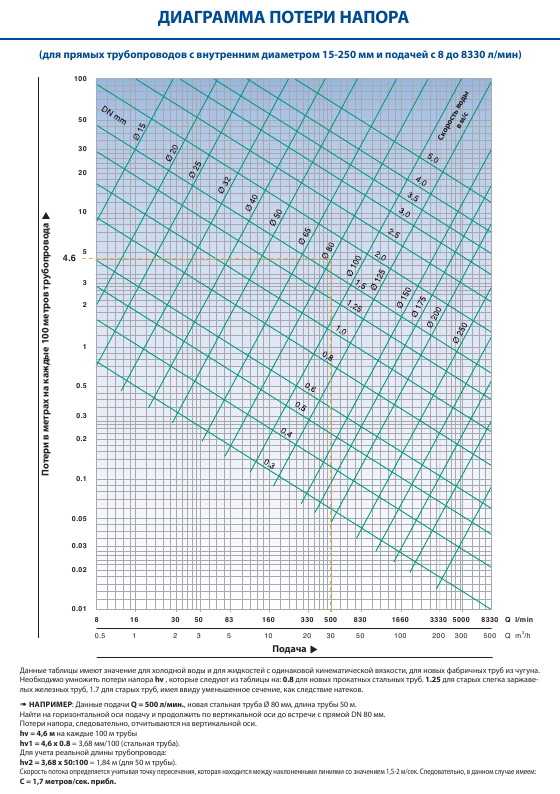 25.8	0,2
	∑ =	0,48
2	Тройник-проход		—	—	0,48	0,63	Прил. 25.8	0,4
3	Тройник-ответвление		—	0,63	0,61	—	Прил. 25.9	0,48
4	2 отвода	250 × 400	90	—	—	—	Прил. 25.11
	Отвод	400 × 250	90	—	—	—	Прил. 25.11	0,22
	Тройник-проход		—	—	0,49	0,64	Табл. 25.8	0,4
	∑ =	1,44
5	Тройник-проход		—	—	0,34	0,83	Прил. 25.8	0,2
6	Диффузор после вентилятора		h=0,6	1,53	—	—	Прил. 25.13	0,14
	Отвод	600 × 500	90	—	—	—	Прил. 25.11	0,5
	∑=	0,64
6а	Конфузор перед вентилятором			D г =0,42 м			Табл. 25.12	0
7	Колено		90	—	—	—	Табл. 25.1	1,2
	Решетка жалюзийная						Табл. 25.1	1,3
	∑ =	1,44
Таблица 2. Определение местных сопротивлений

Краснов Ю.С.,

Когда известны параметры воздуховодов (их длина, сечение, коэффициент трения воздуха о поверхность), можно рассчитать потери давления в системе при проектируемом расходе воздуха.

Общие потери давления (в кг/кв.м.) рассчитываются по формуле:

P = R*l + z,

где R – потери давления на трение в расчете на 1 погонный метр воздуховода, l – длина воздуховода в метрах, z – потери давления на местные сопротивления (при переменном сечении).

1. Потери на трение:

В круглом воздуховоде потери давления на трение P тр считаются так:

Pтр = (x*l/d) * (v*v*y)/2g,

где x – коэффициент сопротивления трения, l – длина воздуховода в метрах, d – диаметр воздуховода в метрах, v – скорость течения воздуха в м/с, y – плотность воздуха в кг/куб.м., g – ускорение свободного падения (9,8 м/с2).

• Замечание: Если воздуховод имеет не круглое, а прямоугольное сечение, в формулу надо подставлять эквивалентный диаметр, который для воздуховода со сторонами А и В равен: dэкв = 2АВ/(А + В)

2. Потери на местные сопротивления:

Потери давления на местные сопротивления считаются по формуле:

z = Q* (v*v*y)/2g,

где Q – сумма коэффициентов местных сопротивлений на участке воздуховода, для которого производят расчет, v – скорость течения воздуха в м/с, y – плотность воздуха в кг/куб. м., g – ускорение свободного падения (9,8 м/с2). Значения Q содержатся в табличном виде.

Метод допустимых скоростей

При расчете сети воздуховодов по методу допустимых скоростей за исходные данные принимают оптимальную скорость воздуха (см. таблицу). Затем считают нужное сечение воздуховода и потери давления в нем.

Порядок действий при аэродинамическом расчете воздуховодов по методу допустимых скоростей:

• Начертить схему воздухораспределительной системы. Для каждого участка воздуховода указать длину и количество воздуха, проходящего за 1 час.
• Расчет начинаем с самых дальних от вентилятора и самых нагруженных участков.
• Зная оптимальную скорость воздуха для данного помещения и объем воздуха, проходящего через воздуховод за 1 час, определим подходящий диаметр (или сечение) воздуховода.
• Вычисляем потери давления на трение P тр.
• По табличным данным определяем сумму местных сопротивлений Q и рассчитываем потери давления на местные сопротивления z.
• Располагаемое давление для следующих ветвлений воздухораспределительной сети определяется как сумма потерь давления на участках, расположенных до данного ветвления.

В процессе расчета нужно последовательно увязать все ветви сети, приравняв сопротивление каждой ветви к сопротивлению самой нагруженной ветви. Это делают с помощью диафрагм. Их устанавливают на слабо нагруженные участки воздуховодов, повышая сопротивление.

Таблица максимальной скорости воздуха в зависимости от требований к воздуховоду

Назначение	Основное требование
Бесшумность	Мин. потери напора
Магистральные каналы	Главные каналы	Ответвления
Приток	Вытяжка	Приток	Вытяжка
Жилые помещения
Гостиницы
Учреждения
Рестораны
Магазины

Примечание: скорость воздушного потока в таблице дана в метрах в секунду

Метод постоянной потери напора

Данный метод предполагает постоянную потерю напора на 1 погонный метр воздуховода. На основе этого определяются размеры сети воздуховодов. Метод постоянной потери напора достаточно прост и применяется на стадии технико-экономического обоснования систем вентиляции:

• В зависимости от назначения помещения по таблице допустимых скоростей воздуха выбирают скорость на магистральном участке воздуховода.
• По определенной в п.1 скорости и на основании проектного расхода воздуха находят начальную потерю напора (на 1 м длины воздуховода). Для этого служит нижеприведенная диаграмма.
• Определяют самую нагруженную ветвь, и ее длину принимают за эквивалентную длину воздухораспределительной системы. Чаще всего это расстояние до самого дальнего диффузора.
• Умножают эквивалентную длину системы на потерю напора из п.2. К полученному значению прибавляют потерю напора на диффузорах.

Теперь по приведенной ниже диаграмме определяют диаметр начального воздуховода, идущего от вентилятора, а затем диаметры остальных участков сети по соответствующим расходам воздуха. При этом принимают постоянной начальную потерю напора.

Диаграмма определения потерь напора и диаметра воздуховодов

Использование прямоугольных воздуховодов

В диаграмме потерь напора указаны диаметры круглых воздуховодов. Если вместо них используются воздуховоды прямоугольного сечения, то необходимо найти их эквивалентные диаметры с помощью приведенной ниже таблицы.

Примечания:

• Если позволяет пространство, лучше выбирать круглые или квадратные воздуховоды;
• Если места недостаточно (например, при реконструкции), выбирают прямоугольные воздуховоды. Как правило, ширина воздуховода в 2 раза больше высоты).

В таблице по горизонтальной указана высота воздуховода в мм, по вертикальной – его ширина, а в ячейках таблицы содержатся эквивалентные диаметры воздуховодов в мм.

Таблица эквивалентных диаметров воздуховодов

---

Смотрите также

• Децентрализованная система вентиляции
• Расценки на монтаж систем вентиляции
• Автоматизация систем вентиляции и кондиционирования воздуха
• Отключение аварийной вентиляции при пожаре
• Противопожарные клапана систем вентиляции
• Вытяжка на кухне с отводом в вентиляцию своими руками
• Подвал без вентиляции
• Вентиляция в стоматологии нормы
• Вентиляция в частном доме ванной комнаты
• Как устроена система вентиляции
• Схема вентиляции камеры покрасочной

Расчет местных сопротивлений в системах вентиляции | C.

O.K. archive | 2012

Рис. 1. Зависимость КМС унифицированных приточных тройников от величины

Такие потери пропорциональны динамическому давлению pд = ρv2/2, где ρ — плотность воздуха, равная примерно 1,2 кг/м3 при температуре около +20 °C, а v — его скорость [м/с], как правило, за сопротивлением. Коэффициенты пропорциональности ζ, называемые коэффициентами местного сопротивления (КМС), для различных элементов систем В и КВ обычно определяются по таблицам, имеющимся, в частности, в [2] и в ряде других источников.

Наибольшую сложность при этом чаще всего вызывает поиск КМС для тройников или узлов ответвлений, поскольку в этом случае необходимо принимать во внимание вид тройника (на проход или на ответвление) и режим движения воздуха (нагнетание или всасывание), а также отношение расхода воздуха в ответвлении к расходу в стволе Lo ʹ = Lo/Lc и площади сечения прохода к площади сечения ствола fn ʹ = fn/fc.

Для тройников при всасывании нужно учитывать еще и отношение площади сечения ответвления к площади сечения ствола fo ʹ = fo/fc. В руководстве [2] соответствующие данные приведены в табл. 22.36–22.40. Однако, при больших относительных расходах в ответвлении КМС меняются весьма резко, поэтому в этой области рассматриваемые таблицы вручную интерполируются с трудом и со значительной погрешностью.

Кроме того, в случае использования электронных таблиц MS Excel опять-таки желательно иметь формулы для непосредственного вычисления КМС через отношения расходов и сечений. При этом такие формулы должны быть, с одной стороны, достаточно простыми и удобными для массового проектирования и использования в учебном процессе, но, в то же время, не должны давать погрешность, превышающую обычную точность инженерного расчета.

Ранее подобная задача была решена автором применительно к сопротивлениям, встречающимся в водяных системах отопления [3]. Рассмотрим теперь данный вопрос для механических систем В и КВ. Ниже приведены результаты аппроксимации данных [2] для унифицированных тройников (узлов ответвлений) на проход. Общий вид зависимостей выбирался, исходя из физических соображений с учетом удобства пользования полученными выражениями при обеспечении допустимого отклонения от табличных данных:

• для приточных тройников, при Lo ʹ ≤ 0,7 и fn ʹ ≥ 0,5:
  
  а при Lo ʹ ≤ 0,4 можно пользоваться упрощенной формулой:
  
• для вытяжных тройников:
  
   

Нетрудно заметить, что относительная площадь прохода fn ʹ при нагнетании или соответственно ответвления fo ʹ при всасывании влияет на КМС одинаковым образом, а именно с увеличением fn ʹ или fo ʹ сопротивление будет уменьшаться, причем числовой коэффициент при указанных параметрах во всех приведенных формулах один и тот же, а именно (–0,25). Кроме того, и для приточных, и для вытяжных тройников при изменении расхода воздуха в ответвлении относительный минимум КМС имеет место при одинаковом уровне Lo ʹ = 0,2.

Данные обстоятельства говорят о том, что полученные выражения, несмотря на свою простоту, в достаточной мере отражают общие физические закономерности, лежащие в основе влияния исследуемых параметров на потери давления в тройниках любого типа. В частности, чем больше fn ʹ или fo ʹ, т.е. чем ближе они к единице, тем меньше меняется структура потока при прохождении сопротивления, а значит, и меньше КМС.

Для величины Lo ʹ зависимость является более сложной, но и здесь она будет общей обоих режимов движения воздуха. Представление о степени соответствия найденных соотношений и исходных значений КМС дает рис. 1, где показаны результаты обработки таблицы 22.37 для КМС унифицированных тройников (узлов ответвлений) на проход круглого и прямоугольного сечения при нагнетании. Примерно такая же картина получается и для аппроксимации табл. 22.38 с помощью формулы (3).

Заметим, что, хотя в последнем случае речь идет о круглом сечении, нетрудно убедиться, что выражение (3) достаточно удачно описывает и данные табл. 22.39, относящиеся уже к прямоугольным узлам. Погрешность формул для КМС в основном составляет 5–10 % (максимально до 15 %). Несколько более высокие отклонения может давать выражение (3) для тройников при всасывании, но и здесь это можно считать удовлетворительным с учетом сложности изменения сопротивления в таких элементах.

Во всяком случае, характер зависимости КМС от влияющих на него факторов здесь отражается очень хорошо. При этом полученные соотношения не требуют никаких иных исходных данных, кроме уже имеющихся в таблице аэродинамического расчета. В самом деле, в ней в явном виде должны быть указаны и расходы воздуха, и сечения на текущем и на соседнем участке, входящие в перечисленные формулы. Особенно это упрощает вычисления при использовании электронных таблиц MS Excel.

В то же время формулы, приведенные в настоящей работе, весьма просты, наглядны и легко доступны для инженерных расчетов, особенно в MS Excel, а также в учебном процессе. Их применение позволяет отказаться от интерполяции таблиц при сохранении точности, требуемой для инженерных расчетов, и непосредственно вычислять КМС тройников на проход при самых разнообразных соотношениях сечений и расходов воздуха в стволе и ответвлениях.

Этого вполне достаточно для проектирования систем В и КВ в большинстве жилых и общественных зданий.

Порядок расчета потерь давления в воздуховодах

Сердцем любой вентиляционной системы с механическим побуждением воздушного потока является вентилятор, который создает этот поток в воздуховодах. Мощность вентилятора напрямую зависит от напора, который необходимо создать на выходе из него, а для того, чтобы определить величину этого давления, требуется произвести расчет сопротивления всей системы каналов.

Для расчета потерь давления нужна схема и размеры воздуховода и дополнительного оборудования.

Исходные данные для вычислений

Когда известна схема вентиляционной системы, размеры всех воздухопроводов подобраны и определено дополнительное оборудование, схему изображают во фронтальной изометрической проекции, то есть аксонометрии. Если ее выполнить в соответствии с действующими стандартами, то на чертежах (или эскизах) будет видна вся информация, необходимая для расчета.

Аэродинамическая характеристика по вентилятора.

1. С помощью поэтажных планировок можно определить длины горизонтальных участков воздухопроводов. Если же на аксонометрической схеме проставлены отметки высот, на которых проходят каналы, то протяженность горизонтальных участков тоже станет известна. В противном случае потребуются разрезы здания с проложенными трассами воздухопроводов. И в крайнем случае, когда информации недостаточно, эти длины придется определять с помощью замеров по месту прокладки.
2. На схеме должно быть изображено с помощью условных обозначений все дополнительное оборудование, установленное в каналах. Это могут быть диафрагмы, заслонки с электроприводом, противопожарные клапаны, а также устройства для раздачи или вытяжки воздуха (решетки, панели, зонты, диффузоры). Каждая единица этого оборудования создает сопротивление на пути воздушного потока, которое необходимо учитывать при расчете.
3. В соответствии с нормативами на схеме возле условных изображений воздуховодов должны быть проставлены расходы воздуха и размеры каналов. Это определяющие параметры для вычислений.
4. Все фасонные и разветвляющие элементы тоже должны быть отражены на схеме.

Если такой схемы на бумаге или в электронном виде не существует, то придется ее начертить хотя бы в черновом варианте, при вычислениях без нее не обойтись.

Вернуться к оглавлению

С чего начинать?

Диаграмма потери напора на каждый метр воздуховода.

Очень часто приходится сталкиваться с достаточно простыми схемами вентиляции, в которых присутствует воздухопровод одного диаметра и нет никакого дополнительного оборудования. Такие схемы просчитываются достаточно просто, но что делать, если схема сложная с множеством ответвлений? Согласно методике просчета потерь давления в воздуховодах, которая изложена во многих справочных изданиях, нужно определить самую длинную ветвь системы либо ветку с наибольшим сопротивлением.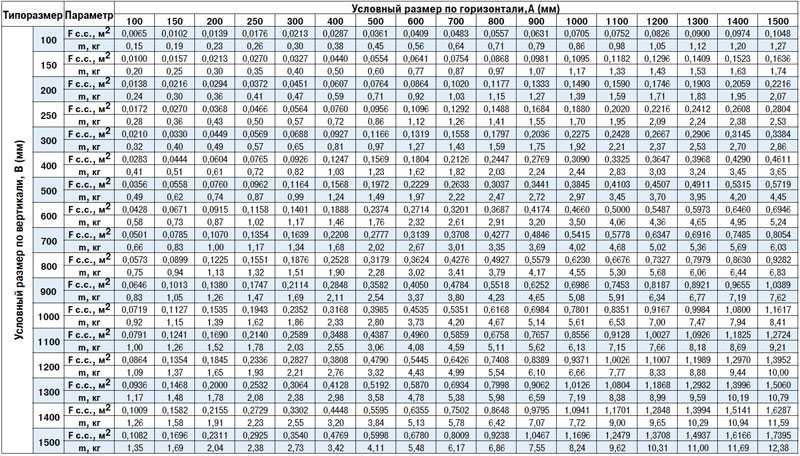 Выяснить таковую по сопротивлению на глаз удается редко, поэтому принято вести расчет по самой протяженной ветви. После этого пользуясь величинами расходов воздуха, проставленных на схеме, всю ветку делят на участки по этому признаку. Как правило, расходы меняются после разветвлений (тройников) и при делении лучше всего ориентироваться на них. Бывают и другие варианты, например, приточные или вытяжные решетки, встроенные прямо в магистральный воздуховод. Если на схеме это не показано, а такая решетка имеется, потребуется расход после нее высчитать. Участки нумеруют начиная от самого удаленного от вентилятора.

Вернуться к оглавлению

Порядок вычислений

Таблица максимальной скорости воздуха.

Общая формула расчета потерь давления в воздуховодах для всей вентиляционной системы выглядит следующим образом:

H_B = ∑(Rl + Z), где:

• H_B — потери давления во всей системе воздуховодов, кгс/м²;
• R — сопротивление трению 1 м воздухопровода эквивалентного сечения, кгс/м²;
• l — протяженность участка, м;
• Z — величина давления, теряемого воздушным потоком в местных сопротивлениях (фасонных элементах и дополнительном оборудовании).

Примечание: значение площади поперечного сечения воздуховода, участвующее в расчете, принимается изначально как для круглой формы канала. Сопротивление трению для каналов прямоугольной формы определяется по площади сечения, эквивалентному круглому.

Расчет начинают от самого отдаленного участка №1, затем переходят ко второму участку и так далее. Результаты вычислений по каждому участку складываются, о чем и говорит математический знак суммирования в расчетной формуле. Параметр R зависит от диаметра канала (d) и динамического давления в нем (Р_д), а последнее, в свою очередь, зависит от скорости движения воздушного потока. Коэффициент абсолютной шероховатости стенок (λ) традиционно принимается как для воздухопровода из оцинкованной стали и составляет 0,1 мм:

R = (λ / d) Р_д.

Диаграмма определения потерь напора и диаметра воздуховодов.

Пользоваться этой формулой в процессе расчета потерь давления не имеет смысла, так как значения R для различных скоростей воздуха и диаметров уже просчитаны и являются справочными величинами (Р. В. Щекин, И.Г. Староверов — справочники). Поэтому просто необходимо найти эти значения в соответствии с конкретными условиями перемещения воздушных масс и подставить их в формулу. Еще один показатель, динамическое давление Р_д, который связан с параметром R и участвует в дальнейшем подсчете местных сопротивлений, тоже величина справочная. Учитывая эту связь между двумя параметрами, в справочных таблицах они приводятся совместно.

Значение Z потерь давления в местных сопротивлениях рассчитывают по формуле:

Z = ∑ξ Р_д.

Знак суммирования обозначает, что нужно сложить результаты расчета по каждому из местных сопротивлений на заданном участке. Кроме уже известных параметров, в формуле присутствует коэффициент ξ. Его величина безразмерна и зависит от вида местного сопротивления. Значения параметра для многих элементов вентиляционных систем посчитаны либо определены опытным путем, поэтому находятся в справочной литературе. Коэффициенты местного сопротивления вентиляционного оборудования зачастую указывают сами производители, определив их значения опытным путем на производстве или в лаборатории.

Таблица эквивалентных диаметров воздуховодов.

Вычислив длину участка №1, количество и вид местных сопротивлений, следует правильно определить все параметры и подставить их в расчетные формулы. Получив результат, переходить ко второму участку и далее, до самого вентилятора. При этом не следует забывать о том участке воздухопровода, который расположен уже за вентиляционной установкой, ведь напора вентилятора должно хватить и на преодоление его сопротивления.

Закончив расчеты по самой протяженной ветви, производят такие же по соседней ветке, потом по следующей и так до самого конца. Обычно эти все ветви имеют много общих участков, поэтому вычисления пойдут быстрее. Целью определения потерь давления на всех ветвях есть их общая увязка, ведь вентилятор должен распределить свой расход равномерно по всей системе. То есть в идеале потери давления в одной ветви должны отличаться от другой не более чем на 10%. Простыми словами, это значит, что самое ближнее к вентилятору ответвление должно иметь самое высокое сопротивление, а дальнее — самое низкое. Если это не так, рекомендуется вернуться к пересчету диаметров воздуховодов и скоростей движения воздуха в них.

http://1poclimaty.ru/youtu.be/Ho2GXJgJIGI?t=14s

Когда по какой-либо причине увязать ветви невозможно, в них устанавливают дополнительные искусственные сопротивления — диафрагмы, которые следует подбирать. Для упрощения процесса вместо диафрагм устанавливают дроссель — клапаны, с их помощью можно сопротивление ветви регулировать, перекрывая поток заслонкой.

Как показывает практика, правильно просчитанная и отрегулированная после монтажа вентиляционная система работает безупречно.

Уравнение энергии – потеря давления в зависимости от потери напора

Полная энергия на единицу массы в данной точке потока жидкости состоит из энергии подъема (потенциальной), энергии скорости (кинетической) и энергии давления.

Уравнение энергии утверждает, что энергия не может исчезнуть – энергия выше по течению в потоке жидкости всегда будет равна энергии ниже по течению в потоке и потерям энергии между двумя точками.

E ₁ = E ₂ + E _убыток                              (1)

where

E ₁ = energy upstream (J/kg, Btu/lb)

E ₂ = Энергия ниже по течению (j/кг, BTU/LB)

E _Потеря = Потеря энергии _{. фунт)}

The energy in a specific point in the flow

E _flow = E _pressure + E _kinetic + E _potential                              (2)

where

E _{давление} = p/ ρ = энергия давления (Дж/кг, БТЕ/фунт)0009 = v ² / 2 = скорость (кинетическая) энергия (Дж/кг, БТЕ/фунт) /lb)

E _loss = Δ p _loss / ρ = major and minor energy loss in the fluid расход (Дж/кг, БТЕ/фунт)

P = давление в жидкости (PA (N/M ² ), PSI (LB/в ² )

Δ P _Loss = MARI незначительные потери давления в потоке жидкости (Па (Н/м ² ), фунт/кв. ³ )

v = скорость потока (м/с, фут/с)

g = ускорение свободного падения (м/с ² , фут/с ² )

ч = высота над уровнем моря (м, фут)

3 Eq 9. 1 и 2 можно объединить, чтобы выразить равные энергии в двух разных точках на линии тока как

p ₁ / ρ + v ₁ ² / 2 + 9000 = p ₂ / ρ + v ₂ ² / 2 + g h ₂ + Δp _loss / ρ                                      (3)

or alternatively

p ₁ + ρ v ₁ ² / 2 + ρ G H ₁ = P ₂ + ρ V ₂ ² /2 + ρ G H ₂ + ΔP _Потеря (3B)

Для горизонтального состояния (3B)

для горизонтального состояния (3B)

для горизонтального состояния (3B)

для0007 V ₁ = V ₂ и H ₁ = H ₂ , – и (3B) можно упростить до:

Δ P _Loss Δ P _{9000 9 Δ P 9 Δ P Δ P δ P Δ P 9 P 1 – P 2 (3C)}

Потеря давления делится на

• Основная потеря из -за Frict , клапаны и т. п.

Основные потери на трение в трубе или трубе зависят от скорости потока, длины трубы или воздуховода, диаметра трубы или воздуховода и коэффициента трения, основанного на шероховатости трубы или воздуховода, а также от того, является ли поток турбулентным или ламинарным – число Рейнольдса потока. Потеря давления в трубе или воздуховоде из-за трения, большая потеря, может быть выражена как:

Δ p _{major_loss} = λ (l/d _h ) (ρ v ² /2)                                  (4)

where

Δ p _{major_loss} = major friction pressure loss (Pa, (N/m ² ), lb/ft ² )

λ = Коэффициент трения

L = Длина протока или трубы (M, FT)

D _H = диаметр гидраулического диаметра (M, FT)

9032q32q. (3) также называют уравнением Д’Арси-Вейсбаха. (3) действителен для полностью развитого, устойчивого, несжимаемого потока.

Незначительные или динамические потери зависят от скорости потока, плотности и коэффициента для фактического компонента.

Δ p _{minor_loss} = ξ ρ v ² / 2                            (5)

where

Δ p _{minor_loss} = незначительная потеря давления (PA (N/M ² ), LB/FT ² )

ξ = Коэффициент незначительного потери

. Уравнение может быть выражено в терминах напора и потери напора путем деления каждого члена на удельный вес жидкости. Общий напор в потоке жидкости в трубе или воздуховоде может быть выражен как сумма напора по высоте, скоростного напора и напора.

Примечание ! Напоры в приведенных ниже уравнениях основаны на самой жидкости в качестве эталонной жидкости. Подробнее о голове читайте здесь.

P ₁ / γ + V ₁ ² /2 G + H ₁ = P ₂ / γ + V _{2 ² /2 G + H 2} + ΔH _Потеря (6)

, где

Δ H _потеря = потеря напора (м “жидкость”, футы “жидкость”)

γ = ρ g = удельный вес жидкости (Н/м 9017 фунт/фут 8, ³

3 )

для горизонтального потока устойчивого состояния V ₁ = V ₂ и P ₁ = P ₂ , – (4) можно преобразовать в

9099 , (4). ч _убыток = ч ₁ – H ₂ (6a)

, где

Δ H = P / γ = HEAD (M ”Fluid”, Ft “) 40014 40014 40014 (M” Fluid “, Ft”) (M “Fluid”.

Основная потеря головки трения в трубе или протоке из -за трения может быть выражена:

Δ H _{Major_loss} = λ (L / D _H ) (V ^{2 λ (L / D _H ) (V 2 λ (L / D _H ) (V 2 / 2 г) (7)}

, где

Δ H _Потеря = Потеря головки (M, FT)

коэффициент для фактической составляющей.

Δ P _{MINAL_LOSS} = ξ V ² / (2 G) (8)

Коэффициент трения –

λ

Коэффициент трения зависит от течения –

• ламинарного,
• переходного или
• турбулентного

и шероховатости трубы или воздуховода.

Чтобы определить коэффициент трения, мы сначала должны определить, является ли поток ламинарным, переходным или турбулентным, а затем использовать соответствующую формулу или диаграмму.

Коэффициент трения для ламинарного потока

Для полностью развитого ламинарного потока шероховатостью воздуховода или трубы можно пренебречь. Коэффициент трения зависит только от числа Рейнольдса – RE – и может быть выражен как:

λ = 64 / re (9)

, где

re = безразмерный reynolds №

28

– безразмерный reynolds number

92828

– безразмерный reynolds

92828

. ламинарный, когда Re < 2300

переходный, когда 2300 < Re < 4000

турбулентный, когда Re > 4000

Коэффициент трения для переходного течения

Если течение нестационарное – 2300 < Re < 4000 - течение колеблется между ламинарным и турбулентным течением, и коэффициент трения определить невозможно.

Коэффициент трения для турбулентного потока

Для турбулентного потока коэффициент трения зависит от числа Рейнольдса и шероховатости стенки воздуховода или трубы. В функциональной форме это можно выразить как:

λ = f( Re, k/d _h )                                       (10)

, где

K = Абсолютная шероховатость Стены трубки или протока (мм, фут)

K / D _H = 3333. или Грубая ROADIO – или Грубовая ROADIIO – или Грубая ROADIO – или Грубоярия – или Грубая грубая – или грубая.

Шероховатость материалов определяется опытным путем. Абсолютная шероховатость для некоторых распространенных материалов указана в таблице ниже

Поверхность	Абсолютная шероховатость – K
	(10 -3 M)	(футы)
СПКОП, LEAD, BRASTININIINIINIINIINIINIINIIN (NEW)
, LEAD, BRASTINIINIINIINIINIINIINIINIIN (новая)
, LEAD, BrASTININIINIINIINIINIINIINIIN (новая)
, LEAD, BrASTIN 10 -6
PVC and Plastic Pipes	0. 0015 – 0.007	0.5 – 2.33 10 -5
Epoxy, Vinyl Ester and Isophthalic pipe	0.005	1.7 10 -5
Stainless steel, bead blasted	0.001 – 0.006	(0.00328 – 0.0197) 10 -3
Stainless steel, turned	0.0004 – 0.006	(0.00131 – 0.0197) 10 – 3
нержавеющая сталь, электрополированная	0,0001 – 0,0008	(0,000328 – 0,00262) 10 -3
7 – 3
7 Стиль Стила.0751 1.5 – 3 10 -4
Stretched steel	0.015	5 10 -5
Weld steel	0.045	1.5 10 -4
Galvanized steel	0.15	5 10 -4
Rusted steel (corrosion)	0. 15 – 4	5 – 133 10 -4
New cast iron	0.25 – 0.8	8 – 27 10 -4
Чугун	0,8 – 1,5	2,7 – 5 10 -3
7 -3
7 -3
7 -3 . -3
Sheet or asphalted cast iron	0.01 – 0.015	3.33 – 5 10 -5
Smoothed cement	0.3	1 10 -3
Ordinary concrete	0.3 – 1	1 – 3.33 10 -3
Coarse concrete	0.3 – 5	1 – 16.7 10 -3
Well planed wood	0.18 – 0.9	6 – 30 10 -4
Ordinary wood	5	16.7 10 -3

The friction coefficient – λ – can be calculated by the Уравнение Коулбрука :

1 / λ ^1/2 = -2,0 log ₁₀ [ (2,51 / (Re λ ^1/2 )) + (k / d

8

8 ) / 3,72 ]                              (11)

Поскольку коэффициент трения – λ – находится в обеих частях уравнения, его необходимо решать путем итерации. Зная число Рейнольдса и шероховатость, можно рассчитать коэффициент трения λ в конкретном потоке.

Графическим представлением уравнения Коулбрука является диаграмма Муди :

• Диаграмма Муди – диаграмма Муди в формате для печати.

With the Moody diagram we can find the friction coefficient if we know the Reynolds Number – Re – and the

Relative Roughness Ratio – k / d _h

На диаграмме видно, как коэффициент трения зависит от числа Рейнольдса для ламинарного течения, как коэффициент трения не определен для переходного течения, и как коэффициент трения зависит от коэффициента шероховатости для турбулентного течения.

Для гидравлических гладких труб коэффициент шероховатости ограничивается нулем, а коэффициент трения более или менее зависит только от числа Рейнольдса.

Для полностью развитого турбулентного потока коэффициент трения зависит только от коэффициента шероховатости.

Пример – Потеря давления в воздуховодах

Воздух на 0 ^o C течет в 10 м оцинкованный воздуховод – 315 ​​мм диаметр – со скоростью 10 м/с 9.

Можно рассчитать число Рейнольдса:

RE = D _H V ρ / μ (12)

, где

RE = REYNOLDS №

V = VELOLDS.

ρ = density of air (kg/m ³ )

μ = dynamic or absolute viscosity ( Ns/m ² )

Расчетное число Рейнольдса:

Re = (15 м/с) (315 мм) (10 ^-3 м/мм ) (1,23 кг/м ³ ) / (1,79 10 ^-5 Ns/ M ² )

= 324679 (кгм/с ² )/n

= 324679 ~ турбулентный поток

Турбулентный поток указывает на то, что уравнение Colebrooks

. коэффициент трения – λ -.

С шероховатостью – ε – для оцинкованной стали 0,15 мм , можно рассчитать соотношение шероховатости:

Соотношение шероховатости = ε / D _H

= (0.159). мм)

    = 4,76 10 ^-4

Используя графическое представление уравнения Коулбрука – диаграмму Муди – коэффициент трения – λ – можно определить как:

λ = 0.017

The major loss for the 10 m duct can be calculated with the Darcy-Weisbach Equation (3) or (6):

Δp _потери = λ ( l / d _h ) ( ρ v ² / 2 )

= 0,017 ((10 м) / (0,315 м)) ( (1,23 кг/м 3 90 ^{) (15 м/с) 2 / 2 )}

= 74 Па (Н/м ² )

Формула расчета перепада давления в трубопроводе, теория и уравнения

Когда жидкость течет по трубе, возникает падение давления из-за сопротивления потоку. Также может иметь место прирост/потеря давления из-за изменения высоты между началом и концом трубы. Эта общая разница давлений в трубе связана с рядом факторов:

• Трение между жидкостью и стенкой трубы
• Трение между соседними слоями самой жидкости
• Потери на трение при прохождении жидкости через любые трубопроводные фитинги, изгибы, клапаны или компоненты
• Потеря давления из-за изменения высоты жидкости (если труба не горизонтальна)
• Повышение давления из-за любого напора жидкости, добавляемого насосом

Расчет перепада давления в трубе

Для расчета потери давления в трубе необходимо вычислить падение давления, обычно в напоре жидкости, для каждого из элементов, вызывающих изменение давления. Однако для расчета потерь на трение, например, в трубе, необходимо рассчитать коэффициент трения, чтобы использовать его в уравнении Дарси-Вейсбаха, которое определяет общие потери на трение.

Сам коэффициент трения зависит от внутреннего диаметра трубы, внутренней шероховатости трубы и числа Рейнольдса, которое, в свою очередь, рассчитывается на основе вязкости жидкости, плотности жидкости, скорости жидкости и внутреннего диаметра трубы.

Таким образом, для расчета общих потерь на трение необходимо выполнить ряд промежуточных расчетов. Работая в обратном направлении, мы должны знать свойства плотности и вязкости жидкости, знать диаметр трубы и свойства шероховатости, вычислить число Рейнольдса, использовать это для расчета коэффициента трения с помощью уравнения Коулбрука-Уайта и, наконец, подставить коэффициент трения в уравнение Дарси. Уравнение Вейсбаха для расчета потерь на трение в трубе.

После расчета потерь на трение в трубе нам необходимо учесть возможные потери на фитингах, изменение высоты и любой добавленный напор насоса. Суммируя эти потери/приросты, мы получим общее падение давления в трубе. В следующих разделах каждый расчет рассматривается по очереди.

Расчет потерь на трение в трубах

Теперь нам нужно рассчитать каждый из элементов, необходимых для определения потерь на трение в трубе. Ссылки в следующем списке содержат более подробную информацию о каждом конкретном расчете:

• Плотность жидкости
• Вязкость жидкости
• Измерение шероховатости труб
• Число Рейнольдса — ламинарное или турбулентное течение
• Коэффициенты трения — диаграмма Муди и уравнение Коулбрука-Уайта
• Потери на трение в трубе – метод Дарси-Вейсбаха

Наше программное обеспечение Pipe Flow автоматически рассчитывает потери на трение в трубах с использованием уравнения Дарси-Вейсбаха, поскольку это наиболее точный метод расчета для несжимаемых жидкостей, а также он считается точным в отрасли для потока сжимаемых жидкостей при соблюдении определенных условий.

Расчет потерь на трубных фитингах

Потери энергии из-за клапанов, фитингов и изгибов вызваны некоторым локальным нарушением потока. Рассеивание потерянной энергии происходит на конечном, но не обязательно коротком участке трубопровода, однако для гидравлических расчетов принято считать всю величину этих потерь в месте расположения устройства.

Для трубопроводных систем с относительно длинными трубами часто бывает так, что потери на фитингах будут незначительными по сравнению с общими потерями давления в трубе. Однако некоторые локальные потери, например, вызванные частично открытым клапаном, часто очень значительны и никогда не могут быть названы незначительными потерями, и их всегда следует учитывать.

Потери, создаваемые конкретным фитингом, измеряются с использованием реальных экспериментальных данных, а затем анализируются для определения коэффициента К (коэффициент локальных потерь), который можно использовать для расчета потерь в фитингах, поскольку они зависят от скорости прохождения жидкости. через это.

Наши программы Pipe Flow Software позволяют легко автоматически включать потери в фитингах и другие локальные потери в расчет перепада давления, поскольку они поставляются с предварительно загруженной базой данных фитингов, которая содержит множество отраслевых стандартных коэффициентов K для различных клапанов и фитингов различных размеров. .

Все, что нужно сделать пользователю, это выбрать соответствующий фитинг или клапан, а затем выбрать «Сохранить», чтобы добавить его к трубе и включить в расчет потери давления в трубе.

Эта ссылка содержит дополнительную информацию о факторах К фитинга и уравнении потерь фитинга.

Расчет потерь компонентов трубопровода

Часто в системе трубопроводов необходимо смоделировать множество различных типов компонентов, таких как теплообменник или чиллер. Некоторые компоненты могут вносить известную фиксированную потерю давления, однако более вероятно, что падение давления будет меняться в зависимости от скорости потока, проходящего через компонент.

Большинство производителей предоставляют кривую производительности компонентов, которая описывает характеристики расхода и потери напора их продукта. Затем эти данные используются для расчета потери давления, вызванной компонентом, для заданного расхода, но сам расход также будет зависеть от потери давления после компонента, поэтому очень сложно смоделировать характеристики потери напора компонента без использование соответствующего программного обеспечения, такого как Pipe Flow Expert.

Потеря давления из-за изменения высоты

Поток в восходящей трубе

Если начальная отметка трубы ниже конечной, то помимо трения и других потерь будет дополнительная потеря давления, вызванная подъемом, которая измеряется в напоре жидкости и просто эквивалентна подъему.

т. е. при более высокой высоте жидкости добавляется меньшее давление из-за меньшей глубины и веса жидкости над этой точкой.

Поток в падающей трубе

Если начальная отметка трубы выше конечной, то наряду с трением и другими потерями будет дополнительный прирост давления, вызванный перепадом высоты, который измеряется в напоре жидкости и просто эквивалентен падению отметки.

то есть при более низком уровне жидкости создается большее давление из-за увеличения глубины и веса жидкости над этой точкой.

Энергетические и гидравлические классы

Подъем жидкости в трубе вместе с давлением в трубе в определенной точке и скоростным напором жидкости можно суммировать для расчета так называемой линии энергетического класса.

Линия гидравлического класса может быть рассчитана путем вычитания скоростного напора жидкости из EGL (линия уровня энергии) или просто путем суммирования только высоты жидкости и давления в трубе в этой точке.

Расчет напора насоса

В системе трубопроводов часто есть насос, который создает дополнительное давление (известное как «напор насоса») для преодоления потерь на трение и других сопротивлений. Производительность насоса обычно доступна у производителя в виде кривой производительности насоса, которая представляет собой график зависимости расхода от напора, создаваемого насосом, для диапазона значений расхода.

Поскольку напор, создаваемый насосом, зависит от расхода, определение рабочей точки на кривой производительности насоса не всегда является легкой задачей. Если вы угадаете скорость потока, а затем рассчитаете добавленный напор насоса, это, в свою очередь, повлияет на разницу давлений в трубе, которая сама по себе повлияет на скорость потока.

Конечно, если вы используете наше программное обеспечение Pipe Flow Expert, оно найдет для вас точную рабочую точку на кривой насоса, гарантируя баланс потоков и давлений во всей вашей системе, чтобы дать точное решение для вашей конструкции трубопровода.

Как бы вы ни рассчитывали напор насоса, добавленный в вашу трубу, этот дополнительный напор жидкости должен быть добавлен обратно к любому падению давления, которое произошло в трубе.

Расчет падения давления в трубе

Таким образом, давление на конце рассматриваемой трубы определяется следующим уравнением (где все элементы указаны в м напора жидкости):

P[конец] = P[начало] – Потери на трение – Потери в фитингах – Потери на компонентах + Высота [начало-конец] + Напор насоса

где

P[end] = Давление на конце трубы
P[start] = Давление в начале трубы
Высота[начало-конец] = (Отметка в начале трубы) – (Отметка в конце трубы)
Напор насоса = 0, если насос отсутствует

Таким образом, падение давления или, скорее, перепад давления dP (это может быть усиление) между началом и концом трубы задается следующим уравнением:

dP = Потери на трение + Потери в фитингах + Потери на компонентах – Высота [начало-конец] – Напор насоса

где

P[end] = Давление на конце трубы
P[start] = Давление в начале трубы
Высота[начало-конец] = (Отметка в начале трубы) – (Отметка в конце трубы)
Напор насоса = 0, если насос отсутствует

Примечание dP обычно задается как положительное значение, относящееся к падению давления. Отрицательное значение указывает на прирост давления.

Потери энергии в трубах – Лабораторное руководство по прикладной гидромеханике

Общие потери энергии в трубопроводной системе представляют собой сумму основных и второстепенных потерь. Основные потери связаны с потерями энергии на трение, вызванными вязким воздействием жидкости и шероховатостью стенки трубы. Большие потери создают перепад давления вдоль трубы, так как давление должно работать, чтобы преодолеть сопротивление трения. Уравнение Дарси-Вейсбаха является наиболее широко принятой формулой для определения потерь энергии при течении в трубе. В этом уравнении коэффициент трения ( f ), безразмерная величина, используется для описания потерь на трение в трубе. В ламинарных потоках f  является функцией только числа Рейнольдса и не зависит от шероховатости поверхности трубы. В полностью турбулентных течениях f зависит как от числа Рейнольдса, так и от относительной шероховатости стенки трубы. В инженерных задачах f определяется с помощью диаграммы Муди.

В инженерных приложениях важно повысить производительность трубы, т. е. максимально увеличить пропускную способность и минимизировать потери напора на единицу длины. Согласно уравнению Дарси-Вейсбаха, при заданном расходе потери напора уменьшаются с обратной пятой степенью диаметра трубы. Удвоение диаметра трубы приводит к уменьшению потери напора в 32 раза (≈ 9снижение на 7%), а количество требуемого материала на единицу длины трубы и стоимость ее монтажа почти удваиваются. Это означает, что потребление энергии для преодоления сопротивления трения в трубе, транспортирующей определенный расход, может быть значительно снижено при относительно небольших капитальных затратах.

Целью этого эксперимента является исследование потери напора из-за трения в трубе и определение связанного с этим коэффициента трения при различных расходах и режимах потока, т. е. ламинарном, переходном и турбулентном.

Коэффициент трения определяется путем измерения разницы напора между двумя фиксированными точками в прямой трубе с круглым поперечным сечением для установившихся потоков.

Для проведения эксперимента по потерям энергии в трубах требуется следующее оборудование:

• Гидравлический стол F1-10,
• Аппарат трения трубы Ф1-18,
• Секундомер для измерения расхода,
• Мерный цилиндр для измерения очень малых расходов,
• спиртовой уровень и
• Термометр.

Аппарат трения труб состоит из испытательной трубы (установленной вертикально на буровой установке), резервуара постоянного напора, клапана регулирования расхода, клапана стравливания воздуха и двух комплектов манометров для измерения потерь напора в трубе (рис. 4.1). ). Набор из двух водортутных манометров используется для измерения больших перепадов давления, а два водяных манометра используются для измерения малых перепадов давления. Когда манометры не используются, их можно изолировать с помощью зажимов Хоффмана.

Поскольку ртуть считается опасным веществом, ее нельзя использовать в лабораториях гидромеханики для студентов бакалавриата. Поэтому для этого эксперимента ртутные манометры заменены дифференциальным манометром для непосредственного измерения больших перепадов давления.

Этот эксперимент проводится при двух условиях потока: высокий расход и низкий расход. Для экспериментов с высокой скоростью потока входная труба подключается непосредственно к водопроводу стенда. Для экспериментов с низким расходом вход в бак постоянного напора соединяется с подачей стенда, а выход в основании напорного бака соединяется с верхней частью испытательной трубы [4].

Клапан управления потоком аппарата используется для регулирования потока через тестовую трубу. Этот клапан должен быть обращен к объемному резервуару, и к нему должен быть присоединен короткий отрезок гибкой трубки, чтобы предотвратить разбрызгивание.

Воздушный клапан облегчает продувку системы и регулировку уровня воды в водяных манометрах до удобного уровня, пропуская в них воздух.

Рисунок 4.1: Устройство для испытания труб на трение F1-18

Потери энергии в трубе можно определить, применив уравнение энергии к отрезку прямой трубы с однородным поперечным сечением:

Если труба горизонтальная: 

Начиная с v _in = v _{out :}

Разность давлений (P _из -P _из ) между двумя точками в трубе обусловлена ​​сопротивлением трению, а потеря напора ч _L прямо пропорциональна разности давлений.

Потеря напора из-за трения может быть рассчитана по уравнению Дарси-Вейсбаха:

где:

: потеря напора из-за сопротивления потоку

f:    Коэффициент Дарси-Вейсбаха

L: длина трубы

D: диаметр трубы

v : средняя скорость

g: гравитационное ускорение.

Для ламинарного потока коэффициент Дарси-Вейсбаха (или коэффициент трения f ) зависит только от числа Рейнольдса (Re) и не зависит от шероховатости поверхности трубы, т. е.:

Для турбулентного потока f  является функцией как числа Рейнольдса, так и высоты шероховатости трубы, . Другие факторы, такие как расстояние между шероховатостями и форма, также могут влиять на значение f ; однако эти эффекты недостаточно изучены, и во многих случаях ими можно пренебречь. Следовательно, f должны быть определены экспериментально. Диаграмма Муди связывает f с относительной шероховатостью стенки трубы (/D) и числом Рейнольдса (рис. 4.2).

Вместо использования диаграммы Муди f можно определить, используя эмпирические формулы. Эти формулы используются в инженерных приложениях, когда используются компьютерные программы или методы расчета в электронных таблицах. Для турбулентного потока в гладкой трубе хорошо известная кривая, соответствующая диаграмме Муди, имеет вид:

Число Рейнольдса определяется как:

, где v — средняя скорость, D — диаметр трубы, а и — динамическая и кинематическая вязкости жидкости соответственно. (Рисунок 4.3).

В этом эксперименте h _L измеряется непосредственно с помощью водяных манометров и дифференциального манометра, которые соединены отводами давления с испытательной трубой. Средняя скорость, v , ​​вычисляется из объемного расхода (Q) как:

В соответствующих расчетах могут быть использованы следующие размеры испытательной трубы [4]: ​​

Длина испытательной трубы = 0,50 м,

Диаметр испытательной трубы = 0,003 м.

Рисунок 4.2: Диаграмма Муди Рисунок 4.3: Кинематическая вязкость воды (v) при атмосферном давлении

• Установите испытательный стенд на гидравлическом стенде и отрегулируйте ножки с помощью спиртового уровня, чтобы убедиться, что опорная плита находится в горизонтальном положении, а манометры — в вертикальном положении.
• Присоедините зажимы Хоффмана к водяным манометрам и соединительным трубкам манометров и закройте их.

Эксперимент с высокой скоростью потока

Высокий расход будет подаваться в испытательную секцию путем подсоединения впускной трубы оборудования к гидравлическому стенду при выключенном насосе. Следует выполнить следующие шаги.

• Закройте клапан стенда, полностью откройте клапан управления потоком аппарата и запустите насос. Постепенно открывайте клапан скамьи и запускайте поток, пока весь воздух не будет удален.
• Снимите хомуты с соединительных трубок манометра перепада давления и удалите весь воздух из клапана выпуска воздуха, расположенного сбоку манометра.
• Закройте клапан для выпуска воздуха, как только в соединительных трубках перестанут появляться пузырьки воздуха.
• Закройте клапан управления расходом аппарата и снимите показания нулевого расхода с манометра.
• При полностью открытом клапане управления потоком измерьте потери напора, показанные манометром.
• Определите скорость потока путем сбора по времени.
• Отрегулируйте клапан управления потоком ступенчато, чтобы наблюдать перепады давления с шагом 0,05 бар. Получите данные для десяти скоростей потока. Для каждого шага определите скорость потока по времени сбора.
• Закройте клапан управления потоком и выключите насос.

Разность давлений, измеренная дифференциальным манометром, может быть преобразована в эквивалентную потерю напора (ч _L ) с использованием коэффициента преобразования:

1 бар = 10,2 м водяного столба

Эксперимент с низким расходом

Низкий расход будет подаваться в испытательную секцию путем подсоединения выпускной трубы стенда гидравлики к напорному баку при выключенном насосе. Выполните следующие шаги.

• Прикрепите хомут к каждому разъему манометра перепада давления и закройте их.
• Отсоедините подводящую трубку тестовой трубки и держите ее высоко, чтобы она оставалась заполненной водой.
• Подсоедините трубку подачи скамьи к входу напорного резервуара, запустите насос и откройте клапан скамьи, чтобы обеспечить поток. Когда происходит утечка из защелкивающегося соединителя напорного резервуара, подсоедините к нему трубку подачи тестовой секции, убедившись, что воздух не захвачен.
• Когда происходит утечка из-за переполнения напорного бака, полностью откройте регулирующий клапан.
• Снимите хомуты с трубок водяных манометров и закройте регулирующий клапан.
• Подсоедините отрезок трубки малого диаметра от воздушного клапана к мерному резервуару, откройте винт для выпуска воздуха и дайте потоку пройти через манометры, чтобы удалить из них весь воздух. Затем затяните винт для выпуска воздуха.
• Полностью откройте регулирующий клапан и медленно откройте клапан для выпуска воздуха, позволяя воздуху поступать до тех пор, пока уровни манометров не достигнут удобной высоты (посередине манометров), затем закройте вентиляционное отверстие. При необходимости можно дополнительно контролировать уровни, используя ручной насос для повышения давления воздуха на манометре.
• При полностью открытом клапане управления потоком измерьте потери напора, показанные манометрами.
• Определите скорость потока путем сбора по времени.
• Получите данные не менее чем для восьми скоростей потока, самая низкая из которых даст h _L = 30 мм.
• Измерьте температуру воды с помощью термометра.

Используйте эту ссылку для доступа к рабочей книге Excel для этого эксперимента.

9.1. Результаты

Запишите все показания манометра и манометра, температуру воды и объемные измерения в таблицы необработанных данных.

Таблицы необработанных данных: Эксперимент с высокой скоростью потока

Тест №	Потеря напора (бар)	Объем (литры)	Время (с)
1
2
3
4
5
6
7
8
9
10

Таблицы исходных данных: Эксперимент с низким расходом

Тест №	ч 1 (м)	ч 2 (м)	Потеря напора ч л (м)	Объем (литры)	Время (с)
1
2
3
4
5
6
7
8
Температура воды:

9. 2. Расчеты

Расчет значений разряда; средняя скорость потока; и экспериментальный коэффициент трения, f с использованием уравнения 3, и число Рейнольдса для каждого эксперимента. Кроме того, рассчитайте теоретический коэффициент трения, f , используя уравнение 4 для ламинарного потока и уравнение 5 для турбулентного потока для диапазона чисел Рейнольдса. Запишите свои расчеты в следующие образцы таблиц результатов.

Таблица результатов — экспериментальные значения

Тест №	Потеря напора ч л (м)	Объем (литры)	Время (с)	Расход (м 3 /с)	Скорость (м/с)	Коэффициент трения, f	Номер Рейнольдса
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

Таблица результатов – теоретические значения

№	Режим потока	Номер Рейнольдса	Коэффициент трения, f
1	Ламинарный (уравнение 4)	100
2		200
3		400
4		800
5		1600
6		2000
7	Турбулентность (уравнение 5)	4000
8		6000
9		8000
10		10000
11		12000
12		16000
13		20000

Используйте предоставленный шаблон для подготовки лабораторного отчета для этого эксперимента. Ваш отчет должен включать следующее:

• Таблица(и) исходных данных
• Таблицы результатов
• График(и)
  • На одном графике нанесите экспериментальные и теоретические значения коэффициента трения f (ось Y) в зависимости от числа Рейнольдса, Re (ось x) в логарифмической шкале. Экспериментальные результаты следует разделить на три группы (ламинарные, переходные и турбулентные) и нанести на них отдельно. Теоретические значения следует разделить на две группы (ламинарные и турбулентные) и также нанести на них отдельно.
  • На одном графике постройте h _L (ось Y) в зависимости от средней скорости потока, v (ось x) в логарифмическом масштабе.

• Обсудите следующее:
  • Определите ламинарный и турбулентный режимы течения в своем эксперименте. Каково критическое число Рейнольдса в этом эксперименте (т. е. переходное число Рейнольдса от ламинарного течения к турбулентному)?
  • Предполагая соотношение в форме , рассчитайте значения K и n из графика экспериментальных данных, которые вы построили, и сравните их с принятыми значениями, показанными в разделе «Теория» (уравнения 4 и 5).