Расчет местных сопротивлений в системах вентиляции | C.O.K. archive | 2012
Рис. 1. Зависимость КМС унифицированных приточных тройников от величины
Такие потери пропорциональны динамическому давлению pд = ρv2/2, где ρ — плотность воздуха, равная примерно 1,2 кг/м3 при температуре около +20 °C, а v — его скорость [м/с], как правило, за сопротивлением. Коэффициенты пропорциональности ζ, называемые коэффициентами местного сопротивления (КМС), для различных элементов систем В и КВ обычно определяются по таблицам, имеющимся, в частности, в [2] и в ряде других источников.
Наибольшую сложность при этом чаще всего вызывает поиск КМС для тройников или узлов ответвлений, поскольку в этом случае необходимо принимать во внимание вид тройника (на проход или на ответвление) и режим движения воздуха (нагнетание или всасывание), а также отношение расхода воздуха в ответвлении к расходу в стволе Lo ʹ = Lo/Lc и площади сечения прохода к площади сечения ствола fn ʹ = fn/fc.
Для тройников при всасывании нужно учитывать еще и отношение площади сечения ответвления к площади сечения ствола fo ʹ = fo/fc.
Кроме того, в случае использования электронных таблиц MS Excel опять-таки желательно иметь формулы для непосредственного вычисления КМС через отношения расходов и сечений. При этом такие формулы должны быть, с одной стороны, достаточно простыми и удобными для массового проектирования и использования в учебном процессе, но, в то же время, не должны давать погрешность, превышающую обычную точность инженерного расчета.
Ранее подобная задача была решена автором применительно к сопротивлениям, встречающимся в водяных системах отопления [3]. Рассмотрим теперь данный вопрос для механических систем В и КВ. Ниже приведены результаты аппроксимации данных [2] для унифицированных тройников (узлов ответвлений) на проход. Общий вид зависимостей выбирался, исходя из физических соображений с учетом удобства пользования полученными выражениями при обеспечении допустимого отклонения от табличных данных:
- для приточных тройников, при Lo ʹ ≤ 0,7 и fn ʹ ≥ 0,5:
а при Lo ʹ ≤ 0,4 можно пользоваться упрощенной формулой: - для вытяжных тройников:
Нетрудно заметить, что относительная площадь прохода fn ʹ при нагнетании или соответственно ответвления fo ʹ при всасывании влияет на КМС одинаковым образом, а именно с увеличением fn ʹ или fo ʹ сопротивление будет уменьшаться, причем числовой коэффициент при указанных параметрах во всех приведенных формулах один и тот же, а именно (–0,25).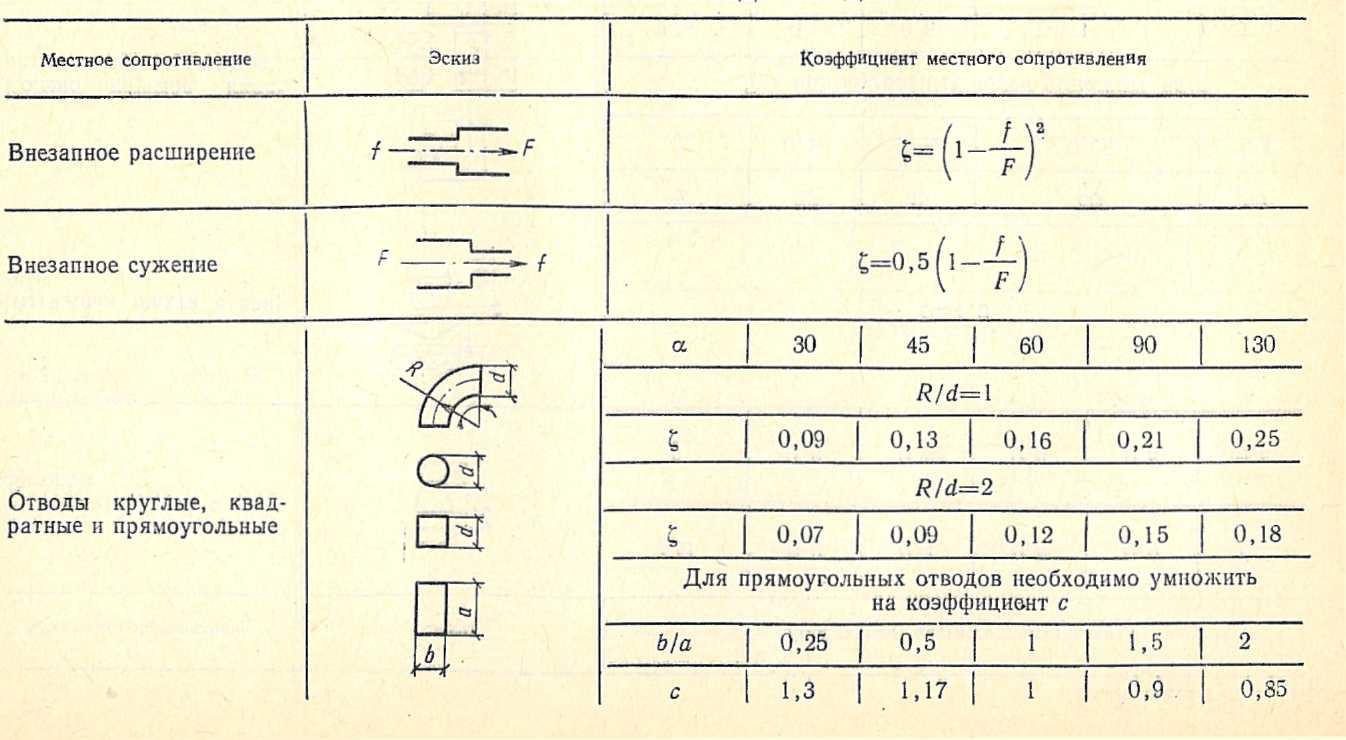
Кроме того, и для приточных, и для вытяжных тройников при изменении расхода воздуха в ответвлении относительный минимум КМС имеет место при одинаковом уровне Lo ʹ = 0,2.
Данные обстоятельства говорят о том, что полученные выражения, несмотря на свою простоту, в достаточной мере отражают общие физические закономерности, лежащие в основе влияния исследуемых параметров на потери давления в тройниках любого типа. В частности, чем больше fn ʹ или fo ʹ, т.е. чем ближе они к единице, тем меньше меняется структура потока при прохождении сопротивления, а значит, и меньше КМС.
Для величины Lo ʹ зависимость является более сложной, но и здесь она будет общей обоих режимов движения воздуха. Представление о степени соответствия найденных соотношений и исходных значений КМС дает рис. 1, где показаны результаты обработки таблицы 22.37 для КМС унифицированных тройников (узлов ответвлений) на проход круглого и прямоугольного сечения при нагнетании. Примерно такая же картина получается и для аппроксимации табл.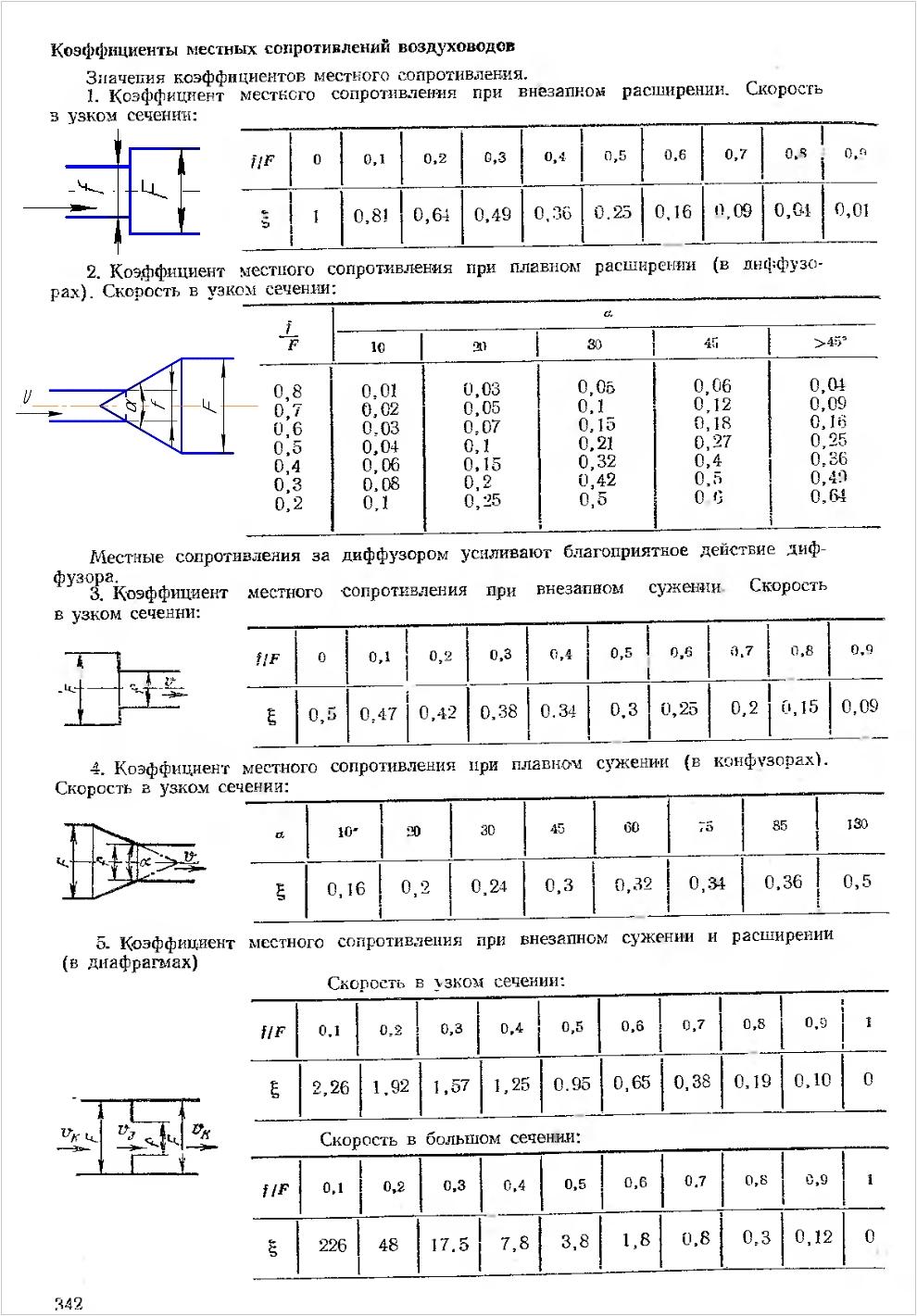
Заметим, что, хотя в последнем случае речь идет о круглом сечении, нетрудно убедиться, что выражение (3) достаточно удачно описывает и данные табл. 22.39, относящиеся уже к прямоугольным узлам. Погрешность формул для КМС в основном составляет 5–10 % (максимально до 15 %). Несколько более высокие отклонения может давать выражение (3) для тройников при всасывании, но и здесь это можно считать удовлетворительным с учетом сложности изменения сопротивления в таких элементах.
Во всяком случае, характер зависимости КМС от влияющих на него факторов здесь отражается очень хорошо. При этом полученные соотношения не требуют никаких иных исходных данных, кроме уже имеющихся в таблице аэродинамического расчета. В самом деле, в ней в явном виде должны быть указаны и расходы воздуха, и сечения на текущем и на соседнем участке, входящие в перечисленные формулы. Особенно это упрощает вычисления при использовании электронных таблиц MS Excel.
В то же время формулы, приведенные в настоящей работе, весьма просты, наглядны и легко доступны для инженерных расчетов, особенно в MS Excel, а также в учебном процессе.
Их применение позволяет отказаться от интерполяции таблиц при сохранении точности, требуемой для инженерных расчетов, и непосредственно вычислять КМС тройников на проход при самых разнообразных соотношениях сечений и расходов воздуха в стволе и ответвлениях.
Этого вполне достаточно для проектирования систем В и КВ в большинстве жилых и общественных зданий.
Расчет потерь давления на противопожарных клапанах
- Расчет потерь давления
Расчет потерь давления на противопожарных нормально открытых клапанах систем общеобменной вентиляции и кондиционирования.
Являясь обязательными элементами систем общеобменной вентиляции и кондиционирования, противопожарные НО (огнезадерживающие) клапаны в нормальных условиях функционирования вентиляционных систем открыты и представляют собой дополнительное местное сопротивление проходящему через них воздуху. Величина потерь давления на НО клапанах зависит от толщины теплоизолированной створки и конструктивных особенностей внутренних элементов изделия, влияющих как на проходное (живое) сечение клапана, так и на условия обтекания этих элементов воздухом.
Потери давления на канальных противопожарных НО клапанах КПВ.01(02,03), КДД.01 могут быть рассчитаны о формуле:
ΔPкл = ζв ρв (Vв)2 / 2, Па;
где:
ζв – коэффициент местного сопротивления (КМС) клапана, отнесенный к скорости воздуха в воздуховоде;
ρв – плотность воздуха, кг/м³
Vв – скорость воздуха в воздуховоде, м/с.
Значения ζв для всех указанных типов клапанов представлены в соответствующих разделах каталога.
Расчет потерь давления на противопожарных нормально закрытых, в т. ч. дымовых, клапанах систем противодымной вентиляции
Потери давления в открытых клапанах стенового типа КДВ.01, КПВ.01(02) и КПВ.03, установленных в системах вытяжной противодымной вентиляции (системах дымоудаления) могут быть рассчитаны по формуле:
ΔPкл = ζкл ρд (Vкл)2 / 2, Па;
где:
ζкл – коэффициент местного сопротивления, отнесенный к скорости в проходном сечении клапана;
ρд – плотность дыма, кг/м³
Vкл – скорость дыма в проходном сечении клапана, м/с.
Потери давления ΔPкл в данном случае представляют собой суммарные потери давления на начальном участке сети дымоудаления, определяемые при проведении аэродинамического расчета.
Потери давления ΔPкл могут быть рассчитаны через массовую скорость дыма в проходном сечении клапана следующим образом:
ΔPкл = ζкл (Vкл ρд )2 / (2ρд), Па;
Значения ζкл принимаются по таблицам (см. разделы) в зависимости от характеристики входного элемента сети дымоудаления.
Потери давления в канальных НЗ (дымовых) клапанах КДВ.01, КПВ.01(02,03), установленных в каналах вытяжных систем противодымной вентиляции, могут быть рассчитаны по формуле:
ΔPкл = ζв ρд (Vв )2 / 2, Па;
Потери давления в «канальных» НЗ клапанах КДВ.01, КПВ.
ΔPкл = ζв ρв (Vв )2 / 2, Па;
При установке «канальных» клапанов на входе или выходе приточно-вытяжных систем противодымной вентиляции следует дополнительно учитывать потери давления входа (выхода) потока газа.
.
Нужен совет?
Сложно определиться с выбором – напишите нам на почту
Задать вопрос
Помочь найти?
Не нашли то, что искали – воспользуйтесь поиском
Новинки
Обновление ассортимента уже здесь, на нашем сайте!
Смотреть новинки
Уравнение энергии – потеря давления в зависимости от потери напора
Полная энергия на единицу массы в данной точке потока жидкости состоит из энергии подъема (потенциальной), энергии скорости (кинетической) и энергии давления.
Уравнение энергии утверждает, что энергия не может исчезнуть – энергия выше по течению в потоке жидкости всегда будет равна энергии ниже по течению в потоке и потерям энергии между двумя точками.
E 1 = E 2 + E убыток (1)
где
E 1 = энергия вверх по течению (Дж/кг, БТЕ/фунт)
Е 2 = энергия ниже по течению E потери = потери энергии (Дж/кг, БТЕ/ фунт)
Энергия в конкретной точке потока
E расход = E давление + E кинетика 90 009 + E потенциал (2)
, где
E давление = p / ρ = энергия давления (Дж/кг, БТЕ/фунт)
E потенциал ) энергия (Дж/кг, БТЕ /lb)
E потеря = Δ p потеря 90 007 / ρ = большие и малые потери энергии в жидкости расход (Дж/кг, БТЕ/фунт)
p = давление жидкости (Па (Н/м 2 ), фунт/кв.
дюйм (фунт/дюйм 2 ))
9 0007 Δ p потеря = основная и незначительные потери давления в потоке жидкости (Па (Н/м 2 ), фунт/кв. 3 )
v = скорость потока (м/с, фут/с)
г = ускорение свободного падения (м/с 2 , фут/с 2 )
ч = высота над уровнем моря (м, фут) 90 003
Экв. 1 и 2 можно объединить, чтобы выразить равные энергии в двух разных точках на линии тока как
p 1 / ρ + v 1 2 / 2 + г ч 1 = p 2 / ρ + v 2 2 / 2 + g h 2 + Δp потери / ρ 007
p 1 + ρ v 1 2 / 2 + ρ g h 1 = p 2 + ρ v 2 2 / 2 + ρ g h 2 + Δp потеря (3b)
Для горизонтального установившегося течения v 1 = v 2 и h 1 = h 2 , – и (3b) можно упростить до:
9030 9Δ р потеря = p 1 – p 2 (3c)
Потери давления делятся на
- большие потери из-за трения и
- незначительные потери из-за изменения скорости в поворотах , клапаны и т.
п.
п.Основные потери на трение в трубе или трубе зависят от скорости потока, длины трубы или воздуховода, диаметра трубы или воздуховода и коэффициента трения, основанного на шероховатости трубы или воздуховода, а также от того, является ли поток турбулентным или ламинарным – число Рейнольдса потока. Потеря давления в трубе или воздуховоде из-за трения, большая потеря, может быть выражена как:
Δ p major_loss = λ (l/d h ) (ρ v 2 /2) (4)
где
Δ p главные_потери = потеря давления на трение (Па, (Н/м ) 2 ), фунт/фут 2 )
λ = коэффициент трения
l = длина воздуховода или трубы (м, фут)
d h = гидравлический диаметр (м, фут)
Ур.
(3) также называют уравнением Д’Арси-Вейсбаха. (3) действителен для полностью развитого, устойчивого, несжимаемого потока.
Незначительные или динамические потери зависят от скорости потока, плотности и коэффициента для фактического компонента.
Δ p незначительные_потери = ξ ρ v 2 / 2 (5)
где
Δ p незначительные_потери = незначительная потеря давления (Па (Н/м 2 ), фунт/фут 2 )
ξ = коэффициент незначительной потери 900 14
Напор и потери напора
Энергетика Уравнение может быть выражено в терминах напора и потери напора путем деления каждого члена на удельный вес жидкости. Общий напор в потоке жидкости в трубе или воздуховоде может быть выражен как сумма напора по высоте, скоростного напора и напора.
Примечание ! Напоры в приведенных ниже уравнениях основаны на самой жидкости в качестве эталонной жидкости. Подробнее о голове читайте здесь.
p 1 / γ + v 1 2 / 2 g + h 1 = p 2 / γ + v 2 2 / 2 г + ч 2 (6)
0003
Δ ч потеря = потеря напора (м “жидкость”, футы “жидкость”)
γ = ρ g = удельный вес жидкости (Н/м 3 , фунт/фут 3 )
Для горизонтального стационарного потока v 1 = v 2 и p 1 = p 900 08 2 , – (4) можно преобразовать в:
ч убыток = ч 1 – h 2 (6a)
где
Δ h = p/γ = напор (м “жидкость”, фут “жидкость”)
Большая потеря напора на трение в трубе или воздуховоде из-за трения может быть выражена как: (л/д ч ) (в 2 / 2 г) (7)
где
Δ ч потеря = потеря напора (м, фут)
Незначительная или динамическая потеря напора зависит от скорости потока, плотности и коэффициент для фактической составляющей.
Δ p незначительные_потери = ξ v 2 / (2 г) (8)
Коэффициент трения –
λКоэффициент трения зависит от течения –
- ламинарного,
- переходного или
- турбулентного
и шероховатости трубы или воздуховода.
Чтобы определить коэффициент трения, мы сначала должны определить, является ли поток ламинарным, переходным или турбулентным, а затем использовать соответствующую формулу или диаграмму.
Коэффициент трения для ламинарного потока
Для полностью развитого ламинарного потока шероховатостью воздуховода или трубы можно пренебречь. Коэффициент трения зависит только от числа Рейнольдса – Re – и может быть выражено как:
λ= 64 / Re 007, где
Re = безразмерное число Рейнольдса
Расход равен
- ламинарный при Re < 2300
- переходный при 2300 < Re < 4000
- турбулентный при Re > 4000
Коэффициент трения для Переходный поток
Если течение нестационарное – 2300 < Re < 4000 - течение колеблется между ламинарным и турбулентным течением, и коэффициент трения определить невозможно.
Коэффициент трения для турбулентного потока
Для турбулентного потока коэффициент трения зависит от числа Рейнольдса и шероховатости стенки воздуховода или трубы. В функциональной форме это можно выразить как:
λ = f( Re, k/d h ) (10)
где
k = абсолютная шероховатость стенки трубы или воздуховода (мм, фут)
k/d 900 08 ч = относительная шероховатость – или коэффициент шероховатости
Шероховатость материалов определяется опытным путем. Абсолютная шероховатость для некоторых распространенных материалов указана в таблице ниже
| Поверхность | Абсолютная шероховатость – k | |
|---|---|---|
| (10 -3 м) | (футы) | Медь, свинец, латунь, алюминий (новый) | 0,001–0,002 | 3,3–6,7 10 -6 |
| Трубы из ПВХ и пластика | 0,0015 – 0,007 | 0,5 – 2,33 10 -5 | 9073 5
| Эпоксидная, винилэфирная и изофталевая труба | 0,005 | 1,7 10 -5 |
| Нержавеющая сталь, дробеструйная обработка | 0,001 – 0,006 | (0,00328 – 0,0197) 10 -3 | Нержавеющая сталь, точеная | 0,0004 – 0,006 | (0,00131 – 0,0197) 10 – 3 |
| Нержавеющая сталь, электрополированная | 0,0001 – 0,0008 | (0,000328 – 0,00262) 10 -3 | 90 735
| Труба стальная промышленная | 0,045 – 0,09 | 1,5 – 3 10 -4 |
| Сталь тянутая | 0,015 | 5 10 -5 | Сварная сталь | 0,045 | 1,5 10 -4 |
| Оцинкованная сталь | 0,15 | 5 10 -4 |
| Ржавая сталь (коррозия) | 0,15 – 4 | 5 – 133 10 -4 |
| Новый чугун | 0,25 – 0,8 | 8 – 27 10 -4 |
| Изношенный чугун | 0,8 – 1,5 | 2,7 – 5 10 -3 90 752 |
| Ржавый чугун | 1,5 – 2,5 | 5 – 8,3 10 -3 |
| Чугун листовой или асфальтированный | 0,01 – 0,015 | 3,33 – 5 10 -5 | Сглаженный цемент | 0,3 | 1 10 -3 |
| Рядовой бетон | 0,3 – 1 | 1 – 3,33 10 -3 |
| Грубый бетон | 0,3 – 5 | 907 51 1 – 16,7 10 -3|
| Хорошо строганная древесина | 0,18 – 0,9 | 6 – 30 10 -4 |
| Обычное дерево | 5 | 16,7 10 -3 |
Коэффициент трения – λ – можно рассчитать по Уравнение Коулбрука :
1 / λ 1/2 = -2,0 log 10 [ (2,51 / (Re λ 1/2 )) + (k / d ч ) / 3,72 ] (11)
Поскольку коэффициент трения – λ – находится в обеих частях уравнения, его необходимо решать путем итерации.
Зная число Рейнольдса и шероховатость, можно рассчитать коэффициент трения λ в конкретном потоке.
Графическим представлением уравнения Коулбрука является диаграмма Муди :
- Диаграмма Муди – диаграмма Муди в формате для печати.
С помощью диаграммы Муди мы можем найти коэффициент трения, если мы знаем число Рейнольдса – Re – и
относительный коэффициент шероховатости – 90 007 к/д ч
На диаграмме видно, как коэффициент трения зависит от числа Рейнольдса для ламинарного течения, как коэффициент трения не определен для переходного течения, и как коэффициент трения зависит от коэффициента шероховатости для турбулентного течения.
Для гидравлических гладких труб коэффициент шероховатости ограничивается нулем, а коэффициент трения более или менее зависит только от числа Рейнольдса.
Для полностью развитого турбулентного потока коэффициент трения зависит только от коэффициента шероховатости.
Пример – Потеря давления в воздуховодах
Воздух на 0 o C течет в 10 м оцинкованный воздуховод – 315 мм диаметр – со скоростью 15 м/с .
Можно рассчитать число Рейнольдса: 9(12)
где 9001 4
Re = число Рейнольдса
v = скорость (м/с)
ρ = плотность воздуха (кг/м 3 )
μ = динамическая или абсолютная вязкость ( 900 07 Нс/м 2 )
Расчетное число Рейнольдса:
Re = (15 м/с) (315 мм) (10 -3 м/мм ) (1,23 кг/м 3 ) / (1,79 10 -5 Ns / м 2 )
= 324679 (кгм/с 2 )/Н
= 324679 ~ Турбулентный поток 9001 4
Турбулентный поток указывает на необходимость использования уравнения Коулбрука (9) для определения коэффициент трения – λ -.
С шероховатостью – ε – для оцинкованной стали 0,15 мм коэффициент шероховатости можно рассчитать:
= (0,15 мм) / (315 мм)
= 4,76 10 -4
Используя графическое представление уравнения Коулбрука – диаграмму Муди – коэффициент трения – λ – можно определить по формуле:
λ = 0,017
Основные потери для воздуховода 10 м можно рассчитать с помощью уравнения Дарси-Вейсбаха (3) или (6):
Δp потери = λ ( l / d h ) ( ρ v 2 / 2 )
= 0,017 ((10 м) / (0,315 м)) ( (1,23 кг/м 9 0117 3 ) (15 м/с) 2 / 2 )
= 74 Па (Н/м 2 )
Местные потери давления, соответствующие клапанам и фитингам в гидравлических сетях выражаются следующим соотношением:
= динамическое давление жидкости. Местные потери давления подразделяются на 2 категории:
Следует отметить, что все следующие значения установлены по наименьшему диаметру. Это значение может быть преобразовано для наибольшего диаметра следующим образом: (d большой /d маленький ) 4 .
Этот расчет должен выполняться отдельно для каждого размера трубы,
используя соответствующую скорость в этом сечении трубы. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
