Расчет площади воздуховодов – Мир Климата и Холода
Расчет площади воздуховодов выполняется при подготовке спецификации, а также на производстве для понимания, сколько сырья потребуется для изготовления проектного количества воздуховодов.
Эта задача может звучать следующим образом:
- расчет площади воздуховодов
- узнать площадь воздуховода
- расчет м2 воздуховодов
Расчет площади воздуховодов онлайн
Курс МП1 — расчет воздуховодов и воздухообмена
Расчет выполняется отдельно для круглых и прямоугольных воздуховодов. Исходными данными являются:
- Длина воздуховода
- Диаметр круглого или стороны сечения прямоугольного воздуховода.
Представленный выше калькулятор позволяет быстро рассчитать площадь любого воздуховода онлайн. Вычисления производятся на основе введенных значений и не предусматривают запаса. Чтобы не ошибиться при изготовлении воздуховодов, рекомендуем полученную площадь увеличить на 10-20%.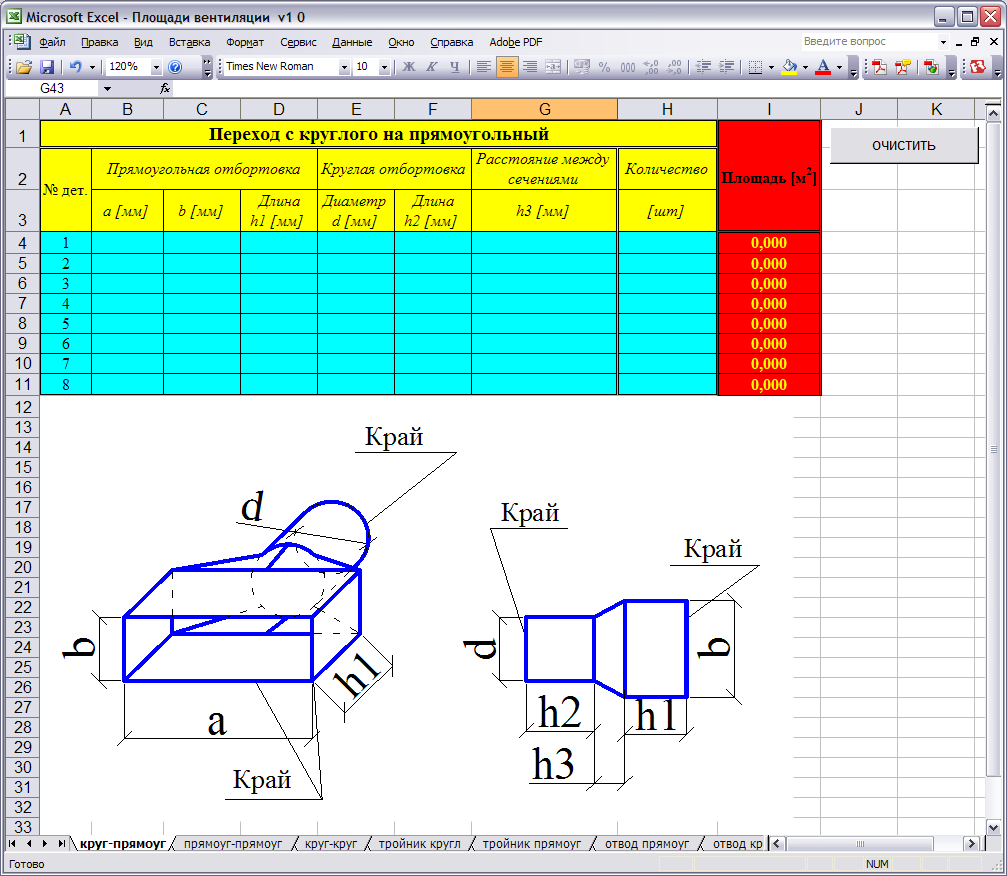
Формула расчёта площади воздуховодов
Площадь воздуховодов определяется путём перемножения периметра сечения воздуховода на длину воздуховода:
- S = П·L, где П и L — соответственно, периметр и длина воздуховода в метрах.
Важно помнить о размерности величин в формуле, приведённой выше. Обычно сечение воздуховода задаётся в миллиметрах (например, диаметр 250 или сечение 500×250), а длина — в метрах (например, 5 метров). Но в формулу необходимо подставлять все величины, выраженные в метрах. Причем, предварительно следует вычислить длину периметра сечения воздуховода.
Для упрощения задачи по расчету площади воздуховодов применяют готовые формулы для круглых и прямоугольных воздуховодов.
Расчет площади круглого воздуховода
Расчет площади круглого воздуховода выполняется по формуле:
- S = π·D·L, где D и L — диаметр и длина воздуховода в метрах.
Например, воздуховод диаметром 250 мм и длиной 5 метров будет иметь следующую площадь:
- S = π·(250/1000)·5 ≈ 4 м2 — это и есть м2 воздуховода (метраж/квадратура).
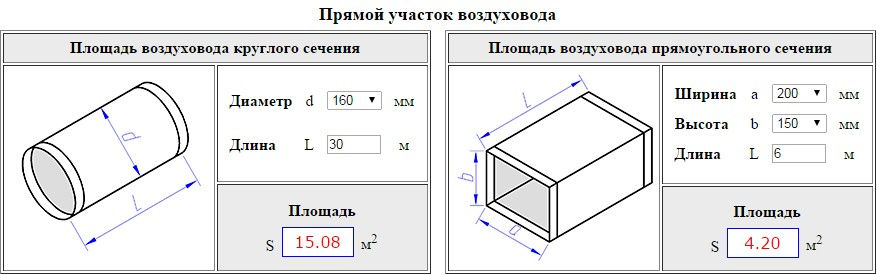
Расчет площади прямоугольного воздуховода
Расчет площади прямоугольного воздуховода выполняется по формуле:
- S = 2·(A+B)·L, где A и B — длины сторон воздуховода (в метрах), а L — длина воздуховода в метрах.
Например, воздуховод диаметром сечением 500×300 (то есть со сторонами 0,5м и 0,3м) и длиной 10 метров будет иметь следующую площадь:
- S = 2·(0,5+0,3)·10 = 16 м2.
Расчет площади воздуховодов различной формы и фасонных изделий
Содержание статьи
Производительность системы вентиляции напрямую зависит от правильности ее проектирования. Важнейшую роль в этом играет верный расчет площади воздуховодов. От него зависит:
- Беспрепятственное движение воздушного потока в нужных объемах, его скорость;
- Герметичность системы;
- Уровень шума;
- Расход электроэнергии.

Воздуховод
Для того чтобы узнать все нужные значения, можно обратиться в соответствующую компанию или же воспользоваться специальными программами (их можно легко отыскать в интернете). Однако, при необходимости, найти все необходимые параметры возможно и самостоятельно. Для этого существуют формулы.
Использование их довольно просто. Вам также достаточно вписать параметры вместо соответствующих букв и найти результат. Формулы помогут вам отыскать точные значения, с учетом всех индивидуальных факторов. Обычно они применяются при инженерных работах по проектированию системы вентиляции.
Вернуться к содержанию ↑Как найти верные значения
Для того чтобы произвести расчет площади сечения нам потребуется информация:
- О минимально необходимом воздушном потоке;
- О предельно возможной скорости воздушного потока.
Для чего нужен правильный расчет площади:
- Если скорость потока будет выше положенного предела, то это станет причиной падения давления.
 Эти факторы, в свою очередь, повысят расход электроэнергии;
Эти факторы, в свою очередь, повысят расход электроэнергии; - Аэродинамический шум и вибрации, если все выполнено верно, будут в пределах нормы;
- Обеспечение нужного уровня герметичности.
Воздуховод в разборе
Это также позволит повысить эффективность системы, поможет сделать ее долговечной и практичной. Нахождение оптимальных параметров сети – принципиально важный момент в проектировании. Только в этом случае система вентиляции прослужит долго, отлично справляясь со всеми своими функциями. Особенно это актуально для больших помещений общественного и производственного значения.
Чем большим будет сечение, тем ниже будет скорость воздушного потока. Это также уменьшит аэродинамический шум и расход электроэнергии. Но есть и минусы: стоимость таких воздуховодов будет выше, и конструкции не всегда можно установить в пространство над навесным потолком. Однако это возможно с прямоугольными изделиями, высота которых меньше. В то же время изделия круглой формы проще устанавливаются и обладают важными эксплуатационными преимуществами.
Что именно выбрать, зависит от ваших требований, приоритета экономии электроэнергии, самих особенностей помещения. Если вы желаете сэкономить электроэнергию, сделать шум минимальным и у вас есть возможность установить крупную сеть, выбирайте систему прямоугольной формы. Если же приоритетом является простота установки или в помещении сложно установить конструкции прямоугольного типа, вы можете выбрать изделия круглого сечения.
Расчет площади выполняется по следующей формуле:
Sc = L * 2, 778/V
Sc здесь – площадь сечения;
L – расход воздушного потока в метрах в кубе/час;
V – скорость воздушного потока в воздуховоде в метрах в секунду;
2,778 – необходимый коэффициент.
Трубы для воздуховода
После того, как расчет площади выполнен, вы получите результат в квадратных сантиметрах.
Фактическую площадь воздуховодов помогут определить следующие формулы:
Для круглых: S = Пи * D в квадрате /400
Для прямоугольных: S = A * B /100
S здесь – фактическая площадь сечения;
D – диаметр конструкции;
A и B – высота и ширина конструкций.
Как определить потери давления
Расчет сопротивления сети позволяет принять во внимание потери давления. Поток воздуха, во время движения, испытывает определенное сопротивление. Для его преодоления важно соответствующее давление. Давление это измеряется в Па.
Для того чтобы узнать нужный параметр, потребуется следующая формула:
P = R * L + Ei * V2 * Y/2
R здесь – удельные сокращения давления на трение в сети;
L – протяженность воздуховодов;
Ei – коэффициент местных потерь в сети в сумме;
V – скорость воздуха на рассматриваемом участке сети;
Y – плотность воздуха.
R можно узнать в соответствующем справочнике. Ei зависит от местного сопротивления.
Как узнать оптимальную мощность нагревателя воздуха
Для того чтобы узнать оптимальную мощность нагревателя воздуха, требуются показатели нужной температуры воздуха и самой минимальной температуры снаружи помещения.
Составные элементы воздуховода
Минимальная температура в системе вентиляции – 18 градусов. Температура снаружи помещения зависит от климатических условий. Для квартир оптимальная мощность нагревателя обычно составляет от 1 до 5 кВт, для офисных помещений – 5-50 кВт.
Температура снаружи помещения зависит от климатических условий. Для квартир оптимальная мощность нагревателя обычно составляет от 1 до 5 кВт, для офисных помещений – 5-50 кВт.
Точный расчет мощности нагревателя в сети позволит выполнить следующая формула:
P = T * L * Cv /1000
P здесь – мощность нагревателя в кВт;
T – разность температуры воздуха внутри и снаружи помещения. Это значение можно найти в СНиП;
L – производительность системы вентиляции;
Cv – теплоемкость, равная 0,336 Вт*ч/метры квадратные/градус по Цельсию.
Дополнительная информация
Для того чтобы узнать нужные параметры фасонных изделий и самой конструкции, не обязательно самостоятельно выполнять расчет частей сети вентиляции. Для нахождения всех значений существуют специальные программы. Вам достаточно ввести требуемые числа, и вы получите результат за доли секунды.
Рассчитываются значения креплений, фасонных частей, воздуховодов обычно инженерами, занимающимися проектированием систем вентиляции. Но и они применяют таблицы, в которых имеются все требуемые коэффициенты, формулы, значения.
Но и они применяют таблицы, в которых имеются все требуемые коэффициенты, формулы, значения.
Также существует специальная таблица эквивалентных диаметров воздуховодов. Это таблица диаметров воздуходувов круглой формы, в которых снижение давления на трение равна снижению давления в конструкциях прямоугольной формы. Эквивалентный диаметр конструкции воздуходува требуется тогда, когда необходимо произвести расчет прямоугольных воздуходувов, и при этом применяется таблица для изделий круглой формы.
Стальные трубы для воздуховода
Известно три способа узнать эквивалентное значение:
- Ориентируясь на скорость;
- По поперечному сечению;
- По расходу.
Все эти значения связаны с шириной и другими значениями воздуховодов. Для каждого из параметров применяется своя методика пользования таблицами. Итоговый результат – значение потери давления на трение. Вне зависимости от того, какую методику вы применили, результат получается одинаковым.
В интернете вы легко сможете найти таблицы, программы, справочники, необходимые для подсчета площади и иных параметров самих конструкций, креплений. Самое простое – воспользоваться специальными программами. В этом случае от вас требуется только ввод нужных значений. При этом результаты вы получите довольно точные.
Самое простое – воспользоваться специальными программами. В этом случае от вас требуется только ввод нужных значений. При этом результаты вы получите довольно точные.
Пример создания воздуховодов
| Автор | Поделитесь | Оцените | Виктор Самолин |
|---|
Как посчитать площадь воздуховода прямоугольного сечения, формула
Перед созданием вентиляционной системы особое значение уделяется правильной планировке и расчету всех необходимых параметров. Наиболее важным из таких параметров считается площадь будущего воздуховода. Чтобы выполнить подобную задачу квалифицированные мастера учитывают такие параметры, как:
- — объемы воздуха;
- — скорость воздушных масс;
- — потери давления.
Количество материалов
Выполняются подобные расчеты с целью определения количества требуемых материалов. Это зависит от:
Это зависит от:
- — габаритов канала;
- — количества комнат;
- — конструктивных особенностей будущей вентиляционной системы.
Измеряя величину сечения, необходимо учесть особо важную деталь. Чем больше такая величина, тем более медленно будут двигаться по трубам воздушные массы. Многие неопытные домовладельцы не знают, как посчитать площадь воздуховода прямоугольного сечения. Профессиональные мастера используют для подобной задачи специальную формулу. Системы с высокими показателями сечения отличаются низким показателем аэродинамического шума. Следовательно, принудительная вентиляция в подобных системах потребует меньших расходов на электроэнергию.
Каждая проектируемая вентиляционная система имеет особые:
- — базовые габариты;
- — конфигурацию;
- — дополнительные элементы;
- — конструкцию.
Перечисленные критерии необходимо учесть при подсчете суммарной площади требуемого материала, с использованием которого будет создаваться воздуховод. Прямоугольные конструкции вентиляционных систем требуют определения:
Прямоугольные конструкции вентиляционных систем требуют определения:
- — суммарной длины;
- — высоты;
- — ширины.
Полученные показатели позволяют специалистам выбрать оптимальное количество материалов. Общие подсчеты также предполагают учет:
- — полуотводов;
- — отводов.
Перечисленные детали могут иметь различную конфигурацию. Если круглые элементы требуют знания диаметра будущего воздуховода, то для вычисления площади прямоугольных систем, необходим учет:
- — высоты отвода;
- — угла поворота;
- — ширины изделия.
Любой подобный расчет предполагает использование специалистом конкретной формулы. Для обустройства качественной вентиляционной системы опытные мастера чаще всего выбирают оцинкованные фасонные элементы и воздуховоды, обладающие продленным ресурсом. Расчет площади считается наиболее важным параметром при сооружении прямоугольной вентиляции. Полученные показатели позволяют профессионалам создавать оптимальные системы, которые прослужат многие годы.
Сравнение круглых и прямоугольных воздуховодов
В этой статье мы расскажем о преимуществах и недостатках использования воздуховодов круглого и прямоугольного сечения.
Неотъемлемой частью вентиляционных систем является магистраль, по ней и доставляется воздух из пункта «А» в пункт «Б». Она состоит из воздуховодов, которые бывают двух видов – круглые и прямоугольные. Давайте разберемся, какие воздуховоды подойдут для решения Вашей задачи.
Круглые воздуховоды
Основным преимуществом воздуховодов круглого сечения является герметичность. Спирально-навивные воздуховоды имеют плотные швы, которые дают им дополнительную жесткость, а за счет того, что при соединении воздуховодов используется ниппель. Все фасонные изделия также имеют зауженное сечение — минимизируются потери транспортируемого воздуха.
«Живое » сечение круглого воздуховода охватывает весь его периметр, что совместно с плавными поворотами фасонных изделий позволяет использовать его аэродинамические свойства с максимальным КПД, и минимальной потерей давления.
Не менее важным преимуществом является цена. Круглые воздуховоды значительно дешевле прямоугольных, потому что периметр прямоугольного воздуховода больше чем длина окружности круглого с такой же площадью сечения , соответственно на изготовление и дальнейшую изоляцию используется меньше материалов. Производство круглых воздуховодов на данный момент полностью автоматизировано. Это тоже позволяет снизить издержки при их изготовлении.
Собирать системы из таких воздуховодов тоже значительно проще – ниппель вставляется в воздуховод, скручивается саморезами в нескольких местах и проклеивается алюминиевым скотчем.
Основной недостаток круглых воздуховодов — это габариты. В помещениях с низкими потолками, узких шахтах и т.п. выгоднее использовать прямоугольные воздуховоды. По ГОСТ 24751-81 допустимое соотношение сторон прямоугольных воздуховодов 6,3.
С некоторыми неудобствами можно столкнуться при монтаже воздуховодов круглого сечения. Смонтировать врезку по месту, или изготовить недостающее фасонное изделие сможет только опытный монтажник, и для этого понадобится специальное оборудование.
Прямоугольные воздуховоды
Что касается воздуховодов прямоугольного сечения, то пожалуй, их единственным преимуществом является возможность маневрирования соотношением сторон, чтобы вместить систему в ограниченное пространство.
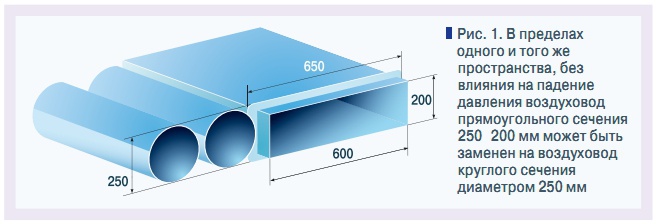
Эквивалентный диаметр — диаметр круглого воздуховода, в котором потеря давления на трение при одинаковой длине равна его потере в прямоугольном воздуховоде.
i Эквивалентный диаметр прямоугольного воздуховода можно вычислить по формуле:
 25) (1), где
25) (1), гдеde = эквивалентный диаметр (мм)
a = длина стороны A (мм)
b = длина стороны B (мм)
Это означает что площадь сечения прямоугольного воздуховода будет больше площади сечения круглого воздуховода с эквивалентным диаметром
Если S1 = S2, то A+A+B+B (периметр) > 2*π*R (длина окружности)
Надеемся, что наша статья будет полезной для Вас при подборе воздуховодов!
Автор статьи: Сергей Шаповалов
Заместитель генерального директора
по производству ООО “ЦВС”.
Методика. Площадь воздуховодов MagiCAD. Andrey Shirshov, PDF Free Download
Все прототипы В года
1. Прототип задания B9 ( 245359) Все прототипы В5 2013 года Найдите квадрат расстояния между вершинами и прямоугольного параллелепипеда, для которого,,. 2. Прототип задания B9 ( 245360) Найдите расстояние
Прототип задания B9 ( 245359) Все прототипы В5 2013 года Найдите квадрат расстояния между вершинами и прямоугольного параллелепипеда, для которого,,. 2. Прототип задания B9 ( 245360) Найдите расстояние
ИВЕНТ ПРАЙС-ЛИСТ 2018
ИВЕНТ ПРАЙС-ЛИСТ 2018 ОГЛАВЛЕНИЕ ВОЗДУХОВОД КРУГЛОГО СЕЧЕНИЯ СПИРАЛЬНОНАВИВНОЙ ИЗ ОЦИНКОВАННОЙ СТАЛИ… 2 ВОЗДУХОВОД КРУГЛОГО СЕЧЕНИЯ ПРЯМОШОВНЫЙ ИЗ ОЦИНКОВАННОЙ СТАЛИ… 3 ОТВОДЫ КРУГЛОГО СЕЧЕНИЯ ИЗ ОЦИНКОВАННОЙ
ПодробнееВоздуховоды Общие сведения
Воздуховоды Общие сведения Воздуховоды (прямые и фасонные части) прямоугольного и круглого сечения изготавливаются по видам и размерному ряду принятому в : – ВСН 353 86 «Проектирование и применение воздуховодов
Все прототипы задания В9 (2013)
Все прототипы задания В9 (2013) ( 245359) Найдите квадрат расстояния между вершинами и прямоугольного параллелепипеда, для которого,,. ( 245360) Найдите расстояние между вершинами и прямоугольного параллелепипеда,
( 245360) Найдите расстояние между вершинами и прямоугольного параллелепипеда,
Воздуховоды круглого сечения
Воздуховоды Воздуховоды (прямые и фасонные части) прямоугольного и круглого сечения изготавливаются по видам и размерному ряду принятому в : – ВСН 353-86 «Проектирование и применение воздуховодов из унифицированных
Подробнее7. Задачи по стереометрии
РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ 7 Задачи по стереометрии методические указания для абитуриентов физического факультета Ростов-на-Дону 00 Печатается по решению учебнофакультета РГУ методической комиссии
ПодробнееВоздуховод круглый -2- Без фланцев. На фланцах. «Бабочка» Площадь живого сечения, Площадь поверхности 1 п.м., Вес 1 п.м. Толщина стали s, Цена,
Воздуховод круглый Диаметр Толщина стали s, Площадь поверхности 1 п.м., Площадь живого сечения, Вес 1 п.м. d, мм мм м 2 м 2 кг / м.п. 100 0,5 0,32 0,008 1,2 156 125 0,5 0,4 0,012 1,4 195 160 0,5 0,51 0,02
ПодробнееRunicom tel.:+7(495) Page 1 of 20
ВОЗДУХОВОДЫ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ ИЗ ОЦИНКОВАННОЙ СТАЛИ Толщина металла, Прямой участок длиной L = 1250 Длина прямого участка, Прямой участок длиной свыше 1250 в руб/м 2 Прямой участок длиной менее 1250
Подробнее3 ОСНОВНЫЕ ФОРМУЛЫ ДЛЯ СПРАВОК
Глава ОСНОВНЫЕ ФОРМУЛЫ ДЛЯ СПРАВОК.. Геометрия Треугольники. Два треугольника равны, если =, b = b, γ = γ ; c = c, α = α, β = β ; =, b = b, c = c.. Два треугольника подобны, если α = α, β = β ; b =, b
ПодробнееТригонометрические уравнения
Тригонометрические уравнения С б) Укажите корни, принадлежащие отрезку. а) Решите уравнение б) Укажите корни уравнения, принадлежащие отрезку а) Решbте уравнение. б) Укажите корни этого уравнения, принадлежащие
ПодробнееПрямоугольный параллелепипед
ЗАДАНИЕ 10 Стереометрия Куб 1.Площадь поверхности куба равна 18. Найдите его диагональ. 2. Диагональ грани куба равна 2 6. Найдите диагональ куба. 3. Диагональ грани куба равна 6. Найдите диагональ куба.
ПодробнееПРЯМОЙ И НАКЛОННЫЙ КОНУС
ПРЯМОЙ ЦИЛИНДР Пусть в пространстве заданы две параллельные плоскости и. F круг в одной из этих плоскостей, например. Рассмотрим ортогональное проектирование на плоскость. Проекцией круга F будет круг
ПодробнееМногогранники. Призма
Справка В9 Многогранники Многогранник это такое тело, поверхность которого состоит из конечного числа плоских многоугольников. Призма Призмой называется многогранник, который состоит из двух плоских многоугольников,
ПодробнееЗадачи по с т е р е о м е т р и и
Задачи по с т е р е о м е т р и и Ермак Елена Анатольевна, доктор педагогических наук, профессор кафедры математического анализа и методики обучения математике Псковского государственного университета
ПодробнееСХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ
СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ 1. Найти область определения функции.. Исследовать четность и периодичность функции. 3. Исследовать точки разрыва, найти вертикальные асимптоты. 4. Найти наклонные асимптоты
ПодробнееПрайс-лист на ВЕНТИЛЯЦИЮ
Прайс-лист на ВЕНТИЛЯЦИЮ Содержание 1. Прямые участки 2. 3. Сэндвич нержавеющая сталь 4. Отвод 5. Переход 6. Тройник 7. Врезка, Заглушка, Нипель 8. Гибкая вставка, Дефлектор, Обратный клапан 9. Дросель-клапан,
ПодробнееВсе прототипы заданий В года
1. Прототип задания B13 ( 27054) выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины. Все прототипы заданий В13
ПодробнееЗадание 8, 14. Стереометрия
Задание 8, 4. Стереометрия Основные определения Аксиомы стереометрии Теорема. Через любые три точки, не лежащих на одной прямой, проходит плоскость, и притом только одна. Теорема. Если две точки прямой
ПодробнееВсе прототипы заданий года
1. Прототип задания 12 ( 27064) Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы. Все прототипы заданий 12
ПодробнееСОДЕРЖАНИЕ:
1 СОДЕРЖАНИЕ: ВОЗДУХОВОДЫ…….. 2 – Воздуховоды и фасонные детали круглого сечения…….. 3 – Зонты круглые……. 11 – Дефлектора круглые…. 12 – Насадки с водоотводящим кольцом…….. 13 – Вставки
ПодробнееКалендарно – тематический план
Календарно – тематический план ГЕОМЕТРИЯ Класс 11 Годовое количество часов 68 Количество часов в неделю – 2 Учебный год – 2013 2014 Учитель Беликова Галина Ивановна МКОУ «Борятинская СОШ» Согласовано зам.
ПодробнееВоздуховоды прямоугольного сечения
Воздуховоды прямоугольного сечения Из оцинкованной стали Цена в руб/м 2 Толщина металла, мм Прямой участок 0,55 без фланцев 306 0,55 на фланцах (шина No20) 379 0,7 без фланцев 336 0,7 на фланцах (шина
ПодробнееПрайс-лист на ВЕНТИЛЯЦИЮ
Прайс-лист на ВЕНТИЛЯЦИЮ Содержание 1. Прямые участки 2. 3. Сэндвич нержавеющая сталь 4. Отвод 5. Переход 6. Тройник 7. Врезка, Заглушка, Нипель 8. Гибкая вставка, Дефлектор, Обратный клапан 9. Дросель-клапан,
ПодробнееТест 250. Отрезок. Длина
Тест 250. Отрезок. Длина Длина отрезка равна 1, если он является: 1. высотой равностороннего треугольника со стороной 2; 2. третьей стороной треугольника, в котором две другие стороны равны 1 и 2, а угол
ПодробнееВоздуховоды и фасонные изделия
28.12.2018 Воздуховоды и фасонные изделия ООО «СПН-Полимер» Воздуховоды круглого и прямоугольного сечения из полипропилена (ПП-С, ПП-Г) полиэтилена (ПНД) поливинилхлорида (ПВХ) Компания ООО «СПН – Полимер»
ПодробнееВсе прототипы заданий В года
1. Прототип задания B13 ( 27064) Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы. Все прототипы заданий
ПодробнееВоздуховоды и фасонные изделия
Воздуховоды и фасонные изделия Оцинкованные прямоугольные воздуховоды на фланце из шинорейки Прямоугольные воздуховоды из углеродистой стали Толщина стали,мм /Шина Размер изделия / Цена A,B 150, L>1250
ПодробнееВсе прототипы задания В11 (2013)
Все прототипы задания В11 (2013) ( 25541) Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). ( 25561) Найдите площадь поверхности многогранника, изображенного
ПодробнееТехнический комментарий
СОДЕРЖАНИЕ Технический комментарий Ниппельное соединение воздуховодов Заказ воздуховодов Прямой участок Отвод 900 Отвод 600 Отвод 450 Отвод 300 Отвод 150 Переходы Тройник Ниппель Муфта Врезка круглая Заглушка
ПодробнееПрограммы испытаний по математике
Программы испытаний по математике 1. Основные математические понятия и факты Арифметика, алгебра и начала анализа Натуральные числа (N). Простые и составные числа. Делитель, кратное. Наибольший общий делитель,
ПодробнееТест по теме «Задачи стереометрии»
Тест по теме «Задачи стереометрии» Тест составлен на основе учебника «Геометрия, 10-11 класс (базового и профильного уровней ) / Л.С. Атанасян и др. – М.: «Просвещение», 2010. Аннотация: Задачи теста соответствуют
ПодробнееОсновные определения, теоремы и формулы планиметрии.
Основные определения, теоремы и формулы планиметрии. Обозначения: AВС треугольник с вершинами А, B, С. а = BC, b = AС, с = АB его стороны, соответственно, медиана, биссектриса, высота, проведенные к стороне
ПодробнееСтереометрия: комбинации тел.
А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Стереометрия: комбинации тел. 27041. Прямоугольный параллелепипед
ПодробнееВрезка круглая в воздуховод.
Врезки круглого сечения изготавливаются из оцинкованной или нержавеющей стали.
Возможны любые размеры (d, L) с учетом технологических ограничений.
Врезка в прямоугольный воздуховод (В прям.)
Узнать стоимость и размеры прямой врезки, Вы можете в программе VentZakaz, в разделе: Врезки -> Круг. прямая.
Врезка в круглый воздуховод (В круг.)
Узнать стоимость и размеры врезки в круглый воздуховод, Вы можете в программе VentZakaz, в разделе: Врезки -> Круг. в диаметр.
Примечание:
Площадь в таблице для врезки в круглый воздуховод, рассчитана с учетом того, что ее диаметр равен диаметру воздуховода.
При разных диаметрах площадь может не совпадать со значениями в таблице.
Таблица стандартных размеров врезок.
| d, мм | В прям. | В круг. | L, мм | S, м2 | L, мм | S, м2 |
|---|---|---|---|---|
| 100 | 100 | 0,038 | 80 | 0,046 |
| 125 | 100 | 0,047 | 80 | 0,059 |
| 160 | 100 | 0,060 | 90 | 0,080 |
| 200 | 100 | 0,075 | 90 | 0,107 |
| 250 | 100 | 0,094 | 90 | 0,143 |
| 315 | 100 | 0,119 | 100 | 0,197 |
| 355 | 100 | 0,134 | 100 | 0,233 |
| 400 | 100 | 0,151 | 110 | 0,276 |
| 450 | 100 | 0,170 | 110 | 0,329 |
| 500 | 100 | 0,188 | 110 | 0,385 |
| 560 | 100 | 0,211 | 120 | 0,457 |
| 630 | 100 | 0,237 | 120 | 0,549 |
| 710 | 120 | 0,268 | 120 | 0,663 |
| 800 | 120 | 0,301 | 120 | 0,804 |
| 900 | 120 | 0,339 | 130 | 0,975 |
| 1000 | 120 | 0,377 | 130 | 1,162 |
| 1250 | 120 | 0,471 | 130 | 1,698 |
Выполняем токарные работы любой сложности. Подробнее.
формулы для обычной, круглой, треугольной комнаты
Перед продажей квартиры нам необходимо определить ее характеристики: узнать квадратуру комнат, записать высоту потолков, оценить другие параметры. Высчитать площадь комнаты в квадратных метрах будет полезно и при покупке новостройки: станет проще оценивать представленное на рынке жилье, т. к. вы сможете сравнить его со своим. Но как это сделать? Рассказывают наши эксперты.
Интересно, что метр квадратный официально обозначается как м² или как m² (международная система написания единиц измерения). Записывать его как м2 — ошибка. Если вы не можете поставить надстрочный знак, используйте сокращение «кв. м».
Формулы для расчета квадратуры комнаты
В зависимости от особенностей помещения рекомендации о том, как сосчитать площадь комнаты в квадратных метрах, будут различаться. Мы представили ниже подборку формул, которые используются для определения квадратуры помещения.
Базовая формула
Если вы разбираетесь, как посчитать площадь комнаты в квадратных метрах, и помещение у вас квадратное или прямоугольное, вам повезло. Необходимые арифметические вычисления будут совсем несложными. Площадь комнаты в квадратных метрах можно получить, перемножив ее длину и ширину. Это значит, что если у вас длина комнаты 10 метров, а ширина — 9, то расчет будет следующим:
100 х 90 = 90
Однако, измеряя комнату, мы обычно получаем значение в сантиметрах, а не в метрах, например, длина будет 1112 см, а ширина — 961. Для корректного ответа нужно перевести в метры или изначальные величины, или уже готовый результат.
1. Переводим в метры изначальные величины
Так как в 1 метре 100 сантиметров, нужно поделить сантиметры на 100, чтобы получить метры.
1112 / 100 = 11,12 м
961 / 100 = 9,61 м
11,12 х 9,61 = 106,9 м²
2. Переводим в метры результат
Так как в 1 квадратном метре 10000 квадратных сантиметров, конечный результат нужно поделить на 10000.
1112 х 961 = 1068632 см²
1068632 / 10000 = 106,9 м²
Обратите внимание! В обоих случаях результат получался с большим количеством знаков после запятой (106,8632 и т. д.). Мы округлили его по правилам округления, согласно которому цифра, записанная в выбранном разряде (у нас это десятые), не меняется, если за ней следует 0, 1, 2, 3 или 4 и увеличивается на один, если за ней следует 5,6,7,8 или 9. У нас за десятыми следует 6 сотых, поэтому мы увеличиваем цифру на 1, получая 106,9 вместо 106,8.
Расчет площади круглой комнаты
Не всегда удается выделить на плане исключительно прямоугольники. Сегодня все чаще строится жилье нестандартной конфигурации — с полукруглыми нишами и другими овальными элементами. Если у вас обнаружился элемент в виде круга, используйте формулу:
S комнаты = πR², где R – радиус. Число «Пи» в этом случае берется как 3,14.
Не забудьте, что круглая ниша у вас обрезана, поэтому результат нужно поделить на два, если у вас полукруг и т. д.
Арки считаются по двум формулам: круга и квадрата. Сначала на плане разделяете арку на полукруг и прямоугольный сегмент, потом рассчитываете обе площади и складываете их между собой.
Площадь треугольника
Как рассчитать площадь комнаты в м², если она треугольная? Для таких случаев используется формула Герона. Она выглядит так:
Площадь комнаты = √ (P(P – A) х (Р – В) х (Р – С))
В А, В и С в данном расчете — это длины сторон треугольника, площадь которого нужно определить. А Р является его полупериметром. Его нужно рассчитать заранее, сложив длину всех сторон и поделив ее на два. Формула выглядит так: Р = (А + В + С) / 2.
Как проходит расчет
Даже зная, как найти площадь комнаты в квадратных метрах, многие сомневаются, с чего начать в собственной квартире. В первую очередь вооружитесь калькулятором, рулеткой, карандашом и листом бумаги. Вам потребуется составить план помещения. Этот пункт можно пропустить, если у вас есть документы на квартиру, к которым обычно план приложен. В них, кстати, можно посмотреть общий метраж принадлежащего вам жилья.
Наше жилье редко бывает идеально квадратным или идеально прямоугольным. Обычно в помещении имеются ниши, выступы, вентиляционные конструкции или сантехнические элементы. Если вы пытаетесь понять, как посчитать квадратуру комнаты с нишами, то придется нарисовать их на плане.
Далее на получившемся рисунке поделите пространство на прямоугольники, треугольники, круги и замерьте их стороны. Не забывайте, что для покупки или продажи помещения площадь комнаты в квадратных метрах считается по полу. Если же вы планируете сделать ремонт и повесить натяжные потолки, расчет необходимо делать по потолку. Результаты могут незначительно отличаться из-за наличия труб, воздуховодов и др.
Когда все измерения записаны, подсчитайте площадь каждой из фигур отдельно и сложите все результаты. Если площадь считалась для себя, ее можно немного округлить.
Мы разобрали базовые формулы и постарались объяснить, как вычислить площадь комнаты в квадратных метрах. Надеемся, нам удалось вам помочь. Если же вы все еще не можете оценить размер квартиры, которую хотите продать или купить, обратитесь к нашим экспертам. Они помогут разобраться!
Прямоугольный воздуховод – обзор
1 ПОТОК ЖИДКОСТИ
Полностью разработанный профиль скорости для прямоугольных воздуховодов был определен с использованием аналогии с функцией напряжения теории упругости (Тимошенко и Гудье [72]) Драйдена и др. . [4] и Марко и Хан [70]. Рассмотрим поперечное сечение прямоугольного воздуховода, характеризующееся его соотношением сторон α * = 2 b /2 a , как показано на рис. 36, с направлением потока вдоль оси x (перпендикулярно плоскости бумаги. ).
РИС. 36. Прямоугольный воздуховод.
Профиль скорости, полученный в результате решения уравнения. (4) с граничным условием уравнения. (6) равно
(332) u = −16c1a2π3∑n = 1,3,… ∞1n3 (−1) (n − 1) / 2 [1 − ch (nπy / 2a) ch (nπb / 2a) ] cos (nπz2a)
(333) um = −c1a23 [1−192π5 (ab) ∑n = 1,3,… ∞1n5tanh (nπb2a)]
Этот профиль скорости отлично согласуется с экспериментальными результатами Холмса. и Vermeulen [383] и Muchnik et al. [384].
Поскольку уравнение. (332) связано со значительной вычислительной сложностью, Пурдей [124] предложил простую аппроксимацию в следующей форме для соотношения сторон α * ≤ 0.5:
(334) uumax = [1- (yb) n] [1- (za) m]
, где n = 2 и m получается, применяя принцип минимального рассеивания энергии, как 2.37, 3.78, 5.19, 6.60, 13.6 и ∞ для α * = 2 b / 2 a = 0.5, 1/3, 0.25, 0.20, 0.10 и 0 соответственно. Холмс и Вермёлен [383] представили значения m и n , основанные на экспериментальных измерениях градиента скорости на стене и площади под кривой профиля скорости.Натараджан и Лакшманан [385] решили уравнение импульса (4) методом конечных разностей и согласовали профиль скорости с эмпирическим уравнением (334), чтобы получить м и n как
(335) m = 1,7 +0,5 (α *) – 1,4
(336), (337) n = {2 для α * ≤1 / 32 + 0,3 (α * −1 / 3) для α * ≥1 / 3
Интегрирование уравнения. (334) по поперечному сечению воздуховода дает
(338) uum = (m + 1m) (n + 1n) [1− (yb) n] [1− (za) m]
(339) umaxum = ( m + 1m) (n + 1n)
. Значения m и n , полученные Натараджаном и Лакшмананом, профили продуктивности хорошо согласуются с экспериментальными результатами Холмса и Вермёлена [383].Приблизительное значение u max / u m по формуле. (339) находятся в пределах 0,9% от тех точных значений в Таблице 39. Натараджан и Лакшманан также представили в закрытом виде формулу для f Re как функции от α *, что находится в пределах ± 4,5% от точных значений в Таблице 42. Более точная формула для f Re представлена формулой. (341).
ТАБЛИЦА 39. ПРЯМОУГОЛЬНЫЕ КАНАЛЫ: u макс. / u м , K d (∞) И K e (∞) ДЛЯ ПОЛНОСТЬЮ РАЗРАБОТАННОГО ЛАМИНАРНОГО ПОТОКА13 (ИЗ LUNDGREN и др. [51]) ТАБЛИЦА 42. ПРЯМОУГОЛЬНЫЕ КАНАЛЫ: f Re, Nu H , Nu T , 1 и Nu H 2 ДЛЯ ПОЛНОСТЬЮ РАЗРАБОТАННОГО ЛАМИНАРНОГО ПОТОКА, ДЛЯ ВСЕХ ЧЕТЫРЕХ СТЕН ПЕРЕДАЧА ТЕПЛА (ИЗ ШАХА И ЛОНДОНА [13]) Lundgren et al. [51] определено u max / u m , K d (∞) и K e (∞), которые представлены в таблице 39. Eckert and Ирвин [386 387] был одним из первых исследователей, которые определили значение [( K (∞) + 1] для прямоугольных и треугольных каналов.Их графические значения K (∞) для прямоугольных каналов варьировались от 2,0 для α * = 1 до 0,66 для α * = 0. Значения K (∞), полученные разными исследователями, сравниваются в таблице 40. Аналитические значения K (∞) Миллера и Хана [158] наиболее близко согласуются с экспериментальными значениями Beavers et al. [388]. K (∞) из Lundgren et al. [51] выше экспериментальных значений, как указано на стр. 43. Хан [154] предсказывает быстрое развитие потока, и его K (∞) также слишком высоки. ТАБЛИЦА 40. ПРЯМОУГОЛЬНЫЕ КАНАЛЫ: K (∞) ДЛЯ ПОЛНОСТЬЮ РАЗРАБОТАННОГО ЛАМИНАРНОГО ПОТОКА прямоугольный вход Hydrod Длина Hydrod. различных исследователей сравниваются в Таблице 41. L hy + для всех данных в Таблице 41 определяется как безразмерная длина воздуховода, необходимая для достижения средней скорости, равной 99% от соответствующего полностью развернутого значения. L hy + Вигинтона и Далтона [168] являются наиболее точными; результаты Флеминга и Воробья [166] основаны на графических результатах; у Хана [154] низкие из-за его рассчитанного быстрого развития потока; а у МакКомаса [48] слишком низкие, как упоминалось на стр. 42. ТАБЛИЦА 41. ПРЯМОУГОЛЬНЫЕ КАНАЛЫ: Lhy + ДЛЯ ПОЛНОСТЬЮ РАЗРАБОТАННОГО ЛАМИНАРНОГО ПОТОКА (340) fRe = −8c1a2um [1+ (a / b)] 2 Коэффициенты трения были точно рассчитаны по формуле. (340) Шаха и Лондона [13]. Поскольку ряд уравнения.(333) быстро сходится, семизначная точность была установлена для f Re путем принятия до 30 членов. Результаты представлены в Таблице 42 и на Рис. 37. Коэффициенты f Re по Ши [108], определенные методом точечного согласования, превосходно согласуются с таковыми в Таблице 42. Коэффициенты f Re Таблицы 42 можно аппроксимировать следующим уравнением: ФИГ. 37. Прямоугольные воздуховоды: f Re и K (∞) для полностью развитого ламинарного потока. (341) fRe = 24 [1−1.3553α * + 1.9467α * 2−1.7012α * 3 + 0.9564α * 4−0.2537α * 5] Это уравнение предсказывает f Re выше не более чем на 0,05% по сравнению с данными в таблице 42. Rothfus et al. [389] представил полностью разработанный коэффициент трения как функцию аспектного отношения и числа Рейнольдса для ламинарного, переходного и турбулентного режимов течения. Для ламинарного потока представленные коэффициенты f Re такие же, как и в таблице 42.Соответствующие константы функциональных соотношений для переходного и турбулентного режимов течения были получены из экспериментальных данных и представлены графически. Для полностью развитого потока коэффициент трения зависит не только от числа Рейнольдса (например, f Re = K f , постоянная величина), но также зависит от формы поперечного сечения воздуховода ( см. Таблицу 138). Тирунараянан и Рамачандран ввели понятие фактора формы, как описано ниже, для корреляции коэффициентов f Re для прямоугольных каналов [390] и равнобедренных треугольных каналов [391]. Поле потока в некруглом воздуховоде с углами делится на столько областей потока, сколько углов. Предполагается, что на поток в каждой такой области влияет свой угол. Каждая область затем рассматривается как отдельный канал для потока с его характерным размером как длина пути наименьшего сопротивления сдвигу в поле потока, соединяющего угол и точку максимальной скорости. Средний характерный размер некруглого воздуховода, B¯, принимается как среднее арифметическое характерных размеров всех областей потока.Коэффициент формы , характеризующий геометрию воздуховода, определяется как отношение вышеуказанного среднего размера к периметру воздуховода. Прямоугольный воздуховод, показанный на рис. 36, имеет четыре идентичных области потока, одна из которых – OABC. Характерным размером для области OABC является линия ODB. Исходя из геометрии, (342) ODB = a + b (2−1) = B¯ (343) B¯P = a + b (2−1) 4 (a + b) = 1 + α * (2−1) 4 (1 + α *) Тирунараян и Рамачандран [390] получили следующую корреляцию для прямоугольных каналов: (344) fRe = 14.227 + 1402,5 (B¯P − 28) 1,90 Коэффициенты f Re, рассчитанные по этому уравнению, немного ниже, чем в таблице 42, с максимальной разницей всего 1,7% для прямоугольного воздуховода α * = 0,2. Полностью развитый градиент давления в воздуховоде зависит от площади поверхности контакта. Отношение полностью развитого градиента давления в прямоугольном воздуховоде к градиенту давления в круглом воздуховоде с той же площадью потока будет тогда зависеть от отношения периметра. Для этого Натараджан и Лакшманан [392] предложили уравнение (345) (dp / dL) r (dp / dL) c = 0.861 (PrPc) 2,75 , где суффиксы r и c обозначают прямоугольные и круглые воздуховоды соответственно. Экспериментальные значения f Re нескольких исследователей, на которые ссылаются Rothfus et al. [389], согласны с формулой. (345) в пределах 4%. Из этого уравнения очевидно, что падение давления в прямоугольном воздуховоде с любым соотношением сторон больше, чем в круглом воздуховоде с той же площадью поперечного сечения; коэффициент перепада давления составляет 1,20 и 4,30 для α * = 1 и 0,125 соответственно.Уравнение (345) можно выразить через f Re и α *, используя ( f Re) c = 16, как (346) (fRe) r = 8,968 (1 + α * α * ) 0,75 Это уравнение согласуется с коэффициентами f Re из таблицы 42 в пределах 6% для α * ≥ 0,125. Формулы, установленные для расчета потери давления:
устанавливается для воздуховодов круглого сечения.Это лучшая форма
адаптирован, потому что дает наибольшее сечение по заданному периметру. На практике, например, по причинам непроходимости или эстетики,
встречается с другими формами сетей, используемых, в частности, для передачи
воздух, очищенный в установках распределения кондиционирования. Для этого следует прибегнуть к концепции гидравлического диаметра, соответствующего
к эквивалентному диаметру или действительно используются в случае круглого
канал. Чеси около 1820 г. установил теоретическое соотношение для протоков
неуказанная форма: с: На основе формулы Чеси гидравлический диаметр для
прямоугольный воздуховод рассчитывается с помощью следующего выражения: С: Если в турбулентном потоке средняя скорость практически однородна
в любой точке участка трубопровода при ламинарном потоке, т. е.
значительно меньше. Рекомендуется проявлять большую осмотрительность, когда планируешь
прибегать к концепции диаметра гидравлического в случае ламинарного
поток. По этой причине полезно использовать другие формулы вычисления
основан на концепции эквивалентного диаметра. В случае использования трубопровода прямоугольного сечения эквивалентный диаметр можно получить, например, выражением ASHRAE: В случае использования продолговатых воздуховодов эквивалентный диаметр составляет
получено выражением ASHRAE: С: Последнее обновление: Вычислители воздуховодов – очень полезный инструмент для определения размеров воздуховодов.Вы можете использовать эти расчеты, чтобы найти правильный размер воздуховода на основе CFM или FPM. Расчеты также позволяют легко найти квадратный эквивалент круглого воздуховода или круглый эквивалент квадратного воздуховода. Используйте следующую формулу для определения размера воздуховода для надлежащего CFM: Площадь круга диаметром 12 дюймов = π6² = 113 кв. Дюймов (закругленная) Рассчитайте площадь для квадрата или прямоугольника, используя (длина * ширина). Рассчитайте площадь скругления, используя (π * радиус²). При расчете размеров воздуховодов помните, что воздуховоды не делаются стандартными круглыми 11,5 дюйма или прямоугольными 12,375 * 14,24 дюйма, поэтому вам необходимо округлить размер до ближайшего четного числа, в результате чего получится круглый диаметр 12 дюймов и Воздуховод прямоугольный 12 * 14. Каждый раз, когда вы изменяете размер воздуховода по сравнению с размером, указанным в инженерном проекте, это должно быть сделано с целью улучшения конструктивности. По возможности рекомендуется использовать проект инженера, если вы не можете сделать это из-за полевых условий. Если полевые условия не позволяют рассчитать размер, вам необходимо написать запрос на информацию (RFI), чтобы проинформировать инженера о вносимых изменениях. Система воздуховодов является важнейшим компонентом техники кондиционирования и вентиляции. Его функция состоит в том, чтобы передавать отрегулированный воздух к оконечному оборудованию с максимальной эффективностью в соответствии с расчетным потоком. Обычно поперечное сечение воздуховода имеет три формы: прямоугольную, круглую и сплюснутую. Изготовление воздуховодов прямоугольного сечения обычно осуществляется путем клепки четырех стальных пластин. Круглый воздуховод изготавливается путем наматывания стальной пластины шириной 137 мм на спирально-формовочной машине.Сплюснутые протоки встречаются относительно редко. Обычно они образуются путем сжатия воздуховодов круглого сечения. До 1960 года из-за простоты производственного процесса и небольшого пространства для установки в большинстве систем вентиляции использовались прямоугольные воздуховоды. С успешной разработкой машин для формовки больших спиральных круглых каналов большое количество инженерных примеров доказало, что круглые воздуховоды намного лучше прямоугольных с точки зрения экономии и других технических параметров. Большое количество воздуховодов из волокнистой ткани, представленных в настоящее время на рынке, представляют собой системы распределения воздуха, которые объединяют такие функции, как вентиляционные отверстия, каналы подачи воздуха, камеры статического давления, теплоизоляционные материалы и демпферы. Преимущества точной и равномерной подачи воздуха, легкого монтажного блока, высокого внешнего вида, антибактериальной устойчивости и устойчивости к плесени были получены пользователями и широко используются. Формы воздуховодов из волокнистой ткани могут быть круглыми, полукруглыми, четвертькруглыми, овальными и полуовальными, чтобы соответствовать требованиям различных строительных конструкций. Канал круглого сечения из ткани Таблица 1: Ежегодная доля рынка круглых воздуховодов: С точки зрения перспективы В рамках экономического анализа все затраты на систему воздуховодов в здании на протяжении всего срока службы можно разделить на: Результаты зарубежных исследований показывают, что по многим параметрам системы круглых воздуховодов работают лучше, чем системы прямоугольных воздуховодов. В этой статье будут обобщены результаты этих исследований и сделана попытка сосредоточить сравнение на экономическом сравнении систем воздуховодов. В то же время, поскольку стоимость обновления составляет небольшую часть общей стоимости при нормальных обстоятельствах, эта часть стоимости будет проигнорирована в данном обсуждении. Отчасти причина того, почему первоначальные инвестиции, необходимые для системы круглых воздуховодов ниже, чем для системы прямоугольных воздуховодов, заключаются в следующем: Мы разработали две проектные схемы системы вентиляции большого помещения с использованием воздуховодов круглого и прямоугольного сечения, а также сравнили высоту потери давления в системе и соответствующие экономические параметры.См. Рисунок 1 (Примечание: экономический анализ основан на ценах на рынке Скандинавии за год). Результаты расчетов показывают, что при тех же условиях конечного оборудования общая стоимость монтажа круглого воздуховода составляет только половину от прямоугольного воздуховода, а стоимость материала круглого воздуховода составляет 80% от прямоугольного воздуховода. Общая стоимость установки: 0,51R Общая стоимость материалов: 0.8M (A) Общая стоимость установки: Общая стоимость материалов: M (B) Рисунок 1: Сравнение проектных схем воздуховодов (A) Круглый воздуховод (B) Прямоугольный воздуховод Экономический анализ пространства, занимаемого системой воздуховодов, затруднен, поскольку он зависит от конструкции и назначения здания. Вообще говоря, одна из основных причин использования прямоугольных воздуховодов – это экономия места.Но на самом деле для прямоугольных воздуховодов с близким соотношением сторон фактическая площадь, занимаемая ими, больше, чем у круглых воздуховодов. Это в основном связано с тем, что для прямоугольных воздуховодов для соединения требуются фланцы, а высота кромок фланцев обычно превышает 20 мм, см. Рисунок 2 (A). Современный спиральный воздуховод можно соединять со стандартной гибкостью, см. Рисунок 2 (B). Этот метод не только не требует дополнительного места, но и проще в установке. Следовательно, для прямоугольных воздуховодов с соотношением сторон, близким к 1, преимущества круглых воздуховодов не могут быть заменены. Рисунок 2: Сравнение схемы соединения воздуховода (A) Прямоугольный воздуховод (B) Круглый воздуховод Вместо прямоугольных воздуховодов с большим соотношением сторон можно использовать несколько круглых воздуховодов, как показано на Рисунке 3. Это Альтернатива может значительно упростить контроль объема воздуха. При этом значительно снизятся и затраты на установку. Хотя стоимость материалов может увеличиться, однако обследование показало, что при этой схеме первоначальные вложения почти такие же, как и при прямоугольном воздуховоде. Рисунок 3: Альтернативный план замены прямоугольного воздуховода 550 мм × 150 мм двумя круглыми воздуховодами D = 200 мм При нормальных обстоятельствах большая часть эксплуатационных расходов на воздух системы кондиционирования – потребление энергии. Затраты на энергию включают энергию, потребляемую для нагрева или охлаждения воздуха, а также для транспортировки этого воздуха к конечному оборудованию. Если вся система воздуховодов хорошо изолирована, утечка воздуха из воздуховода становится важным источником избыточного потребления энергии. Для системы воздуховодов вентилятор обеспечивает циркуляцию энергии, и давление ветра вентилятора обычно не превышает 650 Па. Не считая потери давления в оконечном оборудовании вентиляционной установки, доступный напор всей системы воздуховодов составляет около 200–300 Па. Таким образом, вам следует избегать больших потерь напора в системе воздуховодов. В то же время количество утечки воздуха также напрямую влияет на выбор мощности вентилятора. Согласно теореме вентилятора, мощность вентилятора пропорциональна кубу объема воздуха, то есть, если уровень утечки воздуха через воздуховод составляет 6%, мощность вентилятора увеличится на 20%, а скорость утечки спирального кругового воздуха труба намного меньше, чем у прямоугольной воздуховода. Скорость утечки воздуха в воздуховоде можно рассчитать по следующей формуле: В Европе герметичность воздуховодов делится на четыре уровня (A, B, C, D) в соответствии с постоянной утечки воздуха. В таблице 2 показаны максимально допустимые константы утечки воздуха для соответствующих марок. Таблица 2: Классификация воздухонепроницаемости в европейских системах воздуховодов По сравнению с круглыми воздуховодами для соединения прямоугольных воздуховодов требуется гораздо больше болтов и заклепок, поэтому утечка воздуха неизбежно намного больше. Рисунок 4 представляет собой набор данных измерений в Бельгии. Данные показывают, что средняя скорость утечки прямоугольных каналов в 7 раз выше, чем у круглых. «Нормы строительства и приемки работ по вентиляции и кондиционированию воздуха» GB50243-2002 также гласят, что допустимая утечка воздуха в воздуховодах круглого сечения составляет 50% от утечки воздуха в воздуховодах прямоугольного сечения. Рисунок 4: Измерения скорости утечки воздуха в 21 бельгийском здании (Carrié et al, 1999) Гидравлический эквивалент непосредственно используется для оценки потери давления в системе прямоугольных воздуховодов для воздуховодов с таким же гидравлическим эквивалентным диаметром. Несмотря на разную форму поперечного сечения, они все равно имеют одинаковую потерю давления на всем пути. Рис. 5 Сравнение потерь давления в воздуховоде круглого сечения (D = 0,5 м, U = 5 м / с, ∑ = 0,15 мм) и прямоугольном воздуховоде с той же площадью и расходом. Очевидно, что в этом случае потеря давления в прямоугольном воздуховоде намного больше, чем в круглом воздуховоде, и по мере увеличения удлинения воздуховода потеря давления увеличивается.Это значит, что мощность вентилятора должна быть больше. Рисунок 5: Сравнение потерь давления между прямоугольным и круглым воздуховодами при постоянном расходе и скорости потока (расход = 1 м³ / с, v = 5 м / с) Концепция «гидравлического эквивалентного диаметра» основана на предположение, что среднее напряжение сдвига вдоль границы прямоугольного воздуховода должно быть согласованным. Другими словами, изокинетическая линия должна быть параллельна границе воздуховода, но фактические результаты измерений показывают, что в прямоугольном воздуховоде градиент скорости вдоль диагональной линии затухает медленнее всего, а градиент скорости вдоль центральной линии затухает самым медленным. .Поэтому теоретически гидравлический эквивалентный диаметр следует использовать с осторожностью в следующих двух случаях. Экспериментальные данные также ставят под сомнение универсальность гидравлического эквивалентного диаметра. ДЖОНС провел серию экспериментов по потере давления в гладких прямоугольных воздуховодах.Я повторно проанализировал его экспериментальные данные, как показано на рисунке 6. Несмотря на отсутствие данных для 10 <соотношение сторон <25, данные на рисунке 6 по-прежнему убедительно свидетельствуют о монотонно возрастающем влиянии отношения длины к ширине на потерю гидравлического эквивалентного диаметра давления. Эксперименты Григсетала с грубыми прямоугольными воздуховодами дали аналогичные результаты. Рисунок 6: Сравнение потерь давления между гладким прямоугольным воздуховодом и круглым воздуховодом с различным соотношением длины и ширины Во избежание проблем в зданиях необходимо регулярно чистить воздуховоды. Методы уборки включают сухой (с помощью пылесоса и щетки) или влажный (с помощью длинной швабры). В обоих случаях чистить круглые воздуховоды проще, чем прямоугольные. Экономический анализ систем воздуховодов – сложная задача. При этом необходимо учитывать множество факторов, а срок службы системы воздуховодов может превышать десять лет.В этом случае небольшое улучшение дизайна и качества может повысить рентабельность инвестиций. В связи с этим использование воздуховодов круглого сечения должно быть более экономичным решением. Наконец, следует отметить, что из соображений тишины и простора прямоугольные воздуховоды по-прежнему рекомендуются для некоторых крупнопоточных и крупногабаритных частей системы воздуховодов, таких как впускные отверстия для всасывания свежего воздуха и устройства для обработки воздуха. торговые точки. Несмотря на то, что круглые воздуховоды требуют наименьшего количества материала для данной скорости потока и
допустимый перепад давления, прямоугольные воздуховоды обычно предпочтительны на практике, так как
они легко вписываются в конструкцию здания, занимая меньше места, и они
также легко изготовить.Отношение двух сторон «a» и «b» прямоугольника (a / b) равно
называется соотношение сторон воздуховода. Поскольку квадратные воздуховоды с соотношением сторон 1,0
близок по характеристикам к воздуховоду круглого сечения, предпочтительно использовать максимально близкое соотношение сторон
к единству, насколько это возможно для лучшей производительности. Таблицу трения для воздуховодов круглого сечения можно использовать для оценки
падение давления в прямоугольном воздуховоде эквивалентного диаметра. А
Прямоугольный воздуховод считается эквивалентным круглому воздуховоду, если объемный расход Qair и падение давления на трение на единицу длины (ΔPf / L) одинаковы для
оба.Приравнивая эти два параметра для воздуховода прямоугольного сечения и эквивалентного
воздуховод круглого сечения, можно показать, что эквивалентный диаметр определяется по формуле: Вышеприведенное уравнение действительно для формата изображения, меньшего или равного
к 1: 8. Таким образом, исходя из известных значений двух сторон воздуховода «a» и «b», можно
найти эквивалентный диаметр Deq. Из эквивалентного диаметра и расхода воздуха
можно оценить падение давления на единицу длины при трении с помощью диаграммы трения.Однако при использовании эквивалентного диаметра и расхода
чтобы найти падение давления на трение из диаграммы, значения скорости, указанные на
диаграммы не являются фактическими скоростями. Фактические скорости должны быть получены из
расход и фактическая площадь поперечного сечения прямоугольного воздуховода. Если
прямоугольный воздуховод должен быть рассчитан на заданный расход и заданное трение
перепад давления, то можно сначала найти эквивалентный диаметр из таблицы трения, а затем найти требуемые размеры воздуховода либо путем фиксации
соотношение сторон или одну из сторон. • СЛЕДИТЬ • ПОДЕЛИТЬСЯ • ОТЧЕТ Скорость воздушного потока в воздуховоде неодинакова по поперечному сечению воздуховода. Это связано с тем, что трение о стенки воздуховода приводит к тому, что скорость воздуха по бокам ниже, чем скорость в центре, создавая параболический профиль скорости. Вентиляторы, уголки, фитинги воздуховодов, тройники и змеевики создают турбулентность в воздуховоде, дополнительно изменяя скорость по поперечному сечению.Показания всегда следует снимать при диаметрах воздуховода не менее 8 и 1/2 на входе и 1 и 1/2 диаметров канала после любого устройства или проникновения, которое может вызвать турбулентность. Исходя из этих условий, скорость воздуха должна быть усреднена по поперечному сечению воздуховода, чтобы получить точное измерение. Чтобы получить среднюю скорость воздуха, по поперечному сечению воздуховода берется формальный набор точек измерения. Они известны как показания хода. Существует два основных режима считывания показаний траверса: равноплощадочный и логарифмически линейный. Для прямоугольных воздуховодов методом равных площадей поперечное сечение делится на маленькие прямоугольники равной площади. Скорость берется в центральной точке каждого из этих прямоугольников, а затем усредняется для получения скорости в воздуховоде. При использовании этого метода минимальное количество точек считывания составляет 16, а максимальное – 64. Если снимается менее 64 точек считывания, расстояние между точками не должно превышать 6 дюймов. В показанном примере в стенке воздуховода просверливаются 4 отверстия, и в каждое отверстие вставляется трубка Пито или анемометр для снятия четырех показаний, пересекающих ширину или высоту воздуховода.Точки чтения находятся в центре каждого прямоугольника. Для круглых воздуховодов, использующих метод равных площадей, скоростное давление следует брать в центре равных концентрических площадей и усреднять. В показанном примере просверливаются два отверстия по средней линии воздуховода. Один набор точек считывания берется по вертикали, а второй – по горизонтали. Если диаметр воздуховода больше 14 дюймов, используйте 20 точек отсчета; если он составляет от 10 до 14 дюймов в диаметре, используйте 16 точек отсчета; и если он меньше 10 дюймов в диаметре, используйте 10 точек считывания с половиной точек на каждой плоскости считывания.Площадки для чтения не обязательно должны быть вертикальными и горизонтальными, но они должны располагаться под углом 90 градусов друг к другу. Используйте приведенные формулы для глубины погружения каждого показания в соответствии с радиусом воздуховода. При использовании трубки Пито скорость прямо пропорциональна скоростному давлению и может быть рассчитана по формуле, показанной для воздуха с V (скорость), d (плотность воздуха в приложении) и hv ( скорость давления от измерительного устройства). По скорости легко вычислить объемный расход, если расход Q равен скорости, умноженной на площадь поперечного сечения воздуховода или трубы. Компания Dwyer Instruments, Inc. имеет на веб-сайте калькулятор скорости и расхода воздуха. Его также можно загрузить как мобильное приложение для устройств iOS® и Android®. Этот калькулятор будет использовать скоростное давление для расчета скорости и расчета объемного расхода воздуха с учетом площади поперечного сечения. Он также предлагает возможность корректировать плотность воздуха в зависимости от уровня влажности. Для получения более подробной информации, пожалуйста, ознакомьтесь с Американским обществом инженеров по отоплению, охлаждению и кондиционированию воздуха (ASHREA), Национальным бюро экологического баланса (NEBB), стандартами Международной ассоциации движения и контроля воздуха (AMCA) или Национальным советом по балансировке (NBC). Если вы хотите найти гидравлический радиус в расчетах расхода в трубе, то этот калькулятор гидравлического радиуса – это то, что вам нужно. Мы собрали в общей сложности пять уравнений гидравлического радиуса для различных форм каналов: прямоугольник, трапеция, треугольник и труба с разным уровнем заполнения – этот инструмент определенно не несбыточная мечта! Войдите и узнайте, в чем разница между диаметром более влажного и гидравлическим радиусом трубы или любой другой формы канала в этом отношении! Гидравлический радиус, Например, представьте, что у вас есть прямоугольный канал, такой же, как на изображении.Площадь потока будет равна ширине канала b , умноженной на глубину потока, y . С другой стороны, смоченный периметр – это просто общая длина стенок канала, которые контактируют с жидкостью . В случае прямоугольного канала это сумма b + y + y . Смачиваемый периметр трубы – это часть всего периметра трубы, которая контактирует с текущей жидкостью (например, водой).Рассчитать это для полной трубы очень просто – она равна общему периметру трубы: Если ваша труба заполнена только наполовину, смоченный периметр будет равен половине всего периметра: Что произойдет, если труба заполнена не совсем или наполовину? В этом случае смоченный периметр равен длине дуги, соответствующей центральному углу θ, как показано на рисунке. Этот гидравлический калькулятор радиуса может использоваться для каналов различной формы, включая прямоугольники, трапеции и треугольники.Давайте проанализируем их более подробно, чтобы выяснить, какие уравнения гидравлического радиуса можно использовать в каждом конкретном случае. 1. Канал прямоугольный В случае прямоугольного канала формулы очень просты. Гидравлический радиус просто равен площади прямоугольника, деленной на периметр смачивания, как объяснено в первом примере: Вот и все – вы можете использовать эту формулу, чтобы найти гидравлический радиус прямоугольного открытого канала. 2. Канал трапециевидный Мы можем упростить эту формулу, используя значение наклона z , определяемое как усиление ширины канала на каждую единицу его глубины (градиент непараллельных сторон трапазоида). Подобно правилу треугольника, увеличение ширины на одной стороне трапеции составляет Смачиваемый периметр равен b и длинам двух наклонных сторон канала. Используя теорему Пифагора, находим: Отсюда можно сделать вывод, что: 3. Канал треугольный Мы можем записать площадь треугольника двумя способами: одним способом, использующим стороны треугольника, и другим, который использует наклон, z : Смоченный периметр треугольника аналогичен периметру трапеции, но на этот раз мы суммируем только наклонные стороны канала: Наконец, мы приходим к уравнению гидравлического радиуса треугольника: Остальные четыре параметра в нашем гидравлическом калькуляторе радиуса помогают анализировать трубы.Поскольку формулы различаются, мы выделили два разных случая: канал заполнен, а другой – меньше, чем заполнен. 1. Труба полная Нет ничего проще, чем найти гидравлический радиус трубы, полностью заполненной жидкостью. Все, что вам нужно сделать, это использовать формулы для площади и периметра круга! Как видите, гидравлический радиус полной трубы равен половине ее радиуса . 2. Трубка (неполная) Проблема немного усложняется, когда труба заполнена только частично. Мы уже рассчитали этот смачиваемый периметр по смачиваемому периметру участка трубы: А что насчет области тогда? Вы можете использовать формулу для площади сегмента круга: Комбинируя эти два, мы находим уравнение гидравлического радиуса: Это настоящая формула! К счастью, вы можете использовать этот удобный гидравлический калькулятор радиуса вместо того, чтобы тщательно выполнять все вычисления вручную;) α * umax um K d (∞) K e (∞) 1.000 2,0962 1,3785 2,1541 0,750 2,0774 1,3727 2,1329 0,500 1,99114 0114 1,9690 0,250 1,7737 1,2876 1,8256 1/6 1,6758 1.2600 1,7325 0,125 1,6283 1,2454 1,6848 0,100 1,6009 1,2365 1,6009 1,2365 1,6560 0 1,5000 1,2000 1,5429 α * fRe Nu T Nu h2 Nu h3 1.000 14.22708 2,976 3,60795 3,091 0,900 14,26098 – 3,62045 – – 0,800 14,37780 – 3.66382 – 0,750 14,47570 – 3,70052 – 14.06482 3,077 3,73419 – 0,700 14.60538 – 3,74961 – 3,74961 0,600 14,97996 – 3,89456 – 0,500 15,54806 3,391 4,12330 3.02 0,400 16,36810 – 4,47185 – 1/3 17,08967 3,956 4,794803 4.98989 – 0,250 18,23278 4,439 5,33106 2,94 0.200 19.07050 – 73769 2,93 1/6 19,70220 5,137 6,04946 2,93 1/7 20,19310 – 20,19310 – 5,597 6,49033 2,94 1/9 20, – 6,65106 2,94 1/10 21.16888 – 6.78495 2.95 1/12 21.58327 – 6.99507 – 1/15 1/20 22,47701 – 7,45083 – 1/50 23,36253 – 7, – 9009 000
7,541 8,23529 8,235 α * Miller Han [158] Fleming Sparrow [166] Wiginton Dalton [168] [51] Han [154] Beavers et al. [388] 1 1,433 – 1,63 1,552 2,02 1,31 0,750 – – 1 – 1 – 1 – 1520 2,00 1,21 0,500 1,281 1,46 1,44 1,383 1,80 1,18 0,23 – 0,200 0,931 0,96 1,01 – – 0,88 0,125 – – – 879 1,10 0,72 0 0,658 0,65 – 0,686 0,85 0,60
м (333), f Re для прямоугольных каналов может быть выражено в замкнутой форме как α * Вигинтон Дальтон [168] Fleming Sparrow [166] Han [154] McComas [48] 1 0.09 – 0,0752 0,0324 0,750 – – 0,0735 0,0310 0,500 0,085 0,085 0,085 0,075 – 0,0427 0,0147 0.200 0,08 0,08 – – 0.125 – – 0,0227 0,00938 0 – – 0,0099 0,00588 Расчет, chsy, диаметр, гидравлический, продолговатый, канальный, воздушный, проточный, эквивалент
Создание калькуляторов воздуховодов – HVAC / R и солнечная энергетика
Формулы для определения размеров воздуховодов
CFM = Площадь * FPM
Пример: 12 * 12 воздуховодов при 750 футах в минуту; 12 * 12 = 1 кв. Фут
1 кв. Фут * 750 футов в минуту = 750 кубических футов в минуту
Используйте следующую формулу, чтобы изменить форму воздуховода с круглой на квадратную:
Площадь круга = πr²
Площадь / длина = ширина
Пример. Преобразование круглого воздуховода 12 дюймов в квадратный канал глубиной 10 дюймов или прямоугольный воздуховод
.
113/10 = 11,3
Круглый воздуховод 12 дюймов = прямоугольный воздуховод 10 * 11,3. Используйте прямоугольный воздуховод 10 * 12
.
Используйте следующую формулу, чтобы изменить форму воздуховода с квадратной на круглую:
2 (квадратный корень [площадь / π]) = диаметр
Пример. Преобразование квадратного воздуховода 10 * 10 в эквивалентный круглый воздуховод
.
Площадь = 10 * 10 = 100 кв. IN
2 (квадратный корень [100 / 3,14159]) = 2 (квадратный корень [31.83])
= 2 (5,6418) 5 11,28
Квадратный воздуховод 10 * 10 = круглый воздуховод 11,28 ″. Используйте стандартный воздуховод
диаметром 12 дюймов. Указания по выбору размеров воздуховодов
Связанные для вас 7 причин, почему круглые воздуховоды лучше прямоугольных
1.Справочная информация Страна 1960 1965 1970 1975 1980 1985 1990 2000 Скандинавский 5 15 40 60 70 80 85 90 Германия 5 5 9011 20 25 25 50 Франция 5 10 20 30 40 50 50 65 Англия 5 Англия 15 20 25 35 35 55 Полная потеря давления (Па): 150,0 Полная потеря давления (Па): 165,4 Класс A KA = 0,027 × 10 -3 м 3 с -1 м -2 Па -0,65 Класс B 3 KB = 0,009 × 10 -3 м 3 с -1 м -2 Па -0,65 Класс C KC = 0.003 × 10 -3 м 3 с -1 м -2 Па -0,65 Класс D KD = 0,001 × 10 -3 м 3 с -1 м -2 Па -0,65 Прямоугольные воздуховоды – эквивалентный диаметр
Пересечение воздуховодов для определения средней скорости и объема воздуха – Блог Dwyer Instruments
| Смачиваемый периметр
Что такое гидравлический радиус?
R , определяется как отношение площади поперечного сечения потока, A , к периметру смачиваемого канала, P : R = A / P Как рассчитать смоченный периметр трубы?
P = 2πr P = πr θ = 2 * arccos [(r - h) / r] P = r * θ Уравнение гидравлического радиуса для прямоугольного, трапециевидного и треугольного канала
R = A / P = (b * y) / (b + y + y) = (b * y) / (b + 2y) A = y * (B + b) / 2 zy , и, следовательно, B = b + 2zy .Затем A = by + y²z P = b + 2 * y * √ (1 + z²) R = A / P = (by + y²z) / [b + 2 * y * √ (1 + z²)] A = B * y / 2 = y²z P = 2 * y * √ (1 + z²) R = A / P = y²z / [2 * y * √ (1 + z²)] = yz / [2 * √ (1 + z²)] Гидравлический радиус трубы
R = A / P = πr² / 2πr = r / 2 P = r * θ , где центральный угол θ = 2 * arccos [(r - h) / r] A = r² * (θ - sin (θ)) / 2 R = A / P = [r² * (θ - sin (θ)) / 2] / (r * θ)