Расчет площади воздуховодов и фасонных изделий
На сегодняшний день воздуховоды из стали пользуются наибольшей популярностью. В вентиляции применяются воздуховоды их оциокованнной стали толщиной 0,5-1,0мм (в зависимости от сечения), отличаются гладкой поверхностью, антикоррозийными свойствами, невысокой ценой и долговечностью. Эти воздуховоды характеризуются повышенной огнестойкостью. Применяются как в промышленных, так и в жилых зданиях, ресторанах, клубах и т.д. Жесткие воздуховоды изготавливаются из оцинкованной или нержавеющей стали как круглого, так и прямоугольного сечения, обеспечивая необходимую огнестойкость, долговечность. Применяются в помещениях любой планировки и сложности.
Возможно изготовить воздуховоды и фасонные изделия любого размера и конфигурации
|
| ||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Расчет площади воздуховода для вентиляции онлайн-калькулятор
Приведенные ниже онлайн калькуляторы помогут Вам автоматически рассчитать площадь воздуховодов и фасонных изделий, результаты расчетов выводятся в квадратных метрах!
Вычисление количества и площади воздуховодов, которые являются составной частью вентиляционной системы, – это один из главных этапов монтажа.
Все процедуры основаны на определении размерных характеристик с учетом расхода воздуха, который будет проходить через воздуховод. Нередко также требуется заранее рассчитать всю площадь воздуховодов. Эти процессы стоит рассмотреть более подробно.
Какие данные используются при расчете вентиляции?
Первоначально требуется отметить, что во внимание принимаются ключевые показатели самого сооружения. К ним относится назначение здания, внутренняя площадь комнат, число сотрудников и посетителей, которые постоянно пребывают в сооружении. Если планируется устанавливать вентиляционную систему в промышленном сооружении, обязательно учитываются особенности ведения производственного процесса. При проектировании вентиляционной системы руководствуются определенным перечнем нормативной документации. К ним относятся:
- СНиП 41-01-2003.
- СП 7.13130.2013
- ГОСТ 12.1.005-88 и пр.
Как рассчитывается площадь воздуховодов с разным сечением?
Квадратура вентиляционных труб с разными типами сечения обладает своими особенностями.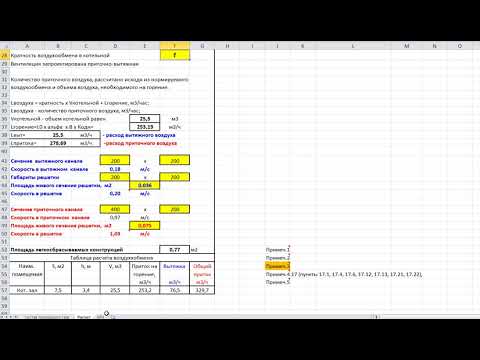
Это обязательно учитывается при расчете площади воздуховодов, так как расход воздушных масс у каждой вентиляционной системы может значительно отличаться. Это не зависит от скорости перемещения воздуха в трубах.
Осуществляя расчет систем вентиляции большой протяженности и с множеством разветвлений, обязательно учитывается уровень влажности и температура окружающего пространства, если она более +20 градусов Цельсия. Нужно учесть также аэродинамические показатели самих воздуховодов и фасонных деталей. Параметры зависят от формы изделия и материала, из которого оно изготовлено. Расчет вентиляции осуществляется с применением поправочных коэффициентов и специальных формул.
Важно знать, что параметры квадратуры вентиляционного канала и скорость перемещения воздушных масс имеют обратную пропорциональность. Если сказать иными словами, при большом сечении вентиляционной трубы требуется меньшая скорость транспортировки воздушных масс, которые нужны для обеспечения подачи необходимого объема.
Расчет площади элементов системы вентиляции осуществляется с учетом двух параметров, которые берутся из нормативно-правовой базы.
Стоит отметить, что в фактическом плане такие параметры описывают кратность обмена воздушных масс. К ним относятся:
- Расход воздушных масс (R). Параметр измеряется в м3/час.
- Скорость движения воздушных масс (V). Параметр измеряется в м/с.
В формуле, применяемой при вычислении площади воздуховодов круглого и прямоугольного сечения, используются показатели из нормативных документов. Она выглядит так:
S = R/k × V
Здесь k является коэффициентом, который равен 3600.
Есть большое количество и альтернативных формул, где оперируются другие коэффициенты, но ключевые параметры остаются неизменными. Пример:
S = R × 2,778/V
Если запланировано использовать воздуховоды с большим сечением, вы можете рассчитывать на значительное снижение шума при движении воздушных потоков. Также существенно снижаются затраты на электроэнергию, которая необходима для организации перемещения.
В этом случае материалоемкость будет существенно больше, поэтому увеличивается итоговая стоимость комплектующих деталей для вентиляционных систем.
На эффективность передвижения воздушных масс может повлиять и форма сечения воздуховодов. При прохождении прямоугольных конструкций воздушные потоки сталкиваются с большим сопротивлением, но монтировать такие воздуховоды значительно проще. Особенно это актуально при необходимости создания системы вентиляции в стесненных условиях, так как прямоугольные воздуховоды можно закрепить впритык со стенами и иными конструкциями.
Круглые изделия отличаются оптимальными аэродинамическими качествами, но не всегда способны вписаться в интерьер помещения. Имеются в продаже конструкции с хорошими эстетическими свойствами, но их покупка приведет к значительным расходам.
В качестве альтернативного варианта потребителям предлагаются воздуховоды с овальной формой. Именно они сочетают в себе оптимальную эффективность эксплуатации эргономичность.
Использование калькуляторов для расчета площади воздуховодов
Если углубиться в тематику расчета системы вентиляции, разобраться со всеми нюансами не составит труда.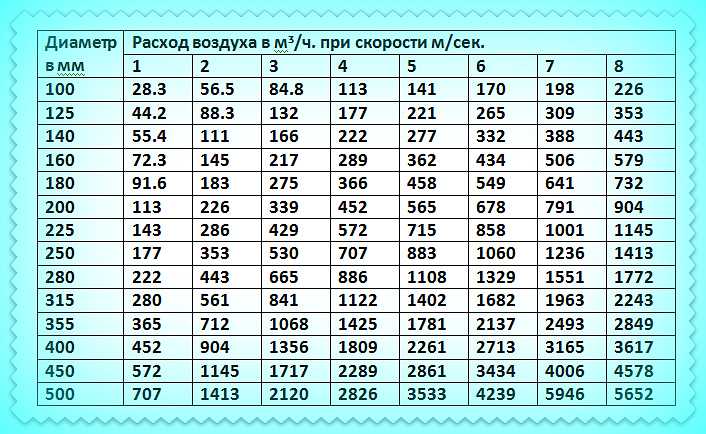
Но есть и более простой, альтернативный вариант – использование наших калькуляторов для расчета площади воздуховодов и фасонных элементов системы вентиляции (расчет осуществляется в м2). Они позволят исключить вероятность совершения ошибки, которая по итогу может обойтись дорого.
Пользоваться специальными калькуляторами для расчета квадратуры воздуховодов и фасонных элементов систем вентиляции весьма просто. Достаточно указать требуемые параметры и буквально через долю секунды вы получите показатели.
Если самостоятельно разбираться в особенностях расчета системы вентиляции нет времени, лучше обратиться к специалистам компании «ВИНТЭЛ». Они имеют большой опыт в этом направлении.
Грамотный расчёт площади воздуховода и параметров системы вентилирования, каналов для воздушных потоков позволяет создавать максимально эффективные комплексы. Правильные результаты заметно снижают расходы, связанные с приобретением материалов, закупкой электроустановок, а также последующим техобслуживанием.
Ведь вычисления способствуют бесперебойному функционированию климатического спецоборудования, включающего и вентиляторы.
Методика постоянных скоростей для определения необходимых воздуховодов
Предварительно формируется план помещений. Основываясь на нормативах, выясняется требующийся в каждой зоне объём воздуха. После этого разрабатывается схема разводки. В чертеже отмечаются места установки решёток и диффузоров. Обязательно отображение изменений сечений, а также расположение отводов. Расчёт воздуховодов осуществляется для наиболее удалённой точки вентиляционной системы, которая подразделяется на фрагменты, ограниченные разветвлениями либо решётками.
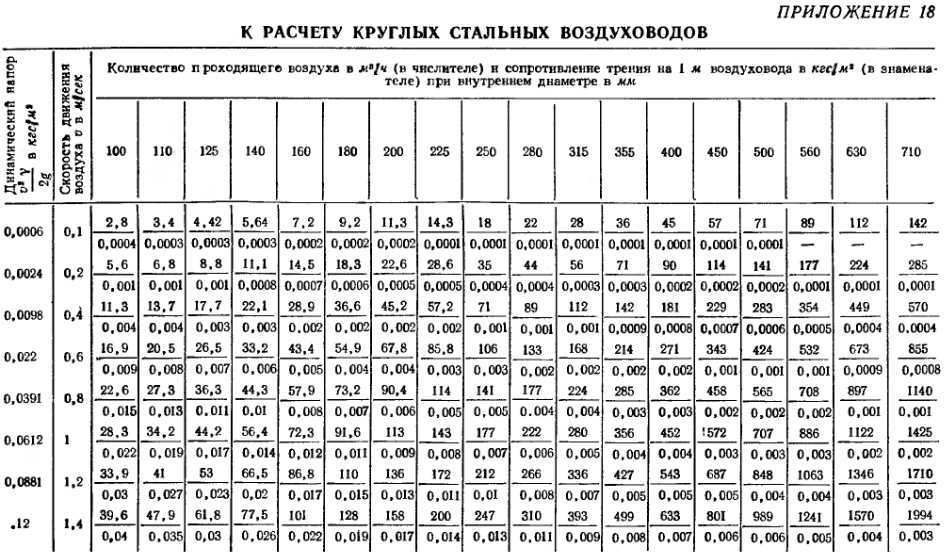
Вычисления сводятся к подбору необходимого сечения канала по всей его длине. Важно определить и потери давления, чтобы выбрать вентилятор либо подобрать приточную электроустановку. К изначальным сведениям относится объём воздушных масс, проходящих через комплекс вентиляции. Используя сделанный чертёж, производится расчёт диаметра воздуховода.
С этой целью задействуется графическая зависимость потери давления.
Каждая разновидность каналов нуждается в собственном графике. Изготовители такие сведения не скрывают, предоставляя их вместе с продукцией. Если информация отсутствует, то придётся воспользоваться справочными данными при расчете воздуховодов.
Выбор размера по номограмме
Рассматриваемый метод требует задать на каждом участке конкретную скорость воздушных потоков. Величина при расчете воздуховодов не должна выходить за границы, указанные в нормативах, регламентирующих характеристики помещения с выбранным предназначением. Магистральные воздуховоды приточной, а также вытяжной системы вентиляции обязаны обеспечивать следующие скорости:
- 3,6…5 м/с в жилых помещениях;
- ..11 м/с на промышленном объекте;
- 3,5…6 м/с на офисном пространстве.
В ответвлениях должны предусматриваться скоростные показатели:
- .
.6,5 м/с в офисах; - ..5 м/с в жилых комнатах;
- ..9 м/с на производстве.
.6,5 м/с в офисах; Если скорость превосходит допустимое значение, уровень издаваемых звуков повышается. В итоге шумы становятся некомфортными для человеческого восприятия.
Именно поэтому особенно важно произвести расчет воздуховодов онлайн на специализированном сайте.
Определившись со скоростью, переходят к поиску на графике необходимого сечения канала. Графическая зависимость содержит и от потери давления на погонный метр, показатель которого потребуется для вычислений. Общие потери давления определяются перемножением удельного значения на протяжённость фрагмента. Если возникли проблемы с расчетом воздуховодов, онлайн-калькулятор на сайте «Винтэл» поможет с ними справиться.
Основные требования к вычислению площади поверхности отвода
Система вентиляции функционирует без сбоев и максимально эффективно, если грамотно вычислена площадь воздуховодов и фасонных изделий!
Данные вычисления определяют выбор составных частей и спецоборудования.
Цель расчётов заключается в обеспечении необходимой кратности обновления воздушных масс в конкретных помещениях. При этом она должна учитывать назначение внутренних пространств.
Определяясь с результирующими характеристиками воздуховодов в м2, важно акцентироваться на том, что рассчитанная площадь каналов обязана гарантировать несколько ключевых моментов:
- Обеспечение в помещении заданного температурного режима. В пространствах с избыточным количеством тепловой энергии должно предусматриваться её отведение. При этом надлежит минимизировать тепловые потери в местах, испытывающих дефицит тепла.
- Скорость движения воздушных потоков не должна приводить к дискомфорту. Возле рабочих мест следует организовывать фильтрацию воздуха от загрязнений.
- Вредные для человеческого здоровья химические вещества, взвеси обязаны соответствовать требованиям, указанным в ГОСТ 12.1.005-88.
В отдельных помещениях обязательно постоянное поддержание подпора с исключением подачи воздушных масс извне.
Например, к ним причисляются подвалы, иные пространства, где присутствует возможность скопления небезопасных веществ.
Что еще нужно знать при расчёте площади отводов?
Производительность системы вентилирования зависит от таких параметров воздуховодов как площадь поперечного сечения, длина и форма рукавов и шахты.
Правильные вычисления площади отводов позволяют обеспечивать требуемые скоростные показатели воздушных потоков, пропускную способность, общую эффективность вентиляции.
Чтобы повысить точность расчёта площади воздуховодов в м2, целесообразнее воспользоваться онлайн-калькулятором!
Компьютерная программа точнее осуществляет вычисления, если сравнивать её с ручным способом, потому что она оперирует высокоточными числами, округлёнными до заданного разработчиком знака после запятой.
Расчёты воздуховодов в м2, осуществлённые правильно, позволяют сэкономить финансы, ведь выясняется точное количество компонентов.
Также грамотные вычисления способствуют созданию комфортных условий для работы и отдыха людей.
Посчитать площадь поверхности вентиляционных воздуховодов и фасонных частей вы можете при помощи калькуляторов, приведенных вверху данной страницы, расчет осуществляется в м2!
Калькулятор площади поверхности
Используйте приведенные ниже калькуляторы для расчета площади поверхности некоторых распространенных форм.
Площадь поверхности шара
Площадь поверхности конуса
Площадь поверхности куба
Площадь поверхности цилиндрического резервуара
Площадь поверхности прямоугольного резервуара
| |||||||||
Площадь поверхности капсулы
Площадь поверхности крышки
Для расчета укажите любые два значения ниже.
| |||||||||
Площадь конической усеченной поверхности
| |||||||||
Площадь поверхности эллипсоида
| |||||||||
Площадь поверхности квадратной пирамиды
Калькулятор связанных объемов | Калькулятор площади | Калькулятор площади поверхности тела
Площадь поверхности твердого тела является мерой общей площади, занимаемой поверхностью объекта.
Все объекты, рассматриваемые в этом калькуляторе, более подробно описаны на страницах Калькулятор объема и Калькулятор площади. Таким образом, этот калькулятор будет сосредоточен на уравнениях для расчета площади поверхности объектов и использовании этих уравнений. Пожалуйста, обратитесь к вышеупомянутым калькуляторам для более подробной информации о каждом отдельном объекте.
Сфера
Площадь поверхности (SA) сферы можно рассчитать с помощью уравнения:
SA = 4πr 2
где r — радиус
Ксаэль не любит ни с кем делиться своими шоколадными трюфелями. Когда она получает коробку трюфелей Lindt, она начинает вычислять площадь поверхности каждого трюфеля, чтобы определить общую площадь поверхности, которую ей нужно облизать, чтобы уменьшить вероятность того, что кто-нибудь попытается съесть ее трюфели. Учитывая, что каждый трюфель имеет радиус 0,325 дюйма:
SA = 4 × π × 0,325 2 = 1,327 дюйма 2
Конус
Площадь поверхности круглого конуса можно рассчитать, суммируя площади поверхности каждого из его отдельных компонентов.
«Основной SA» относится к кругу, который содержит основание в замкнутом круглом конусе, в то время как боковой SA относится к остальной части конуса между основанием и его вершиной. Уравнения для расчета каждого, а также общего SA замкнутого круглого конуса показаны ниже:
база SA = πr 2
боковой SA = πr√r 2 + h 2
общая SA = πr(r + √r 2 + h 2 )
где r — радиус, а h — высота. в ряде стран Юго-Восточной Азии. Она решает сшить свое собственное и, будучи очень практичным человеком, не погрязшим в сентиментальности, достает свадебное платье своей матери из темных ниш шкафа, в котором оно находится. Она определяет площадь поверхности материала, которая ей нужна для создания шляпы радиусом 1 фут и высотой 0,5 фута, следующим образом:
поперечная SA = π × 0,4√0,4 2 + 0,5 2 = 0,805 фута 2
Куб
СА = 6а 2
где a — длина ребра
Анна хочет подарить своему младшему брату кубик Рубика на день рождения, но знает, что у ее брата короткая продолжительность концентрации внимания и он легко расстраивается.
Она заказывает кубик Рубика, в котором все грани черные, и должна заплатить за настройку в зависимости от площади поверхности кубика с длиной ребра 4 дюйма.
SA = 6 × 4 2 = 96 дюймов 2
Цилиндрический резервуар
Площадь поверхности закрытого цилиндра можно рассчитать, суммируя площади его основания и боковой поверхности:
основание SA = 2πr 2
боковой SA = 2πrh
общая СА = 2πr(r + h)
где r — радиус, а h — высота
У Джереми есть большой цилиндрический аквариум, в котором он купается, потому что он не любит душ или ванну. Ему любопытно, остывает ли его нагретая вода быстрее, чем в ванне, и ему нужно рассчитать площадь поверхности его цилиндрического резервуара высотой 5,5 фута и радиусом 3,5 фута.
общая SA = 2π × 3,5(3,5 + 5,5) = 197,920 футов 2
Прямоугольный резервуар
Площадь поверхности прямоугольного резервуара равна сумме площадей каждой из его сторон:
SA = 2лв + 2лв + 2вч
где l — длина, w — ширина, h — высота
Банана, старшая дочь в длинной череде банановых фермеров, хочет научить свою избалованную гнилую младшую сестру, Банан-Хлеб, урок о надежде и ожиданиях.
Banana-Bread всю неделю требовала новый набор ящиков для своих новых фигурок Бэтмена. Таким образом, Банана покупает ей большой кукольный дом Барби с кухонной утварью ограниченного выпуска, духовкой, фартуком и реалистичными гниющими бананами для Бэтмена. Она упаковывает их в прямоугольную коробку тех же размеров, что и ящик, который хочет Banana-Bread, и ей нужно определить количество оберточной бумаги, которое ей нужно, чтобы завершить презентацию подарка в виде сюрприза 3 фута × 4 фута × 5 футов:
SA = (2 × 3 × 4) + (2 × 4 × 5) + (2 × 3 × 5) = 94 фута 2
Капсула
Площадь поверхности капсулы можно определить путем объединения уравнения площади поверхности шара и площади боковой поверхности цилиндра. Обратите внимание, что площадь поверхности оснований цилиндра не включена, поскольку она не составляет часть площади поверхности капсулы. Общая площадь поверхности рассчитывается следующим образом:
СА = 4πr 2 + 2πrh
где r радиус и h высота
Горацио производит плацебо, предназначенное для оттачивания индивидуальности, критического мышления и способности объективно и логически подходить к различным ситуациям.
Он уже протестировал рынок и обнаружил, что подавляющее большинство выборочной совокупности не обладает ни одним из этих качеств и очень готово купить его продукт, еще больше укоренившись в чертах, от которых они так отчаянно стремятся избавиться. Горацио нужно определить площадь поверхности каждой капсулы, чтобы он мог покрыть их чрезмерным слоем сахара и обратиться к предрасположенным к сахару языкам населения, готовясь к своему следующему плацебо, которое «излечивает» все формы сахарного диабета. Учитывая, что в каждой капсуле R из 0,05 дюйма и ч из 0,5 дюйма:
SA = 4π × 0,05 2 + 2π × 0,05 × 0,5 = 0,188 в 2
Spherical Cap
11119. в зависимости от высоты рассматриваемого сегмента. Предоставленный калькулятор предполагает твердую сферу и включает основание колпачка в расчет площади поверхности, где общая площадь поверхности представляет собой сумму площади основания и площади боковой поверхности сферического колпачка.
Если вы используете этот калькулятор для вычисления площади поверхности полой сферы, вычтите площадь поверхности основания. Имея два значения высоты, радиуса крышки или радиуса основания, третье значение можно рассчитать с помощью уравнений, приведенных в калькуляторе объема. Уравнения площади поверхности следующие: сферический колпачок SA = 2πRh
основание SA = πr 2
Общая твердая сфера SA = 2πRh + πr 2
где R — радиус сферической крышки, r — радиус основания, h — высота
Дженнифер завидует глобусу, который ее старший брат Лоуренс получил на день рождения. Поскольку Дженнифер на две трети младше своего брата, она решает, что заслуживает одну треть земного шара своего брата. Вернув ручную пилу отца в сарай для инструментов, она вычисляет площадь поверхности своей полой части земного шара с помощью 9.0218 R 0,80 фута и h 0,53 фута, как показано ниже:
SA = 2π × 0,80 × 0,53 = 2,664 фута площадей его двух круглых концов и площади его боковой поверхности:
круглый конец SA = π(R 2 + r 2 )
боковой SA = π(R+r)√(R-r) 2 + h 2
общая SA = π(R 2 + r 2 ) + π(R+r)√(R-r) 2 + h 2
где R и r — радиусы концов, h — высота
Пол делает вулкан в форме усеченного конуса для своего проекта научной ярмарки.
Пол рассматривает извержения вулканов как насильственное явление и, выступая против всех форм насилия, решает сделать свой вулкан в виде замкнутого конического усеченного конуса, который не извергается. Хотя его вулкан вряд ли произведет впечатление на судей научной выставки, Пол все же должен определить площадь поверхности материала, который ему нужен, чтобы покрыть внешнюю стену своего вулкана R 1 фут, r 0,3 фута и h 1,5 фута:
всего SA = π(1 2 + 0,3 2 ) + π(1 + 0,3) √ 0,3) 2 + 1,5 2 = 10,185 футов 2
Эллипсоид
Вычисление площади поверхности эллипсоида не имеет простой и точной формулы, такой как куб или другая более простая форма. Калькулятор выше использует приблизительную формулу, которая предполагает почти сферический эллипсоид:
SA ≈ 4π 1,6 √(а 1,6 б 1,6 + а 1,6 в 1,6 + б 1,6 906 1 9 ) 30 906 15 1,6 906 1 9 1 9021 где a , b и c — оси эллипса
Колтейн всегда любила готовить и недавно выиграла на конкурсе керамический нож.
К несчастью для его семьи, которая питается почти исключительно мясом, Колтейн практиковал свою технику нарезки на чрезмерном количестве овощей. Вместо того чтобы есть овощи, отец Колтейна уныло смотрит на свою тарелку и оценивает площадь поверхности эллиптических надрезов кабачка с осями 0,1, 0,2 и 0,35 дюйма:
SA ≈ 4π 1.6 √(0.1 1.6 0.2 1.6 + 0.1 1.6 0.35 1.6 + 0.2 1.6 0.35 1.6 )/3 = 0.562 in 2
Square Pyramid
Площадь поверхности квадратной пирамиды состоит из площади ее квадратного основания и площади каждой из четырех треугольных граней. Учитывая высоту 90 218 h 90 219 и длину ребра 90 218 a 90 219 , площадь поверхности можно рассчитать с помощью следующих уравнений:
база SA = a 2
боковой SA = 2a√(a/2) 2 + h 2
всего SA = a 2 + 2a√(a/2) 2 + h 2
В классе Вонкуейлы недавно завершилось строительство модели Великой пирамиды Гизы.
Однако она считает, что модель не излучает ощущение архитектурного чуда, как оригинал, и решает, что покрытие ее «снегом» по крайней мере придаст элемент чуда. Она вычисляет площадь поверхности расплавленного сахара, которая ей потребуется, чтобы полностью покрыть пирамиду с длиной ребра 9.0218 a 3 фута и высота h 5 футов:
всего SA = 3 2 + 2 × 3√(3/2) 2 + 5 2 = 40,321 фута 2
В отличие от Великой пирамиды в Гизе, которая простояла тысячи лет, ее модель, сделанный из крекеров Грэм и покрытый сахаром, продержался всего несколько дней.
Единицы измерения общей площади
Калькулятор веса трубы – британские и метрические единицы
| Калькулятор веса трубы – имперские и метрические единицы |
Калькулятор веса трубы – британские и метрические единицы Нажмите, чтобы просмотреть данные или таблицу:
Формула веса трубы.
Имперская формула:
* В качестве оценки веса следует использовать итоговые значения.
* Для оценки веса следует использовать итоговые значения. | ||||||||||||||||||
Эту формулу можно использовать для определения веса на фут трубы любого размера с любой толщиной стенки.