Удельные потери давления на трение в воздуховодах: 4. Потери давления в системах вентиляции

4. Потери давления в системах вентиляции

1 Потери давления на трение

– коэффициент сопротивления трения. Зависит от режима движения жидкости по воздуховоду.

– кинематическая вязкость, зависит от температуры.

При ламинарном режиме:

при турбулентном движении зависит от шероховатости поверхности трубы. Применяются различные формулы и широко известна формула Альтшуля:

– абсолютная эквивалентная шероховатость материала внутренней поверхности воздуховода, мм.

Для листовой стали 0,1мм; силикатобетонные плиты 1,5 мм; кирпич 4 мм, штукатурка по сетке 10 мм

Удельные потери давления

В инженерных расчетах пользуются специальными таблицами, в которых приводят значения для круглого воздуховода. Для воздуховодов из других материалов вводится поправочный коэффициент и

.

Значение поправочного коэффициента приводится к справочнике в зависимости от вида материала и от скорости перемещения воздуха по воздуховоду.

Для прямоугольных воздуховодов за расчетную величину d принимают эквивалентныйdэк, при которой потери давления в круглом воздуховоде при той же скорости будут равны потерям давления в прямоугольном воздуховоде:

– стороны прямоугольного воздуховода.

Следует иметь в виду: расход воздуха прямоугольного и круглого воздуховодов с при равенстве скоростей не совпадает.

2 Потери давления на местные сопротивления

Местным сопротивлением называют аэродинамическое сопротивление, сосредоточенное в одном месте на коротком участке воздуховода (тройник, поворот, изменение сечения, воздухораспределитель, запорно-регулирующая арматура).

В местных сопротивлениях всегда происходит перестройка полей скоростей и образование на границах потоков вихрей.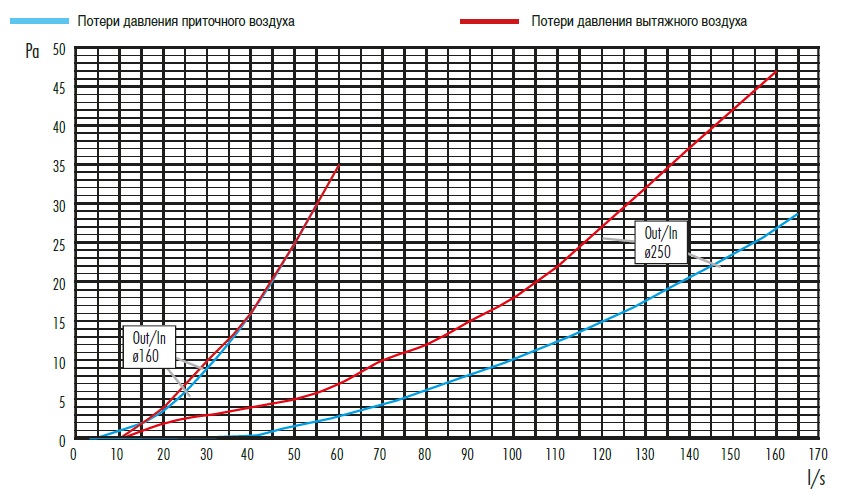

На поддержание вращения вихрей требуются затраты энергии, следовательно прохождении местного сопротивления сопровождается потерей давления. Завихрения начинаются на некотором расстоянии от местных сопротивлений и выравнивается на некотором расстоянии после местного сопротивления (2-3 калибра). На всем этом участке происходят потери давления на трение, но условно для удобства расчета потери давления на местных сопротивлениях считаются сосредоточенными (в одном месте).

Аналитически определяют потери давления на местные сопротивления для некоторых отдельных случаев. Чаще пользуются экспериментальными данными. Потери давления пропорциональны динамическому давлению воздуха в воздуховоде.

.

– коэффициент местного сопротивления, безразмерная величина.

– доля потерь давления в данном сопротивлении отнесенная к динамическому давлению.

Определяют потери давления в долях от динамического давления. Значения принимаются в широких пределах.

При небольших скоростях значения м.б. порядка нескольких десятков или сотен.

Иногда в ответвлении тройников знак имеет отрицательное значение: увеличение удельной энергии потока в ответвлении вследствие инжекции его основным потоком. В расчетах знак нужно учитывать. относится к участку с меньшим расходом.

При движении воздуха с потери давления следует определять с поправочным коэффициентом: – на трение, – на местные сопротивления.

,

При .

При .

3 Распределение давления в системах вентиляции

1. В оздуховод всасывающий

2. Вентилятор.

3. Воздуховод нагнетательный.

4. Линия полного давления со стороны всасывания.

5. Линия статического давления со стороны всасывания.

6. Линия полного давления со стороны нагнетания.

7. Линия статического давления со стороны нагнетания.

О режиме движения воздуха в стальных воздуховодах | C.O.K. archive | 2006

Это можно сделать по таблице 22.15 [1] или по номограмме (рис. 1), составленной по данным этой таблицы. Тем не менее, может потребоваться вычисление удельных потерь для промежуточных скоростей. Для этого требуется интерполяция таблицы. Вообще говоря, ее шаг по скорости достаточно мелкий, в среднем 0,5 м/с, а на при ν< 2 м/с даже ниже. Однако если расчет проводится с применением ЭВМ, например, с использованием электронных таблиц Excel, что очень удобно, т.к. аэродинамический расчет воздуховодов всегда записывается в табличной форме, целесообразно иметь простую и в то же время достаточно точную формулу для R. Нетрудно видеть, что изображенная в логарифмических координатах номограмма представляет собой набор прямых линий. Это означает, что величина R должна находиться в степенной зависимости от параметров ν и d. Таблица хорошо аппроксимируется формулой (1), дающей для наиболее употребительного в общественных зданиях диапазона скоростей 3–6 м/с и диаметров в пределах 315–800 мм погрешность не более 1–2%, а при крайних значениях данных параметров — не более 4–5%, что также заведомо находится в области обычной погрешности инженерных расчетов: R = 0,195 ν ^1,8/(0,01d)^1,2 Па/м. (1) Учитывая, что кинематическая вязкость воздуха при стандартной температуре +20°С составляет ν= 1,51 •10^–5 м²/с [2], выражение (1) легко привести их к критериальному виду: λ= 0,1888/Re ^0,2, (2) где Re = ν d/n — безразмерный критерий Рейнольдса, при вычислении которого величина d подставляется в метрах; λ— опять-таки безразмерный коэффициент гидравлического трения [2], численно равный потерям на трение, выраженным в долях динамического давления Р_д = ρν²/2, на участке воздуховода с длиной, совпадающей с диаметром. Здесь ρ— плотность воздуха, равная при стандартных условиях 1,2 кг/м³ [2]. В соотношение (2) в явном виде не входит шероховатость стенок. Это заставляет считать, что стальные воздуховоды при обычных диаметрах и скоростях воздуха являются гидравлически гладкими. Иначе говоря, хотя в [1] и указано конкретное значение абсолютной эквивалентной шероховатости k_э = 0,1 мм, практически никакой роли в аэродинамическом сопротивлении она не играет. В то же время числа Рейнольдса при этом могут быть значительными, например, для ν= 6 м/с и d = 0,5 м получаем Re = 2•10⁵. Однако это лежит за пределами применимости известной формулы Блазиуса для гладких труб [2] (Re < 10⁵): λ= 0,3164/Re_0,25. (3) Собственно говоря, вид выражения (2) при сравнении с (3) показывает, что зависимость коэффициента трения от числа Re для стальных воздуховодов более слабая, чем по Блазиусу, поскольку степень при величине Re меньше. На рис. 2 приведены графики изменения λ в рассматриваемом диапазоне Re по Блазиусу (черная линия), по более точной формуле Прандтля-Никурадзе [2], пригодной, в отличие от (3), для всей области движения в гладких трубах (серая линия), и по соотношению (2) — пурпурная линия. Формула ПрандтляНикурадзе обычно записывается в следующем виде: 1/ λ ^0,5 = 2lg(Re λ ^0,5)– 0,8. (4) Видно, что с ростом числа Рейнольдса расхождение между значениями, получаемыми по выражениям (2) и (3), постепенно возрастает и достигает 12%. Такого же порядка будет погрешность, если использовать универсальную формулу Альтшуля [1]: λ= 0,11(k_э/d + 68/Re)^0,25. (5) Заметим, что выражение (5) в явном виде содержит величину эквивалентной шероховатости. Однако, как показано в [3], при Re(k_э/d)< 10 имеет место область гидравлической гладкости. Легко вычислить, что для стальных воздуховодов это будет наблюдаться при ν< 1,5 м/с, но и при скоростях порядка 5–7 м/с, характерных для систем механической вентиляции, данное соотношение оказываетсяв пределах всего 35–45, что отличается от граничного значения, равного 10, менее, чем на порядок, поэтому фактически влияние шероховатости не выходит за пределы точности инженерного расчета. В таких же пределах находится и погрешность самой таблицы 22. 15 [1]. В то же время линии, соответствующие формулам (2) и (4), идут практически на одинаковом расстоянии. Это означает, что соотношение (2) правильно описывает режим движения воздуха в стальных воздуховодах для рассматриваемой области скоростей и диаметров. Небольшое постоянное превышение (порядка 5%) даваемых ею значений λ объясняется, по-видимому, введенным в таблицу 22.15 [1] запасом на влияние стыков и других местных особенностей. В то же время формулы (2) и тем более (1), из которой она была получена, очень просты, наглядны и легко доступны для инженерных расчетов, особенно при использовании электронных таблиц Excel, а также в учебном процессе.Их применение позволяет отказаться от интерполяции таблиц при сохранении точности, требуемой для инженерных расчетов, и непосредственно вычислять удельное сопротивление воздуховодов при любых диаметрах и скоростях воздуха в пределах 1–8 м/с. Этого вполне достаточно для жилых, общественных и большинства промышленных зданий.

---

1. Справочник проектировщика. Внутренние санитарно-технические устройства. Ч. 3. Вентиляция и кондиционирование воздуха. Кн. 2. Под. ред. Н.Н. Павлова и Ю.И. Шиллера.— М.: ≪Стройиздат≫, 1992. 2. Теория тепломассообмена. Под. ред. А.И.Леонтьева.— М.: Изд-во МГТУ им.Н.Э. Баумана, 1997. 3. Альтшуль А.Д., Животовский Л.С., Иванов Л.П. Гидравлика и аэродинамика.— М.: ≪Стройиздат≫, 1987.

Как рассчитать потери давления в воздуховоде — BIM4Tips

24 декабря 2019 г. Брайан Джонсон в руководствах по проектированию, учебных пособиях, строительных стандартах

ОБНОВЛЕНО: 29.10.2022

В гидродинамике уравнение Дарси–Вейсбаха представляет собой эмпирическое уравнение, которое связывает потерю напора или потери давления из-за трения на заданной длине трубы со средней скоростью поток жидкости для

несжимаемой жидкости . Для получения дополнительной информации о сжимаемых и несжимаемых жидкостях см. «Как спроектировать систему сжатого воздуха».

Уравнение Дарси-Вейсбаха

ρ , плотность жидкости.
D , гидравлический диаметр воздуховода D = 2 a b / (a ​​+ b).
⟨v⟩ , средняя скорость потока, экспериментально измеренная как объемный расход Q на единицу смоченной площади поперечного сечения.
fD , коэффициент трения Дарси (также называемый коэффициентом текучести λ).

Ниже Уравнение Свами-Джейна , используемое для прямого решения коэффициента трения Дарси-Вейсбаха f полнопроточной круглой трубы. Это уравнение является аппроксимацией неявного

уравнения Коулбрука-Уайта , где число Рейнольдса Re > 4000 и имеет турбулентный поток. Где ламинарный поток имеет Re < 2100, а переходный поток 2100 < Re < 4000 (рис. 1).

Рис. 1: Диаграмма профиля скорости.

Уравнение Коулбрука-Уайта

Уравнение Свами-Джейна

Номер Рейнольдса

Относительная шероховатость трубы ε / D , где ε — эффективная высота шероховатости трубы, а

D — диаметр трубы (внутренний).

u , скорость жидкости относительно объекта.
L , является характерным линейным размером.
μ — динамическая вязкость жидкости.
ν — кинематическая вязкость жидкости.

У нас есть оцинкованный воздуховод размером 24 x 12 дюймов, подающий воздух при 55°F/60% относительной влажности (ОВ) с расходом 1700 кубических футов в минуту и ​​длиной 100’-0”. Какова потеря давления в воздуховоде? 92) = 14.1666 ft/sec
Galvanized Pipe Roughness ε = 0.0003 ft (see below Revit Type Properties)
Relative roughness ε / D = 0.0003 ft / 1.3333 ft =

0.00025006
Velocity of the жидкости относительно объекта u = 14,1666 фут/сек
Характеристический линейный размер цилиндра L = 1,3333 фут
Динамическая вязкость μ = c = 9009, 9002, 1 0,0000134394 фунт/фут-сек

РИСУНОК 2 Психометрические данные при 55Fdb/60%RH с использованием программного обеспечения Cook Psychometric. Узнайте больше об этом программном обеспечении в компании Loren Cook http://www. lorencook.com/downloads.asp.

РИСУНОК 3. Типовые свойства Revit для примера прямоугольного воздуховода.

92)
ΔP/L = 0,000023 PSI
ΔP/L 0,000023 PSI (27,7076 дюйм вод. ст. / PSI)
Δp / L = 0,00064 в WG

С. Потеря трения составляет Δp = 0,064 в WG / 100 футов

Проверьте свой ответ:

. потеря ΔP = 0,063 дюймов водяного столба / 100 футов

РИСУНОК 4 Проверка расчета с помощью Revit.

Список ссылок:

• En. wikipedia.org. (2019). Уравнение Дарси–Вейсбаха. [онлайн] Доступно по адресу: https://en.wikipedia.org/wiki/Darcy%E2%80%93Weisbach_equation [По состоянию на 18 сентября 2019 г.].

• Autodesk.com. (2019). Ревит | Программное обеспечение BIM | Автодеск. [онлайн] Доступно по адресу: https://www.autodesk.com/products/revit/overview [По состоянию на 18 сентября 2019 г.].

24 декабря 2019 г. / Брайан Джонсон

Размеры воздуховодов, воздуховоды, давление, скорость, учебные пособия

Руководства по проектированию, учебные пособия, строительные стандарты

Влияние сжатия на потерю давления в гибких воздуховодах ОВиК (Журнальная статья)

Влияние сжатия на потерю давления в гибких воздуховодах ОВКВ (Журнальная статья) | ОСТИ.GOV

перейти к основному содержанию

• Полная запись
• Другие родственные исследования

Было проведено исследование для оценки влияния сжатия на перепад давления в гибких воздуховодах со спиральной проволочной спиралью, используемых в жилых и коммерческих помещениях.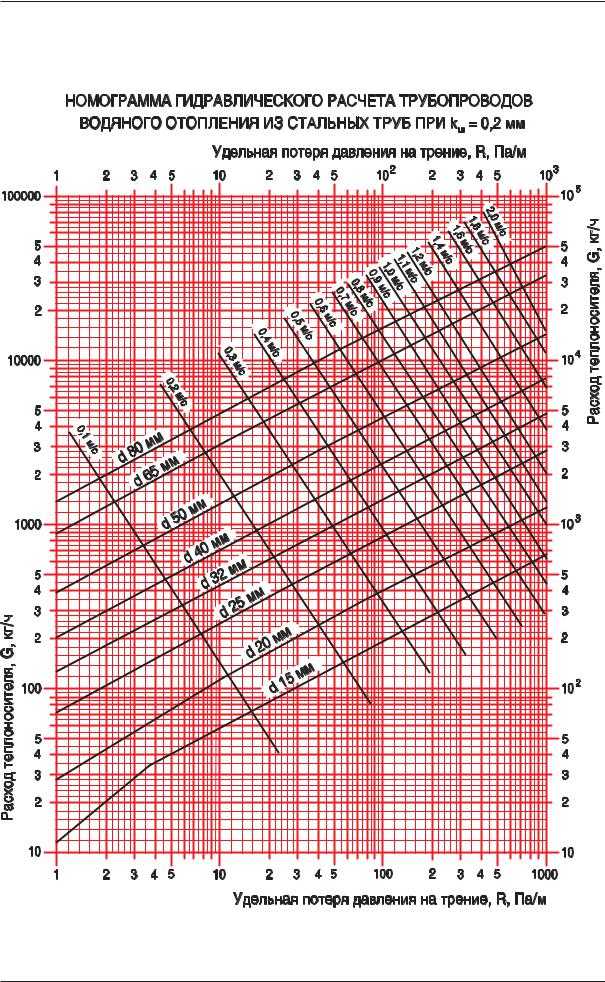 Воздуховоды с номинальным диаметром 6 дюймов, 8 дюймов и 10 дюймов (150, 200 и 250 мм) были испытаны при различных конфигурациях сжатия в соответствии со стандартом ASHRAE 120-19.99 — Методы испытаний для определения гидравлического сопротивления воздуховодов и фитингов ОВКВ. Результаты показали, что доступные опубликованные ссылки имеют тенденцию недооценивать эффекты сжатия. Исследование показало, что умеренное сжатие в гибких воздуховодах, типичное для полевых установок, может увеличить падение давления в четыре раза, а дальнейшее сжатие может увеличить падение давления почти в десять раз. Результаты показали, что поправочный коэффициент падения давления для сжатых воздуховодов не может быть независимым от размера воздуховода, как это было предложено ASHRAE Fundamentals, и поэтому было разработано новое соотношение для более точного количественного определения падения давления в гибких воздуховодах. Это исследование также предлагает потенциальные улучшения стандарта ASHRAE 120-19.99 и предоставляет новые данные для проектирования воздуховодов.

Авторов:

Абушакра, бас; Уокер, Иэн С; Шерман, Макс Х.

Дата публикации:

01.07.2002

Исследовательская организация:

Национальная лаборатория Лоуренса в Беркли. (LBNL), Беркли, Калифорния (США)

Организация-спонсор:

Директор Министерства энергетики США. Помощник госсекретаря по энергоэффективности и возобновляемым источникам энергии. Офис программы строительных технологий. Государственные и общественные программы. Управление строительных исследований и стандартов; Тихоокеанская газовая и электрическая компания. Калифорнийский институт энергоэффективности, контракт S9902А (США)

Идентификатор ОСТИ:

836654

Номер(а) отчета:

LBNL-49012
Проект НИОКР: 884406; РНН: US200504%%246

Номер контракта Министерства энергетики:  

AC03-76SF00098

Тип ресурса:

Журнальная статья

Название журнала:

Исследования HVAC и R

Дополнительная информация журнала:

Объем журнала: 10; Выпуск журнала: 3; Дополнительная информация: Представлено в HVac and R Research: Volume 10, No. 3; Дата публикации в журнале: 07/2004; PBD: 1 июля 2002 г.

Страна публикации:

США

Язык:

Английский

Тема:

32 ЭНЕРГОСБЕРЕЖЕНИЕ, ПОТРЕБЛЕНИЕ И ИСПОЛЬЗОВАНИЕ ЭНЕРГИИ; СЖАТИЕ; ДИЗАЙН; ВОЗДУХОВОДЫ; ПАДЕНИЕ ДАВЛЕНИЯ; ТЕСТИРОВАНИЕ

---

Форматы цитирования

• ВПП
• АПА
• Чикаго
• БибТекс

Abushakra, Bass, Walker, Iain S, and Sherman, Max H. Влияние сжатия на потерю давления в гибких воздуховодах ОВКВ . США: Н. П., 2002. Веб.

Копировать в буфер обмена

Абушакра, Басс, Уокер, Иэн С. и Шерман, Макс Х. Влияние сжатия на потерю давления в гибких воздуховодах ОВКВ . Соединенные Штаты.

Копировать в буфер обмена

Абушакра, Басс, Уокер, Иэн С. и Шерман, Макс Х. 2002. «Влияние сжатия на потерю давления в гибких воздуховодах ОВКВ». Соединенные Штаты. https://www.osti.gov/servlets/purl/836654.

Копировать в буфер обмена

@статья{osti_836654,
title = {Влияние сжатия на потерю давления в гибких воздуховодах ОВиК},
автор = {Абушакра, Басс и Уокер, Иэн С. и Шерман, Макс Х.},
abstractNote = {Исследование было проведено для оценки влияния сжатия на падение давления в гибких воздуховодах со спиральной проволочной спиралью, используемых в жилых и коммерческих помещениях. Воздуховоды с номинальным диаметром 6 дюймов, 8 дюймов и 10 дюймов (150, 200 и 250 мм) были испытаны при различных конфигурациях сжатия в соответствии со стандартом ASHRAE 120-19. 99 -- Методы испытаний для определения гидравлического сопротивления воздуховодов и фитингов ОВКВ. Результаты показали, что доступные опубликованные ссылки имеют тенденцию недооценивать эффекты сжатия. Исследование показало, что умеренное сжатие в гибких воздуховодах, типичное для полевых установок, может увеличить падение давления в четыре раза, а дальнейшее сжатие может увеличить падение давления почти в десять раз. Результаты показали, что поправочный коэффициент падения давления для сжатых воздуховодов не может быть независимым от размера воздуховода, как это было предложено ASHRAE Fundamentals, и поэтому было разработано новое соотношение для более точного количественного определения падения давления в гибких воздуховодах. Это исследование также предлагает потенциальные улучшения стандарта ASHRAE 120-19.99 и предоставляет новые данные для проектирования воздуховодов.},
дои = {},
URL = {https://www.osti.gov/biblio/836654}, журнал = {HVac & R Research},
номер = 3,
объем = 10,
место = {США},
год = {2002},
месяц = ​​{7}
}

Копировать в буфер обмена

---

Просмотреть журнальную статью (0,54 МБ)

Найти в Google Scholar

Поиск в WorldCat, чтобы найти библиотеки, в которых может храниться этот журнал Вы должны войти в систему или создать учетную запись, чтобы сохранять документы в своей библиотеке.