Удельные потери давления на трение в воздуховодах – Потери давления на трение в стальных воздуховодах

Определение удельной потери давления в воздуховодах — Студопедия.Нет

Цель работы: Определение удельной потери давления опытным путём для круглого стального воздуховода при различных скоростях движения воздуха и сравнение полученных данных с табличными.

Общие указания

Потери давления на трение возникают по всей длине воздуховода и при данных геометрических размерах и расходе зависят от режима течения и состояния поверхности трения. Потери давления на трение в общем виде можно определить по формуле:

                                                               (3.1)

где: DР_тр – потери давления на трение, Па;

l – коэффициент трения;

l – длина воздуховода, м;

R_г – гидравлический радиус поперечного сечения воздуховода (отношение площади поперечного сечения к периметру), м;

Р_д – динамическое давление потока, Па.

Для наиболее распространённого круглого поперечного сечения воздуховода:

D = 4×R_г,     тогда                            (3.2) (3.3)

Для квадратного и наиболее распространённого прямоугольного поперечного сечения размером a´b имеем:

                                                                  (3.4)

откуда при условии равенства скоростей получаем значение эквивалентного диаметра по скорости:

                                                                         (3.5)

Если скорости представить в виде расходов, делённых на площади поперечных сечений, то при условии равенства расходов (а также R_г) получим значение диаметра, эквивалентного по расходу:

                                                            (3.6)

При расчете прямоугольных воздуховодов обычно пользуются значениями эквивалентных диаметров более простого вида

d_эv.

Для точного расчета потерь давления на трение необходимо правильно определять сложный по своей природе коэффициент трения l, в общем случае зависящий от состояния стенок (относительной шероховатости k/d и режима течения, определяемого величиной критерия Рейнольдса Re).

Коэффициент трения является переменной величиной и при ламинарном режиме движения воздуха зависит от числа Re. При турбулентном режиме движения, кроме числа Re, коэффициент трения зависит также и от коэффициента относительной шероховатости k/d. Коэффициент трения при ламинарном режиме движения воздуха определяется по формуле Пуазейля. При турбулентном режиме один и тот же воздуховод при данной его шероховатости, характеризуемой отношением

k/d, в зависимости от числа Re может быть гидравлически гладким или гидравлически шероховатым. Переходным критерием является величина 67,5×(k/d). Воздуховод считается гидравлически гладким при Re <67,5×(k/d) и в этом случае коэффициент трения вычисляется по формуле Блазиуса:

                                                                          (3.7)

При Re >67,5×(k/d) воздуховоды считаются гидравлически шероховатыми и l находится по формуле Шифринсона:

                                                                 (3.8)

Порядок выполнения работы

Работа выполняется на участке А всасывающего воздуховода лабораторной установки, представленной на рисунке 3.1.

На участке А имеется два штуцера для установки в воздуховод пневмометрических трубок. При движении воздуха по воздуховоду в направлении, указанном стрелкой, вследствие потерь давления на трение полное давление в сечении II будет меньше полного давления в сечении I на величину потерь на трение DР.

Следовательно,

DР = Р_I – Р_II.                                                                         (3.9)

Потеря давления DР, отнесённая к 1 погонному метру длины воздуховода, будет искомой величиной удельного сопротивления трению R. Таким образом, измерив при помощи пневмометрических трубок и микроманометра величину полного давления в сечениях I и II, можно определить удельную потерю давления R как частное от деления разности полных давлений на длину воздуховода между сечениями I и II:

R = (Р_I – Р_II)/l.                                                                     (3.10)

Рис. 3.1 Схема установки для определения удельной потери давления

В работе величину R определяют для 4¸5 значений расхода воздуха. Расход воздуха изменяется при помощи шибера. Для нахождения расхода воздуха в одном из сечений измеряется также и динамическое давление, по величине которого подсчитывается скорость движения воздуха по воздуховоду:

                                                                        (3.11)

где: v_ср – скорость движения воздуха, м/с;

r – плотность воздуха при температуре помещения, кг/м³;

Р_д – динамическое давление, Па.

Данные измерений и результаты расчетов заносят в таблицу 3.1.

Таблица 3.1 – Результаты измерений и расчетов по определению удельной потери давления на трение

Номер опыта	Размеры воздуховода		l, м	PI, Па	PII, Па	Pд, Па	R, Па/м	v, м/с	L, м3/с	Re	l	Rт, Па/м
	d, м	F, м2
1	2	3	4	5	6	7	8	9	10	11	12	13
1
2
…

По полученным результатам выполнить следующее:

1. Сравнить полученную из опытов величину R с теоретической R_т (по справочным данным).

2. Определить режим движения воздуха в вохдуховоде.

3. Построить график зависимости R = f(L).

Лабораторная работа 4

studopedia.net

Аэродинамический расчет вентиляции

ТОП 10:

Аэродинамический расчёт сети производится с целью определения суммарного давления, необходимого для обеспечения расчётного расхода воздуха по всем участкам и необходимого сечения воздуховодов. Суммарная потеря давления, Р, Па, определяется как сумма потерь давления на трение и местные сопротивления. (37) где R – потери давления на трение на 1 м длины воздуховода, Па/м; l – длина расчётного участка, м; Z – потери давления на местные сопротивления на расчётном участке. Потери давления на 1 м длины воздуховода определяются по формуле: (38) где – потери давления на трение на 1 м длины воздуховода, Па/м; d – диаметр воздуховода расчётного участка, м; – скоростное (динамическое) давление, Па. Потери на местные сопротивления определяются по формуле: (39) где – сумма коэффициентов местных сопротивлений на расчётном участке. Скорость движения воздуха в жалюзийных решётках определяем по формуле: (40) где L – количество воздуха, м³/ч; n – количество жалюзийных решёток; – площадь сечения жалюзийных решёток, м². По этим формулам составлена расчётная таблица. По допустимым скоростям воздуха в воздуховодах до 8 м/с и расходу подбираем размер воздуховода d и находим потери давления на трение R Па/м и динамическое давление , Па. Результаты аэродинамического расчёта приточной и вытяжной вентиляции сводим в таблицу 6.   Таблица 6.1 -Аэродинамический расчет воздуховодов П1     № уч. Расчет воздуховода L, м3/ч Длина L, м Размер воздуховода а х б, мм Скорость воздуха, υ, м/с Эквива-лентный d, мм Удельные потери давления R, Па/м Коэф. шерохова-тости n Потери на трениеRℓn, Па Σξ Динами-ческое давление, Рg, Па Потери на местные сопро-тивлениях Z, Па Rℓn+ Z, Па Расчет концевых участков 7,1 200х100 2,5 0,81 1,28 7,4 0,16 4,0 12,0 300х100 2,65 0,75 1,28 1,9 0,34 4,2 4,54 200х100 0,59 1,25 1,5 0,46 1,8 2,26 0,5 200х100 2,7 0,90 1,29 0,6 0,25 4,4 4,65 300х100 2,6 0,03 1,29 0,1 0,84 0,3 0,84 600х200 4,2 0,72 1,38 0,36 10,6 10,96 600х200 4,2 0,72 1,38 0,24 10,6 10,84 2,6 200х100 0,01 1,29 0,1 0,16 0,02 0,19 200х100 2,5 0,81 1,27 7,2 0,28 4,0 4,28 300х100 2,7 1,84 1,3 4,8 0,45 9,7 9,45 0,5 200х100 0,01 1,25 0,1 0,26 0,26 0,52 200х100 0,11 1,25 0,4 0,48 0,4 0,88                                                           Расчет магистральных участков 7,1 200х100 2,5 0,81 1,28 7,4 0,35 4,0 1,4 300х100 4,3 1,84 1,39 0,4 11,5 4,6 1,4 300х100 4,9 2,31 1,4 4,5 0,4 14,7 5,9 6,7 400х200 2,5 0,33 1,29 2,9 0,7 3,9 2,7 600х200 6,5 1,62 1,45 21,1 0,52 25,6 13,3 1,9 600х350 6,1 0,89 1,44 2,4 0,57 22,6 12,9 1,9 600х350 6,1 0,89 1,44 2,4 0,57 22,7 12,9 700х400 5,1 0,54 1,41 6,1 - 15,3 15,3 16,44 7,2 700х400 5,1 0,54 1,41 3,8 0,45 9,79 177+4,4= 181,4 182,66                                                   ∑1141,8* 1,1=1256                               Таблица 6.2-Аэродинамический расчет воздуховодов П2     № уч. Расчет воздуховода L, м3/ч Длина L, м Размер воздуховода а х б, мм Скорость воздуха, υ, м/с Эквива-лентный d, мм Удельные потери давления R, Па/м Коэф. шерохова-тости n Потери на трениеRℓn, Па Σξ Динами-ческое давление, Рg, Па Потери на местные сопро-тивлениях Z, Па Rℓn+ Z, Па     6,8 200х100 2,6 0,81 1,29 7,1 0,38 4,0 1,5 200х100 2,8 0,92 1,31 2,4 0,38 4,5 1,7 200х100 0,9 0,12 1,14 0,4 0,32 0,5 0,1 200х100 2,0 0,51 1,25 1,3 0,36 2,4 0,9 3,5 200х100 1,5 0,32 1,21 1,3 0,35 1,4 0,5 0,5 200х100 2,9 1,02 1,31 0,7 0,38 5,1 1,9 200х100 3,0 1,10 1,32 2,9 0,38 5,5 2,1 3,5 200х100 2,3 0,69 1,27 3,0 0,33 3,3 1,1 3,5 400х200 3,5 0,59 1,34 2,8 0,42 7,2 3,0 3,5 400х200 3,5 0,59 1,34 2,8 0,42 7,2 3,0 0,5 200х100 2,9 1,02 1,31 0,7 0,38 5,1 1,9 500х250 5,1 1,09 1,41 3,1 0,47 15,6 7,3 0,5 200х100 0,4 0,03 1,08 0,0 0,31 0,1 0,0 200х100 2,8 0,95 1,31 2,5 0,38 4,7 1,8 8,5 200х100 2,9 1,01 1,31 11,2 0,38 5,0 1,9                                                     Расчет магистральных воздуховодов   8,6 200х100 2,6 0,81 1,29 0,31 1,2 4,1 200х100 6,2 4,04 1,45 0,84 23,0 19,3 2,5 300х100 2,7 0,43 1,3 1,4 0,35 4,5 1,6 300х100 3,2 0,59 1,33 0,8 1,28 6,3 8,0 300х100 4,2 0,95 1,38 2,6 0,45 10,6 4,8 2,3 400х200 3,9 0,73 1,36 2,3 0,74 9,2 6,8 2,6 400х200 4,5 0,94 1,4 3,4 0,36 12,1 4,4 8,4 600х200 5,3 1,10 1,43 13,3 0,87 16,9 14,7 2,4 600х200 5,3 1,10 1,43 3,8 0,24 16,9 4,1 3,2 600х350 4,6 0,53 1,4 2,4 0,31 12,9 4,0 7,2 700х400 5,7 0,66 1,43 6,7 1,2 19,7 19,7 6,5 700х400 5,7 0,66 1,43 6,1 0,45 19,7 186,3+8,9=195,2   ∑1259,8* 1,1=1315     Таблица 6.3-Аэродинамический расчет воздуховодов В1     № уч. Расчет воздуховода L, м3/ч Длина L, м Размер воздуховода а х б, мм Скорость воздуха, υ, м/с Эквива-лентный d, мм Удельные потери давления R, Па/м Коэф. шерохова-тости n Потери на трениеRℓn, Па Σξ Динами-ческое давление, Рg, Па Потери на местные сопро-тивлениях Z, Па Rℓn+ Z, Па Расчет концевых участков 200х100 2,9 1,01 1,32 9,3 1,24 5,0 6,2 3,8 200х100 2,6 0,05 1,29 0,3 0,86 2,4 2,4 9,6 400х200 4,1 0,81 1,37 9,6 0,31 10,2 3,2 7,5 200х100 1,8 0,14 1,24 1,3 1,12 0,6 1,3 5,2 200х100 1,7 0,09 1,23 0,5 0,45 0,3 2,2 200х100 2,6 0,06 1,29 0,2 0,34 0,2 3,6 6,8 200х100 3,7 1,58 1,35 14,5 0,28 8,3 2,3 Расчет магистральных участков 200х100 6,5 4,43 1,45 51,4 1,2 25,5 30,6 7,7 200х100 7,1 5,17 1,47 58,5 0,48 30,1 14,5 2,2 400х200 2,0 0,22 1,25 0,6 0,34 2,4 0,8 400х200 2,1 0,24 1,25 1,2 0,26 2,6 0,7 2,3 600х200 1,8 0,15 1,24 0,4 1,4 1,9 2,6 600х200 1,9 0,17 1,24 0,7 0,31 2,2 0,7 3,7 600х200 4,8 0,90 1,4 4,7 0,27 13,6 3,7 6,4 700х400 2,9 0,18 1,32 1,6 1,01 4,9 4,9 700х400 2,9 0,18 1,32 1,9 0,8 4,9 3,9                         ∑499·1,1 =549                                 Расчет и подбор оборудования 

infopedia.su

Репозиторий БНТУ 0,11 ( ). Лабораторная работа 1 ОПРЕДЕЛЕНИЕ УДЕЛЬНОЙ ПОТЕРИ ДАВЛЕНИЯ НА ТРЕНИЕ В ВОЗДУХОВОДАХ

Транскрипт

1 Лабораторная работа 1 ОПРЕДЕЛЕНИЕ УДЕЛЬНОЙ ПОТЕРИ ДАВЛЕНИЯ НА ТРЕНИЕ В ВОЗДУХОВОДАХ 1. Цель работы Экспериментальное определение величины потерь давления на трение при движении воздуха в металлическом воздуховоде о поперечным сечением круглой формы и сравнение полученной величины с табличными значениями. 2. Теоретические положения При движении воздухе по прямолинейному воздуховоду имеются потери давления на преодоление сил трения о стенки воздуховода. Сопротивление трения, отнесенное к 1 м длины воздуховоде круглого постоянного сечения R, Па, может быть определено из выражения: 2 v R ; (1.1) d 2 где λ коэффициент трения; d диаметр воздуховода, м.; v скорость движения воздуха, м/с; ρ плотность воздуха при данной температуре, кг/м 3. Коэффициент трения является переменной величиной и при ламинарном режиме движения воздуха зависит только от числа Рейнольдса. При турбулентном режиме движения, креме числа Рейнольдса, коэффициент трения зависит также и от так называемого коэффициента k относительной шероховатости ; где k абсолютная шероховатость – высота выступов в d мм на внутренней поверхности воздуха; d диаметр воздуховода, мм. При турбулентном режиме движения воздуха один и тот же воздуховод при данной его шероховатости, характеризуемой отношением, в зависимости от числа Рейнольдса может быть аэродинамически гладким или аэродинамически шероховатым. Воздуховод считается аэродинамически гладким при Re 67,5 d и в этом случае k коэффициент трения вычисляется по формуле Блазиуса: При Re 0,3164 0,25. (1.2) Re 67,5 d воздуховод считается аэродинамически шероховатым, и коэффициент k трения находят по формуле Шифринсона: k d 0,25 0,11 ( ). (1.3) На основании выражения (1.1) для круглых стальных воздуховодов при движении по ним воздуха с t = 20 O C для P o = 101,325 кпа; ϕ =50% составлены таблицы и номограммы, позволяющие определить удельную потерю давления на трение R. В задачу лабораторной работы входит определение R опытным путем для стального воздуховода круглого сечения при различных скоростях движения воздуха и сравнение полученных данных с табличными.

2 3. Экспериментальная установка. Методика проведения эксперимента Работа выполняется на участке I II нагнетательного воздуховода лабораторного аэродинамического стенда, представленного на рис.1.2. На рис.1.2 показана схема присоединения микроманометров к единичным трубкам для измерения на испытываемом участке I II полных и динамического давлений. При движении воздуха по воздуховоду в направлении, указанном стрелкой, вследствие потерь давления на трение полное давление в сечении II II будет меньше полного давления в сечении I I на величину этих потерь P. I II Следовательно, P Pn Pn. (1.4) Потеря давления P и будет искомой величиной R, так как расстояние между сечениями I I и II II равно 1 м. I II P P P. (1.5) n n Рис. 1.1 В работе величину R определяют для 4 5 значений скорости движения воздуха. 2 P Скорость движения воздуха, м/с, определяется по выражению: v o, где Р о динамическое давление, Па, измеренное в одном из сечений (т.к. при d = = const расход и скорость в сечениях данного участка также = const). Для этого присоединяют трубку полного давления (+) к резервуару, а трубку статического давления ( ) к капилляру микроманометра рис.1.2, имея в виду, что Р о = Р n Р c (1.6) Расход и скорость изменяется на стенде путем изменений поперечного сечения воздуховода с помощью шибера (3), при этом шиберы (1,2) находятся в закрытом состоянии. 4. Обработка экспериментальных данных Методика определения средней скорости движения воздуха в воздуховоде приведена в работе 6 (часть 1). Данные измерений и результаты расчетов заносят в таблицу 1.1.

3 опытов d, мм l, м P n II, Па P n I, Па P, Па R, Па/м P o oc, Па v ос, м/с v ср, м/с Таблица 1.1 R таб л, Па/м По данным таблицы отроится график в координатах: средняя скорость и соответствующее динамическое давление – ось абсцисс, дельная потеря давления на трение R ось ординат. На этот же график наносится кривая зависимости R f () v по табличным данным для диаметра d = 100 мм и полученных в работе средних значений скорости. На основании полученных данных проводится анализ экспериментальной и теоретической кривых. Построенный график зависимости R от скорости (динамического давления) будет использоваться при выполнении последующих лабораторных работ. 5. Контрольные вопросы 1. Что такое удельная потеря давления по длине воздуховода и ее размерность? 2. От каких величин зависит значение R? 3. Что следует понимать под терминами относительная и абсолютная шероховатость? 4. Как изменяется величина R в зависимости от скорости движения воздуха? Лабораторная работа 2 ИССЛЕДОВАНИЕ КОЭФФИЦИЕНТОВ МЕСТНЫХ СОПРОТИВЛЕНИЙ ПРИТОЧНОГО ТРОЙНИКА 1. Цель работы Опытным путем определить коэффициенты местных сопротивлений на проход и ответвление приточного тройника под прямым углом и сравнить результаты с данными, приведенными в справочной литературе. 2. Теоретические положения Потери давления в местных сопротивлениях (отводы, тройники, крестовины, внезапные расширения и др.) возникают вследствие вихреобразований при разделении или слиянии потоков. В отводах давление теряется на закручивание воздушного потока и образование двух вихревых зон. В тройниках давление расходуется на вихре- образования при разделении или слиянии потоков. Потери давления в любом местком сопротивлении определяются по формуле: 2 v Z ; (2.1) 2 где ζ коэффициент местного сопротивления; v средняя скорость воздушного потока, м/с. Для большинства подобных местных сопротивлений величины ζ постоянны. Независимость от их числа Re указывает на незначительность вязкого сопротивления (трения) по сравнению о потерями от вихреобразований.

4 В устройствах c очень развитыми поверхностями (пластинчатые калориферы, фильтры и пр.) вязкость (трение) играет заметную роль. В этом случае показатель степени средней скорости является величиной переменной, и изменение потери давления в местном сопротивлении непропорционально квадрату средней скорости движения воздуха в сечении. 3. Экспериментальная установка. Методика проведения опытов Определение коэффициентов местных сопротивлений тройника (на проход ζ пр, ответвление ζ от ), работающего на нагнетание, производится на аэродинамическом стенде, испытываемый тройник которого изображен на рис На рис.2.1 приведены также схемы присоединения единичных трубок для измерения динамических и полных давлений в соответствующих сечениях. Для определения величины ζ пр нужно опытным путем найти значения полных давлений P ср II и P III ср в сечениях II и III и определить динамическое давление P IV д ср в сечении IV. II V По аналогии для нахождения ζ от нужно найти значения полных давлений P n ср и P n ср соответственно в сечениях II и V, а также динамическое давление в сечении VI. Рис. 2.1 Величина коэффициента местного сопротивления определяется по следующим выражениям: II III II III Pn ср Pn ср Pn ср ; (2.2) P P ср IV IV o ср o ср II V II V Pn ср Pnср Pn ср ; (2.3) P P ОТ VI VI o ср o ср

5 Так как в сечениях II,II,V измерить полные давления не представляется возможным из-за близости местного сопротивления (где происходит возмущение потока), измерение полных давлений производится на расстояниях l 1, l 2 и l 3 в сечениях соответственно I, VI и IV. В этих же сечениях измеряются и динамические давления P I д, P VI д и P IV д, которые нужны для определения коэффициентов ζ и используются для нахождения средних, значений скоростей и расходов в стволе, проходе и ответвлении тройника. Для получения значений полных давлений в сечениях II, III и V производится расчет по выражениям: P P R l (2.4) II n ср I n ср 1 1 ; P P R l (2.5) III n ср V n ср IV n ср VI n ср 4 3 ; P P R l (2.6) 6 2 ; I где P n ср, P IV VI n ср, P n ср измеренные полные средние давления в сечениях I, IV, VI; R 1, R 4, R 6 удельные потери давления в воздуховодах при значениях средних динамичеоких давлений, измеренных в сечениях I, IV, VI. Значения R 1, R 4, R 6 берутся из графика, построенного при выполнении лабораторной работы 1. Работа выполняется при различных соотношениях расходов в стволе, проходе и ответвлении, что осуществляется 5-6 раз путем изменения сечений ответвления и прохода шиберами Ш-1 и Ш Обработка опытных данных Результаты измерений и расчетов заносятся в табл.2.1. Таблица 2.1 изм. Pn ср I, Па Pn ср IV, Па Pn ср VI, Па Pо ср I, Па Pо ср IV, Па Po ср VI, Па R1, Па/м R4, Па/м R6, Па Полученные опытным путем значения коэффициентов местных сопротивлений тройника ζ пр и ζ от сравнивают со значениями коэффициентов местных сопротивлений, определяемых по графику рис Контрольные вопросы 1. Чем вызваны местные потери давления в тройниках? 2. Изменение каких параметров в тройниках влияет на величину местных сопротивлений ζ пр и ζ от? 3. В долях какого давления выражены коэффициенты местных сопротивлений? l1, м l2, м l3, м Pn ср II, Па Pn ср V, Па Pn ср III, Па ζпр ζот Примеч.

6 Лабораторная работа 3 АЭРОДИНАМИЧЕСКОЕ ИССЛЕДОВАНИЕ МАТЕРЧАТЫХ ФИЛЬТРОВ ри й υ0 – средняя скорость в ответвлении, м/с; υс – средняя скорость в стволе, м/с; υпр – средняя скорость в проходе, м/с БН ТУ 1.Цель работы Исследование аэродинамического сопротивления матерчатых фильтров (из различных тканей) и построение графической его зависимости от удельных загрузок. 2. Теоретические положения Ре по з ит о Воздушные фильтры служат для обеспыливания воздуха в системах приточной вентиляции, кондиционирования и воздушного отопления производственных,. служебных и общественных зданий. Очистка воздуха от пыли обязательна в приточных системах, проектируемых для общественных зданий, и в системах, проектируемых для производственных зданий, если содержание пыли в наружном воздухе составляет 30% и более предельно допустимой концентрации (ПДК) пыли в рабочей зоне помещений. Приточный воздух очищается от пыли независимо от ее концентрации при подаче в производственные помещения с повышенными требованиями к чистоте воздуха (радиоэлектронная промышленность, производства точной механики, оптики и т.д.). Важнейшими показателями воздушных фильтров является их эффективность, пылеемкость и аэродинамическоесопротивление. Эффективность очистки η определяется отношением количества уловленной пыли G У Л К количеству пыли поступающей G (3.1) Пылеемкость определяется массовым количеством пыли, задержанной одним м2 поверхности фильтра, при удвоенном его аэродинамическом сопротивлении Рср, Па. Аэродинамическое сопротивление фильтра Рф зависит от воздушной нагрузки L ф, МS/(M2 Ч ). 3. Экспериментальная установка. Методика проведения эксперимента Работа выполняется на лабораторной установке, принципиальная схема которой приведена на рис.3.1. Вентилятором I.воздух по воздуховоду 2 подается в камеру 3, где установлен матерчатый фильтр 4. Измерение расхода воздуха осуществляется в сечении I-.. Сопротивление фильтра определяется по показаниям микроманометра 5. Расход воздуха регулируется заслонкой Ш-3.

7 Потеря давления при проходе воздуха через фильтр равна разности полных давлений в сечениях 2-2 и 3-3. (3.2) где P n2, P n3 – статическое давление в сечениях 2-2 и 3-3; P g2, Р g3 – динамическое давление в cечениях 2-2 и 3-3. Так как площади поперечных, сечений в корпусе фильтра равны и скорости воздуха одинаковы, то Р g2 = Р g3 Следовательно, потеря давления Р между сечениями 2-2 и 3-3 при движении воздуха равна разности статических давлений в этих сечениях, которую можно зафиксировать одним микроманометром, присоединив трубку статического давления в сечении 2 к резервуару, а трубку статического давления в сечении 3 капилляру микроманометра Для того, чтобы вычислить значение потери давления в фильтре, следует учесть потери давления на трение о стенки камеры, где установлен фильтр. ср 2Rl R – потери давления на трение, Па/м. (значение К находим по таблицам, вычислив d экв и определив скорость движения воздуха) Воздушную нагрузку L ф определяют по выражению = Где L расход воздуха, м 3 /ч; F площадь фильтра, м 2. опыт ов g1 P П р асход L Ст ат. давл. 4. Обработка экспериментальных данных Результаты измерений и вычислений заносят в табл.3.1. P c2 Стат а м Па P c3 м/с 3 /ч Па По данным P ф и L необходимо построить аэродинамическую характеристику фильтра для различных расходов воздуха(5 6), которые в работе регулируются шиберов Ш-3 при закрытых Ш-I и Ш-2, и для различных материалов в качестве фильтрующего слоя (марля, бязь, шерстянка) 1 – радиальный вентилятор 2 камера фильтров 3 сменный элемент (300х300) матерчатого фильтра 4 шибер Ш 3 5 микроманометр. давл. Скорост ь движения в сечении камеры, R, Па/ м, l м L ф, м 3 /м 2 ч P Ф, П а Пр имеча н.

8 5. Контрольные вопросы 1. Каковы основные показатели матерчатых фильтров? 2. Где и в каких случаях применяются воздушные фильтры? 3. Какая существует зависимость аэродинамического сопротивления от скорости фильтрации? 4. ПДК в воздухе помещений и в наружном воздухе. 5. Что такое пылеемкость фильтра? 6. Как изменяется аэродинамическое сопротивление фильтра во время его эксплуатации?

9 Лабораторная работа 4 ОПРЕДЕЛЕНИЕ СКОРОСТИ ВИТАНИЯ И СКОРОСТИ ТРОГАНИЯ 1.Цель работы Исследовать опытным путем скорость витания для частицы шарообразной формы и определить скорость трогания частицы, находящейся на стенке горизонтального воздуховода. 2. Теоретические положения Скорость вертикального воздушного потока, при которой тело, находящееся в потоке, падает с равномерной скоростью, или скорость, при которой тело не выпадает из потока и не уносится им ( находится в безразличном равновесии), называется скоростью витания. Скорость частиц различных сыпучих материалов используется для определения действительной скорости транспортирования частиц в системах пневмотранспорта. Любая твердая частица может находится во взвешенном состоянии при условии равенства веса тела силам, возникающим при движении воздуха в направлении снизу вверх и действующим на тело. При этом имеем равенство G=P где G-вес частицы, кг; P- сила, действующая на частицу в направлении снизу вверх. Эта сила может быть определена из выражения (4.1) в в где K 0- опытный коэффициент, учитывающий сумму положительного и отрицательного давлений в долях динамического давления воздушного потока; для частиц шарообразной формы численно равен 0,5. в плотность воздуха, кг/м 3 ; F минимальное сечение частицы по отношению к оси симметрии, м 2 ; скорость движения воздуха, м/с; коэффициент трения; S боковая поверхность частицы, м 2. Таким образом, давление, оказываемое воздухом на тело, слагается из 3-х составляющих: 1) положительного давления, испытываемого сечением частицы, перпендикулярным потоку; 2) отрицательного давления (подсоса), образующегося вследствие отрыва струй, смывающих частицу; 3) трения частицы о воздух. Для шарообразных частиц диаметром d ш, м, и плотностью, кг/м 3, трением их о воздух можно пренебречь( второе слагаемое в правой части выражения (6.1)) как очень малой величиной. Подставив в выражении (6.1) значения G и P, для частиц шарообразной формы будем иметь

10 в (4.2) При К 0 =0,5 и b=1,2 (для воздуха стандартных параметров) скорость витания частицы шарообразной формы будет равна (4.3) т.в.=4,7 Где d ш диаметр шарообразной частицы, м; ш плотность материала, кг/м 3 ; Для определения скорости витания т.в. для шарообразных частиц имеется такая зависимость (4.4) т в Где в – соответственно плотность материала, из которого получена шарообразная частица, и плотность воздуха, кг/м 3 ; в – кинематическая вязкость воздуха, м 2 /с; g ускорение свободного падения, м/с 2/ В задачу лабораторной работы входит определение действительной скорости витания частицы шарообразной формы, имеющей диаметр d ш и плотность ш, кг/м 3, на лабораторной установке и сравнение полученной скорости с теоретически подсчитанной т.в. по выражениям (6.3) и (6.4). Для этой цели предварительно производится вычисление плотности материала и измеряется диаметр частицы (шарика). 3. Экспериментальная установка. Методика проведения опыта Лабораторная установка для определения скорости витания, представленная на рис.4.1, состоит из вентилятора I, воздуховода 2, прозрачной трубы витания 3 с углом раскрытия 3, при котором происходит безотрывное течение воздушного потока, и шиберов 4,5. Для получения равномерного поля скоростей в трубе витания в ее основании расположен наполнительный фильтр, выравнивающий поток по сечению воздуховода. Движение воздуха в трубе витания с различными скоростями при работающем, вентиляторе в закрытом шибере 5 обеспечивается с помощью шибера 4, позволяющего регулировать расход и скорость движения воздуха. Рис. 4.1 в в Из уравнения неразрывности потока следует, что (4.5)

11 н Кн ср н ср ри й БН ТУ F – площадь поперечного сечения прозрачного конуса (трубы витания) на выходе, м2; FH – площадь поперечного сечения трубы витания на уровне высоты витания, м2; ср – средняя скорость воздушного потока в сечении на выходе из трубы витания, м/с; н – средняя скорость воздушного потока на уровне высоты витания Н, равная по величине скорости витания; Кн- коэффициент, учитывающий геометрические размеры конуса. Зависимость площади сечения Fн и коэффициента Кн от высоты витания Н приведена в виде графика на рис.6.3. Рис. 4.2 ср м/с Н мм Кн н м/с dш м ш 3 кг/м Ре по з опы тов ит о Результаты наблюдений, измерений и вычислений сводятся в табл.4.1. т.в. м/с Таблица 4.1. При мечани е На этом стенде исследуется также скорость трогания частиц осевшей в воздуховоде. Эта часть работа выполняется на участке воздуховода, имеющего открывающийся боковой элемент из плексигласа, позволяющий наблюдать момент трогания частицы (шарика и дерева). Работа выполняется в такой последовательности. В воздуховод при неработающем вентиляторе и при закрытых шиберах 4 и 5 через открывающееся отверстие помещается деревянный шарик. После включения вентилятора постепенно открывают шибер 5, увеличивая этим скорость воздушного потока до начала трогания шарика. В этот момент фиксируется величина осевого динамического давления в сечении I, по которой вычисляется средняя скорость движения воздуха в воздуховоде. Полученное значение скорости необходимо сравнить с величиной, определяемой по формуле Клячко, (4.6) р где м – плотность материала, из которого выполнена частица (шарик). Опыты проводятся с шариками из различных материалов.

12 4. Контрольные вопросы 1. Что такое скорость витания? 2. Где используется величина скорости витания частиц измеренного материала? 3. Какие силы действуют на частицу, находящуюся во взвешенном состоянии в воздушном потоке? 4. От каких величин зависит скорость витания шарообразных частиц? 5. Что определяет скорость трогания частицы, выпавшей на стенку воздуховода?

docplayer.ru

Потеря давления в системе Статьи о вентиляции

« Назад

Потеря давления в системе  24.02.2015 08:43

Сопротивление прохождению воздуха в вентиляционной системе, в основном, определяется скоростью движения воздуха в этой системе. С увеличением скорости возрастает и сопротивление. Это явление называется потерей давления. Статическое давление, создаваемое вентилятором, обуславливает движение воздуха в вентиляционной системе, имеющей определенное сопротивление. Чем выше сопротивление такой системы, тем меньше расход воздуха, перемещаемый вентилятором или приточной установкой. Расчет потерь на трение для воздуха в воздуховодах, а также сопротивление сетевого оборудования (фильтр, шумоглушитель, нагреватель, клапан и др.) может быть произведен с помощью соответствующих таблиц и диаграмм, указанных в каталоге. Общее падение давления можно рассчитать, просуммировав показатели сопротивления всех элементов вентиляционной системы.

Рекомендуемая скорость движения воздуха в воздуховодах:

 

Тип		Скоросто воздуха, м/с
Магистральные воздуховоды		6,0 – 8,0
Боковые ответвления		4,0 – 5,0
Распределительные воздуховоды		1,5 – 2,0
Приточные решетки у потолка		1,0 – 3,0
Вытяжные решетки		1,5 – 3,0

Определение скорости движения воздуха в воздуховодах:

V= L / 3600*F (м/сек)

где L – расход воздуха, м³/ч;
F – площадь сечения канала, м².

Рекомендация 1.
Потеря давления в системе воздуховодов может быть снижена за счет увеличения сечения воздуховодов, обеспечивающих относительно одинаковую скорость воздуха во всей системе. На изображении мы видим, как можно обеспечить относительно одинаковую скорость воздуха в сети воздуховодов при минимальной потере давления.

Рекомендация 2.
В системах с большой протяженностью воздуховодов и большим количеством вентиляционных решеток целесообразно размещать вентилятор в середине вентиляционной системы. Такое решение обладает несколькими преимуществами. С одной стороны, снижаются потери давления, а с другой стороны, можно использовать воздуховоды меньшего сечения.

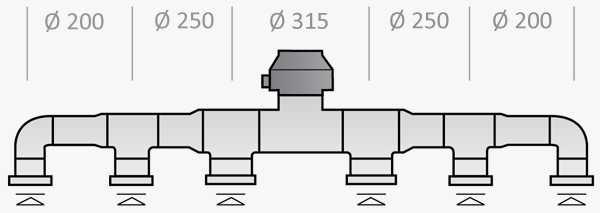
Пример расчета вентиляционной системы:
Расчет необходимо начать с составления эскиза системы с указанием мест расположения воздуховодов, вентиляционных решеток, вентиляторов, а также длин участков воздуховодов между тройниками, затем определить расход воздуха на каждом участке сети.

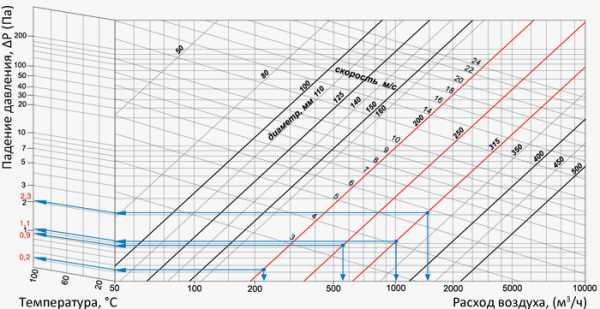
Выясним потери давления для участков 1-6, воспользовавшись графиком потери давления в круглых воздуховодах, определим необходимые диаметры воздуховодов и потерю давления в них при условии, что необходимо обеспечить допустимую скорость движения воздуха.

Участок 1: расход воздуха будет составлять 220 м³/ч. Принимаем диаметр воздуховода равным 200 мм, скорость – 1,95 м/с, потеря давления составит 0,2 Па/м х 15 м = 3 Па (см. диаграмму определение потерь давления в воздуховодах).

Участок 2: повторим те же расчеты, не забыв, что расход воздуха через этот участок уже будет составлять 220+350=570 м³/ч. Принимаем диаметр воздуховода равным 250 мм, скорость – 3,23 м/с. Потеря давления составит 0,9 Па/м х 20 м = 18 Па.

Участок 3: расход воздуха через этот участок будет составлять 1070 м³/ч.
Принимаем диаметр воздуховода равным 315 мм, скорость 3,82 м/с. Потеря давления составит 1,1 Па/м х 20= 22 Па.

Участок 4: расход воздуха через этот участок будет составлять 1570 м³/ч. Принимаем диаметр воздуховода равным 315 мм, скорость – 5,6 м/с. Потеря давления составит 2,3 Па х 20 = 46 Па.

Участок 5: расход воздуха через этот участок будет составлять 1570 м³/ч. Принимаем диаметр воздуховода равным 315 мм, скорость 5,6 м/с. Потеря давления составит 2,3 Па/м х 1= 2,3 Па.

Участок 6: расход воздуха через этот участок будет составлять 1570 м³/ч. Принимаем диаметр воздуховода равным 315 мм, скорость 5,6 м/с. Потеря давления составит 2,3 Па х 10 = 23 Па. Суммарная потеря давления в воздуховодах будет составлять 114,3 Па.

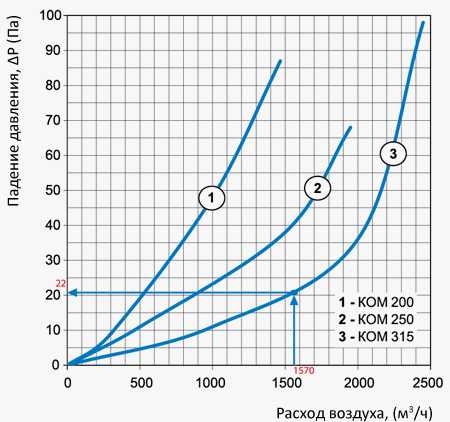
Когда расчет последнего участка завершен, необходимо определить потери давления в сетевых элементах: в шумоглушителе СР 315/900 (16 Па) и в обратном клапане КОМ 315 (22 Па). Также определим потерю давления в отводах к решеткам (сопротивление 4-х отводов в сумме будут составлять 8 Па).

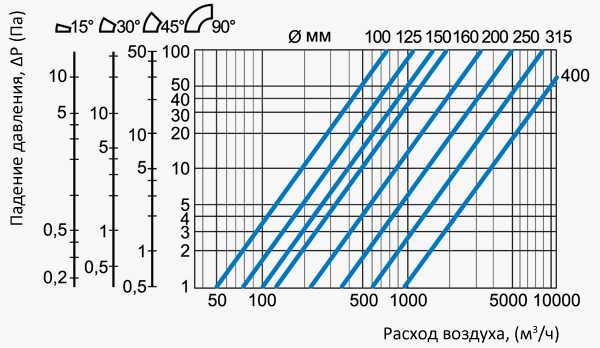
Определение потерь давления на изгибах воздуховодов

График позволяет определить потери давления в отводе, исходя из величины угла изгиба, диаметра и расхода воздуха.

Пример. Определим потерю давления для отвода 90° диаметром 250 мм при расходе воздуха 500 м3/ч. Для этого найдем пересечение вертикальной линии, соответствующей нашему расходу воздуха, с наклонной чертой, характеризующей диаметр 250 мм, и на вертикальной черте слева для отвода в 90° находим величину потери давления, которая составляет 2Па.

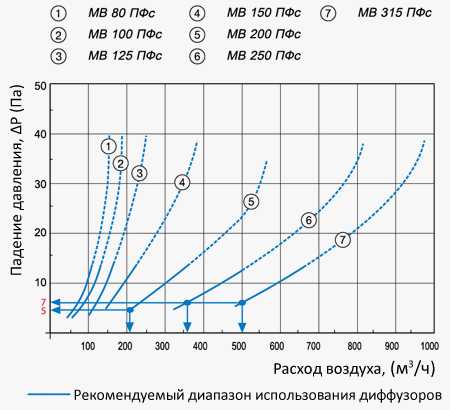
Принимаем к установке потолочные диффузоры серии ПФ, сопротивление которых, согласно графику, будет составлять 26 Па.

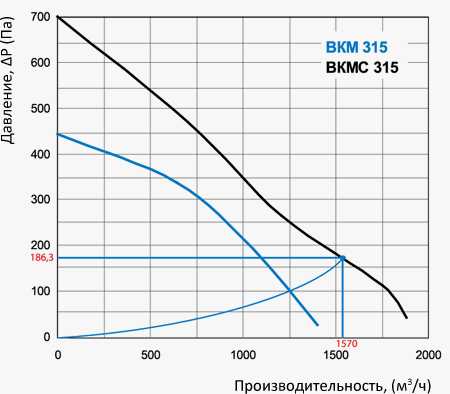
Теперь просуммируем все величины потери давления для прямых участков воздуховодов, сетевых элементов, отводов и решеток. Искомая величина 186,3 Па.

Мы рассчитали систему и определили, что нам нужен вентилятор, удаляющий 1570 м3/ч воздуха при сопротивлении сети 186,3 Па. Учитывая требуемые для работы системы характеристики нас устроит вентилятор требуемые для работы системы характеристики нас устроит вентилятор ВЕНТС ВКМС 315.

Определение потерь давления в воздуховодах.

Определение потерь давления в обратном клапане.

Подбор необходимого вентилятора.

Определение потерь давления в шумоглушителях.

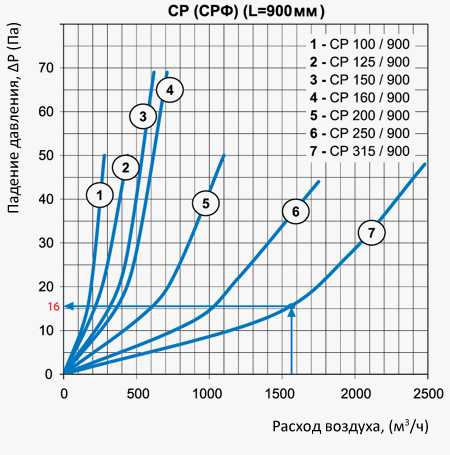
Определение потерь давления на изгибах воздухуводов.

Определение потерь давления в диффузорах.

cyclonespb.ru

Лекция №4. Теоретические основы вентиляции

15

1. Расчет воздуховодов приточных и вытяжных систем механической и естественной вентиляции

Аэродинамический расчет воздуховодов обычно сводится к определению размеров их поперечного сечения, а также потерь давления на отдельных участках и в системе в целом. Можно определять расходы воздуха при заданных размерах воздуховодов и известном перепаде давления в системе.

При аэродинамическом расчете воздуховодов систем вентиляции обычно пренебрегают сжимаемостью перемещающегося воздуха и пользуются значениями избыточных давлений, принимая за условный нуль атмосферное давление.

При движении воздуха по воздуховоду в любом поперечном сечении потока различают три вида давления: статическое, динамическое и полное.

Статическое давление определяет потенциальную энергию 1 м³ воздуха в рассматриваемом сечении (р_ст равно давлению на стенки воздуховода).

Динамическое давление – это кинетическая энергия потока, отнесенная к 1 м³ воздуха, определяется по формуле:

(1)

где – плотность воздуха, кг/м³; – скорость движения воздуха в сечении, м/с.

Полное давление равно сумме статического и динамического давлений.

(2)

Традиционно при расчете сети воздуховодов применяется термин “потери давления” (“потери энергии потока”).

Потери давления (полные) в системе вентиляции складываются из потерь на трение и потерь в местных сопротивлениях (см.: Отопление и вентиляция, ч. 2.1 “Вентиляция” под ред. В.Н. Богословского, М., 1976).

Потери давления на трение определяются по формуле Дарси:

(3)

где – коэффициент сопротивления трению, который рассчитывается по универсальной формуле А.Д. Альтшуля:

(4)

где – критерий Рейнольдса; К – высота выступов шероховатости (абсолютная шероховатость).При инженерных расчетах потери давления на трение , Па (кг/м²), в воздуховоде длиной /, м, определяются по выражению

(5)

где – потери давления на 1 мм длины воздуховода, Па/м [кг/(м² * м)].

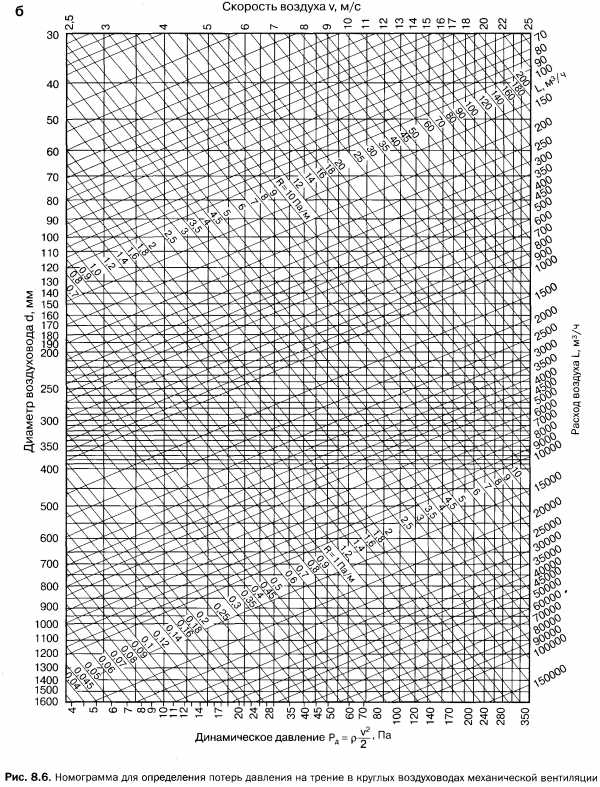
Для определения R составлены таблицы и номограммы. Номограммы (рис. 1 и 2) построены для условий: форма сечения воздуховода круг диаметром, давление воздуха 98 кПа (1 ат), температура 20°С, шероховатость= 0,1 мм.

Для расчета воздуховодов и каналов прямоугольного сечения пользуются таблицами и номограммами для круглых воздуховодов, вводя при этом эквивалентный диаметр прямоугольного воздуховода, при котором потери давления на трение в круглом и прямоугольном ~ воздуховодахравны.

В практике проектирования получили распространение три вида эквивалентных диаметров:

■ по скорости

при равенстве скоростей

■ по расходу

при равенстве расходов

■ по площади поперечного сечения

при равенстве площадей сечения

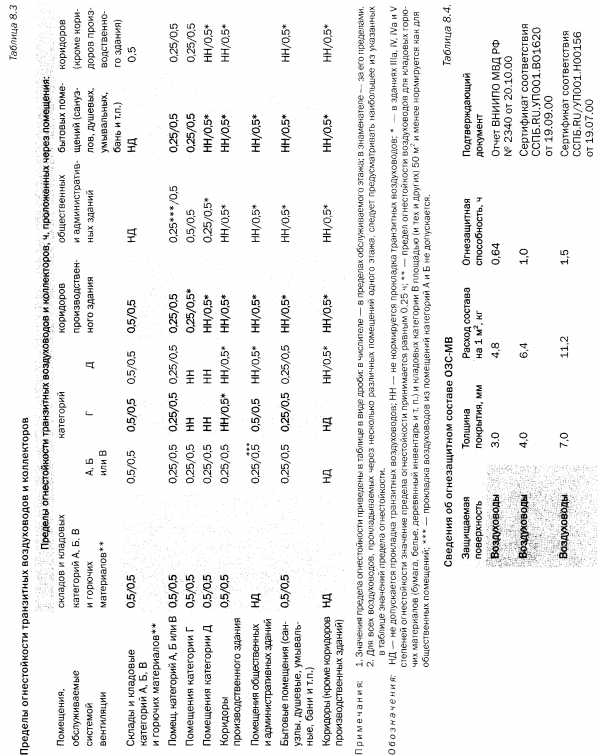
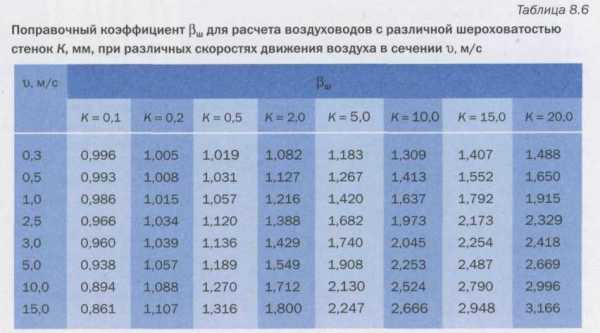
При расчете воздуховодов с шероховатостью стенок, отличающейся от предусмотренной в таблицах или в номограммах (К = ОД мм), дают поправку к табличному значению удельных потерь давления на трение:

(6)

где – табличное значение удельных потерь давления на трение; – коэффициент учета шероховатости стенок (табл. 8.6).

Потери давления в местных сопротивлениях. В местах поворота воздуховода, при делении и слиянии потоков в тройниках, при изменении размеров воздуховода (расширение – в диффузоре, сужение – в конфузоре), при входе в воздуховод или в канал и выходе из него, а также в местах установки регулирующих устройств (дросселей, шиберов, диафрагм) наблюдается падение давления в потоке перемещающегося воздуха. В указанных местах происходит перестройка полей скоростей воздуха в воздуховоде и образование вихревых зон у стенок, что сопровождается потерей энергии потока. Выравнивание потока происходит на некотором расстоянии после прохождения этих мест. Условно, для удобства проведения аэродинамического расчета, потери давления в местных сопротивлениях считают сосредоточенными.

Потери давления в местном сопротивлении определяются по формуле

(7)

где – коэффициент местного сопротивления (обычно, в отдельных случаях имеет место отрицательное значение, при расчетах следует учитывать знак).

Коэффициентотносится к наибольшей скорости в суженном сечении участка или скорости в сечении участка с меньшим расходом (в тройнике). В таблицах коэффициентов местных сопротивлений указано, к какой скорости относится.

Потери давления в местных сопротивлениях участка, z, рассчитываются по формуле

(8)

где – сумма коэффициентов местных сопротивлений на участке.

Общие потери давления на участке воздуховода длиной, м, при наличии местных сопротивлений:

(9)

где – потери давления на 1 м длины воздуховода; – потери давления в местных сопротивлениях участка.

studfiles.net

Потеря давления на преодоление сопротивлений трения – Водяное отопление – Отопление

Потеря давления на преодоление сопротивлений трения, отнесенная к 1 м длины трубы, называется гидравлическим уклоном i или удельной потерей давления R.

Первое из этих определений общепринято при расчете систем водоснабжения, второе — при расчете трубопроводов систем отопления, вентиляции и газоснабжения.

Потеря давления на трение определяется по формуле Дарси — Вейсбаха

Rl=λl/d*ω²ϒ/2g, или Rl= λl/d H_д,

где R — удельная потеря давления, отнесенная к 1 м длины трубы, в кг/м²;

l — длина участка трубы с постоянным расходом в м;

λ — безразмерный коэффициент трения, величина которого зависит от значения числа Рейнольдса (т. е. от характера движения потока), диаметра трубы, степени шероховатости ее стенок и физических свойств движущейся среды;

d — внутренний диаметр трубы в м;

ω — скорость движения среды в трубе в м/сек;

g — ускорение силы тяжести в м/сек²;

γ — удельный вес среды в кг/м³, для воды γ = 970 при t = 82,5°; для пара γ = 0,7 при давлении 0,2 кг/см²; для стандартного воздуха γ = 1,2 при t = 20°; для природного газа γ = 0,73 — 0,76 при t = 20° и барометрическом давлении 760 мм рт. ст.;

H_д — динамическое (скоростное) давление, которым обладает движущаяся среда.

Потеря давления на местные сопротивления определяется по формуле

z = ζ * ω²ϒ/2g, или z = ζH_д

где ζ — безразмерный коэффициент, характеризующий данное местное сопротивление.

Местные сопротивления многочисленны по наименованиям и различны по значениям коэффициентов, поэтому здесь приводятся только некоторые из них:

радиатор	2,0
тройник проходной	1,0
тройник «ответвление» (или поворот)	1,5
крестовина проходная	2,0
кран пробочный (при d=15 и 20 мм)	2 — 4
винтель с прямым шпинделем (при d= 15 и 20 мм)	10 — 16

Потери давления на преодоление местных сопротивлений и сопротивлений трения примерно одинаковы при насосном водяном отоплении и паровом отоплении низкого давления. В воздуховодах местные сопротивления превышают в несколько раз сопротивления трения.

Определение удельной потери давления производится по специальным расчетным таблицам или номограммам.

На рисунке ниже приведены такие номограммы для расчета водогазопроводных труб систем водяного и парового отопления и труб из кровельной стали (воздуховодов) систем воздушного отопления и вентиляции.

---

Номограммы для расчета труб

а — водяного отопления; б — парового отопления; в — воздушного отопления и вентиляции.

---

Эти три номограммы построены по формуле Дарси — Вейсбаха, поэтому одинаковы по своему начертанию. Так как они здесь предназначены только для учебных целей, то охватывают незначительный расчетный диапазон.

Каждой такой номограммой связаны четыре расчетных параметра:

• расход, выраженный количеством воды (а кг/ч)^* для водяного отопления, количеством тепла (в ккал/ч) для парового отопления, количеством воздуха (в м/ч) для воздушного отопления и вентиляции;
• внутренний диаметр трубы или воздуховода;
• удельная потеря давления, отнесенная к 1 м длины трубы, в кг/м²;
• скорость движения среды (воды, пара, воздуха) в трубе в м/сек.

На оси абсцисс дан масштаб расходов, на оси ординат — масштаб удельной потери давления. На поле номограммы нанесены перекрещивающиеся линии скоростей и диаметров. Зная два любых расчетных параметра, одним из которых обычно является расход, можно определить два оставшихся.

Максимальные скорости движения воды в трубах системы насосного отопления принимаются от 0,5 м/сек (при диаметре в 15 мм) до 1,5 м/сек (диаметр 50 мм и более).

Для труб тех же диаметров наибольшие скорости движения пара низкого давления составляют 14 и 30 м/сек. В воздуховодах скорость воздуха не превышает 10 — 12 м/сек.

Энергия, расходуемая на преодоление гидравлических сопротивлений циркуляционного кольца системы водяного отопления, как и магистрали систем парового или воздушного отопления и вентиляции, сообщается:

воде — за счет гравитационных сил или действием центробежного насоса;

пару — за счет давления, приобретаемого им в котле;

воздуху — за счет сил гравитации или работы вентилятора в размере Н = Σ(Rl+z)1-n кг/м², где n — количество участков циркуляционного кольца или магистрали.

При механическом побуждении движения в водяной системе отопления значение величины Н определяется технико-экономическими соображениями или задается нормами. Так, в частности, для жилых домов Н = 1000/1200 кг/м² при питании системы от тепловой сети.

^*С незначительной погрешностью можно считать в л/ч.

«Санитарно-технические устройства зданий»,
В.В.Конокотин

Основными расчетами систем водяного отопления, кроме подсчета теплопотерь, определяются площади нагревательных приборов и диаметров труб, питающих эти приборы. Площадь нагревательных приборов находится из выражения, общего для водяного и парового отопления:Fпр kпр (tпр-tв) = Qпр, где Fпр — площадь прибора или группы приборов (устанавливаемых в одном помещении) в м2; kпр — коэффициент теплопередачи прибора в ккал/м2*ч*°С,…

Понятие экм упрощает теплотехнические расчеты, связанные с определением площади нагревательных приборов. Пересчет из экм в размеры конкретного нагревательного прибора не встречает затруднений. Пользуясь экм, легко дать сравнительную экономическую характеристику приборам различных типов, так как чем меньше будет вес прибора при его теплоотдаче, равной 435 ккал/ч (теплоотдача 1 экм), тем, следовательно, он окажется дешевле (меньший расход…

Случаи применения гравитационных систем (за исключением квартирного отопления) редки. Современные системы водяного отопления осуществляются, как правило, с искусственным побуждением циркуляции воды за счет работы центробежного насоса с электроприводом, установленного в помещении котельной. Высокое давление, создаваемое насосом (3000 — 5000 кг/м2), обеспечивает большую скорость передвижения воды по трубам относительно малого диаметра (в сравнении с гравитационными системами),…

При устройстве фундамента из рваного камня или из бетонных блоков балки располагаются непосредственно под кирпичной кладкой. Заделка проема производится пенобетонным боем на цементном растворе с последующей штукатуркой. В зданиях располагаются узлы управления (тепловой центр), для размещения которых отводится помещение площадью 12 — 15 м2 в техническом подполье или в подвальном этаже, используемом и для прокладки…

В зависимости от положения горячей магистрали системы подразделяются на системы с верхней разводкой, нижней и смешанной или поэтажной (на рисунке ниже положение – А и Б, Г и В). Смотрите рисунок и описание к нему ниже – Принципиальные схемы систем водяного отопления А — система с верхней разводкой и тупиковым движением воды; Б — система…

www.ktovdome.ru

Определение естественного давления и расчёт воздуховодов — КиберПедия

 

Для нормальной работы системы естественной вентиляции необходимо, чтобы было сохранено равенство

, (6.2)

где R – удельная потеря давления на трение, Па/м; l – длина воздуховодов (каналов), м; Rl – потеря давления на трение расчётной ветви, Па; Z – потеря давления на местные сопротивления, Па; – располагаемое давление, Па; a – коэффициент запаса, равный 1,1…1,15, b – поправочный коэффициент на шероховатость поверхности.

Расчёту воздуховодов (каналов) должна предшествовать следующая расчётно-графическая работа.

1. Определение воздухообменов для каждого помещения по кратностям (согласно СНиП соответствующего здания).

2. Компоновка систем вентиляции. В одну систему объединяют только одноименные или близкие по назначению помещения. Системы вентиляции квартир, общежитий и гостиниц не совмещают с системами вентиляции детских садов и яслей, торговых и других учреждений, находящихся в том же здании. Санитарные узлы во всех случаях обслуживаются самостоятельными системами и при пяти унитазах и более оборудуются механическими побудителями. В детских садах и яслях рекомендуется устраивать вытяжные системы естественной вентиляции, самостоятельные для каждой группы детей, объединяя помещения с учётом их назначения. В курительных комнатах, как правило, осуществляется механическая вентиляция. Вытяжку из комнат жилого дома сокнами, выходящими на одну сторону, рекомендуется объединять в одну систему.

3. Графическое изображение на планах этажей и чердака элементов системы (каналов и воздуховодов, вытяжных отверстии и жалюзийных решёток, вытяжных шахт). Против вытяжных отверстий помещений указывается количество воздуха, удаляемого по каналу. Транзитные каналы, обслуживающие помещения нижних этажей, рекомендуется обозначать римскими цифрами (I, II, III и т.д.). Все системы вентиляции должны быть пронумерованы.

4. Вычерчивание аксонометрических схем в линиях, или, что лучше, с изображением внешних очертаний всех элементов системы (рис. 6.4). На схемах в кружке у выносной черты проставляется номер участки, над чертой указывается нагрузка участка, м³/ч, а под чертой – длина участка, м. Аэродинамический расчёт воздуховодов (каналов) выполняют по таблице или номограммам, составленным для стальных, воздуховодов круглого сечения при r_в = l,205 кг/м³,
t_в = 20 °С. В них взаимосвязаны величины L, R, v, h_vи d.

Аэродинамический расчёт воздуховодов системы вентиляции сводится:

– к определению размеров воздуховодов, каналов отдельных участков сети, обеспечивающих перемещение требуемого количества воздуха;

– к определению суммарного сопротивления, возникающего при движении воздуха в магистральной сети, для определения в дальнейшем расчётного давления, создаваемого вентилятором;

– к возможной увязке потерь давления на отдельных участках сети воздуховодов.

Наименьшая скорость движения воздуха в системах с механическим побуждением, с учётом акустических требований, принимается на участках перед обслуживаемыми помещениями (3 – 5 м/с), наибольшая – в магистральных воздуховодах перед вентиляционными установками (до 7 – 9 м/с). В системах естественной вентиляции скорость движения воздуха, как правило, не превышает 0,9 –1,1 м/с.

Аэродинамический расчёт ведётся преимущественно по методу удельных потерь. Расчётная потеря давления в наиболее протяженной и нагруженной магистральной сети воздуховодов Δр^рпредставляет сумму потерь давления на каждом расчётном участке магистрали

Δр^р = Σ (Δр_тр + Δр_мс) = Σ [R_трl β_ш + Σξ (v²ρ/2)],Па (кг/м²)(6.3)

где Δр_три Δр_мспотери давления, Па (кг/м²), на расчётном участке соответственно по длине l, м, и в местных сопротивлениях; R_тр– удельная потеря на трение, Па/м (кг/м²×м), определяемая по таблицам, номограммам [10] или расчётным путём;
β_ш– коэффициент, учитывающий шероховатость внутренней поверхности воздуховода, канала; Σξ – сумма коэффициентов местных сопротивлений в долях динамического давления, определяемых экспериментально и принимаемых по таблицам в справочной литературе; v – скорость движения воздуха в воздуховоде, м/с; ρ – плотность воздуха, кг/м³.

Таблицы и номограммы [10] для определения R_трсоставлены для круглых воздуховодов. Поэтому при применении воздуховодов прямоугольной формы пользуются понятием «эквивалентный диаметр» прямоугольного воздуховода, при котором потери давления на трение R_трв круглом и прямоугольном воздуховодах равны.

Номограмма для расчёта стальных воздуховодов круглого селения системы естественной вентиляции показана на рис. 6.5. Чтобы воспользоваться номограммой для расчёта воздуховода прямоугольного сечения, необходимо предварительно определить соответствующую величину равновеликого (эквивалентного) диаметра, т. е. такого диаметра круглого воздуховода, при котором для той же скорости, движения воздуха, как и в прямоугольном воздуховоде, удельные потери давления на трение были бы равны. Обычно эквивалентный диаметр d_э, м, определяют по формуле, исходя из равенства скоростей в воздуховодах

, (6.4)

где a, b – размеры сторон прямоугольного воздуховода, м.

Эквивалентные по трению диаметры для кирпичных каналов приведены в табл. 6.1.

 

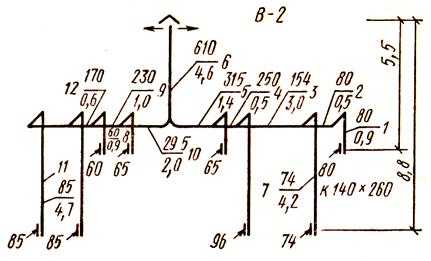
Рис. 6.4. Схема системы вытяжной вентиляции

 

 

Таблица 6.1 – Эквивалентные по трению диаметры для кирпичных каналов [11]

Размер в кирпичах	Площадь, м2	,мм
1/2´1/2	0,02
1/2´1	0,038
1´1	0,073
1´1	0,11
1´2	0,14
2´2	0,28

Примечание. Для каналов квадратного сечения эквивалентный по трению диаметр равен стороне квадратного канала а.

 

Если воздуховоды имеют шероховатую поверхность, то коэффициент трения для них, а следовательно, и удельная потеря давления на трение будут соответственно больше, чем указано в таблице или номограмме для стальных воздуховодов.

Поправочные коэффициеты на шероховатость поверхности воздуховода приведены в табл. 6.2.

Методика расчёта воздуховодов (каналов) систем естественной вентиляции может быть представлена в следующем виде [11].

1. При заданных объёмах воздуха, подлежащего перемещению по каждому участку каналов, принимают скорость его движения.

2. По объёму воздуха и принятой скорости определяют предварительно площадь сечения каналов. Потери давления на трение и местные сопротивления для таких сечений каналов выявляют по таблицам или номограммам.

 

Таблица 6.2 – Значение коэффициентов шероховатости b [11]

Скорость движения воздуха, м/с	При материале трубопровода
шлакогипсе	шлакобетоне	кирпиче	штукатурке по сетке
0,4	1,08	1,11	1,25	1,48
0,8	1,13	1,19	1,4	1,69
1,2	1,18	1,25	1,5	1,84
1,6	1,22	1,31	1,58	1,95
	1,25	1,35	1,65	2,04
2,4	1,28	1,38	1,7	2,11
	1,32	1,43	1,77	2,2
	1,37	1,49	1,86	2,32
	1,41	1,54	1,93	2,41
	1,44	1,58	1,98	2,48
	1,47	1,61	2,03	2,54
	1,49	1,64	2,06	2,58

 

3. Сравнивают полученные суммарные сопротивления с располагае­мым давлением. Если эти величины совпадают, то предварительно полученные площади сечения каналов могут быть приняты как окончательные. Если же потери давления оказались меньше или больше располагаемого давления, то площадь сечения каналов следует увеличить или, наоборот, уменьшить, т.е. поступать так же, как при расчёте трубопровода системы отопления.

При предварительном определении площади сечений каналов систем естественной вентиляции можно задаваться следующими скоростями движения воздуха: в вертикальных каналах верхнего этажа v = 0,5 – 0,6 м/с, из каждого нижерасположенного этажа на 0,1 м/с больше, чем из предыдущего, но не выше 1 м/с; в сборных воздуховодах v ³1 м/с и в вытяжной шахте v = 1 – 1,5 м/с.

Если при расчёте воздуховодов задана площадь сечения каналов и известен часовой расход воздуха, то скорость v, м/с, определяется по формуле

, (6.4)

где f – площадь сечения канала или воздуховода, м²; L – объём вентиляционного воздуха, м³/ч.

Потери давления на местные сопротивления

, (6.5)

где – сумма коэффициентов местных сопротивлений; – динамическое давление, Па.

Динамическое давление определяется по дополнительной шкале номограммы для расчёта воздуховодов (приведена с правой стороны номограммы).

Местные сопротивления в системе вентиляции во многих случаях существенно зависят от соотношений размеров фасонных частей и других вентиляционных элементов, а в тройниках-крестовинах от соотношений соединяемых или делимых потоков.

Пример 6.1. Рассчитать воздуховоды системы естественной вытяжной вентиляции, обслуживающей кабинеты двухэтажного здания поликлиники [11]. Аксонометрическая схема системы вентиляции с указанием объёма воздуха, проходящего по каждому участку, длин и номеров участков показана на рис. 6.3.

Воздух удаляется из верхней зоны помещений на высоте 0,5 м от потолка. Высота этажей, включая толщину перекрытия, 3,3 м. Высота чердака под коньком крыши 3,6 м.

Порядок расчёта. Температура наружного воздуха для расчёта вытяжной системы естественной вентиляции принимается равной + 5 °C (r₅ = 1,27 кг/м³). Внутренняя температура воздуха во врачебных кабинетах, согласно СНиП должна быть 20 °C (r₂₀ = 1,205 кг/м³). При высоте чердака 3,6 м принимаем высоту вытяжной шахты, исчисляя её от оси горизонтальноговоздуховода до устья шахты, 4,6 м.

Располагаемое естественное давление в системе вентиляции для помещений второго этажа согласно формуле (6.1), равно

Па,

а для помещений первого этажа

Па.

Расчёт воздуховодов начинаем с наиболее неблагоприятно расположенного канала, для которого возможная удельная потеря давления имеет наименьшее значение.

Из схемы системы вентиляции видно, что таким будет канал второго этажа правой ветки, обозначенный № 1 (см. рис. 6.3).

Действительно, возможная удельная потеря давления для участков 1, 2, 3, 4, 5 и 6 при общей длине их

м

будет

Па,

а для участков 7, 3, 4, 5 и 6 при общей длине их

м

Па.

Приступаем к расчётам участков 1, 2, 3, 4, 5 и 6, для которых удельное давление получилось меньше.

 

 

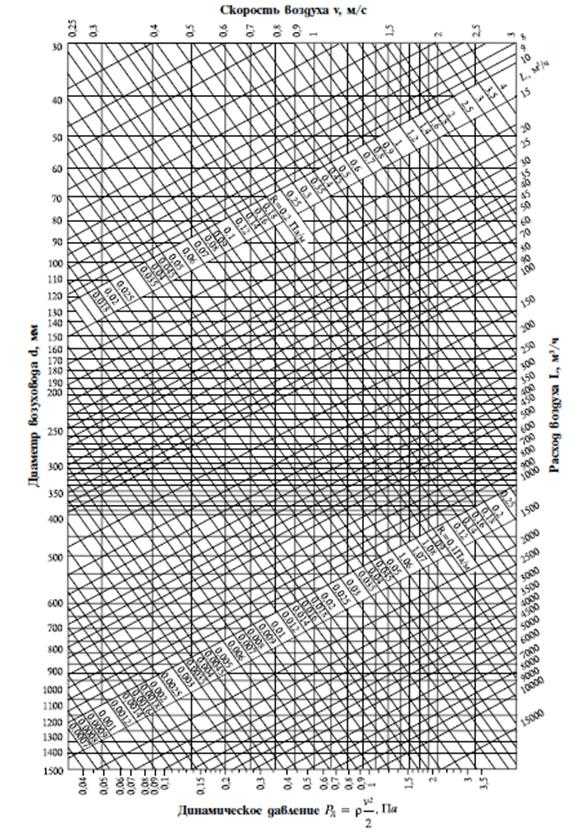
Рис. 6.5. Номограмма для расчёта круглых стальных воздуховодов [10]

Участок 1. Для определения площади сечения канала участка 1 задаёмся скоростью движения воздуха в нём 0,6 м/с. При этой скорости и количестве удаляемого воздуха по каналу L = 80 м³/ч площадь сечения канала f, м², по формуле должна быть

м².

Принимаем для участка 1 кирпичный канал кирпич. Площадь сечения канала с учётом швов f = 0,038 м². При этой площади сечения факти­чески скорость движения воздуха v, м/с,

м/с.

Так как этот канал прямоугольного сечения, для определения потери давления на трение необходимо установить по табл. 6.1 эквивалентный диаметр. Он будет равен180 мм.

Пользуясь приведённой выше номограммой (см. рис. 6.4), находим, что при скорости движения воздуха 0,58 м/с в воздуховоде диаметром 180 мм потеря давления на трение на 1 м воздуховода равна 0,04 Па, а на всем участке 1 длиной 0,9 м с учётом коэффициента шероховатости (см. табл. 6.2).

Па.

Далее по прил. Ж находим сумму коэффициентов местных сопротивлений участка:

вход в жалюзийную решётку с поворотом потока x = 2;

два прямоугольных колена вверхнейчасти канала

.

Сумма коэффициентов местных сопротивлений для участка 1

.

Динамическое давление h_vнаходим по скорости движения воздуха
0,58 м/с на номограмме внизу; оно равно 0,19 Па.

Потерю давления на местные сопротивления Z участка 1 определяем, умножая величину на h_v

Па.

Общая потеря давления на участке 1 составляет

Па.

Участок 2. На участках 1 и 2,количество движущегося воздуха одинаково (80 м³/ч), но площади сечения кирпичного канала и горизонтального гипсошлакового короба разные.

Горизонтальный гипсошлаковый короб принимаем размером 220´220 мм
(f = 0,048 м²). Эквивалентный диаметр d_э = 220 мм. Скорость движения воздуха научастке

м/с,

что при длине участка 0,5 м можно допустить, учитывая, что шлакогипсовые двойные короба не изготовляются размером меньшим, чем 220´220 мм.

При d_э = 220 мм и v = 0,47 м/с потеря давления на трение на этомучастке с учётом коэффициента шероховатости будет

Па.

На участке 2 имеется лишь одно местное сопротивление через тройник. По прил. Ж находим, что сопротивление тройника на проход z = 1,15.

Динамическое давление h_vпри v = 0,47 м/с равно 0,13 Па. Потеря давления на местные сопротивления

Па.

Общая потеря давления на участке 2

Па.

Участок 3. Согласно данным, приведённым выше, задаёмся скоростью движения воздуха на участке 3 в 1 м/с. Тогда при количестве удаляемого воздуха L = 154 м³/ч по участку 3 площадь сечении короба должна быть равна

м².

Принимаем короб из гипсошлаковых плит размером 220´220 мм, эквивалентный диаметр d_э = 220 мм; фактическая скорость движения воздуха ввоздуховоде будет v = 0,89 м/с. При этих условиях потеря давления на трение на участке равна

Па.

На участке 3 имеется лишь одно местное сопротивление при проходе через тройник и следующий участок 4.

По прил. Ж интерполяцией находим, что коэффициент местного сопротивления тройника z = 0,65; динамическое давление при v = 0,89 м/с равно 0,49 Па.

Потеря давления на местные сопротивления участка 3

Па.

Общая потеря давления на участке 3 составляет

Па.

Участок 4. На участке 4 размер воздуховода принимаем 300´300 мм. При количестве удаляемого воздуха L = 250 м³/ч и площади сечения воздуховода
f = 0,09 м² скорость равна

м/с.

При d_э = 300 мм и v = 0,77 м/с потери давления на трение на участке 4

Па.

На участке 4 имеется тройник на проходе, и коэффициент местного сопротивления z = 0,4.

Динамическое давление при скорости удаляемого воздуха 0,77 м/с равно 0,37 Па. Потеря давления на местное сопротивление участка 4 (втройнике)

Па.

Общая потеря давления на участке 4

Па.

Участок 5. На участке 5 размеры короба не изменяем, и скорость воздуха на этом участке

м/с.

При v = 0,97 м/с и d_э = 300 мм потеря давления на трение составляет

Па.

На участке 5 имеется тройник на всасывание сz = 0,8. Динамическое давление при скорости движения воздуха 0,97 м/с равно 0,57 Па.

Потеря давления на местное сопротивление на участке 5

Па.

Общая потеря давления на участке 5

Па.

Участок 6. На участке 6 размер короба увеличиваем до 400´400 мм, так как суммарное количество воздуха, удаляемого системой вентиляции, равно
610 м³/ч.

Фактическая скорость движения воздуха в шахте

м/с.

При v = 1,00 м/с и d_э = 400 мм потеря давления на участке составит

Па.

На участке 6 имеется два вида местного сопротивления – утеплённый клапан и деревянная утеплённаяшахта с зонтом. Коэффициент местного сопротивления z утеплённого клапана 0,1, а вытяжной шахты с зонтом – 1,3.

Динамическое давление при скорости движения воздуха 1,06 м/с
h_v = 0,66 Па.

Потеря давления на преодоление местных сопротивлений

Па.

Общая потеря давления на участке 6

Па.

Суммарная потеря давления в ветке

Па.

При располагаемом давлении в системе для второго этажа Dр₂=3,53 Па.

Дальнейший подбор площади сечений каналов и короба должен быть произведён с увязкой потерь давления. Так, например, для участка 7 канала, обслуживающего кабинет первого этажа, необходимо из общего давления Dр₁=5,59 Па вычесть потерю давления на участках 3, 4, 5, 6,которые мы уже рассчитали.

В результате будем иметь

Па.

Потеря давления на участке 7 составляет 0,67 Па (табл. 7.3), т. е. избыточное давление на этом участке

Па.

Потери давления на участках 8, 9 и 10 должны быть равны располагаемому давлению для каналов второго этажа за вычетом потери давления в вытяжной шахте, которая уже определена (см. участок 6).Потери давления на участках 11 и 12 должны быть равны располагаемому давлению для каналов первого этажа, уменьшенному на суммарную потерю участков 6, 9 и 10. Сечение канала 13 подбирается по располагаемому давлению для первого этажа за вычетом суммарной потери давления на участках 12, 10, 9 и 6. В процессе расчёта воздуховодов системы вентиляции заполняются специальные таблицы (табл. 6.3 и 6.4).

 

Таблица 6.3 – Результаты расчёта воздуховодов системы естественной вытяжной вентиляции

№ участка	L, м3/ч	l, м	a´b, мм	dэ, м	f, м2	v, м/c	R, Па/м	Rlb, Па	hv, Па	Sz	Z, Па	Rlb+Z, Па
		0,9	140´270		0,038	0,58	0,04	0,047	0,19	4,52	0,86	0,91
		0,5	220´220		0,048	0,47	0,026	0,014	0,13	0,15	0,15	0,16
			220´220		0,048	0,89	0,065	0,22	0,49	0,65	0,32	0,54
		0,5	300´300		0,09	0,77	0,034	0,020	0,37	0,4	0,15	0,17
		1,4	300´300		0,09	0,97	0,52	0,084	0,57	0,8	0,46	0,54
		4,6	400´400		0,16	1,06	0,043	0,023	0,66	1,4
		4,2	140´270		0,038	0,54	0,035	0,15	0,18	2,88	0,52	0,67

 

Таблица 6.4 – Значение коэффициента местного сопротивления z [11]

№ участка	Местное сопротивление	z	Sz
	Вход в жалюзийную решётку с поворотом потока Колено прямоугольное 2´1,26	2,52	4,52 4,52
	Тройник на проход	1,15	1,15
	То же	0,65	0,65
	Тройник: на проход на всасывание	0,4 0,8	0,4 0,8
	Клапан утеплённый	0,1	1,4
	Шахта с зонтом	1,3	1,4

 

 

cyberpedia.su